|
Size: 629
Comment:
|
Size: 2661
Comment: added link to complex analysis
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 3: | Line 3: |
| Post code that demonstrates the use of the interact command in Sage here. It should be easy for people to just scroll through and paste examples out of here into their own sage notebooks. | This is a collection of pages demonstrating the use of the **interact** command in Sage. It should be easy to just scroll through and copy/paste examples into Sage notebooks. If you have suggestions on how to improve interact, add them [[interact/Suggestions|here]] or email the sage-support mailing list. Of course, your own examples are also welcome! |
| Line 5: | Line 8: |
| We'll likely restructure and reorganize this once we have some nontrivial content and get a sense of how it is laid out. | Documentation links: |
| Line 7: | Line 10: |
| == Graphics == | * [[http://doc.sagemath.org/html/en/reference/repl/sage/repl/ipython_kernel/interact.html| interacts in the Jupyter notebook]] (see this page and the two following ones) * [[https://github.com/sagemath/sagenb/blob/master/sagenb/notebook/interact.py|interacts in the legacy SageNB notebook]] (many helpful examples) * [[https://github.com/sagemath/sagecell/blob/master/interact_compatibility.py|Sage Cell Server implementation]] * [[https://github.com/sagemathinc/cocalc/blob/master/src/smc_sagews/smc_sagews/sage_salvus.py#L348|CoCalc Sage worksheet implementation]] |
| Line 9: | Line 15: |
| == Calculus == | Examples: |
| Line 11: | Line 17: |
| == Number Theory == | * [[interact/algebra|Algebra]] * [[interact/bio|Bioinformatics]] * [[interact/calculus|Calculus]] * [[interact/complex|Complex Analysis]] * [[interact/cryptography|Cryptography]] * [[interact/diffeq|Differential Equations]] * [[interact/graphics|Drawing Graphics]] * [[interact/dynsys|Dynamical Systems]] * [[interact/fractal|Fractals]] * [[interact/games|Games and Diversions]] * [[interact/geometry|Geometry]] * [[interact/graph_theory|Graph Theory]] * [[interact/linear_algebra|Linear Algebra]] * [[interact/Loop Quantum Gravity|Loop Quantum Gravity]] * [[interact/misc|Miscellaneous]] * [[interact/number_theory|Number Theory]] * [[interact/stats|Statistics/Probability]] * [[interact/topology|Topology]] * [[interact/web|Web Applications]] |
| Line 13: | Line 37: |
| {{{ html('<h1>Cuspidal Subgroups of Modular Jacobians J0(N)</h1>') |
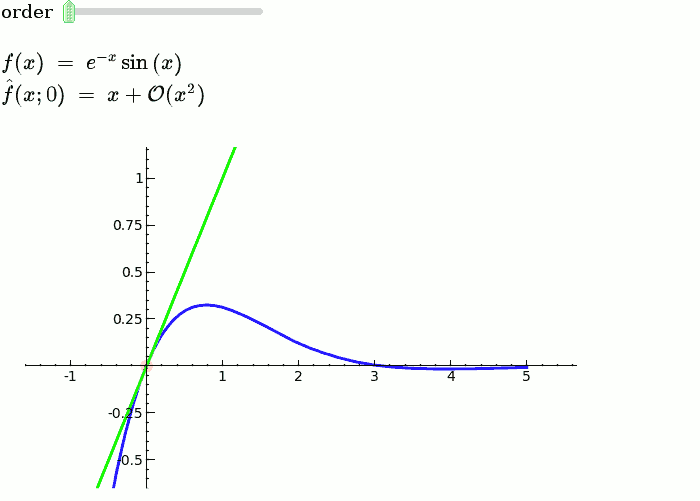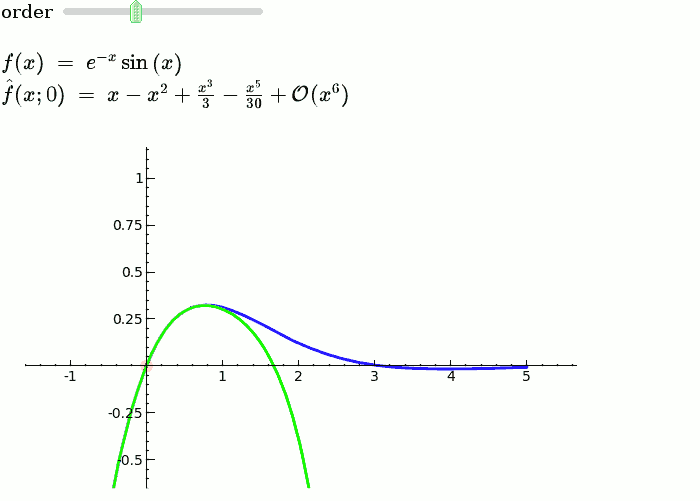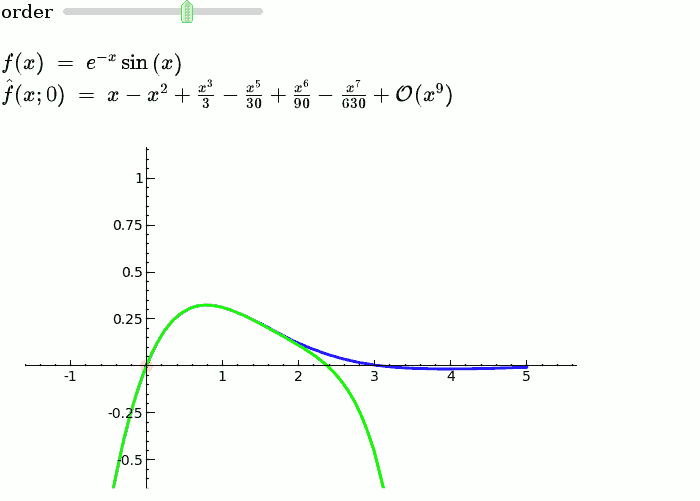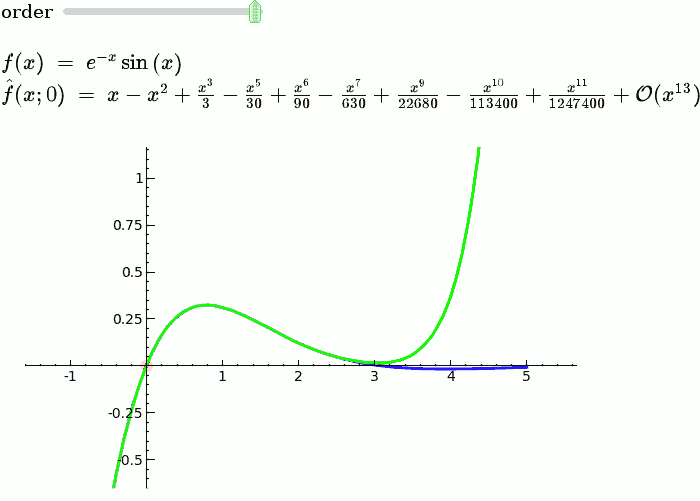
== Explanatory example: Taylor Series == This is the code and a mockup animation of the interact command. It defines a slider, seen on top, that can be dragged. Once dragged, it changes the value of the variable "order" and the whole block of code gets evaluated. This principle can be seen in various examples presented on the pages above! {{{#!sagecell x = SR.var('x') x0 = 0 f = sin(x) * e^(-x) p = plot(f, -1, 5, thickness=2) dot = point((x0, f(x=x0)), pointsize=80, rgbcolor=(1, 0, 0)) |
| Line 16: | Line 49: |
| def _(N=selector([1..8*13], ncols=8, width=10, default=10)): A = J0(N) print A.cuspidal_subgroup() |
def _(order=slider([1 .. 12])): ft = f.taylor(x, x0, order) pt = plot(ft, -1, 5, color='green', thickness=2) pretty_print(html(r'$f(x)\;=\;%s$' % latex(f))) pretty_print(html(r'$\hat{f}(x;%s)\;=\;%s+\mathcal{O}(x^{%s})$' % (x0, latex(ft), order+1))) show(dot + p + pt, ymin=-.5, ymax=1) |
| Line 20: | Line 56: |
attachment:cuspgroup.png |
{{attachment:taylor_series_animated.gif}} |
Sage Interactions
This is a collection of pages demonstrating the use of the **interact** command in Sage. It should be easy to just scroll through and copy/paste examples into Sage notebooks. If you have suggestions on how to improve interact, add them here or email the sage-support mailing list. Of course, your own examples are also welcome!
Documentation links:
interacts in the Jupyter notebook (see this page and the two following ones)
interacts in the legacy SageNB notebook (many helpful examples)
Examples:
Explanatory example: Taylor Series
This is the code and a mockup animation of the interact command. It defines a slider, seen on top, that can be dragged. Once dragged, it changes the value of the variable "order" and the whole block of code gets evaluated. This principle can be seen in various examples presented on the pages above!