Sage Interactions - Differential Equations

goto interact main page

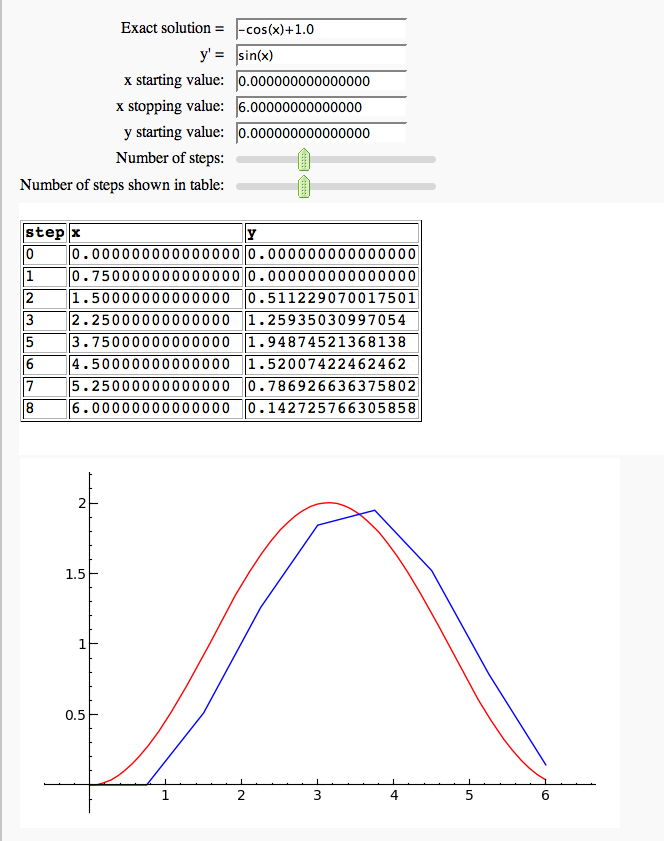
Euler's Method in one variable

by Marshall Hampton. This needs some polishing but its usable as is.

xxxxxxxxxx

def tab_list(y, headers = None):

    '''

    Converts a list into an html table with borders.

    '''

    s = '<table border = 1>'

    if headers:

        for q in headers:

            s = s + '<th>' + str(q) + '</th>'

    for x in y:

        s = s + '<tr>'

        for q in x:

            s = s + '<td>' + str(q) + '</td>'

        s = s + '</tr>'

    s = s + '</table>'

    return s

var('x y')

@interact

def euler_method(y_exact_in = input_box('-cos(x)+1.0', type = str, label = 'Exact solution = '), y_prime_in = input_box('sin(x)', type = str, label = "y' = "), start = input_box(0.0, label = 'x starting value: '), stop = input_box(6.0, label = 'x stopping value: '), startval = input_box(0.0, label = 'y starting value: '), nsteps = slider([2^m for m in range(0,10)], default = 10, label = 'Number of steps: '), show_steps = slider([2^m for m in range(0,10)], default = 8, label = 'Number of steps shown in table: ')):

    y_exact = lambda x: eval(y_exact_in)

    y_prime = lambda x,y: eval(y_prime_in)

    stepsize = float((stop-start)/nsteps)

    steps_shown = min(nsteps,show_steps)

    sol = [startval]

    xvals = [start]

    for step in range(nsteps):

        sol.append(sol[-1] + stepsize*y_prime(xvals[-1],sol[-1]))

        xvals.append(xvals[-1] + stepsize)

    sol_max = max(sol + [find_local_maximum(y_exact,start,stop)[0]])

    sol_min = min(sol + [find_local_minimum(y_exact,start,stop)[0]])

    show(plot(y_exact(x),start,stop,rgbcolor=(1,0,0))+line([[xvals[index],sol[index]] for index in range(len(sol))]),xmin=start,xmax = stop, ymax = sol_max, ymin = sol_min)

    if nsteps < steps_shown:

        table_range = list(range(len(sol)))

    else:

        table_range = list(range(floor(steps_shown/2))) + list(range(len(sol)-floor(steps_shown/2),len(sol)))

    pretty_print(html(tab_list([[i,xvals[i],sol[i]] for i in table_range], headers = ['step','x','y'])))

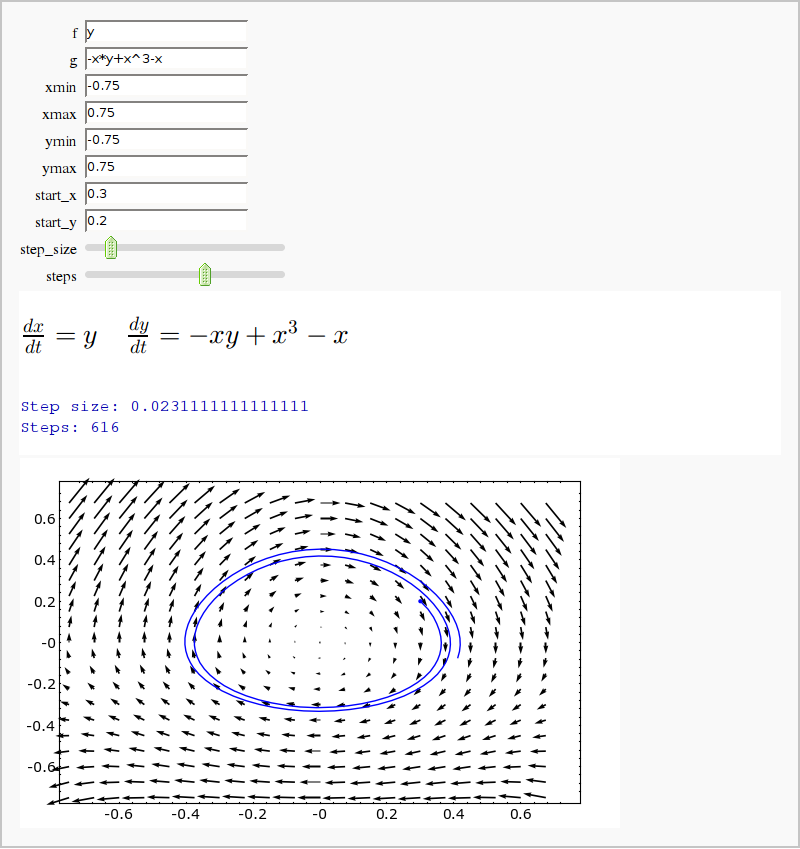
Vector Fields and Euler's Method

by Mike Hansen (tested and updated by William Stein, and later by Dan Drake)

xxxxxxxxxx

x,y = var('x,y')

from sage.ext.fast_eval import fast_float

@interact

def _(f = input_box(default=y), g=input_box(default=-x*y+x^3-x),

      xmin=input_box(default=-1), xmax=input_box(default=1),

      ymin=input_box(default=-1), ymax=input_box(default=1),

      start_x=input_box(default=0.5), start_y=input_box(default=0.5),

      step_size=(0.01,(0.001, 0.2)), steps=(600,(0, 1400)) ):

    ff = fast_float(f, 'x', 'y')

    gg = fast_float(g, 'x', 'y')

    steps = int(steps)

​

    points = [ (start_x, start_y) ]

    for i in range(steps):

        xx, yy = points[-1]

        try:

            points.append( (xx + step_size * ff(xx,yy), yy + step_size * gg(xx,yy)) )

        except (ValueError, ArithmeticError, TypeError):

            break

​

    starting_point = point(points[0], pointsize=50)

    solution = line(points)

    vector_field = plot_vector_field( (f,g), (x,xmin,xmax), (y,ymin,ymax) )

​

    result = vector_field + starting_point + solution

​

    pretty_print(html(r"$\displaystyle\frac{dx}{dt} = %s$  $ \displaystyle\frac{dy}{dt} = %s$" % (latex(f),latex(g))))

    result.show(xmin=xmin,xmax=xmax,ymin=ymin,ymax=ymax)

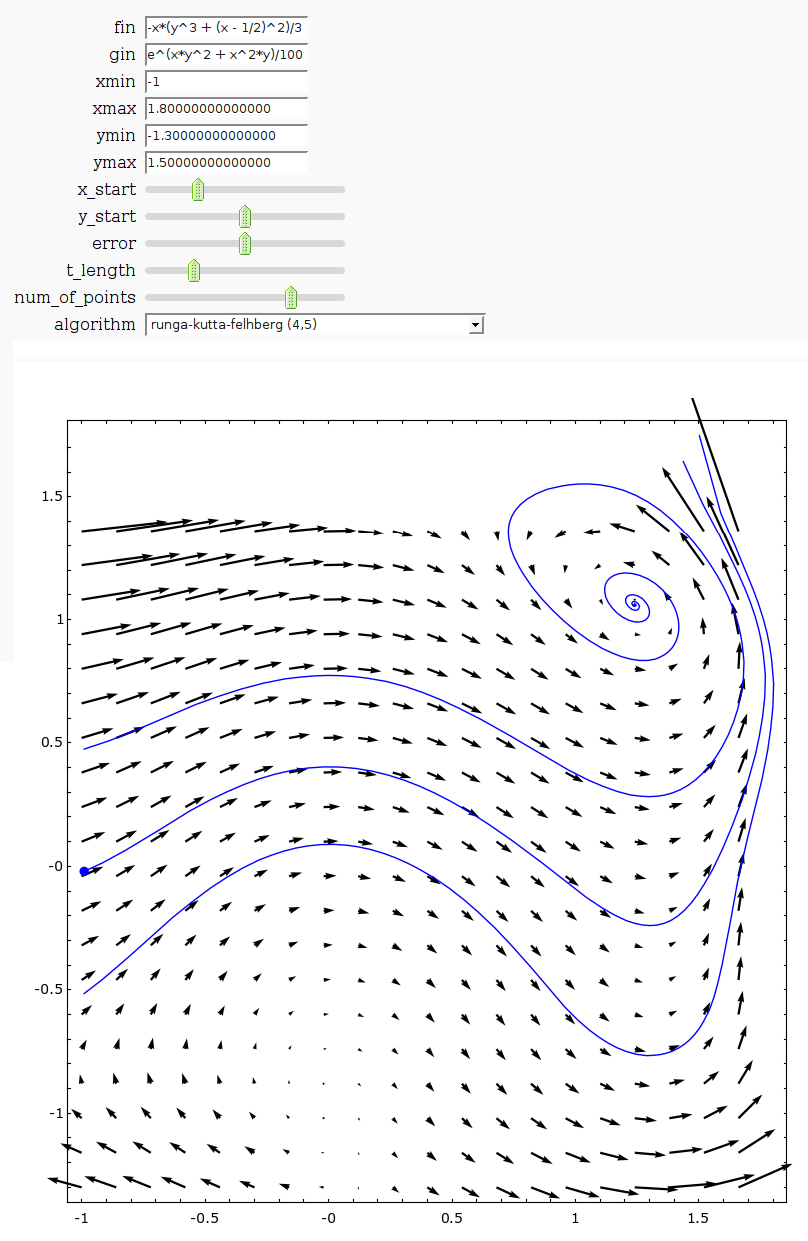
Vector Field with Runga-Kutta-Fehlberg

by Harald Schilly

xxxxxxxxxx

# Solve ODEs using sophisticated Methods like Runga-Kutta-Fehlberg

# by Harald Schilly, April 2008

# (jacobian doesn't work, please fix ...)

var('x y')

@interact

def _(fin = input_box(default=y+exp(x/10)-1/3*((x-1/2)^2+y^3)*x-x*y^3), gin=input_box(default=x^3-x+1/100*exp(y*x^2+x*y^2)-0.7*x),

      xmin=input_box(default=-1), xmax=input_box(default=1.8),

      ymin=input_box(default=-1.3), ymax=input_box(default=1.5),

      x_start=(-1,(-2,2)), y_start=(0,(-2,2)), error=(0.5,(0,1)),

      t_length=(23,(0, 100)) , num_of_points = (1500,(5,2000)),

      algorithm = selector([

         ("rkf45" , "runga-kutta-felhberg (4,5)"),

         ("rk2" , "embedded runga-kutta (2,3)"),

         ("rk4" , "4th order classical runga-kutta"),

         ("rk8pd" , 'runga-kutta prince-dormand (8,9)'),

         ("rk2imp" , "implicit 2nd order runga-kutta at gaussian points"),

         ("rk4imp" , "implicit 4th order runga-kutta at gaussian points"),

         ("bsimp" , "implicit burlisch-stoer (requires jacobian)"),

         ("gear1" , "M=1 implicit gear"),

         ("gear2" , "M=2 implicit gear")

      ])):

    f(x,y)=fin

    g(x,y)=gin

​

    ff = f._fast_float_(*f.args())

    gg = g._fast_float_(*g.args())

​

    #solve

    path = []

    err = error

    xerr = 0

    for yerr in [-err, 0, +err]:

      T=ode_solver()

      T.algorithm=algorithm

      T.function = lambda t, yp: [ff(yp[0],yp[1]), gg(yp[0],yp[1])]

      T.jacobian = lambda t, yp: [[diff(fun,dval)(yp[0],yp[1]) for dval in [x,y]] for fun in [f,g]]

      T.ode_solve(y_0=[x_start + xerr, y_start + yerr],t_span=[0,t_length],num_points=num_of_points)

      path.append(line([p[1] for p in T.solution]))

​

    #plot

    vector_field = plot_vector_field( (f,g), (x,xmin,xmax), (y,ymin,ymax) )

    starting_point = point([x_start, y_start], pointsize=50)

    show(vector_field + starting_point + sum(path), aspect_ratio=1, figsize=[8,9])

Linear two-dimensional ODEs

by Marshall Hampton

%cython
cpdef c_euler_m(double t0, double x10, double x20, double tend, int steps, double a11, double a12, double a21, double a22, double cutoff = 10):
    cdef double h = (tend-t0)/steps
    traj = [[x10,x20]]
    cdef double x1current = x10
    cdef double x2current = x20
    cdef int i
    cdef double newx1
    cdef double newx2
    for i in range(0,steps):
        newx1 = x1current + h*a11*x1current + h*a12*x2current
        newx2 = x2current + h*a21*x1current + h*a22*x2current
        if newx1 > cutoff or newx2 > cutoff or newx1 < -cutoff or newx2 < -cutoff:
            break
        traj.append([newx1,newx2])
        x1current = newx1
        x2current = newx2
    return traj

@interact
def planarsystem(a11 = slider(srange(-10,10,1/10),default = -1), a12 = slider(srange(-10,10,1/10),default = -1), a21 = slider(srange(-10,10,1/10),default = 1), a22 = slider(srange(-10,10,1/10),default = -1), time_tracked = slider(srange(1,100,1.0),default=10)):
    A = matrix(RDF,[[a11,a12],[a21,a22]])
    eigs = A.eigenvalues()
    pretty_print(html('<center>$x\' = Ax$ dynamics<BR>$A = '+latex(A)+'$, eigenvalues: $%2.2f + %2.2fI, %2.2f + %2.2fI$</center>'%(eigs[0].real(),eigs[0].imag(),eigs[1].real(),eigs[1].imag())))
    trajs = Graphics()
    for q in srange(0,2*pi,.15):
        astart = randint(1,10)
        ntraj = c_euler_m(0,cos(q),sin(q),time_tracked,300,a11,a12,a21,a22)
        for i in range(astart,len(ntraj)-1,10):
            trajs = trajs + arrow(ntraj[i],ntraj[i+1],width=1, arrowsize=2)
        trajs = trajs + line(ntraj)
        ntraj = c_euler_m(0,cos(q),sin(q),-time_tracked,300,a11,a12,a21,a22)
        trajs = trajs + line(ntraj)
        for i in range(astart,len(ntraj)-1,10):
            trajs = trajs + arrow(ntraj[i+1],ntraj[i],width=1, arrowsize=2)
    show(trajs, figsize = [6,6], xmin = -1, xmax = 1, ymin = -1, ymax = 1)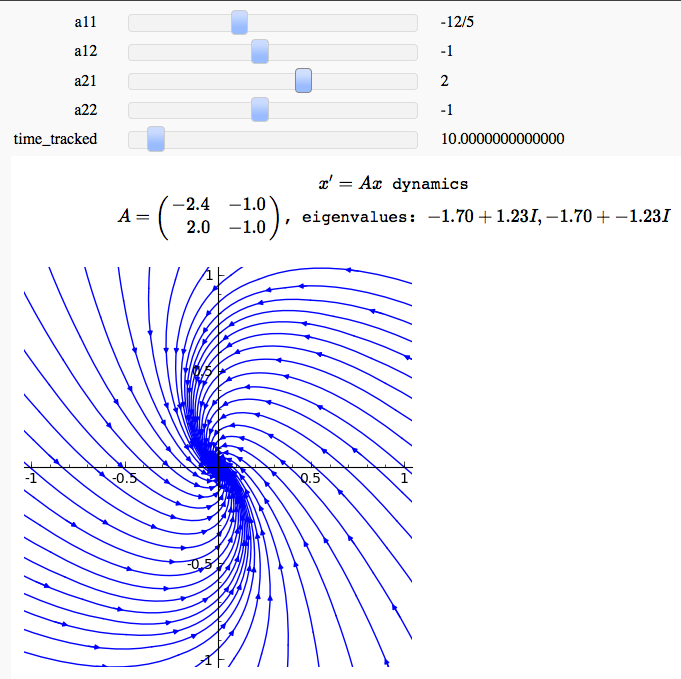

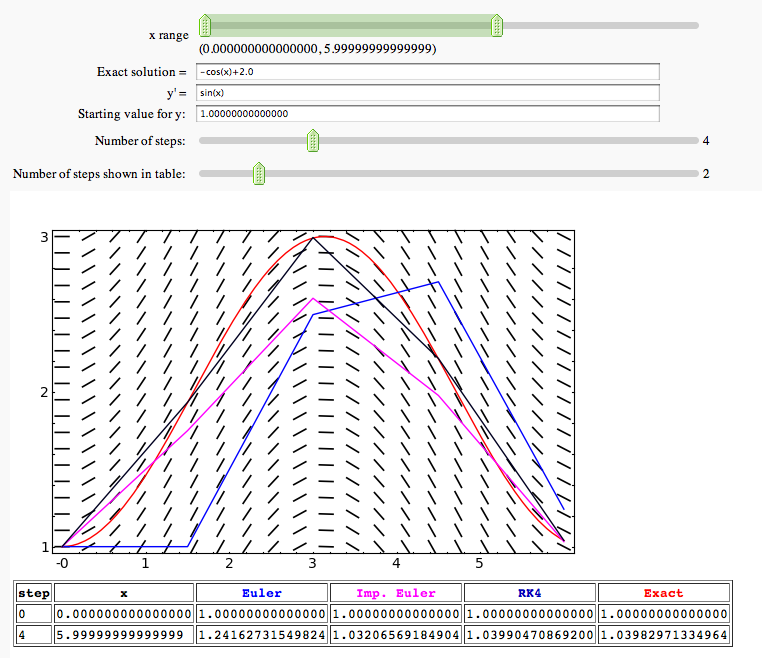
Euler's Method, Improved Euler, and 4th order Runge-Kutta in one variable

by Marshall Hampton. This is a more baroque version of the Euler's method demo above.

xxxxxxxxxx

def ImpEulerMethod(xstart, ystart, xfinish, nsteps, f):

    sol = [ystart]

    xvals = [xstart]

    h = N((xfinish-xstart)/nsteps)

    for step in range(nsteps):

        k1 = f(xvals[-1],sol[-1])

        k2 = f(xvals[-1] + h,sol[-1] + k1*h)

        sol.append(sol[-1] + h*(k1+k2)/2)

        xvals.append(xvals[-1] + h)

    return list(zip(xvals,sol))

def RK4Method(xstart, ystart, xfinish, nsteps, f):

    sol = [ystart]

    xvals = [xstart]

    h = N((xfinish-xstart)/nsteps)

    for step in range(nsteps):

        k1 = f(xvals[-1],sol[-1])

        k2 = f(xvals[-1] + h/2,sol[-1] + k1*h/2)

        k3 = f(xvals[-1] + h/2,sol[-1] + k2*h/2)

        k4 = f(xvals[-1] + h,sol[-1] + k3*h)

        sol.append(sol[-1] + h*(k1+2*k2+2*k3+k4)/6)

        xvals.append(xvals[-1] + h)

    return list(zip(xvals,sol))

def tab_list(y, headers = None):

    '''

    Converts a list into an html table with borders.

    '''

    s = '<table border = 1>'

    if headers:

        for q in headers:

            s = s + '<th>' + str(q) + '</th>'

    for x in y:

        s = s + '<tr>'

        for q in x:

            s = s + '<td>' + str(q) + '</td>'

        s = s + '</tr>'

    s = s + '</table>'

    return s

var('x, y')

@interact

def euler_method(q = range_slider(0,10,.1,(0,6),'x range'), y_exact_in = input_box('-cos(x)+2.0', type = str, label = 'Exact solution = '), y_prime_in = input_box('sin(x)', type = str, label = "y' = "), startval = input_box(1.0, label = 'Starting value for y: '), nsteps = slider([2^m for m in range(0,10)], default = 10, label = 'Number of steps: '), show_steps = slider([2^m for m in range(0,10)], default = 8, label = 'Number of steps shown in table: ')):

    start = q[0]

    stop = q[1]

    y_exact = lambda x: eval(y_exact_in)

    y_prime = lambda x,y: eval(y_prime_in)

    stepsize = float((stop-start)/nsteps)

    steps_shown = min(nsteps,show_steps)

    sol2 = ImpEulerMethod(start, startval, stop, nsteps, y_prime)

    sol3 = RK4Method(start, startval, stop, nsteps, y_prime)

    sol = [startval]

    xvals = [start]

    for step in range(nsteps):

        sol.append(sol[-1] + stepsize*y_prime(xvals[-1],sol[-1]))

        xvals.append(xvals[-1] + stepsize)

    sol_max = max(sol + [find_local_maximum(y_exact,start,stop)[0]])

    sol_min = min(sol + [find_local_minimum(y_exact,start,stop)[0]])

    slopes = plot_slope_field(y_prime(x=x,y=y), (start,stop), (sol_min, sol_max))

    exact_plot = plot(y_exact(x),start,stop,rgbcolor=(1,0,0))

    euler_plot = line([[xvals[index],sol[index]] for index in range(len(sol))])

    rk4_plot = line(sol3, rgbcolor = (0,0,.125))

    imp_plot = line(sol2, rgbcolor = (1,0,1))

    show(slopes +exact_plot + euler_plot + imp_plot+ rk4_plot,xmin=start,xmax = stop, ymax = sol_max, ymin = sol_min)

    if nsteps < steps_shown:

        table_range = list(range(len(sol)))

    else:

        table_range = list(range(floor(steps_shown/2))) + list(range(len(sol)-floor(steps_shown/2),len(sol)))

    html(tab_list([[i,xvals[i],sol[i],sol2[i][1],sol3[i][1],y_exact(xvals[i])] for i in table_range], headers = ['step','x','<font color="#0000FF">Euler</font>','<font color="#FF00FF">Imp. Euler</font>', '<font color="#0000bb">RK4</font>','<font color="#FF0000">Exact</font>']))

Mass/Spring systems

by Jason Grout

These two interacts involve some Cython code or other scipy imports, so I've posted a file containing them. You can download the worksheet or copy it online.

• https://sage.math.washington.edu/home/pub/42

• https://sage.math.washington.edu/home/pub/43

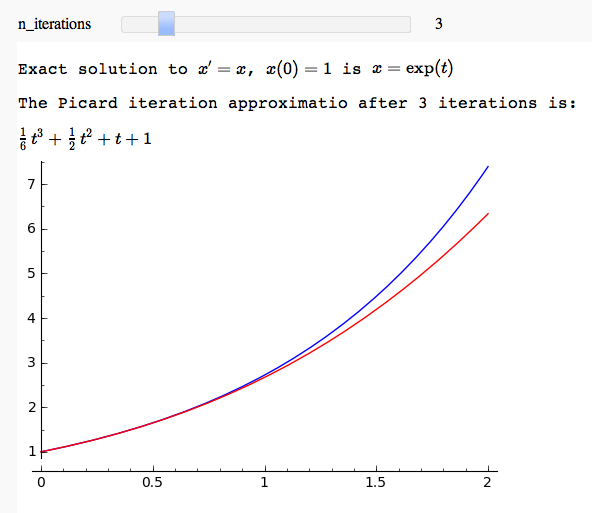
Picard iteration example

by Marshall Hampton and David Joyner

xxxxxxxxxx

def picard_iteration(f, a, c, iterations):

    r'''

    Computes the N-th Picard iterate for the IVP  

​

        x' = f(t,x), x(a) = c.

​

    EXAMPLES::

​

        sage: var('x t s')

        (x, t, s)

        sage: a = 0; c = 2

        sage: f = lambda t,x: 1-x

        sage: picard_iteration(f, a, c, 0)

        2

         sage: picard_iteration(f, a, c, 1)

        2 - t

        sage: picard_iteration(f, a, c, 2)

        t^2/2 - t + 2

        sage: picard_iteration(f, a, c, 3)

        -t^3/6 + t^2/2 - t + 2

    '''

    if iterations == 0:

        return c

    if iterations == 1:

        x0 = lambda t: c + integral(f(t=s,x=c), s, a, t)

        return expand(x0(t))

    for i in range(iterations):

        x_old = lambda s: picard_iteration(f, a, c, iterations-1).subs(t=s)

        x0 = lambda t: c + integral(f(t=s,x=x_old(s)), s, a, t)

    return expand(x0(t))

​

@interact

def picarder(n_iterations = slider(0,20,1,default = 2)):

    var('x,t,s')

    f = lambda t,x:x

    html(r"Exact solution to $x' = x$, $x(0) = 1$ is $x = \exp(t)$<br>")

    pic = picard_iteration(f,0,1,n_iterations)

    html('The Picard iteration approximation after ' + str(n_iterations) + ' iterations is:<br>')

    html('$'+latex(pic)+'$')

    exact = plot(exp(t),(t,0,2))

    pic_plot = plot(pic,(t,0,2), rgbcolor = (1,0,0))

    show(exact + pic_plot)

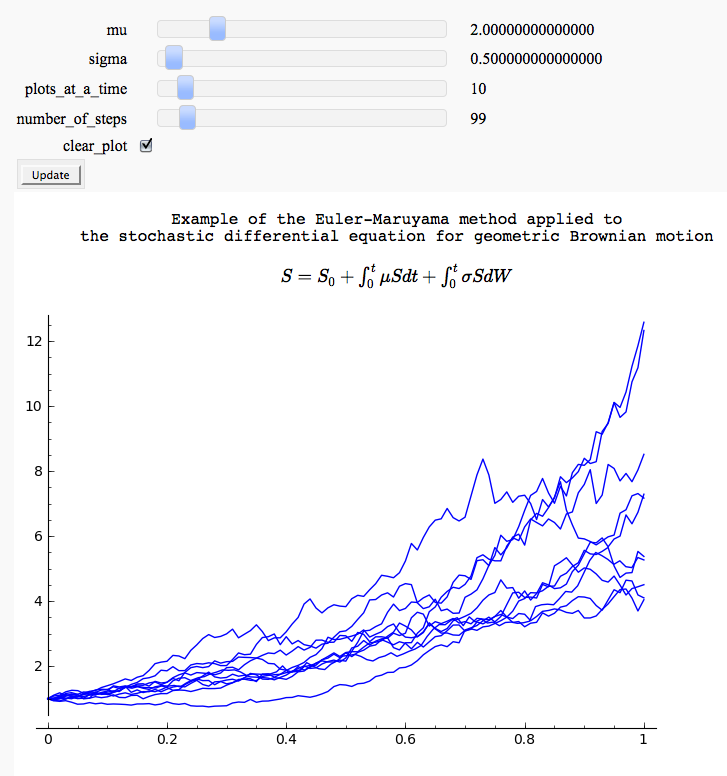
Euler-Maruyama method and geometric Brownian motion (a common simple model of the stock market)

by Marshall Hampton

xxxxxxxxxx

def EulerMaruyama(xstart, ystart, xfinish, nsteps, f1, f2): 

    sol = [ystart] 

    xvals = [xstart] 

    h = N((xfinish-xstart)/nsteps) 

    for step in range(nsteps): 

        sol.append(sol[-1] + h*f1(sol[-1]) + h^(.5)*f2(sol[-1])*normalvariate(0,1)) 

        xvals.append(xvals[-1] + h) 

    return list(zip(xvals,sol))

out = Graphics()

save(out,'temp')

@interact

def EulerMaruyamaExample(mu = slider(srange(0,10,.1),default=2.0),

                        sigma = slider(srange(0,10,.1),default=0.5),

                        plots_at_a_time = slider(range(1,100),default=10), 

                        number_of_steps = slider(range(1,1000),default=100), 

                        clear_plot = checkbox(True), 

                        auto_update=False):

    html('<center>Example of the Euler-Maruyama method applied to<br>the stochastic differential equation for geometric Brownian motion</center>')

    html(r'<center>$S = S_0 + \int_0^t \mu S dt + \int_0^t \sigma S dW$</center>')

    emplot = list_plot(EulerMaruyama(0,1,1,number_of_steps,lambda x: mu*x,lambda x:sigma*x),plotjoined=True)

    for i in range(1,plots_at_a_time):

        emplot = emplot + list_plot(EulerMaruyama(0,1,1,100,lambda x: mu*x,lambda x:sigma*x),plotjoined=True)

    if clear_plot:

        out = emplot

        save(out,'temp')

    else:

        out = load('temp')

        out = out + emplot

        save(out,'temp')

    show(out, figsize = [8,5])

Autonomous equations and stable/unstable fixed points

by Marshall Hampton This needs the Cython functon defined in a seperate cell. Note that it is not a particularly good example of Cython use.

%cython
cpdef RK4_1d(f, double t_start, double y_start, double t_end, int steps, double y_upper = 10**6, double y_lower = -10**6):
    '''
    Fourth-order scalar Runge-Kutta solver with fixed time steps. f must be a function of t,y, 
    where y is just a scalar variable.
    '''
    cdef double step_size = (t_end - t_start)/steps
    cdef double t_current = t_start
    cdef double y_current = y_start
    cdef list answer_table = []
    cdef int j
    answer_table.append([t_current,y_current])
    for j in range(0,steps):
        k1=f(t_current, y_current)
        k2=f(t_current+step_size/2, y_current + k1*step_size/2)
        k3=f(t_current+step_size/2, y_current + k2*step_size/2)
        k4=f(t_current+step_size, y_current + k3*step_size)
        t_current += step_size
        y_current = y_current + (step_size/6)*(k1+2*k2+2*k3+k4)
        if y_current > y_upper or y_current < y_lower: 
            j = steps
        answer_table.append([t_current,y_current])
    return answer_table

from sage.rings.polynomial.real_roots import *
var('x')
@interact
def autonomous_plot(poly=input_box(x*(x-1)*(x-2),label='polynomial'), t_end = slider(1,10,step_size = .1)): 
    var('x')   
    y = polygen(ZZ)
    ypoly = sage_eval(repr(poly).replace('x','y'),locals=locals())
    rr = real_roots(ypoly, max_diameter = 1/100)
    eps = 0.2
    delvals = .04
    minr = min([x[0][0] for x in rr])
    maxr = max([x[0][1] for x in rr])
    svals = [(minr-eps)*t+(1-t)*(maxr+eps) for t in srange(0,1+delvals,delvals)]
    def polyf(t,xi):
        return poly(x=xi)
    paths = [RK4_1d(polyf,0.0,q,t_end,100.0) for q in svals]    
    miny = max(minr-eps,min([min([q1[1] for q1 in q]) for q in paths]))
    maxy = min(maxr+eps,max([max([q1[1] for q1 in q]) for q in paths]))
    solpaths = sum([line(q) for q in paths])
    fixedpoints = sum([line([[0,(q[0][0]+q[0][1])/2],[t_end,(q[0][0]+q[0][1])/2]], rgbcolor = (1,0,0)) for q in rr])
    var('t')
    html("Autonomous differential equation $x' = p(x)$")
    show(solpaths+fixedpoints, ymin = miny, ymax = maxy, xmin = 0, xmax = t_end, figsize = [6,4])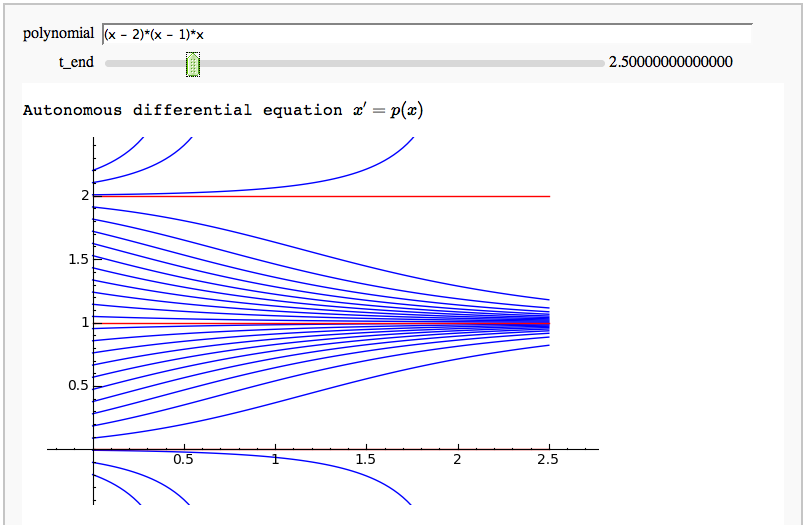

Heat equation using Fourier series

by Pablo Angulo

xxxxxxxxxx

var('x')

x0  = 0

k=1

f   = x*exp(-x^2)

p   = plot(f,0,2*pi, thickness=2)

c   = 1/pi

orden=10

alpha=[(n,c*numerical_integral(f*sin(x*n/2),0,2*pi)[0] ) for n in range(1,orden)]

​

@interact

def _(tiempo = (0.1*j for j in (0..10)) ):

    ft = sum( a*sin(x*n/2)*exp(-k*(n/2)^2*tiempo) for n,a in alpha)

    pt = plot(ft, 0, 2*pi, color='green', thickness=2)

    show( p + pt, ymin = -.2)

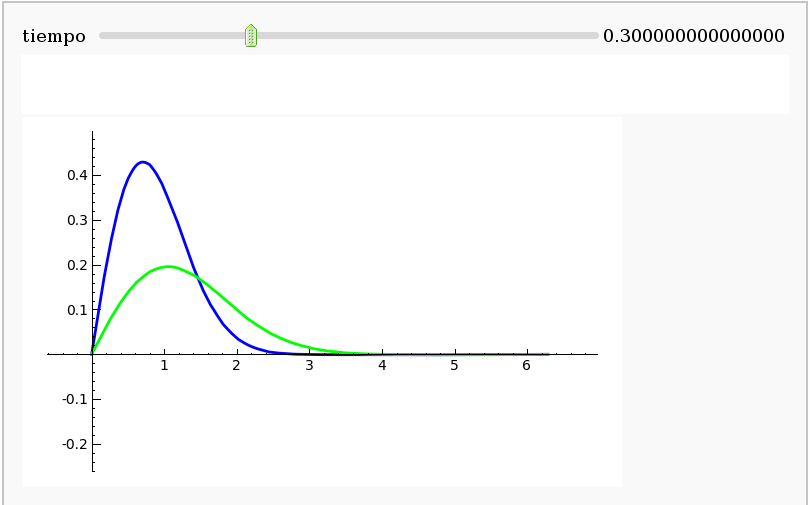
Heat equation using finite diferences in cython

by Pablo Angulo

%cython
#cython code implementing a very simple finite diference scheme
import numpy as np
def calor_cython(u0,float dx, float k,float t_f,int tsteps):
    cdef int m
    cdef float dt
    cdef float s
    u=np.array(u0)
    dt=t_f/tsteps
    s=k*dt/(dx**2)        #we cannot use ^ for exponentiation in cython
    for m in range(tsteps):
        u[1:-1]=(1-2*s)*u[1:-1]+s*u[0:-2]+s*u[2:]
    return u

#interact box wrapping the code above
var('x')

@interact
def _(f=input_box(default=x*exp(-x^2),label='f(x)'), longitud=input_box(default=2*pi),
      tiempo=input_box(default=0.1), M=input_box(default=100),
      k=input_box(default=1), tsteps=input_box(default=2000) ):
    efe=f._fast_float_(x)
    dx=float(longitud/M)
    xs=[n*dx for n in range(M+1)]
    u0=[efe(a) for a in xs]

    s=k*(tiempo/tsteps) /dx^2
    if s>0.5:
        print('s=%f > 1/2!!!  The method is not stable' % s)

    ut=calor_cython(u0,dx,k,tiempo,tsteps)
    show( line2d(list(zip(xs, u0))) + line2d(list(zip(xs, ut)), rgbcolor='green') )

DE with boundary values

The following interact demo looks at the DE+BC y'+y=0, y(0)=a, y(b)=c, and has a slider for b. When b=pi "problems arise":-)

xxxxxxxxxx

var('x')

@interact

def BCs(b=input_box(1,label='BC at far endpoint'), c = slider(1,5,step_size = .01), a = 1): 

    P1 = text(r"$y''+y=0,\ y(0) = a,\ y(b) = c$",(4,-1/(c-3.14152)))

    P2 = plot(a*cos(x)+(b-a*cos(c))*sin(x)/sin(c),x,0,5)

    (P1+P2).show()

de-interact-with-BCs.sws