Sage Interactions - Linear Algebra
goto interact main page
Contents
-
Sage Interactions - Linear Algebra
- Numerical instability of the classical Gram-Schmidt algorithm
- Equality of det(A) and det(A.tranpose())
- Linear transformations
- Gerschgorin Circle Theorem
- Singular value decomposition
- Discrete Fourier Transform
- The Gauss-Jordan method for inverting a matrix
- Solution of an homogeneous system of linear equations
- Solution of a non homogeneous system of linear equations
Numerical instability of the classical Gram-Schmidt algorithm
by Marshall Hampton
xxxxxxxxxxdef GS_classic(a_list): ''' Given a list of vectors or a matrix, returns the QR factorization using the classical (and numerically unstable) Gram-Schmidt algorithm. ''' if type(a_list) != list: cols = a_list.cols() a_list = [x for x in cols] indices = range(len(a_list)) q = [] r = [[0 for i in indices] for j in indices] v = [a_list[i][:] for i in indices] for i in indices: for j in range(0,i): r[j][i] = q[j].inner_product(a_list[i]) v[i] = v[i] - r[j][i]*q[j] r[i][i] = (v[i]*v[i])**(1/2) q.append(v[i]/r[i][i]) q = matrix([q[i] for i in indices]).transpose() return q, matrix(r)def GS_modern(a_list): ''' Given a list of vectors or a matrix, returns the QR factorization using the 'modern' Gram-Schmidt algorithm. ''' if type(a_list) != list: cols = a_list.cols() a_list = [x for x in cols] indices = range(len(a_list)) q = [] r = [[0 for i in indices] for j in indices] v = [a_list[i][:] for i in indices] for i in indices: r[i][i] = v[i].norm(2) q.append(v[i]/r[i][i]) for j in range(i+1, len(indices)): r[i][j] = q[i].inner_product(v[j]) v[j] = v[j] - r[i][j]*q[i] q = matrix([q[i] for i in indices]).transpose() return q, matrix(r)pretty_print(html('<h2>Numerical instability of the classical Gram-Schmidt algorithm</h2>'))def gstest(precision = slider(range(3,53), default = 10), a1 = input_box([1,1/1000,1/1000]), a2 = input_box([1,1/1000,0]), a3 = input_box([1,0,1/1000])): myR = RealField(precision) displayR = RealField(5) pretty_print(html('precision in bits: ' + str(precision) + '<br>')) A = matrix([a1,a2,a3]) A = [vector(myR,x) for x in A] qn, rn = GS_classic(A) qb, rb = GS_modern(A) pretty_print(html('Classical Gram-Schmidt:')) show(matrix(displayR,qn)) pretty_print(html('Stable Gram-Schmidt:')) show(matrix(displayR,qb))
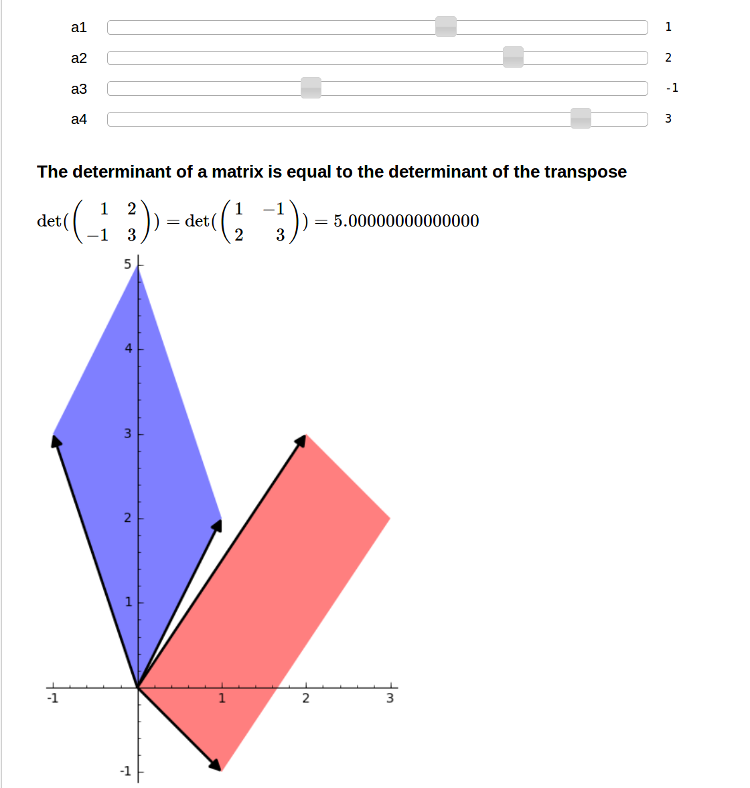
Equality of det(A) and det(A.tranpose())
by Marshall Hampton
xxxxxxxxxxsrg = srange(-4,4,1/10,include_endpoint=True)def dualv(a1=slider(srg,default=1),a2=slider(srg,default=2), a3=slider(srg,default=-1),a4=slider(srg,default=3)): A1 = arrow2d([0,0],[a1,a2],rgbcolor='black') A2 = arrow2d([0,0],[a3,a4],rgbcolor='black') A3 = arrow2d([0,0],[a1,a3],rgbcolor='black') A4 = arrow2d([0,0],[a2,a4],rgbcolor='black') p1 = polygon([[0,0],[a1,a2],[a1+a3,a2+a4],[a3,a4],[0,0]], alpha=.5) p2 = polygon([[0,0],[a1,a3],[a1+a2,a3+a4],[a2,a4],[0,0]],rgbcolor='red', alpha=.5) A = matrix([[a1,a2],[a3,a4]]) pretty_print(html('<h3>The determinant of a matrix is equal to the determinant of the transpose</h3>')) pretty_print(html("$\det(%s) = \det(%s)=%s$"%(latex(A),latex(A.transpose()),latex(RR(A.determinant()))))) show(A1+A2+A3+A4+p1+p2)
Linear transformations
by Jason Grout
A square matrix defines a linear transformation which rotates and/or scales vectors. In the interact command below, the red vector represents the original vector (v) and the blue vector represents the image w under the linear transformation. You can change the angle and length of v by changing theta and r.
xxxxxxxxxxdef linear_transformation(A=matrix([[1,-1],[-1,1/2]]),theta=slider(0, 2*pi, .1), r=slider(0.1, 2, .1, default=1)): v=vector([r*cos(theta), r*sin(theta)]) w = A*v circles = sum([circle((0,0), radius=i, color='black') for i in [1..2]]) pretty_print(html("$%s %s=%s$"%tuple(map(latex, [A, v.column().n(4), w.column().n(4)])))) show(v.plot(color='red')+w.plot(color='blue')+circles,aspect_ratio=1)
Gerschgorin Circle Theorem
by Marshall Hampton. This animated version requires convert (imagemagick) to be installed, but it can easily be modified to a static version. The animation illustrates the idea behind the stronger version of Gerschgorin's theorem, which says that if the disks around the eigenvalues are disjoint then there is one eigenvalue per disk. The proof is by continuity of the eigenvalues under a homotopy to a diagonal matrix.
xxxxxxxxxxfrom scipy import linalgpretty_print(html('<h2>The Gerschgorin circle theorem</h2>'))def Gerschgorin(Ain = input_box(default='[[10,1,1/10,0],[-1,9,0,1],[1,0,2,3/10],[-.5,0,-.3,1]]', type = str, label = 'A = '), an_size = slider(1,100,1,1.0)): A = sage_eval(Ain) size = len(A) pretty_print(html('$A = ' + latex(matrix(RealField(10),A))+'$')) A = matrix(RealField(10),A) B = [[0 for i in range(size)] for j in range(size)] for i in range(size): B[i][i] = A[i][i] B = matrix(B) frames = [] centers = [(real(q),imag(q)) for q in [A[i][i] for i in range(size)]] radii_row = [sum([abs(A[i][j]) for j in range(i)+range(i+1,size)]) for i in range(size)] radii_col = [sum([abs(A[j][i]) for j in range(i)+range(i+1,size)]) for i in range(size)] x_min = min([centers[i][0]-radii_row[i] for i in range(size)]+[centers[i][0]-radii_col[i] for i in range(size)]) x_max = max([centers[i][0]+radii_row[i] for i in range(size)]+[centers[i][0]+radii_col[i] for i in range(size)]) y_min = min([centers[i][1]-radii_row[i] for i in range(size)]+[centers[i][1]-radii_col[i] for i in range(size)]) y_max = max([centers[i][1]+radii_row[i] for i in range(size)]+[centers[i][1]+radii_col[i] for i in range(size)]) if an_size > 1: t_range= srange(0,1+1/an_size,1/an_size) else: t_range = [1] for t in t_range: C = t*A + (1-t)*B eigs = [CDF(x) for x in linalg.eigvals(C.numpy())] eigpoints = points([(real(q),imag(q)) for q in eigs],pointsize = 10, rgbcolor = (0,0,0)) centers = [(real(q),imag(q)) for q in [A[i][i] for i in range(size)]] radii_row = [sum([abs(C[i][j]) for j in range(i)+range(i+1,size)]) for i in range(size)] radii_col = [sum([abs(C[j][i]) for j in range(i)+range(i+1,size)]) for i in range(size)] scale = max([(x_max-x_min),(y_max-y_min)]) scale = 7/scale row_circles = sum([circle(centers[i],radii_row[i],fill=True, alpha = .3) for i in range(size)]) col_circles = sum([circle(centers[i],radii_col[i],fill=True, rgbcolor = (1,0,0), alpha = .3) for i in range(size)]) ft = eigpoints+row_circles+col_circles frames.append(ft) show(animate(frames,figsize = [(x_max-x_min)*scale,(y_max-y_min)*scale], xmin = x_min, xmax=x_max, ymin = y_min, ymax = y_max))
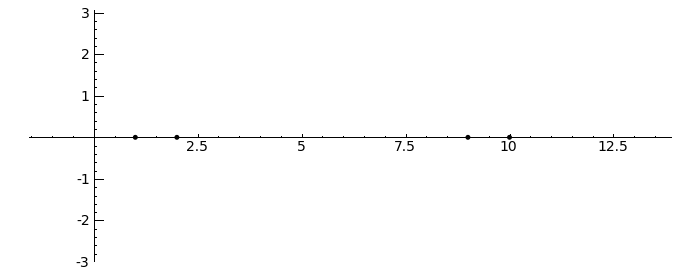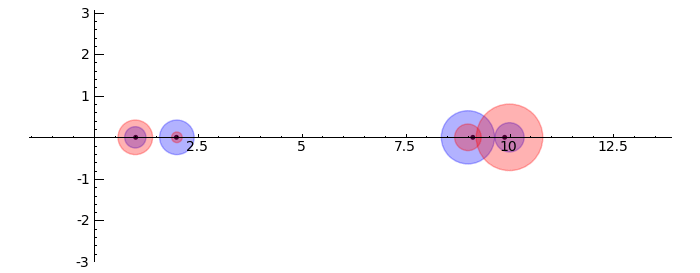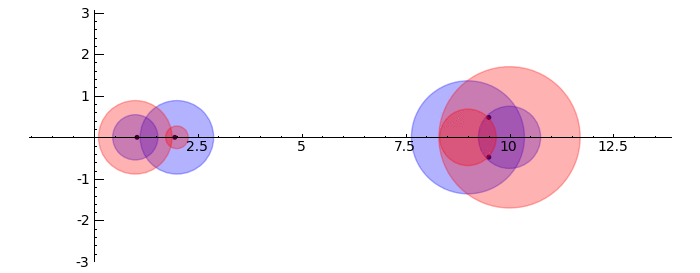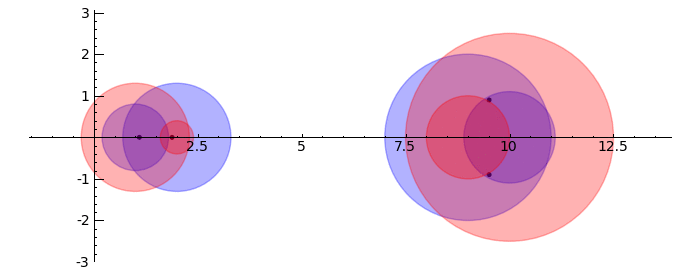
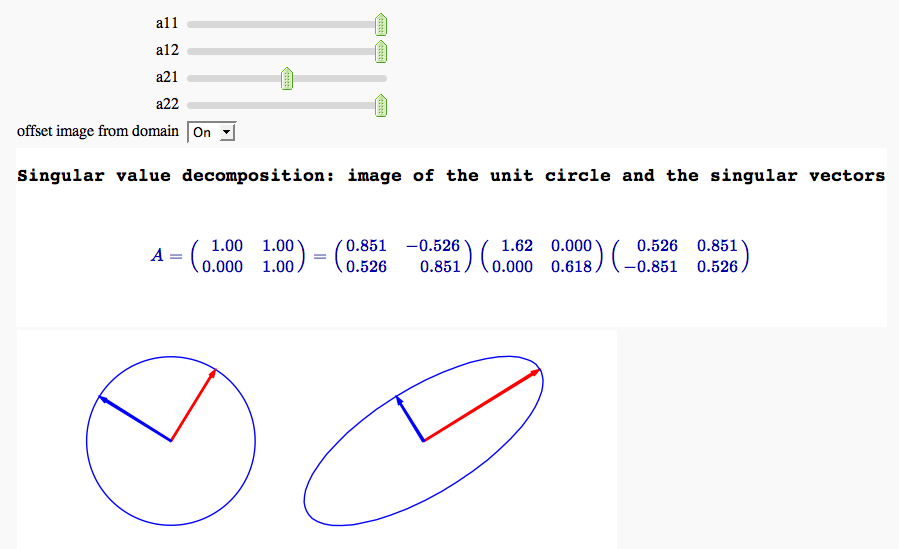
Singular value decomposition
by Marshall Hampton
xxxxxxxxxximport scipy.linalg as linvar('t')def rotell(sig,umat,t,offset=0): temp = matrix(umat)*matrix(2,1,[sig[0]*cos(t),sig[1]*sin(t)]) return [offset+temp[0][0],temp[1][0]]def svd_vis(a11=slider(-1,1,.05,1),a12=slider(-1,1,.05,1),a21=slider(-1,1,.05,0),a22=slider(-1,1,.05,1),ofs= ('offset image from domain',False)): rf_low = RealField(12) my_mat = matrix(rf_low,2,2,[a11,a12,a21,a22]) u,s,vh = lin.svd(my_mat.numpy()) if ofs: offset = 3 fsize = 6 colors = [(1,0,0),(0,0,1),(1,0,0),(0,0,1)] else: offset = 0 fsize = 5 colors = [(1,0,0),(0,0,1),(.7,.2,0),(0,.3,.7)] vvects = sum([arrow([0,0],matrix(vh).row(i),rgbcolor = colors[i]) for i in (0,1)]) uvects = Graphics() for i in (0,1): if s[i] != 0: uvects += arrow([offset,0],vector([offset,0])+matrix(s*u).column(i),rgbcolor = colors[i+2]) pretty_print(html('<h3>Singular value decomposition: image of the unit circle and the singular vectors</h3>')) pretty_print(html("$A = %s = %s %s %s$"%(latex(my_mat), latex(matrix(rf_low,u.tolist())), latex(matrix(rf_low,2,2,[s[0],0,0,s[1]])), latex(matrix(rf_low,vh.tolist()))))) image_ell = parametric_plot(rotell(s,u,t, offset),(0,2*pi)) graph_stuff=circle((0,0),1)+image_ell+vvects+uvects graph_stuff.set_aspect_ratio(1) show(graph_stuff,frame = False,axes=False,figsize=[fsize,fsize])
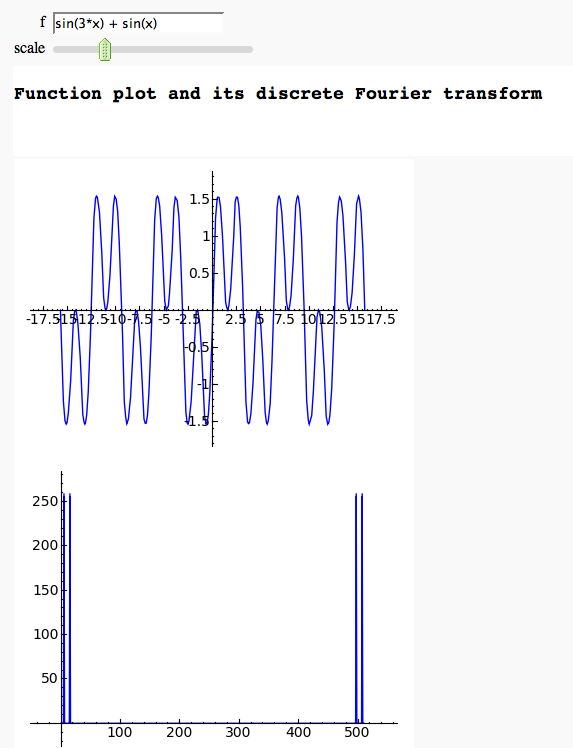
Discrete Fourier Transform
by Marshall Hampton
xxxxxxxxxximport scipy.fftpack as Fourierdef discrete_fourier(f = input_box(default=sum([sin(k*x) for k in range(1,5,2)])), scale = slider(.1,20,.1,5)): pbegin = -float(pi)*scale pend = float(pi)*scale pretty_print(html("<h3>Function plot and its discrete Fourier transform</h3>")) show(plot(f, (x,pbegin, pend), plot_points = 512), figsize = [4,3]) f_vals = [f(x=ind) for ind in srange(pbegin, pend,(pend-pbegin)/512.0)] my_fft = Fourier.fft(f_vals) show(list_plot([abs(i) for i in my_fft], plotjoined=True), figsize = [4,3])
The Gauss-Jordan method for inverting a matrix
by Hristo Inouzhe
xxxxxxxxxx#Choose the size D of the square matrix:D = 3example = [[1 if k==j else 0 for k in range(D)] for j in range(D)]example[0][-1] = 2example[-1][0] = 3def _(M=input_grid(D,D, default = example, label='Matrix to invert', to_value=matrix), tt = text_control('Enter the bits of precision used' ' (only if you entered floating point numbers)'), precision = slider(5,100,5,20), auto_update=False): if det(M)==0: print 'Failure: Matrix is not invertible' return if M.base_ring() == RR: M = M.apply_map(RealField(precision)) N=M M=M.augment(identity_matrix(D)) print 'We construct the augmented matrix' show(M) for m in range(0,D-1): if M[m,m] == 0: lista = [(abs(M[j,m]),j) for j in range(m+1,D)] maxi, c = max(lista) M[c,:],M[m,:]=M[m,:],M[c,:] print 'We permute rows %d and %d'%(m+1,c+1) show(M) for n in range(m+1,D): a=M[m,m] if M[n,m]!=0: print "We add %s times row %d to row %d"%(-M[n,m]/a, m+1, n+1) M=M.with_added_multiple_of_row(n,m,-M[n,m]/a) show(M) for m in range(D-1,-1,-1): for n in range(m-1,-1,-1): a=M[m,m] if M[n,m]!=0: print "We add %s times row %d to the row %d"%(-M[n,m]/a, m+1, n+1) M=M.with_added_multiple_of_row(n,m,-M[n,m]/a) show(M) for m in range(0,D): if M[m,m]!=1: print 'We divide row %d by %s'%(m+1,M[m,m]) M = M.with_row_set_to_multiple_of_row(m,m,1/M[m,m]) show(M) M=M.submatrix(0,D,D) print 'We keep the right submatrix, which contains the inverse' html('$$M^{-1}=%s$$'%latex(M)) print 'We check it actually is the inverse' html('$$M^{-1}*M=%s*%s=%s$$'%(latex(M),latex(N),latex(M*N)))
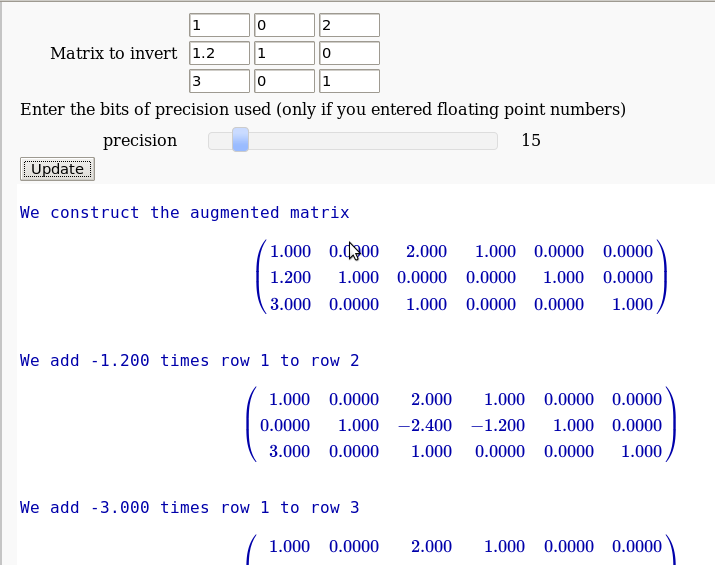
...(goes all the way to invert the matrix)
Solution of an homogeneous system of linear equations
by Pablo Angulo and Hristo Inouzhe
Coefficients are introduced as a matrix in a single text box. The number of equations and unknowns are arbitrary.
xxxxxxxxxxfrom sage.misc.html import HtmlFragmentdef HSLE_as_latex(A, variables): nvars = A.ncols() pretty_print(HtmlFragment( r'$$\left\{\begin{array}{%s}'%('r'*(nvars+1))+ r'\\'.join('%s=&0'%( ' & '.join((r'%s%s\cdot %s'%('+' if c>0 else '',c,v) if c else '') for c,v in zip(row, variables)) if not row.is_zero() else '&'*(nvars-1)+'0' ) for row in A)+ r'\end{array}\right.$$'))def SEL(A='[(0,1,-1,2),(-1,0,2,4), (0,-1,1,-2)]', auto_update=False ): M = A = matrix(eval(A)) neqs = M.nrows() nvars = M.ncols() var_names = ','.join('x%d'%j for j in [1..nvars]) variables = var(var_names) HSLE_as_latex(M, variables) pretty_print(HtmlFragment( 'SEL in matrix form')) show(M) pivot = {} ibound_variables = [] for m,row in enumerate(M): for k in range(m,nvars): lista = [(abs(M[j,k]),j) for j in range(m,neqs)] maxi, c = max(lista) if maxi > 0: ibound_variables.append(k) if M[m,k]==0: M[c,:],M[m,:]=M[m,:],M[c,:] pretty_print( HtmlFragment('We permute rows %d and %d'%(m+1,c+1))) show(M) pivot[m] = k break a=M[m,k] for n in range(m+1,neqs): if M[n,k]!=0: pretty_print( HtmlFragment("We add %s times row %d to row %d"%(-M[n,k]/a, m+1, n+1))) M=M.with_added_multiple_of_row(n,m,-M[n,k]/a) show(M) pretty_print( HtmlFragment('Equivalent system of equations')) HSLE_as_latex(M, variables) SEL_type = 'compatible' null_rows = None for k,row in enumerate(M): if row.is_zero(): pretty_print( HtmlFragment('We remove trivial 0=0 equations')) M = M[:k,:] HSLE_as_latex(M, variables) ifree_variables = [k for k in range(nvars) if k not in ibound_variables] bound_variables = [variables[k] for k in ibound_variables] free_variables = [variables[k] for k in ifree_variables] pretty_print( HtmlFragment('Free variables: %s'% free_variables)) pretty_print( HtmlFragment('Bound variables: %s'% bound_variables)) reduced_eqs = [ sum(c*v for c,v in zip(row, variables))==0 for row in M ] xvector = vector(variables) if len(bound_variables)==1: soldict = solve(reduced_eqs, bound_variables[0], solution_dict=True)[0] else: soldict = solve(reduced_eqs, bound_variables, solution_dict=True)[0] pretty_print( HtmlFragment('Solution in parametric form')) parametric_sol = matrix( xvector.apply_map(lambda s:s.subs(soldict)) ).transpose() show(parametric_sol) pretty_print( HtmlFragment('Generators')) pretty_print( HtmlFragment( r'$$\langle %s\rangle$$'%','.join(latex( parametric_sol.subs(dict((variables[k],1 if j==k else 0) for k in ifree_variables)) ) for j in ifree_variables) )) pretty_print( HtmlFragment('Dimension is %d'%len(free_variables)))
Solution of a non homogeneous system of linear equations
by Pablo Angulo and Hristo Inouzhe
Coefficients are introduced as a matrix in a single text box, and independent terms as a vector in a separate text box. The number of equations and unknowns are arbitrary.
xxxxxxxxxxfrom sage.misc.html import HtmlFragmentdef SLE_as_latex(A, b, variables): nvars = A.ncols() pretty_print(HtmlFragment( r'$$\left\{\begin{array}{%s}'%('r'*(nvars+1))+ r'\\'.join('%s=&%s'%( (' & '.join((r'%s%s\cdot %s'%('+' if c>0 else '',c,v) if c else '') for c,v in zip(row, variables)) if not row.is_zero() else '&'*(nvars-1)+'0',y) ) for row,y in zip(A,b))+ r'\end{array}\right.$$'))def extended_matrix_as_latex(M): A = M[:,:-1] b = M.column(-1) nvars = A.ncols() pretty_print(HtmlFragment( r'$$\left(\begin{array}{%s}'%('r'*nvars+ '|r')+ r'\\'.join('%s&%s'%( ' & '.join('%s'%c for c in row) ,y) for row,y in zip(A,b))+ r'\end{array}\right)$$'))def SEL(A_text='[(0,0,-1,2),(-1,0,2,4), (0,0,1,-2)]', b_text='[2,1,-2]', auto_update=False ): A = matrix(eval(A_text)) b = vector(eval(b_text)) M = A.augment(b) neqs = len(b) nvars = A.ncols() var_names = ','.join('x%d'%j for j in [1..nvars]) variables = var(var_names) pretty_print(HtmlFragment('Variables: %s'% var_names)) for row,y in zip(A,b): pretty_print(HtmlFragment(sum(c*v for c,v in zip(row, variables))==y)) SLE_as_latex(A, b, variables) pretty_print(HtmlFragment( 'We construct the augmented matrix')) extended_matrix_as_latex(M) pivot = {} ibound_variables = [] for m,row in enumerate(A): for k in range(m,nvars): lista = [(abs(M[j,k]),j) for j in range(m,neqs)] maxi, c = max(lista) if maxi > 0: ibound_variables.append(k) if M[m,k]==0: M[c,:],M[m,:]=M[m,:],M[c,:] pretty_print( HtmlFragment('We permute rows %d and %d'%(m+1,c+1))) extended_matrix_as_latex(M) pivot[m] = k break a=M[m,k] for n in range(m+1,neqs): if M[n,k]!=0: pretty_print( HtmlFragment("We add %s times row %d to row %d"%(-M[n,k]/a, m+1, n+1))) M=M.with_added_multiple_of_row(n,m,-M[n,k]/a) extended_matrix_as_latex(M) A = M[:,:-1] b = M.column(-1) SLE_as_latex(A, b, variables) SEL_type = 'compatible' null_rows = None for k,(row,y) in enumerate(zip(A,b)): if row.is_zero(): if y==0 and null_rows is None: null_rows = k break elif y!=0: SEL_type = 'incompatible' if SEL_type == 'incompatible': pretty_print( HtmlFragment('The system has no solutions')) return if null_rows: pretty_print(HtmlFragment('We remove trivial 0=0 equations')) A = A[:null_rows,:] b = b[:null_rows] SLE_as_latex(A, b, variables) ifree_variables = [k for k in range(nvars) if k not in ibound_variables] bound_variables = [variables[k] for k in ibound_variables] free_variables = [variables[k] for k in ifree_variables] pretty_print( HtmlFragment('Free variables: %s'% free_variables)) pretty_print( HtmlFragment('Bound variables: %s'% bound_variables)) reduced_eqs = [ sum(c*v for c,v in zip(row, variables))==y for row,y in zip(A,b) ] xvector = vector(variables) if len(bound_variables)==1: soldict = solve(reduced_eqs, bound_variables[0], solution_dict=True)[0] else: soldict = solve(reduced_eqs, bound_variables, solution_dict=True)[0] pretty_print( HtmlFragment('Solution in parametric form')) parametric_sol = matrix( xvector.apply_map(lambda s:s.subs(soldict)) ).transpose() show(parametric_sol) pretty_print( HtmlFragment('Solution in vector form')) pretty_print( HtmlFragment( r'$$ %s + \left\langle %s\right\rangle$$'%( latex(parametric_sol.subs(dict(zip(free_variables, [0]*len(free_variables))))), ','.join(latex( parametric_sol.apply_map(lambda s:s.diff(v)) ) for v in free_variables) if free_variables else latex(matrix([0]*nvars).transpose())) )) pretty_print( HtmlFragment('Dimension is %d'%len(free_variables)))
