Cauchy residue theorem
Pablo Angulo. Shows a function f of a complex variable, a plane curve gamma given as a map R -> C t -> gamma(t) and plots the contribution of the residues of f to the contour integral of f along gamma
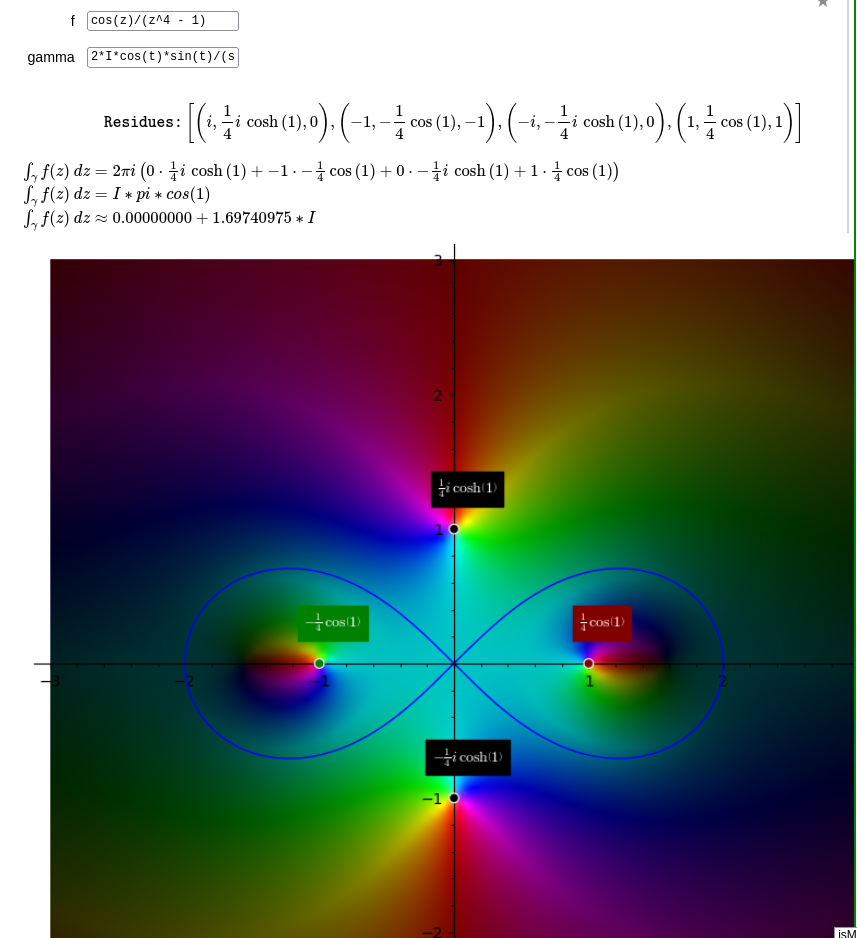
Pablo Angulo. Shows a function f of a complex variable, a plane curve gamma given as a map R -> C t -> gamma(t) and plots the contribution of the residues of f to the contour integral of f along gamma

interact/complex (last edited 2021-06-24 22:30:22 by pang)