For code, see http://trac.sagemath.org/sage_trac/ticket/174
Fast Hermite Normal Form over ZZ
We did it! Get hnf.hg from here http://trac.sagemath.org/sage_trac/ticket/174
Status Report
Unless otherwise stated, all benchmarks below were done on a 2.6Ghz core 2 duo laptop running OS X and 32-bit Sage and 32-bit Magma.
STATUS REPORT:
Modular / p-adic HNF algorithm -- Stein, Pernet, Burcin
"Magma V2.13 (now released) has an implementation of a new modular
algorithm for computing the Hermite Normal Form of an integer
matrix. On this page I compare this with other implementations.
[See timings below where Magma is VASTLY faster then every
other program in existence.]"
-- Allan SteelAnother example with big coefficients (which is what I -- Stein -- care about):
sage: a = random_matrix(ZZ,100, x=-2^32, y=2^32)
sage: time v = a._hnf()
CPU times: user 0.41 s, sys: 0.03 s, total: 0.43 s
Wall time: 0.44
sage: set_verbose(1)which sure beats Sage right now:
sage: time b = a.echelon_form()
CPU times: user 16.57 s, sys: 0.11 s, total: 16.68 s
Wall time: 16.92and even beats Magma too:
sage: m = magma(a)
sage: t = magma.cputime(); b = m.EchelonForm(); magma.cputime(t)
1.26
Try 200x200 over ZZ with small coeffs with PARI, Magma, Sage
dhcp46-76:hnf was$ sage ---------------------------------------------------------------------- | SAGE Version 2.10.1, Release Date: 2008-02-02 | | Type notebook() for the GUI, and license() for information. | ---------------------------------------------------------------------- Loading SAGE library. Current Mercurial branch is: abelian_rewrite sage: a = random_matrix(ZZ,200) sage: time e = a.echelon_form() CPU times: user 43.51 s, sys: 0.41 s, total: 43.93 s Wall time: 48.67 sage: time e = a._hn a._hnf a._hnf_mod sage: time e = a._hnf() CPU times: user 0.97 s, sys: 0.08 s, total: 1.05 s Wall time: 1.27 sage: set_verbose(1) sage: set_verbose(0) sage: set_verbose(1) sage: time e = a._hnf() verbose 1 (194: matrix_integer_dense_hnf.py, hnf) starting slicings verbose 1 (194: matrix_integer_dense_hnf.py, hnf) done slicing (time = 0.033891) verbose 1 (59: matrix_integer_dense_hnf.py, doubleDet) starting double det verbose 1 (59: matrix_integer_dense_hnf.py, doubleDet) starting linbox solve_right... verbose 1 (59: matrix_integer_dense_hnf.py, doubleDet) finished solve_right (time = 0.128766) verbose 1 (59: matrix_integer_dense_hnf.py, doubleDet) _charpoly_linbox... verbose 1 (59: matrix_integer_dense_hnf.py, doubleDet) _charpoly_linbox... verbose 1 (59: matrix_integer_dense_hnf.py, doubleDet) finished double det (time = 0.243717) verbose 1 (194: matrix_integer_dense_hnf.py, matrix_integer_dense) hermite mod 58 verbose 1 (194: matrix_integer_dense_hnf.py, matrix_integer_dense) finished hnf mod (time = 0.125313) verbose 1 (112: matrix_integer_dense_hnf.py, add_column) starting add_column verbose 1 (112: matrix_integer_dense_hnf.py, add_column) starting linbox solve_right... verbose 1 (112: matrix_integer_dense_hnf.py, add_column) finished solve_right (time = 0.168505) verbose 1 (112: matrix_integer_dense_hnf.py, add_column) computing nullspace of 198 x 199 matrix using IML verbose 1 (112: matrix_integer_dense_hnf.py, add_column) finished computing nullspace (time = 0.154126) verbose 1 (174: matrix_integer_dense_hnf.py, add_row) first add row verbose 1 (174: matrix_integer_dense_hnf.py, add_row) finished add row (time = 0.059144) verbose 1 (174: matrix_integer_dense_hnf.py, add_row) first add row verbose 1 (174: matrix_integer_dense_hnf.py, add_row) finished add row (time = 0.10742) CPU times: user 0.96 s, sys: 0.08 s, total: 1.05 s Wall time: 1.04
Todo
- more rows than columns
- more columns than rows
- degenerate cases -- fail nicely
- provably correct determinant (via linbox)
- transition matrix
- memory leaks?!
- Make this the default in Sage.
- improve documentation
- testing for correctness
- generalize to polynomials
- write a "technical report" with tables of timings
A few Misc Benchmarks of Existing Code (before this sprint)
Unless otherwise stated benchmarks are on OS X 2.6Ghz core 2 duo laptop.
Comparing Magma (red) and Sage (blue)
Random n x n matrix.
Vertical Axis = coefficient bitsize
Horizontal Axis = n.
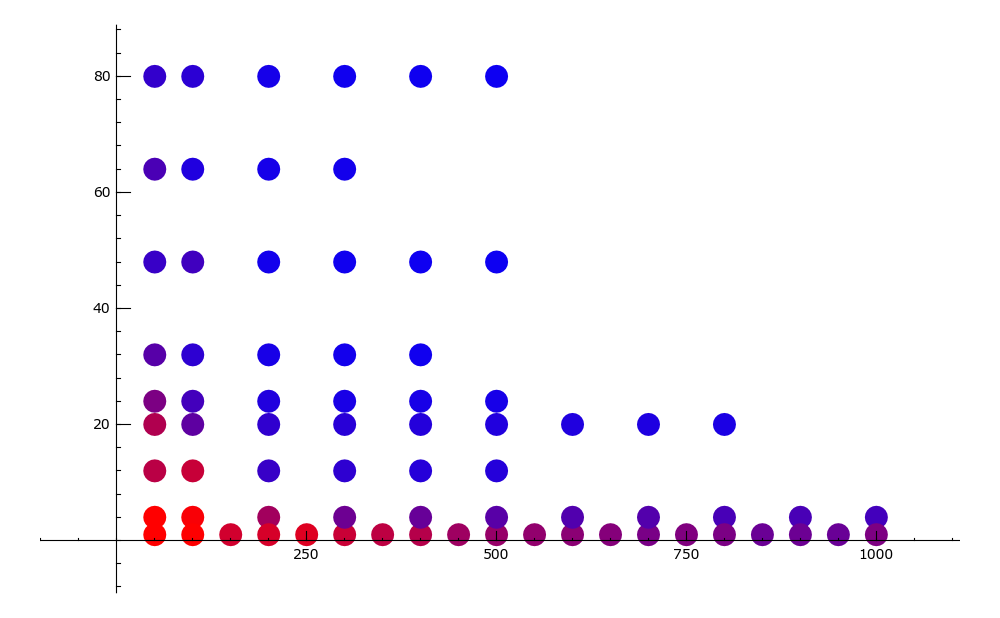
Comparing Magma (red) and Sage (blue): 4-bit entries
Random n x n matrix.
Vertical Axis = time in seconds
Horizontal Axis = n.
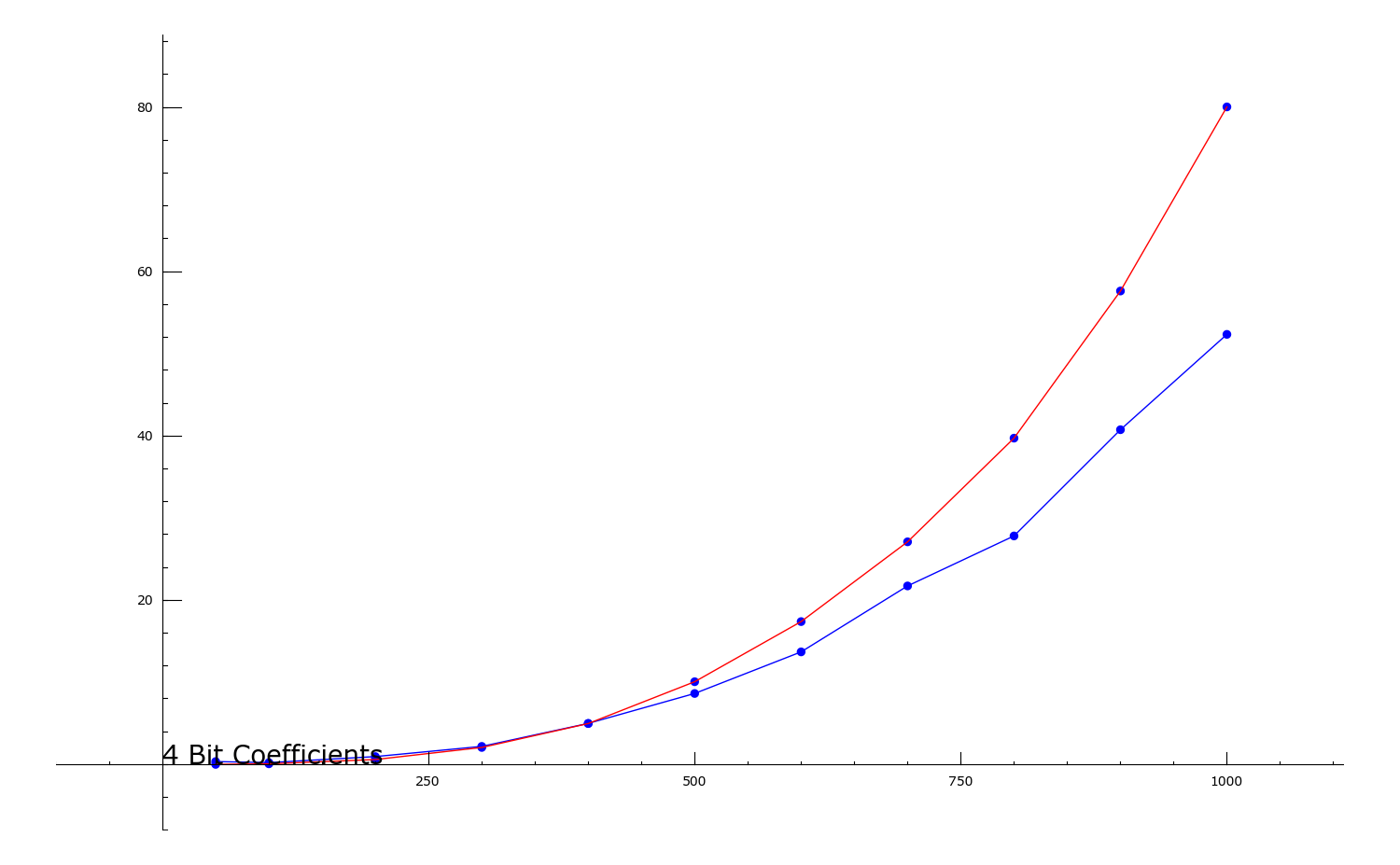
Comparing Magma (red) and Sage (blue): 20-bit entries
Random n x n matrix.
Vertical Axis = time in seconds
Horizontal Axis = n.
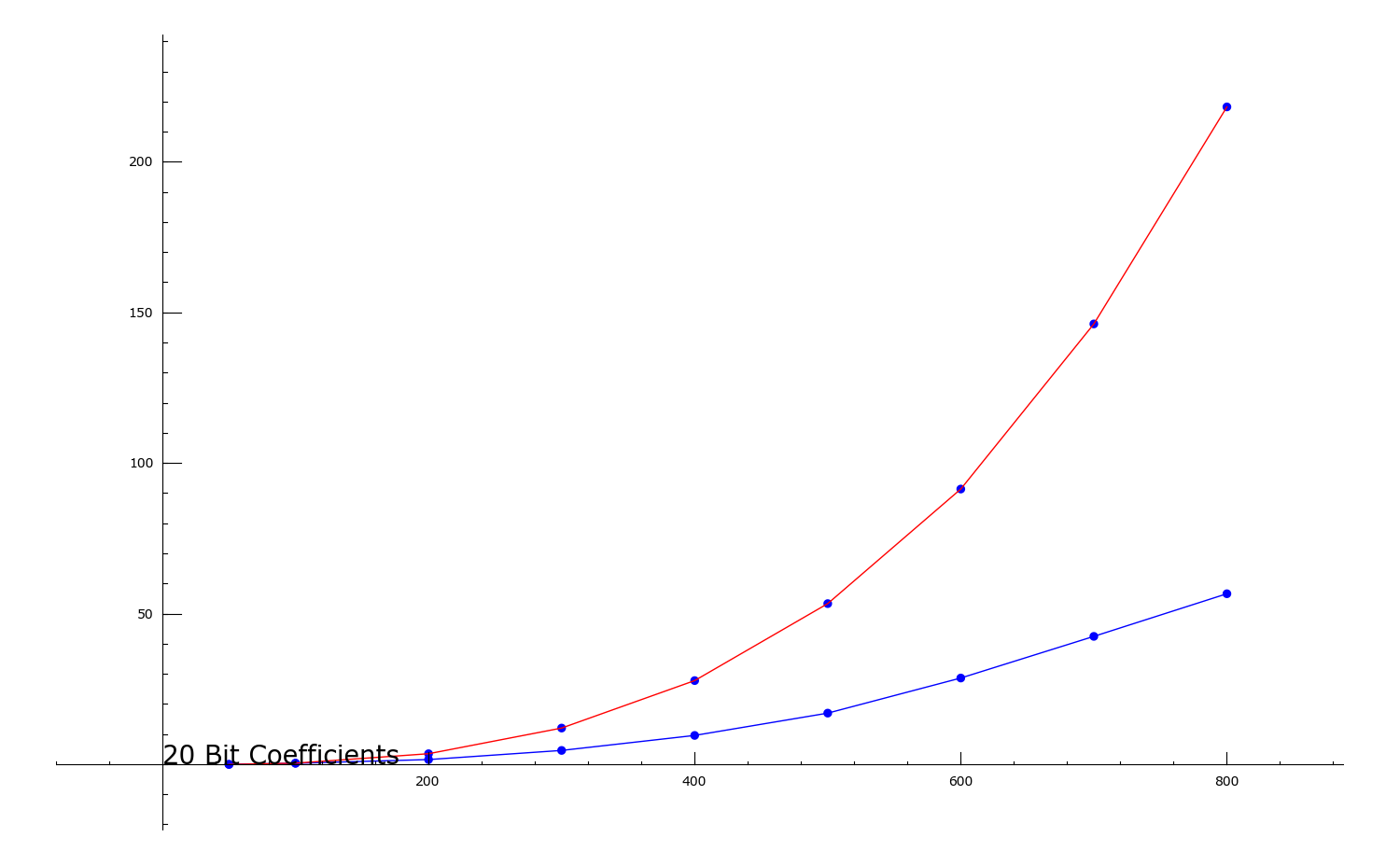
Comparing Magma (red) and Sage (blue): 64-bit entries
Random n x n matrix.
Vertical Axis = time in seconds
Horizontal Axis = n.
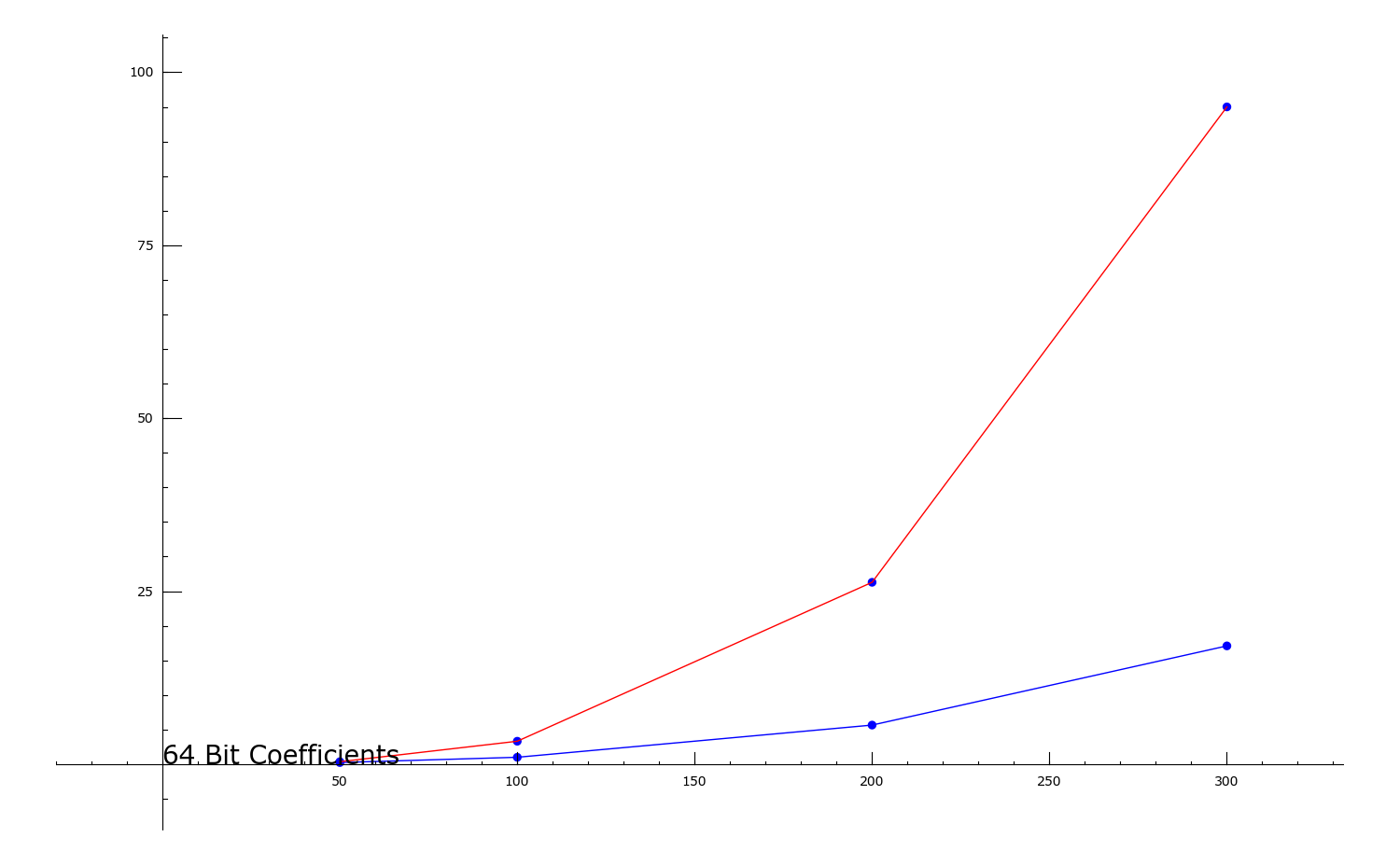
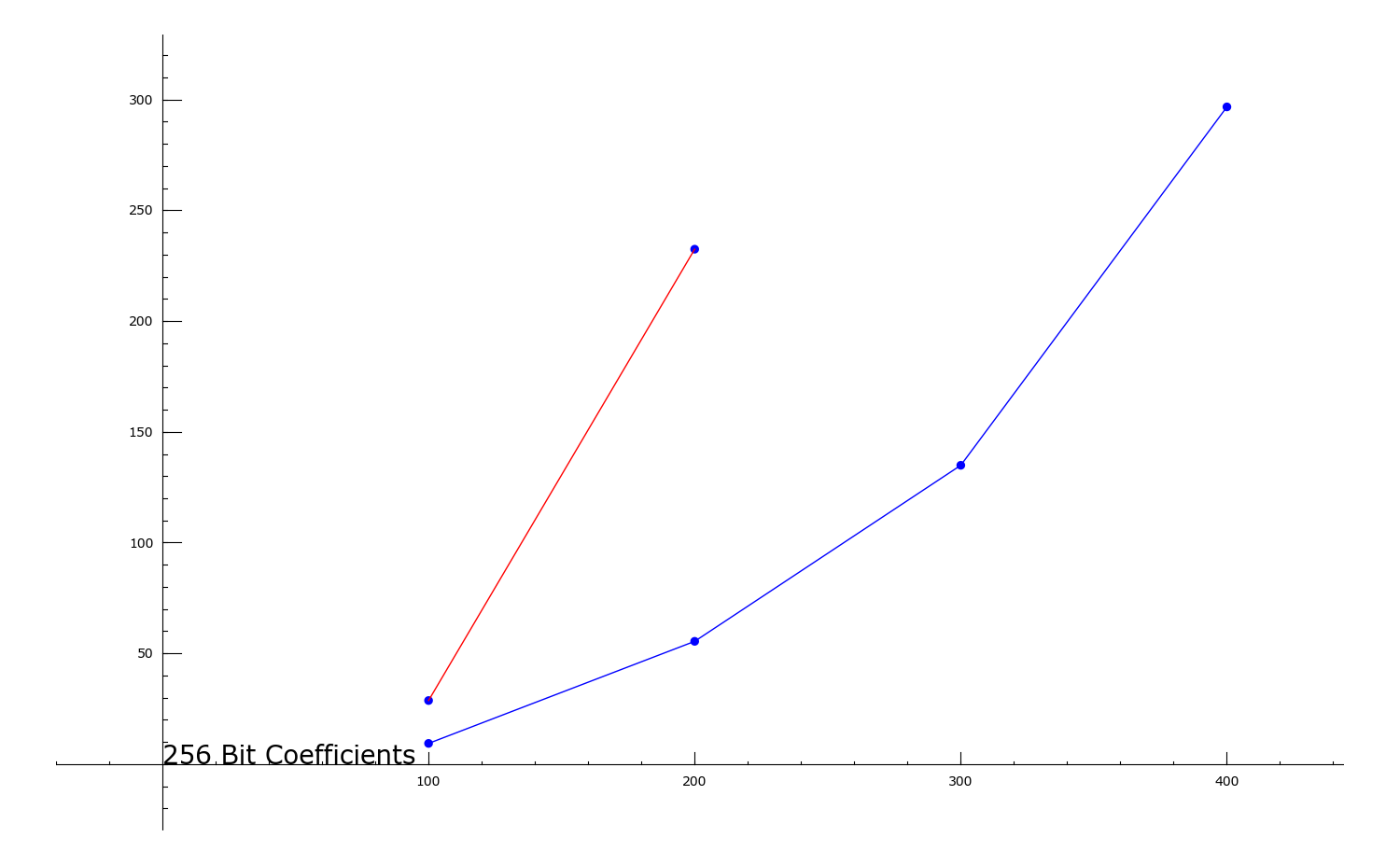
Comparing Magma (red) and Sage (blue): 256-bit entries
Random n x n matrix.
Vertical Axis = time in seconds
Horizontal Axis = n.
(the last magma timing would take about an hour so I gave up)
Benchmark 1: Random 50x50 single-digit matrix
MuPAD
>> A := linalg::randomMatrix(50,50,Dom::Integer, 10);
Warning: This matrix is too large for display. If you want to see all non-zero entries of large matrices, use doprint(..). [(Dom::Matrix(Dom::Integer))::print]
Dom::Matrix(Dom::Integer)(50, 50, ["..."])
>> time(linalg::hermiteForm(A));
26445
Benchmark 1: Random 200x200 single-digit matrix
Mathematica code:
sage: mathematica.eval('a = Table[RandomInteger[{0,9}], {i,200}, {j,200}];')
sage: mathematica.eval('Timing[HermiteDecomposition[a];]')
{98.9791, Null}Maple code:
> with(LinearAlgebra); n := 200: k := 9: A := RandomMatrix(n,n,generator=rand(-k..k)): time( HermiteForm(A,output=['H', 'U']) ); 60.431 seconds
Sage (via PARI):
sage: a = random_matrix(ZZ,200) sage: time v = a.echelon_form() CPU times: user 43.72 s, sys: 0.27 s, total: 43.98 s Wall time: 44.36
Sage (via NTL):
sage: a = random_matrix(ZZ,200, x=-9, y=9) sage: time e = a.echelon_form(algorithm='ntl') CPU times: user 26.11 s, sys: 0.27 s, total: 26.38 s Wall time: 35.52
sage: a = random_matrix(ZZ,200) sage: z = magma(a) sage: t = magma.cputime() sage: time w = z.HermiteForm() CPU times: user 0.00 s, sys: 0.00 s, total: 0.00 s Wall time: 0.82 sage: magma.cputime(t) 0.68999999999999995
Benchmark 1: Random 200x200 matrix with 32-bit entries
Maple (on mhansen's laptop):
> with(LinearAlgebra); n := 200: k := 2147483646: A := RandomMatrix(n,n,generator=rand(-k..k)): time( HermiteForm(A,output=['H', 'U']) ); 336.753seconds
NTL
sage: a = random_matrix(ZZ, 200, x=-2^32, y=2^32) sage: time e = a.echelon_form(algorithm='ntl') CPU times: user 461.25 s, sys: 2.71 s, total: 463.97 s
PARI
sage: a = random_matrix(ZZ, 200, x=-2^32, y=2^32) sage: time e = a.echelon_form(algorithm='pari') CPU times: user 466.90 s, sys: 12.86 s, total: 479.76 s
MAGMA (amazingly fast):
sage: a = random_matrix(ZZ,200,x=-2^32,y=2^32) sage: m = magma(a) sage: t = magma.cputime() sage: w = m.HermiteForm() sage: magma.cputime(t) 10.33
MATHEMATICA (shockingly slow!):
sage: mathematica.eval('a = Table[RandomInteger[{-2^32,2^32}], {i,200}, {j,200}];')
sage: time mathematica.eval('Timing[HermiteDecomposition[a];]')
CPU times: user 0.00 s, sys: 0.00 s, total: 0.00 s
Wall time: 1376.37
{1366.7, Null}