Multiple Zeta Values

by Akhilesh P.

Computing Multiple Zeta values (Euler-Zagier numbers)

Word Input

akhi1.png

Composition Input

akhi5.png

Program to Compute Integer Relation between Multiple Zeta Values (Euler-Zagier numbers)

akhi10.png

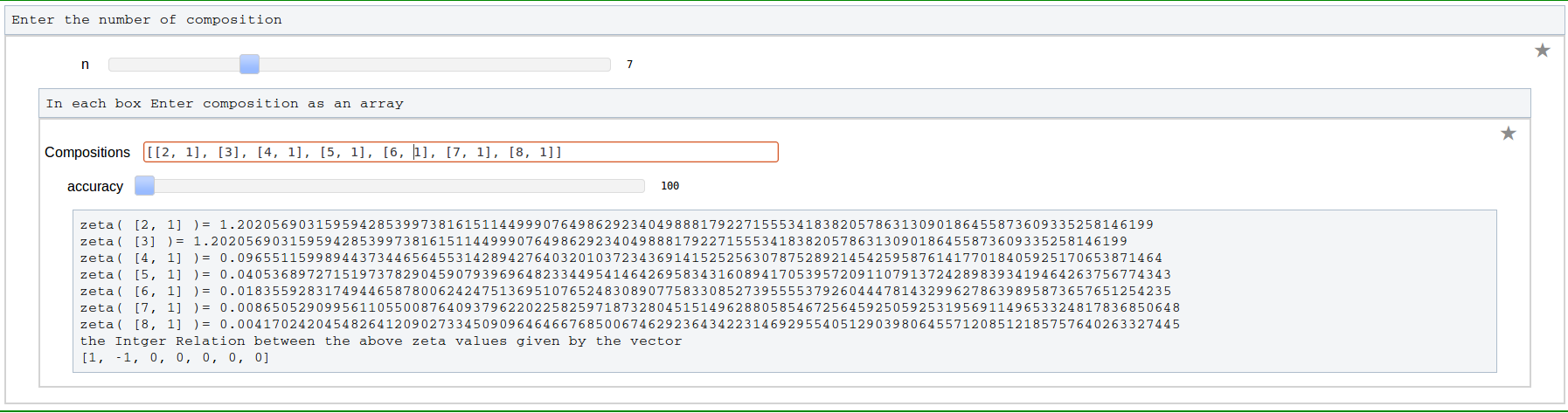
Word to composition

akhi2.png

Composition to Word

akhi3.png

Dual of a Word

akhi4.png

Shuffle product of two Words

akhi6.png

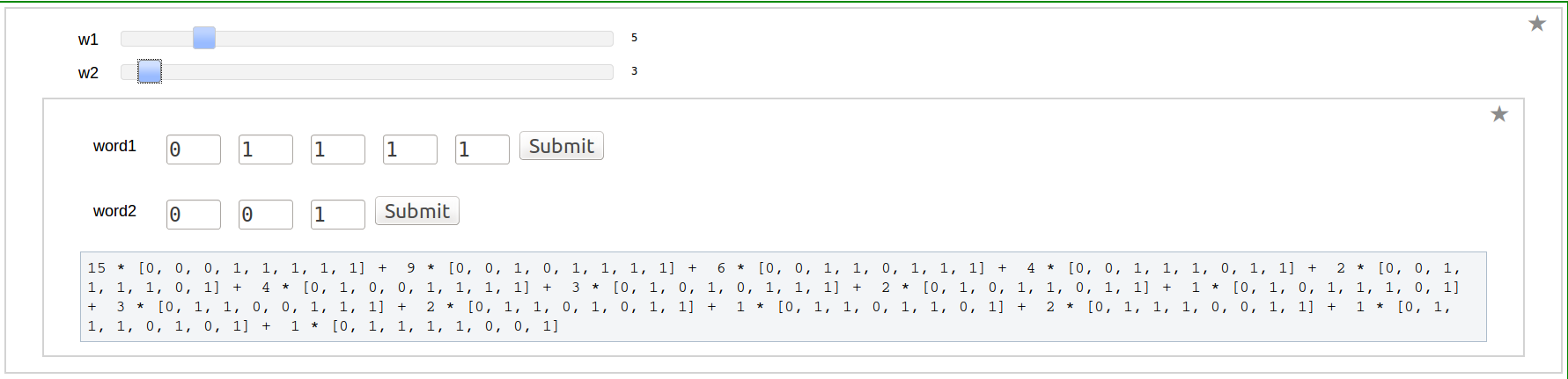
Shuffle Regularization at 0

akhi7.png

Shuffle Regularization at 1

akhi8.png

interact/number_theory/Multiple Zeta Values (last edited 2016-05-09 09:54:38 by akhi)