Sage Interactions - Miscellaneous
goto interact main page
Contents
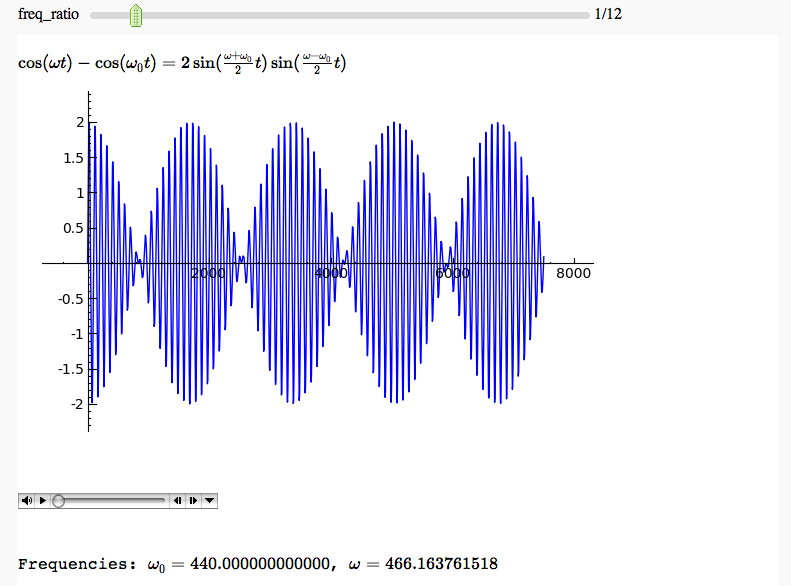
Hearing a trigonometric identity
by Marshall Hampton. When the two frequencies are well separated, we hear the right hand side of the identity. When they start getting close, we hear the higher-pitched factor in the left-hand side modulated by the lower-pitched envelope.
xxxxxxxxxximport waveclass SoundFile: def __init__(self, signal,lab=''): self.file = wave.open('./test' + lab + '.wav', 'wb') self.signal = signal self.sr = 44100 def write(self): self.file.setparams((1, 2, self.sr, 44100*4, 'NONE', 'noncompressed')) self.file.writeframes(self.signal) self.file.close()mypi = float(pi)from math import sindef sinsound(freq_ratio = slider(1/144,1,1/144,1/12)): hz1 = 440.0 hz2 = float(440.0*2^freq_ratio) html('$\cos(\omega t) - \cos(\omega_0 t) = 2 \sin(\\frac{\omega + \omega_0}{2}t) \sin(\\frac{\omega - \omega_0}{2}t)$') s2 = [sin(hz1*x*mypi*2)+sin(hz2*x*mypi*2) for x in srange(0,4,1/44100.0)] s2m = max(s2) s2f = [16384*x/s2m for x in s2] s2str = ''.join(wave.struct.pack('h',x) for x in s2f) lab="%1.2f"%float(freq_ratio) f = SoundFile(s2str,lab=lab) f.write() pnum = 1500+int(500/freq_ratio) show(list_plot(s2[0:pnum],plotjoined=True)) html('<embed src="cell://test'+ lab +'.wav" width="200" height="100"></embed>') html('Frequencies: '+ '$\omega_0 = ' + str(hz1) + ' $, $\omega = '+latex(hz2) + '$')
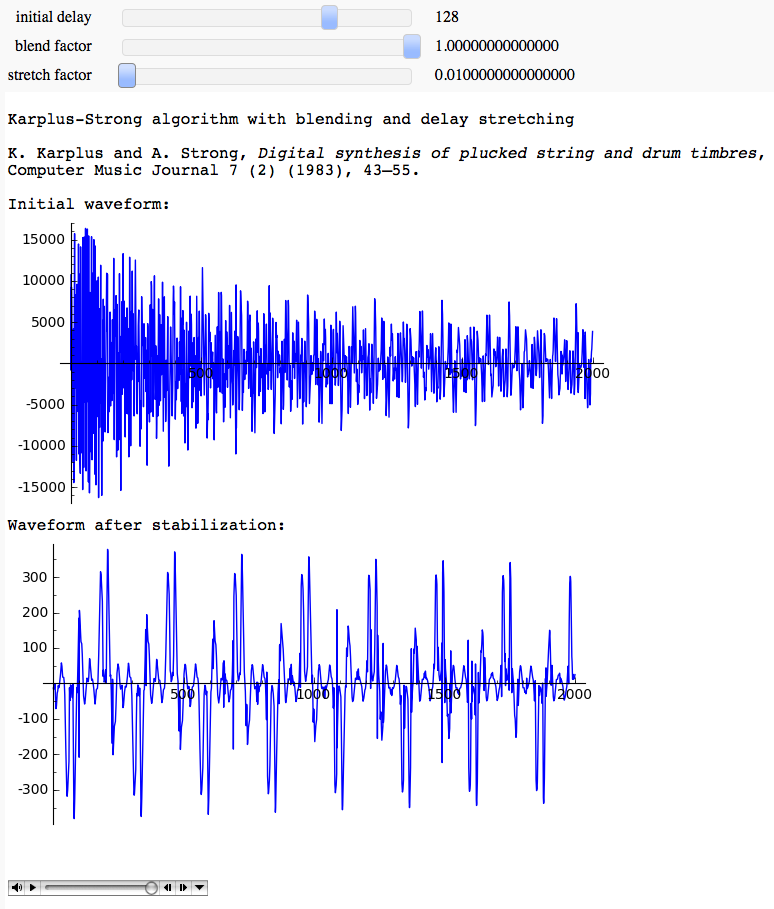
Karplus-Strong algorithm for plucked and percussive sound generation
by Marshall Hampton
xxxxxxxxxximport waveclass SoundFile: def __init__(self, signal,lab=''): self.file = wave.open('./test' + lab + '.wav', 'wb') self.signal = signal self.sr = 44100 def write(self): self.file.setparams((1, 2, self.sr, 44100*4, 'NONE', 'noncompressed')) self.file.writeframes(self.signal) self.file.close()mypi = float(pi)from math import sindef ks(delay,length,blend = 0,filler=None,stretch=0): if filler == None: filler = [randint(-16383,16383) for q in range(delay+1)] outsig = filler[:] index = len(filler) while len(outsig) < length: s = random() if s > stretch: b = random() if b < 1-blend: newvalue = (outsig[index-delay]+outsig[index-delay-1])*.5 else: newvalue = -(outsig[index-delay]+outsig[index-delay-1])*.5 else: newvalue = outsig[index-delay] outsig.append(newvalue) index += 1 return [int(round(x)) for x in outsig]def sinsound(delay = slider([int(2^i) for i in range(2,10)], default=100, label="initial delay"), blend=slider(srange(0,1,.01,include_endpoint=True),default=0,label="blend factor"), stretch=slider(srange(0,1,.01,include_endpoint=True),default=0,label="stretch factor")): s2f = ks(delay,int(44100*(1/2)),blend=blend,stretch=stretch) for i in range(12): s2f = s2f + ks(int(2^((12+i)/12.0)*delay),int(44100*(1/2)),blend=blend, stretch=stretch) html("Karplus-Strong algorithm with blending and delay stretching") html("<br>K. Karplus and A. Strong, <em>Digital synthesis of plucked string and drum timbres</em>, \nComputer Music Journal 7 (2) (1983), 43–55.<br>") html("Initial waveform:") show(list_plot(s2f[0:2000],plotjoined=True), figsize = [7,3.5]) html("Waveform after stabilization:") show(list_plot(s2f[20000:22000],plotjoined=True), figsize = [7,3.5]) s2str = ''.join(wave.struct.pack('h',x) for x in s2f) lab="" f = SoundFile(s2str,lab=lab) f.write() html('<embed src="cell://test'+ lab +'.wav" width="200" height="100"></embed>')
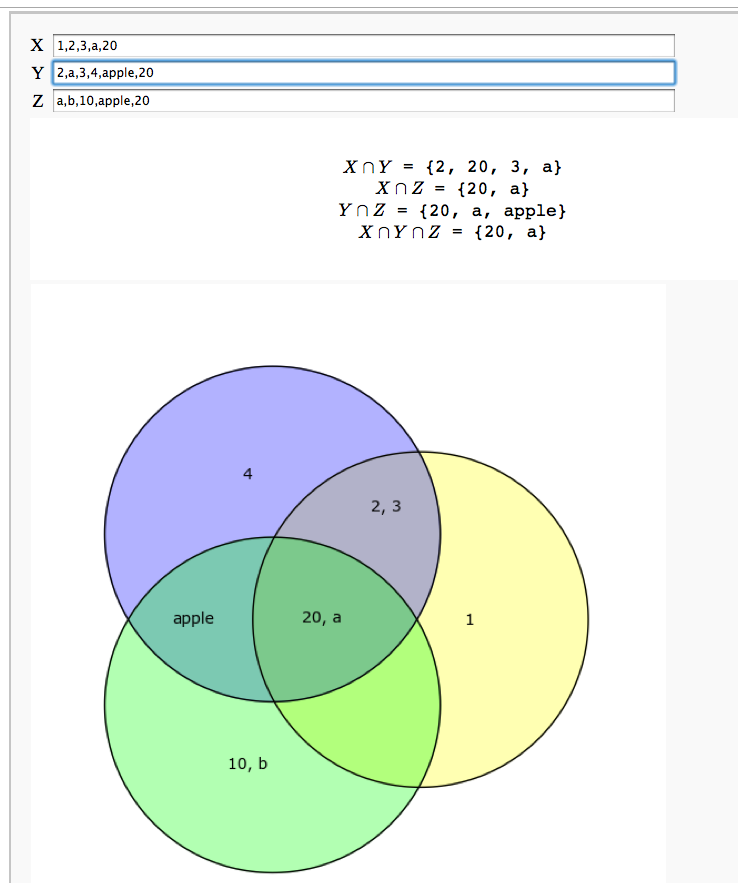
An Interactive Venn Diagram
xxxxxxxxxxdef f(s, braces=True): t = ', '.join(sorted(list(s))) if braces: return '{' + t + '}' return tdef g(s): return set(str(s).replace(',',' ').split())def _(X='1,2,3,a', Y='2,a,3,4,apple', Z='a,b,10,apple'): S = [g(X), g(Y), g(Z)] X,Y,Z = S XY = X & Y XZ = X & Z YZ = Y & Z XYZ = XY & Z html('<center>') html("$X \cap Y$ = %s"%f(XY)) html("$X \cap Z$ = %s"%f(XZ)) html("$Y \cap Z$ = %s"%f(YZ)) html("$X \cap Y \cap Z$ = %s"%f(XYZ)) html('</center>') centers = [(cos(n*2*pi/3), sin(n*2*pi/3)) for n in [0,1,2]] scale = 1.7 clr = ['yellow', 'blue', 'green'] G = Graphics() for i in range(len(S)): G += circle(centers[i], scale, rgbcolor=clr[i], fill=True, alpha=0.3) for i in range(len(S)): G += circle(centers[i], scale, rgbcolor='black') # Plot what is in one but neither other for i in range(len(S)): Z = set(S[i]) for j in range(1,len(S)): Z = Z.difference(S[(i+j)%3]) G += text(f(Z,braces=False), (1.5*centers[i][0],1.7*centers[i][1]), rgbcolor='black') # Plot pairs of intersections for i in range(len(S)): Z = (set(S[i]) & S[(i+1)%3]) - set(XYZ) C = (1.3*cos(i*2*pi/3 + pi/3), 1.3*sin(i*2*pi/3 + pi/3)) G += text(f(Z,braces=False), C, rgbcolor='black') # Plot intersection of all three G += text(f(XYZ,braces=False), (0,0), rgbcolor='black') # Show it G.show(aspect_ratio=1, axes=False)
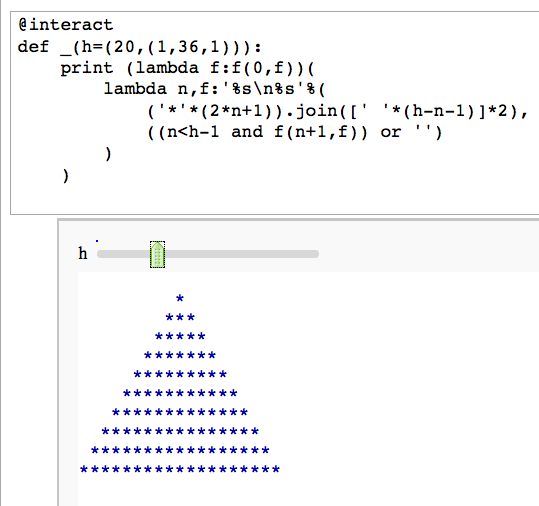
Unreadable code
by Igor Tolkov
xxxxxxxxxxdef _(h=(20,(1,36,1))): print (lambda f:f(0,f))( lambda n,f:'%s\n%s'%( ('*'*(2*n+1)).join([' '*(h-n-1)]*2), ((n<h-1 and f(n+1,f)) or '') ) )
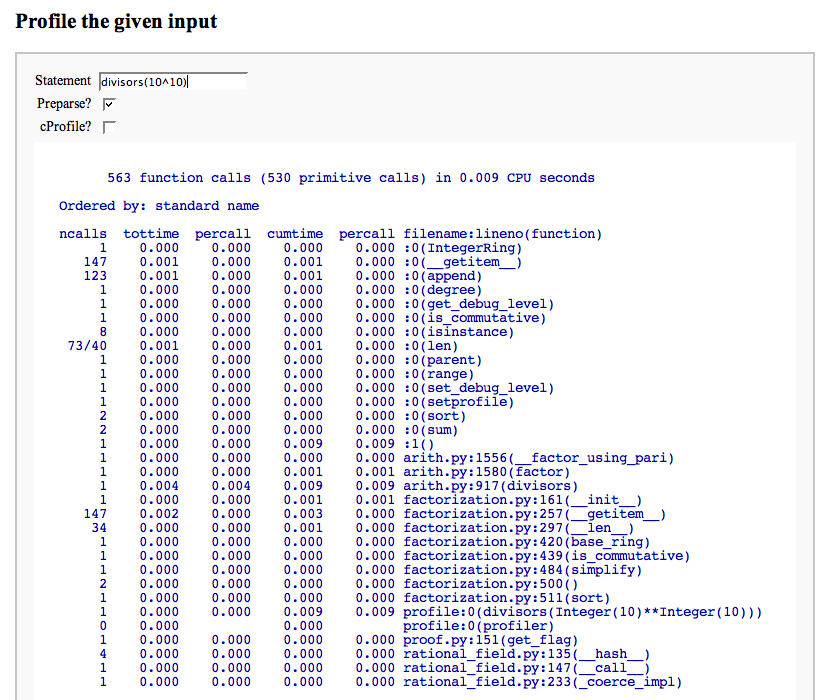
Profile a snippet of code
xxxxxxxxxxhtml('<h2>Profile the given input</h2>')import cProfile; import profiledef _(cmd = ("Statement", '2 + 2'), do_preparse=("Preparse?", True), cprof =("cProfile?", False)): if do_preparse: cmd = preparse(cmd) print "<html>" # trick to avoid word wrap if cprof: cProfile.run(cmd) else: profile.run(cmd) print "</html>"
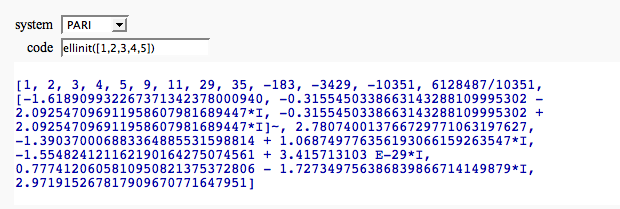
Evaluate a bit of code in a given system
by William Stein (there is no way yet to make the text box big):
xxxxxxxxxxdef _(system=selector([('sage0', 'Sage'), ('gp', 'PARI'), ('magma', 'Magma')]), code='2+2'): print globals()[system].eval(code)
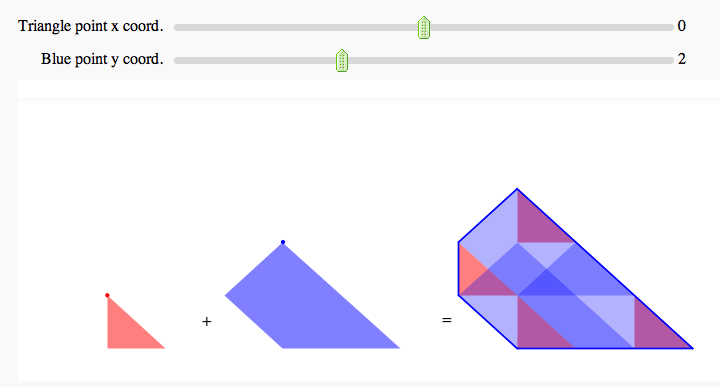
Minkowski Sum
by Marshall Hampton
xxxxxxxxxxdef minkdemo(list1,list2): ''' Returns the Minkowski sum of two lists. ''' output = [] for stuff1 in list1: for stuff2 in list2: temp = [stuff1[i] + stuff2[i] for i in range(len(stuff1))] output.append(temp) return outputdef minksumvis(x1tri = slider(-1,1,1/10,0, label = 'Triangle point x coord.'), yb = slider(1,4,1/10,2, label = 'Blue point y coord.')): t_list = [[1,0],[x1tri,1],[0,0]] kite_list = [[3, 0], [1, 0], [0, 1], [1, yb]] triangle = polygon([[q[0]-6,q[1]] for q in t_list], alpha = .5, rgbcolor = (1,0,0)) t_vert = point([x1tri-6,1], rgbcolor = (1,0,0)) b_vert = point([kite_list[3][0]-4,yb], rgbcolor = (0,0,1)) kite = polygon([[q[0]-4,q[1]] for q in kite_list], alpha = .5,rgbcolor = (0,0,1)) p12 = minkdemo(t_list, kite_list) p12 = [[q[0],q[1]] for q in p12] p12poly = Polyhedron(p12) edge_lines = Graphics() verts = p12poly.vertices() for an_edge in p12poly.vertex_adjacencies(): edge_lines += line([verts[an_edge[0]], verts[an_edge[1][0]]]) edge_lines += line([verts[an_edge[0]], verts[an_edge[1][1]]]) triangle_sum = Graphics() for vert in kite_list: temp_list = [] for q in t_list: temp_list.append([q[i] + vert[i] for i in range(len(t_list[0]))]) triangle_sum += polygon(temp_list, alpha = .5, rgbcolor = (1,0,0)) kite_sum = Graphics() for vert in t_list: temp_list = [] for q in kite_list: temp_list.append([q[i] + vert[i] for i in range(len(t_list[0]))]) kite_sum += polygon(temp_list, alpha = .3,rgbcolor = (0,0,1)) labels = text('+', (-4.3,.5), rgbcolor = (0,0,0)) labels += text('=', (-.2,.5), rgbcolor = (0,0,0)) show(labels + t_vert + b_vert+ triangle + kite + triangle_sum + kite_sum + edge_lines, axes=False, figsize = [11.0*.7, 4*.7], xmin = -6, ymin = 0, ymax = 4)
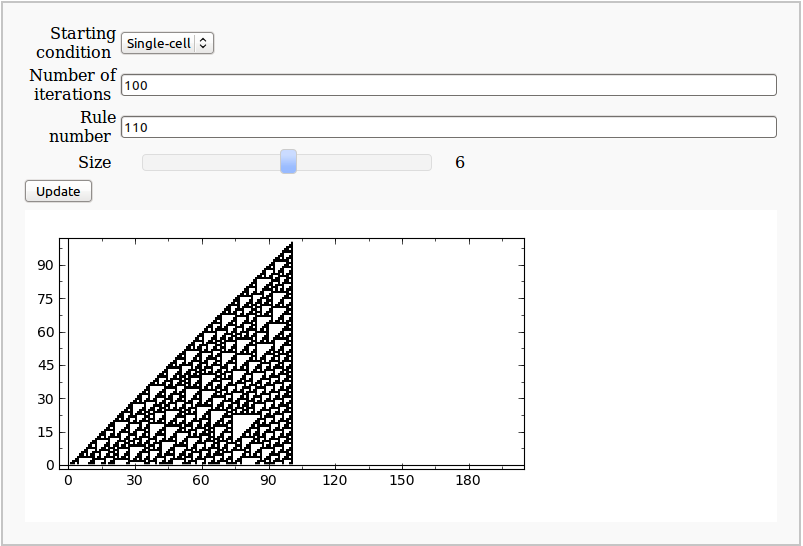
Cellular Automata
by Pablo Angulo, Eviatar Bach
xxxxxxxxxx%pythonfrom numpy import zerosfrom random import randintdef cellular(rule, N, initial='Single-cell'): '''Yields a matrix showing the evolution of a Wolfram's cellular automaton rule: determines how a cell's value is updated, depending on its neighbors N: number of iterations initial: starting condition; can be either single-cell or a random binary row ''' M=zeros( (N,2*N+2), dtype=int) if initial=='Single-cell': M[0,N]=1 else: M[0]=[randint(0,1) for a in range(0,2*N+2)] for j in range(1,N): for k in range(0,2*N): l = 4*M[j-1,k-1] + 2*M[j-1,k] + M[j-1,k+1] M[j,k]=rule[ l ] return M[:,:-1] def num2rule(number): if not 0 <= number <= 255: raise Exception('Invalid rule number') binary_digits = number.digits(base=2) return binary_digits + [0]*(8-len(binary_digits))Put in separate cell:
xxxxxxxxxxdef _( initial=selector(['Single-cell', 'Random'], label='Starting condition'), N=input_box(label='Number of iterations',default=100), rule_number=input_box(label='Rule number',default=110), size = slider(1, 11, label= 'Size', step_size=1, default=6 ), auto_update=False): rule = num2rule(rule_number) M = cellular(rule, N, initial) plot_M = matrix_plot(M, cmap='binary') plot_M.show( figsize=[size,size])