|
Size: 14340
Comment:
|
Size: 12838
Comment: Python 3 for Venn Diagram
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 123: | Line 123: |
| html("$X \cap Y$ = %s"%f(XY)) html("$X \cap Z$ = %s"%f(XZ)) html("$Y \cap Z$ = %s"%f(YZ)) html("$X \cap Y \cap Z$ = %s"%f(XYZ)) |
html("$X \\cap Y$ = {}".format(f(XY))) html("$X \\cap Z$ = {}".format(f(XZ))) html("$Y \\cap Z$ = {}".format(f(YZ))) html("$X \\cap Y \\cap Z$ = {}".format(f(XYZ))) |
| Line 198: | Line 198: |
| print globals()[system].eval(code) | print(globals()[system].eval(code)) |
| Line 207: | Line 207: |
| def minkdemo(list1,list2): | def minkdemo(list1, list2): |
| Line 209: | Line 209: |
| Returns the Minkowski sum of two lists. | Return the Minkowski sum of two lists. |
| Line 214: | Line 214: |
| temp = [stuff1[i] + stuff2[i] for i in range(len(stuff1))] output.append(temp) |
output.append([a + b for a, b in zip(stuff1, stuff2)]) |
| Line 217: | Line 216: |
| @interact def minksumvis(x1tri = slider(-1,1,1/10,0, label = 'Triangle point x coord.'), yb = slider(1,4,1/10,2, label = 'Blue point y coord.')): t_list = [[1,0],[x1tri,1],[0,0]] |
@interact def minksumvis(x1tri=slider(-1,1,1/10,0, label='Triangle point x coord.'), yb=slider(1,4,1/10,2, label='Blue point y coord.')): t_list = [[1,0], [x1tri,1], [0,0]] |
| Line 230: | Line 230: |
| for an_edge in p12poly.vertex_adjacencies(): edge_lines += line([verts[an_edge[0]], verts[an_edge[1][0]]]) edge_lines += line([verts[an_edge[0]], verts[an_edge[1][1]]]) |
for v0, v1 in p12poly.graph().edges(False): edge_lines += line([v0, v1]) |
| Line 302: | Line 301: |
| Line 312: | Line 311: |
| Line 317: | Line 316: |
| Line 325: | Line 324: |
| Line 333: | Line 332: |
| Line 336: | Line 335: |
| Line 338: | Line 337: |
| C=T-XX-YY-ZZ-ZX-ZY-YX-XYZ | C = T-XX-YY-ZZ-ZX-ZY-YX-XYZ |
| Line 342: | Line 341: |
| if XYZ>XY or XYZ>XZ or XYZ>YZ or XY>X or XY>Y or XZ>X or XZ>Z or YZ>Y or YZ>Z or C<0: print 'This situation is impossible!' if XYZ > XY: print 'The number of people who run, bike, and swim cannot be greater than the number of people who run and bike! (Why?)' if XYZ > XZ: print 'The number of people who run, bike, and swim cannot be greater than the number of people who run and swim! (Why?)' if XYZ > YZ: print 'The number of people who run, bike, and swim cannot be greater than the number of people who bike and swim! (Why?)' if XY > X: print 'The number of people who run and bike cannot be greater than the number of people who run! (Why?)' if XY > Y: print 'The number of people who run and bike cannot be greater than the number of people who bike! (Why?)' if XZ > X: print 'The number of people who run and swim cannot be greater than the number of people who run! (Why?)' if XZ > Z: print 'The number of people who run and swim cannot be greater than the number of people who swim! (Why?)' if YZ > Y: print 'The number of people who bike and swim cannot be greater than the number of people who bike! (Why?)' if YZ > Z: print 'The number of people who bike and swim cannot be greater than the number of people who swim! (Why?)' if C<0: print 'You have indicated too many people! The number of people exceeds the number of people surveyed. (Why?)' |
if XYZ>XY or XYZ>XZ or XYZ>YZ or XY>X or XY>Y or XZ>X or XZ>Z or YZ>Y or YZ>Z or C<0 or XYZ<0 or XZ<0 or YZ<0 or XY<0 or X<0 or Y<0 or Z<0: print('This situation is impossible! (Why?)') |
Sage Interactions - Miscellaneous
goto interact main page
Contents
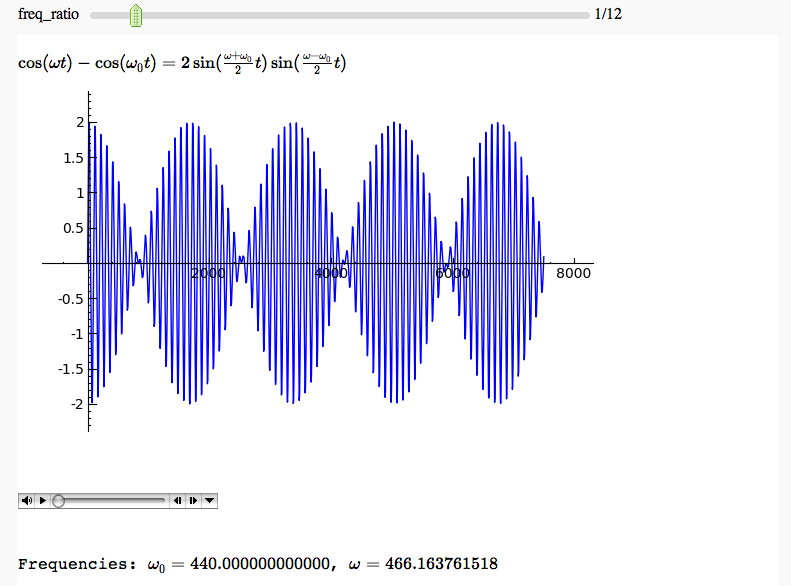
Hearing a trigonometric identity
by Marshall Hampton. When the two frequencies are well separated, we hear the right hand side of the identity. When they start getting close, we hear the higher-pitched factor in the left-hand side modulated by the lower-pitched envelope.
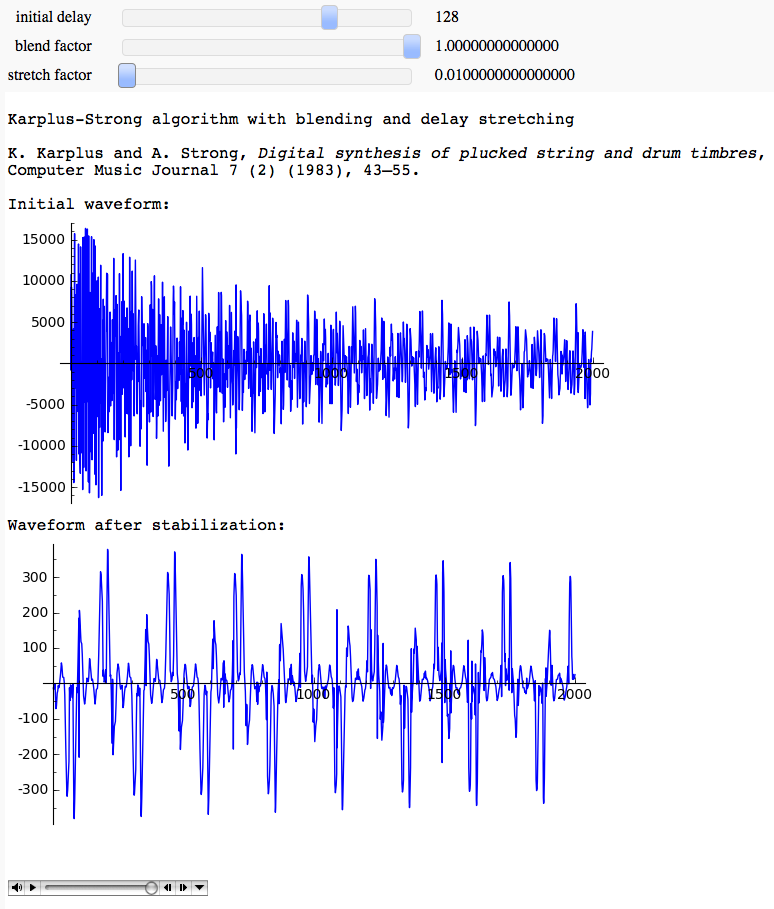
Karplus-Strong algorithm for plucked and percussive sound generation
by Marshall Hampton
An Interactive Venn Diagram
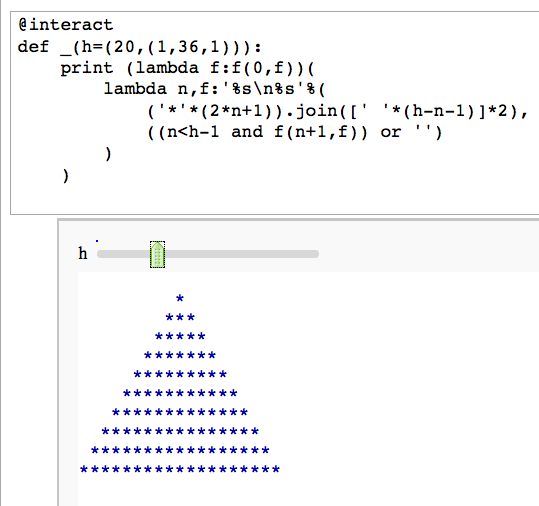
Unreadable code
by Igor Tolkov
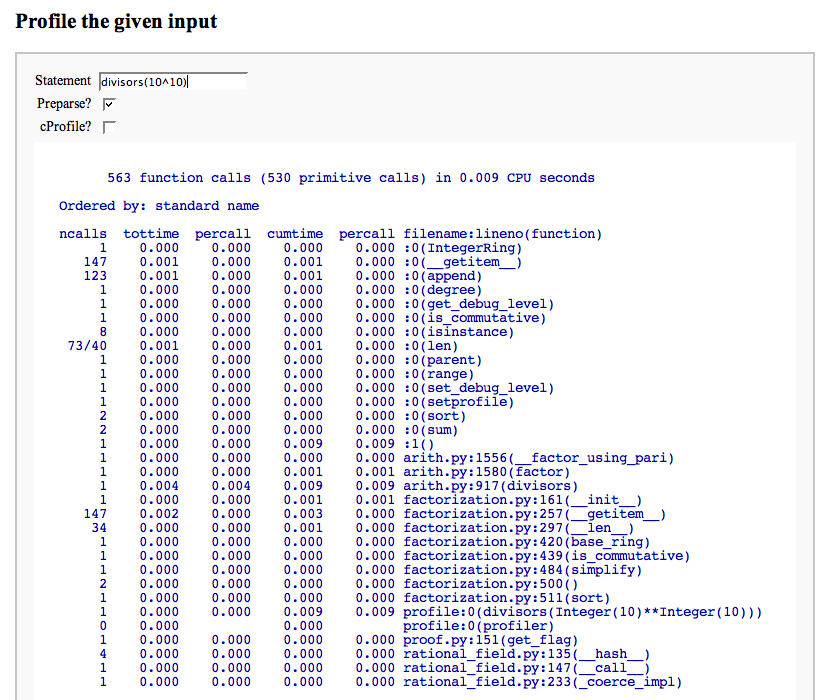
Profile a snippet of code
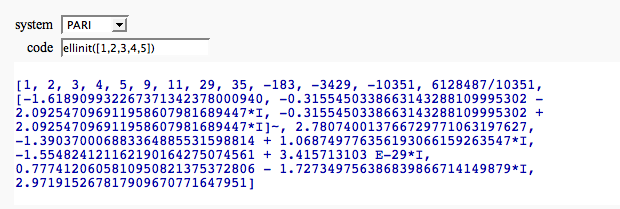
Evaluate a bit of code in a given system
by William Stein (there is no way yet to make the text box big):
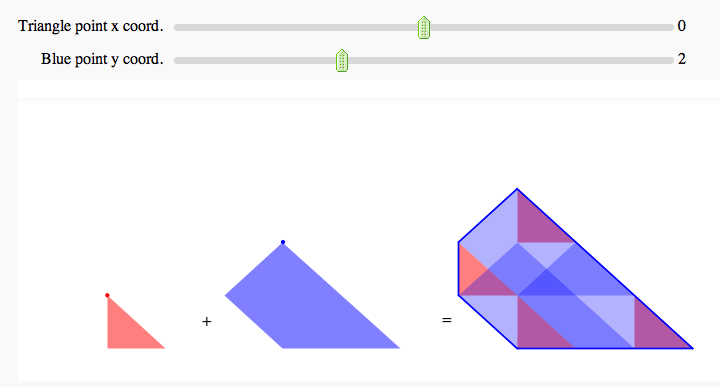
Minkowski Sum
by Marshall Hampton
Cellular Automata
by Pablo Angulo, Eviatar Bach
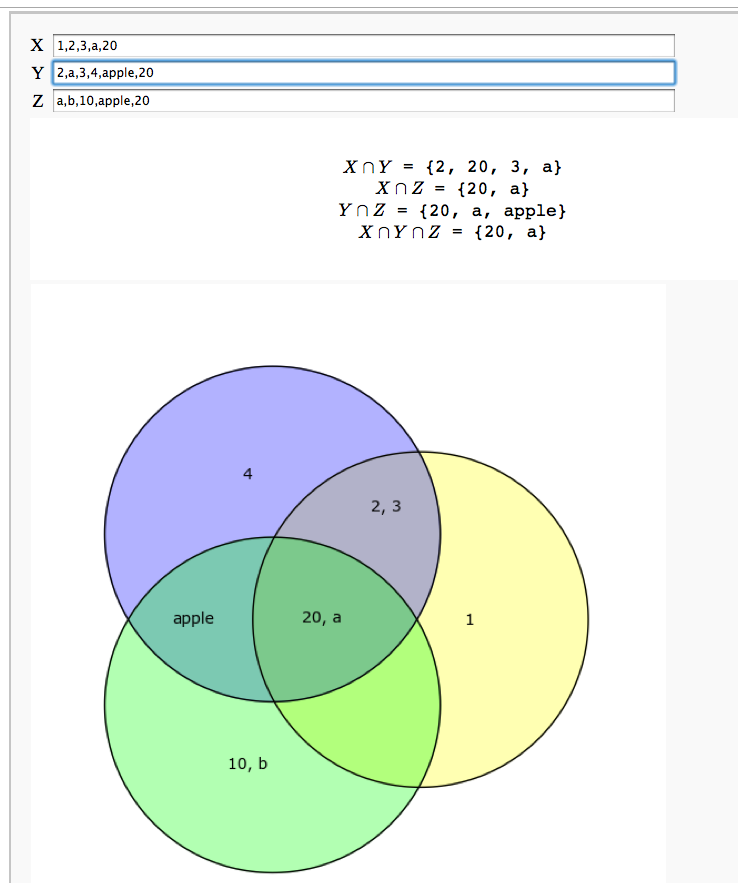
Another Interactive Venn Diagram
by Jane Long (adapted from http://wiki.sagemath.org/interact/misc)
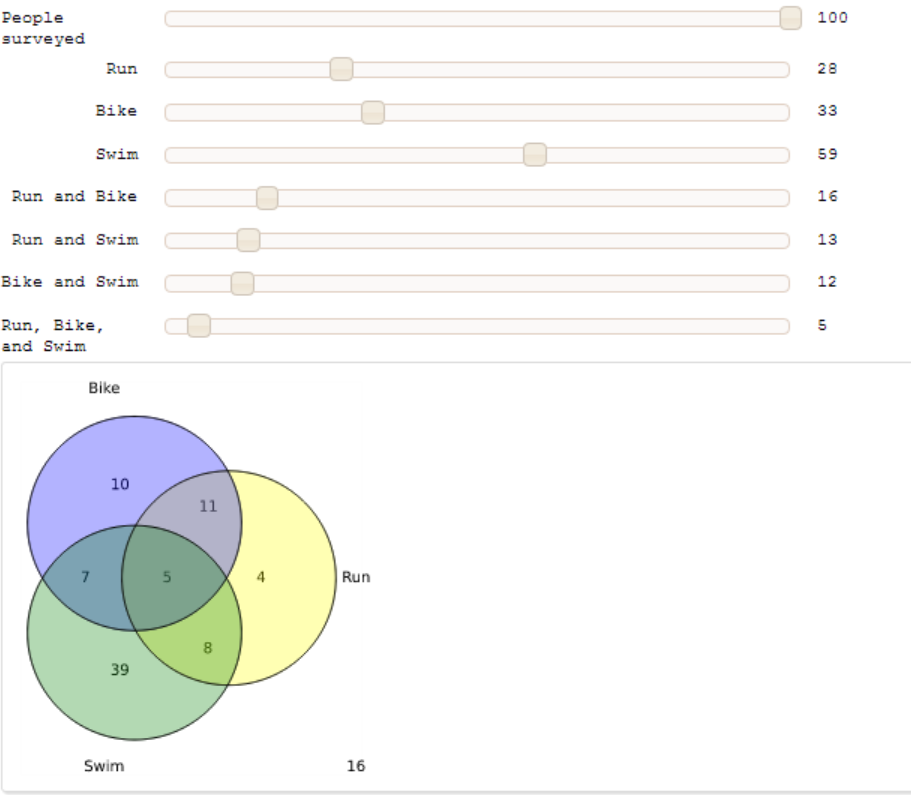
This interact models a problem in which a certain number of people are surveyed to see if they participate in three different activities (running, biking, and swimming). Users can indicate the numbers of people in each category, from 0 to 100. Returns a graphic of a labeled Venn diagram with the number of people in each region. Returns an explanatory error message if user input is inconsistent.