|
Size: 10234
Comment:
|
Size: 12839
Comment: Python 3 for Unreadable code
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 123: | Line 123: |
| html("$X \cap Y$ = %s"%f(XY)) html("$X \cap Z$ = %s"%f(XZ)) html("$Y \cap Z$ = %s"%f(YZ)) html("$X \cap Y \cap Z$ = %s"%f(XYZ)) |
html("$X \\cap Y$ = {}".format(f(XY))) html("$X \\cap Z$ = {}".format(f(XZ))) html("$Y \\cap Z$ = {}".format(f(YZ))) html("$X \\cap Y \\cap Z$ = {}".format(f(XYZ))) |
| Line 166: | Line 166: |
| print (lambda f:f(0,f))( | print9(lambda f:f(0,f))( |
| Line 171: | Line 171: |
| ) | )) |
| Line 198: | Line 198: |
| print globals()[system].eval(code) | print(globals()[system].eval(code)) |
| Line 207: | Line 207: |
| def minkdemo(list1,list2): | def minkdemo(list1, list2): |
| Line 209: | Line 209: |
| Returns the Minkowski sum of two lists. | Return the Minkowski sum of two lists. |
| Line 214: | Line 214: |
| temp = [stuff1[i] + stuff2[i] for i in range(len(stuff1))] output.append(temp) |
output.append([a + b for a, b in zip(stuff1, stuff2)]) |
| Line 217: | Line 216: |
| @interact def minksumvis(x1tri = slider(-1,1,1/10,0, label = 'Triangle point x coord.'), yb = slider(1,4,1/10,2, label = 'Blue point y coord.')): t_list = [[1,0],[x1tri,1],[0,0]] |
@interact def minksumvis(x1tri=slider(-1,1,1/10,0, label='Triangle point x coord.'), yb=slider(1,4,1/10,2, label='Blue point y coord.')): t_list = [[1,0], [x1tri,1], [0,0]] |
| Line 230: | Line 230: |
| for an_edge in p12poly.vertex_adjacencies(): edge_lines += line([verts[an_edge[0]], verts[an_edge[1][0]]]) edge_lines += line([verts[an_edge[0]], verts[an_edge[1][1]]]) |
for v0, v1 in p12poly.graph().edges(False): edge_lines += line([v0, v1]) |
| Line 293: | Line 292: |
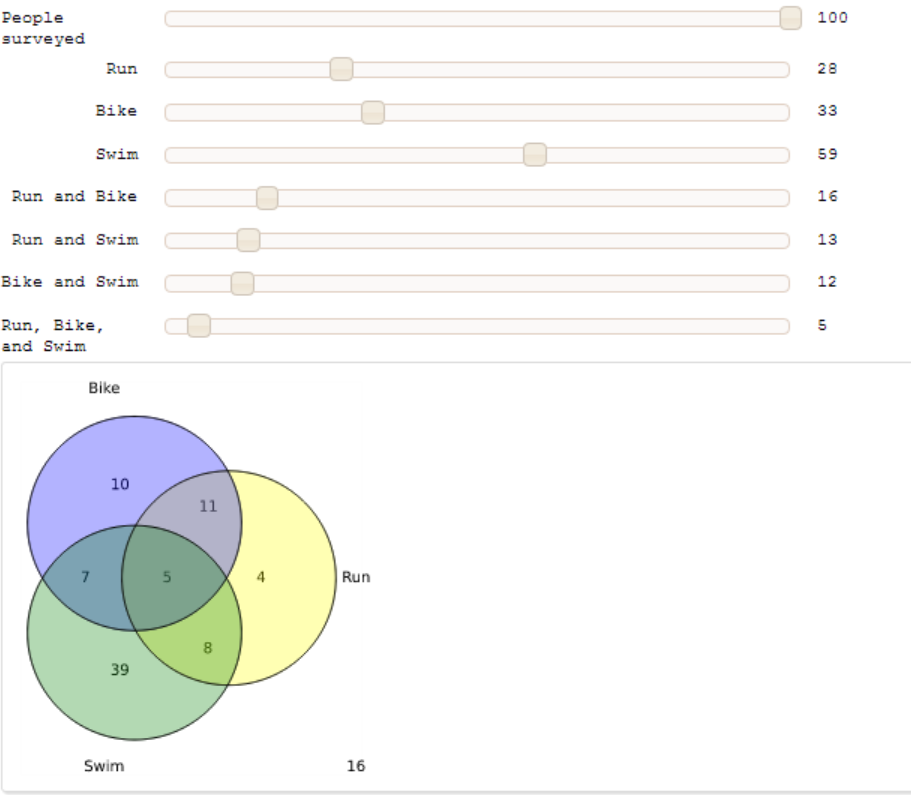
== Another Interactive Venn Diagram == by Jane Long (adapted from http://wiki.sagemath.org/interact/misc) This interact models a problem in which a certain number of people are surveyed to see if they participate in three different activities (running, biking, and swimming). Users can indicate the numbers of people in each category, from 0 to 100. Returns a graphic of a labeled Venn diagram with the number of people in each region. Returns an explanatory error message if user input is inconsistent. {{{#!sagecell @interact def _(T=slider([0..100],default=100,label='People surveyed'),X=slider([0..100],default=28,label='Run'), Y=slider([0..100],default=33,label='Bike'), Z=slider([0..100],default=59,label='Swim'),XY=slider([0..100],default=16,label='Run and Bike'),XZ=slider([0..100],default=13,label='Run and Swim'),YZ=slider([0..100],default=12,label='Bike and Swim'),XYZ=slider([0..100],default=7,label='Run, Bike, and Swim')): centers = [(cos(n*2*pi/3), sin(n*2*pi/3)) for n in [0,1,2]] scale = 1.7 clr = ['yellow', 'blue', 'green'] G = Graphics() for i in range(3): G += circle(centers[i], scale, rgbcolor=clr[i], fill=True, alpha=0.3) for i in range(3): G += circle(centers[i], scale, rgbcolor='black') # Label sets G += text('Run',(3,0),rgbcolor='black') G += text('Bike',(-1,3),rgbcolor='black') G += text('Swim',(-1,-3),rgbcolor='black') # Plot pairs of intersections ZX=XZ-XYZ G += text(ZX, (1.3*cos(2*2*pi/3 + pi/3), 1.3*sin(2*2*pi/3 + pi/3)), rgbcolor='black') YX=XY-XYZ G += text(YX, (1.3*cos(0*2*pi/3 + pi/3), 1.3*sin(0*2*pi/3 + pi/3)), rgbcolor='black') ZY=YZ-XYZ G += text(ZY, (1.3*cos(1*2*pi/3 + pi/3), 1.3*sin(1*2*pi/3 + pi/3)), rgbcolor='black') # Plot what is in one but neither other XX=X-ZX-YX-XYZ G += text(XX, (1.5*centers[0][0],1.7*centers[0][1]), rgbcolor='black') YY=Y-ZY-YX-XYZ G += text(YY, (1.5*centers[1][0],1.7*centers[1][1]), rgbcolor='black') ZZ=Z-ZY-ZX-XYZ G += text(ZZ, (1.5*centers[2][0],1.7*centers[2][1]), rgbcolor='black') # Plot intersection of all three G += text(XYZ, (0,0), rgbcolor='black') # Indicate number not in X, in Y, or in Z C = T-XX-YY-ZZ-ZX-ZY-YX-XYZ G += text(C,(3,-3),rgbcolor='black') # Check reasonableness before displaying result if XYZ>XY or XYZ>XZ or XYZ>YZ or XY>X or XY>Y or XZ>X or XZ>Z or YZ>Y or YZ>Z or C<0 or XYZ<0 or XZ<0 or YZ<0 or XY<0 or X<0 or Y<0 or Z<0: print('This situation is impossible! (Why?)') else: G.show(aspect_ratio=1, axes=False) }}} {{attachment:vennjhl.png}} |
Sage Interactions - Miscellaneous
goto interact main page
Contents
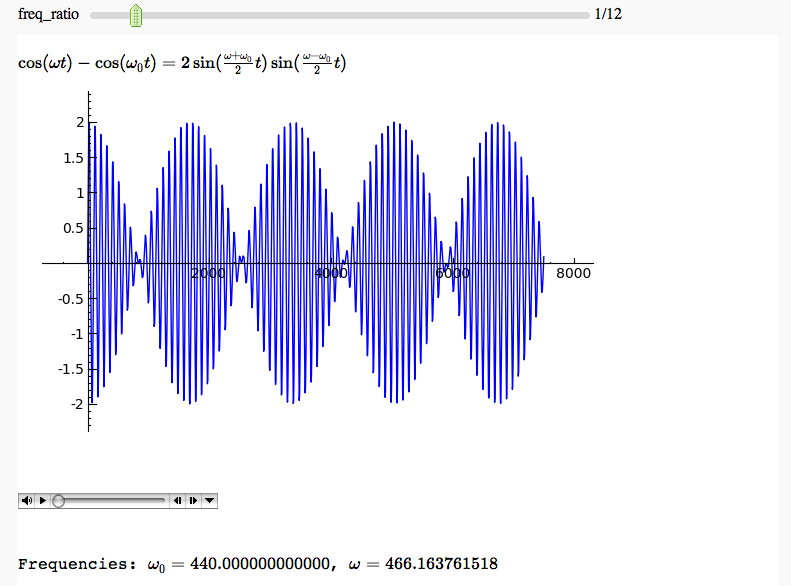
Hearing a trigonometric identity
by Marshall Hampton. When the two frequencies are well separated, we hear the right hand side of the identity. When they start getting close, we hear the higher-pitched factor in the left-hand side modulated by the lower-pitched envelope.
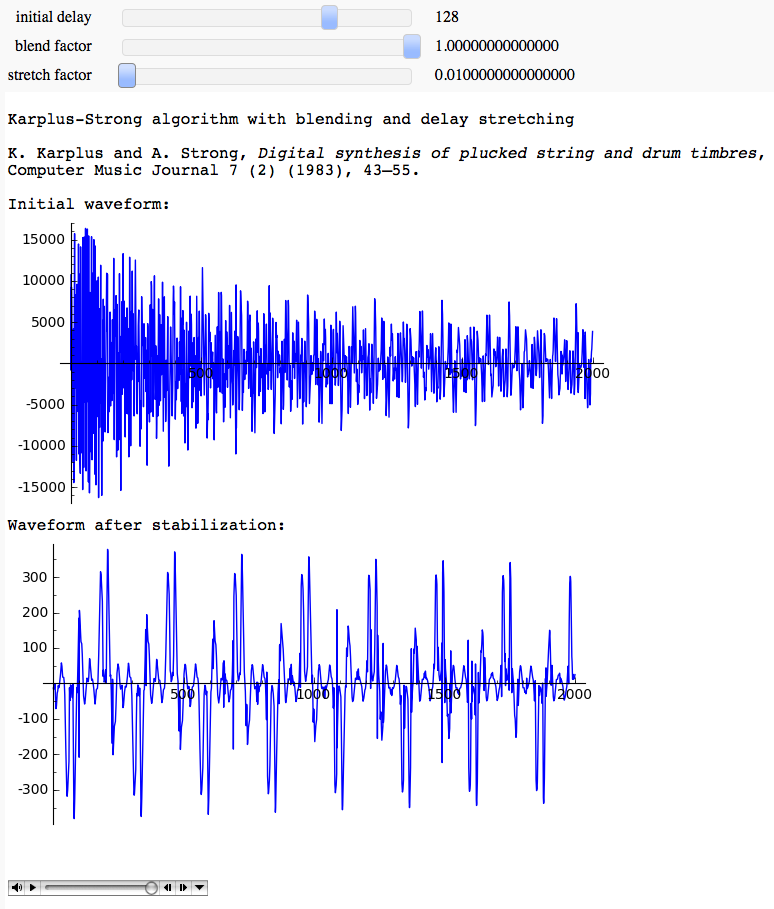
Karplus-Strong algorithm for plucked and percussive sound generation
by Marshall Hampton
An Interactive Venn Diagram
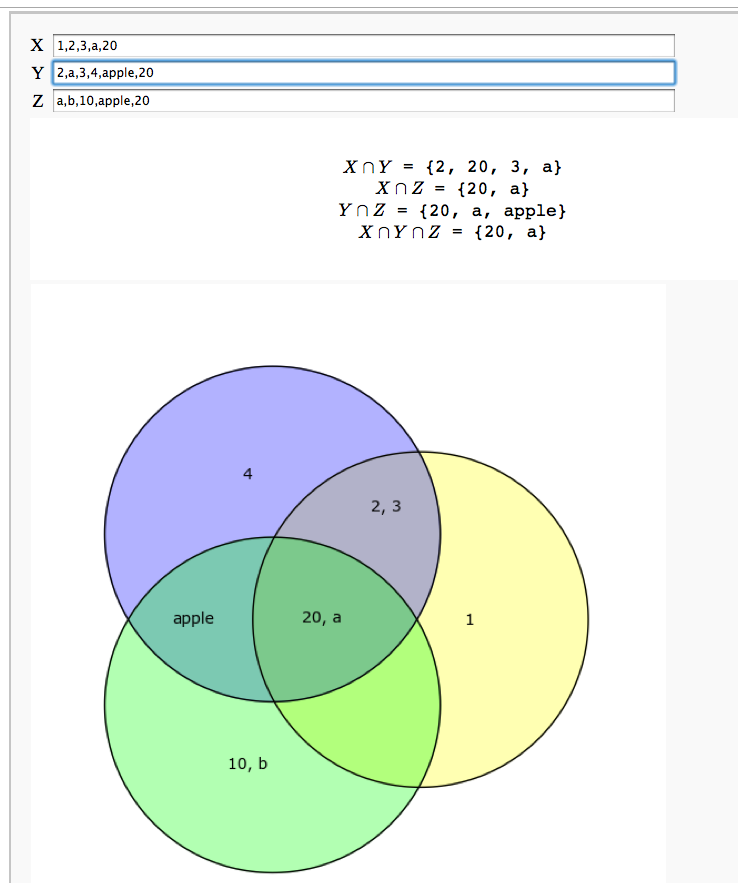
Unreadable code
by Igor Tolkov
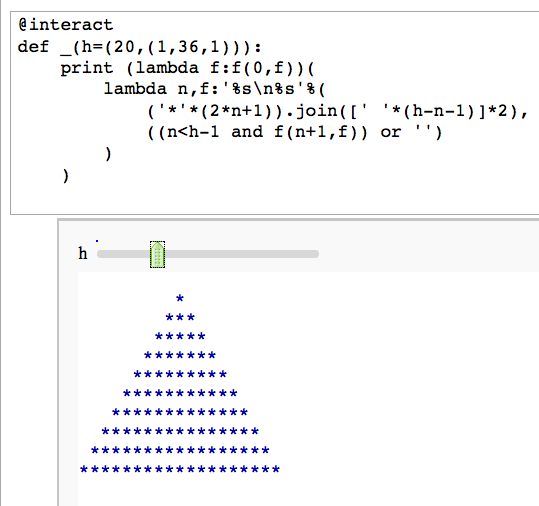
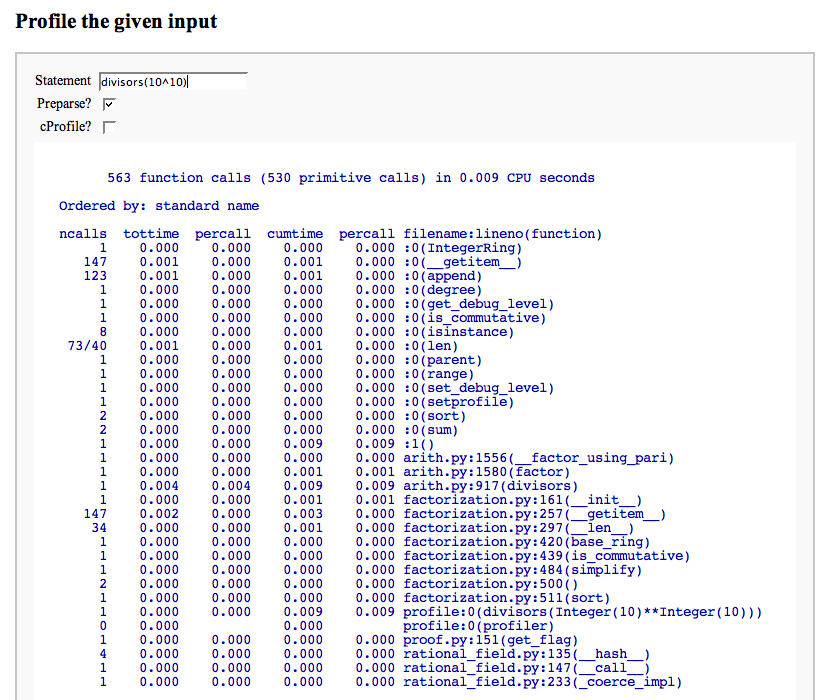
Profile a snippet of code
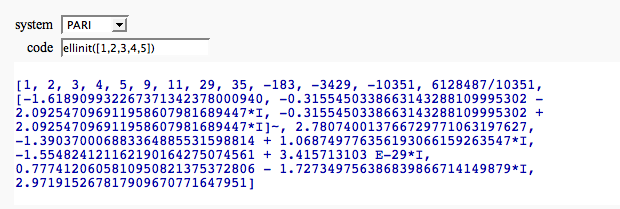
Evaluate a bit of code in a given system
by William Stein (there is no way yet to make the text box big):
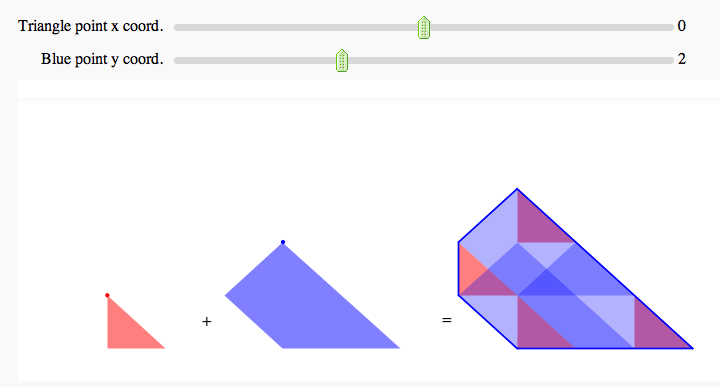
Minkowski Sum
by Marshall Hampton
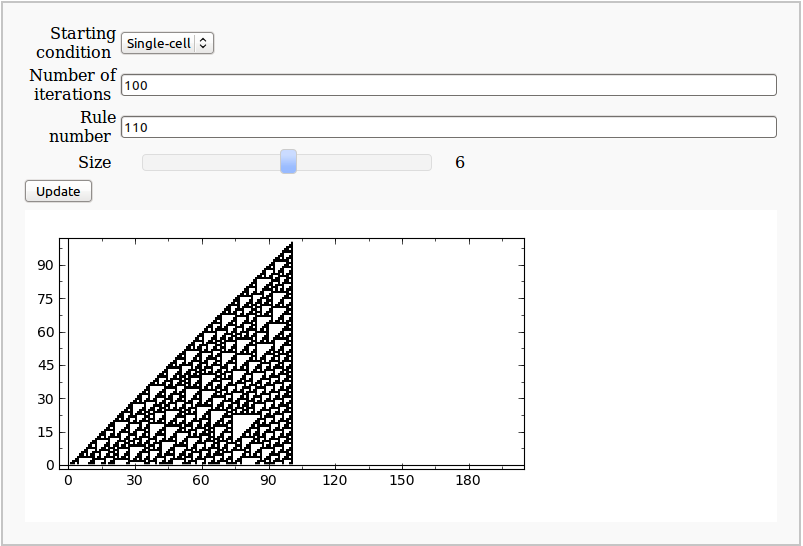
Cellular Automata
by Pablo Angulo, Eviatar Bach
Another Interactive Venn Diagram
by Jane Long (adapted from http://wiki.sagemath.org/interact/misc)
This interact models a problem in which a certain number of people are surveyed to see if they participate in three different activities (running, biking, and swimming). Users can indicate the numbers of people in each category, from 0 to 100. Returns a graphic of a labeled Venn diagram with the number of people in each region. Returns an explanatory error message if user input is inconsistent.