|
Size: 7011
Comment:
|
← Revision 35 as of 2020-11-27 12:10:23 ⇥
Size: 19683
Comment: credit to Hristo Inouzhe by Pablo Angulo on the last two interacts
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| goto [:interact:interact main page] [[TableOfContents]] |
goto [[interact|interact main page]] <<TableOfContents>> |
| Line 7: | Line 7: |
| by Marshall Hampton (tested by William Stein, who thinks this is really nice!) {{{ |
by Marshall Hampton {{{#!sagecell |
| Line 19: | Line 19: |
| v = [a_list[i].copy() for i in indices] | v = [a_list[i][:] for i in indices] |
| Line 24: | Line 24: |
| r[i][i] = (v[i]*v[i])^(1/2) | r[i][i] = (v[i]*v[i])**(1/2) |
| Line 38: | Line 38: |
| v = [a_list[i].copy() for i in indices] | v = [a_list[i][:] for i in indices] |
| Line 47: | Line 47: |
| html('<h2>Numerical instability of the classical Gram-Schmidt algorithm</h2>') | pretty_print(html('<h2>Numerical instability of the classical Gram-Schmidt algorithm</h2>')) |
| Line 52: | Line 52: |
| html('precision in bits: ' + str(precision) + '<br>') | pretty_print(html('precision in bits: ' + str(precision) + '<br>')) |
| Line 57: | Line 57: |
| html('Classical Gram-Schmidt:') | pretty_print(html('Classical Gram-Schmidt:')) |
| Line 59: | Line 59: |
| html('Stable Gram-Schmidt:') | pretty_print(html('Stable Gram-Schmidt:')) |
| Line 62: | Line 62: |
| attachment:GramSchmidt.png | {{attachment:GramSchmidt.png}} == Equality of det(A) and det(A.tranpose()) == by Marshall Hampton {{{#!sagecell srg = srange(-4,4,1/10,include_endpoint=True) @interact def dualv(a1=slider(srg,default=1),a2=slider(srg,default=2), a3=slider(srg,default=-1),a4=slider(srg,default=3)): A1 = arrow2d([0,0],[a1,a2],rgbcolor='black') A2 = arrow2d([0,0],[a3,a4],rgbcolor='black') A3 = arrow2d([0,0],[a1,a3],rgbcolor='black') A4 = arrow2d([0,0],[a2,a4],rgbcolor='black') p1 = polygon([[0,0],[a1,a2],[a1+a3,a2+a4],[a3,a4],[0,0]], alpha=.5) p2 = polygon([[0,0],[a1,a3],[a1+a2,a3+a4],[a2,a4],[0,0]],rgbcolor='red', alpha=.5) A = matrix([[a1,a2],[a3,a4]]) pretty_print(html('<h3>The determinant of a matrix is equal to the determinant of the transpose</h3>')) pretty_print(html("$\det(%s) = \det(%s)=%s$"%(latex(A),latex(A.transpose()),latex(RR(A.determinant()))))) show(A1+A2+A3+A4+p1+p2) }}} {{attachment:Det_transpose_new.png}} |
| Line 69: | Line 88: |
| {{{ @interact def linear_transformation(theta=slider(0, 2*pi, .1), r=slider(0.1, 2, .1, default=1)): A=matrix([[1,-1],[-1,1/2]]) |
{{{#!sagecell @interact def linear_transformation(A=matrix([[1,-1],[-1,1/2]]),theta=slider(0, 2*pi, .1), r=slider(0.1, 2, .1, default=1)): |
| Line 75: | Line 93: |
| circles = sum([circle((0,0), radius=i, rgbcolor=(0,0,0)) for i in [1..2]]) print jsmath("v = %s,\; %s v=%s"%(v.n(4),latex(A),w.n(4))) show(v.plot(rgbcolor=(1,0,0))+w.plot(rgbcolor=(0,0,1))+circles,aspect_ratio=1) }}} attachment:Linear-Transformations.png |
circles = sum([circle((0,0), radius=i, color='black') for i in [1..2]]) pretty_print(html("$%s %s=%s$"%tuple(map(latex, [A, v.column().n(4), w.column().n(4)])))) show(v.plot(color='red')+w.plot(color='blue')+circles,aspect_ratio=1) }}} {{attachment:Linear-Transformations.png}} |
| Line 82: | Line 100: |
| by Marshall Hampton {{{ |
by Marshall Hampton. This animated version requires convert (imagemagick) to be installed, but it can easily be modified to a static version. The animation illustrates the idea behind the stronger version of Gerschgorin's theorem, which says that if the disks around the eigenvalues are disjoint then there is one eigenvalue per disk. The proof is by continuity of the eigenvalues under a homotopy to a diagonal matrix. {{{#!sagecell |
| Line 85: | Line 104: |
| html('<h2>The Gerschgorin circle theorem</h2>') @interact def Gerschgorin(A = input_grid(4, 4, default=[[10,1,1,0],[-1,9,0,.1],[1,0,2,.3],[-.5 ,0,-.3,1]], label='A = ', to_value=lambda x:x, width=4)): print jsmath('A = ' + latex(matrix(RealField(10),A))) eigs = [CDF(x) for x in linalg.eigvals(matrix(A).numpy())] eigpoints = points([(real(q),imag(q)) for q in eigs],pointsize = 10, rgbcolor = (0,0,0)) centers = [(real(q),imag(q)) for q in [A[i][i] for i in range(4)]] radii_row = [sum([abs(A[i][j]) for j in range(i)+range(i+1,4)]) for i in range(4)] radii_col = [sum([abs(A[j][i]) for j in range(i)+range(i+1,4)]) for i in range(4)] x_min = min([centers[i][0]-radii_row[i] for i in range(4)]+[centers[i][0]-radii_col[i] for i in range(4)]) x_max = max([centers[i][0]+radii_row[i] for i in range(4)]+[centers[i][0]+radii_col[i] for i in range(4)]) y_min = min([centers[i][1]-radii_row[i] for i in range(4)]+[centers[i][1]-radii_col[i] for i in range(4)]) y_max = max([centers[i][1]+radii_row[i] for i in range(4)]+[centers[i][1]+radii_col[i] for i in range(4)]) scale = max([(x_max-x_min),(y_max-y_min)]) scale = 7/scale row_circles = sum([circle(centers[i],radii_row[i],fill=True, alpha = .3) for i in range(4)]) col_circles = sum([circle(centers[i],radii_col[i],fill=True, rgbcolor = (1,1,0), alpha = .3) for i in range(4)]) show(eigpoints+row_circles+col_circles, figsize = [(x_max-x_min)*scale,(y_max-y_min)*scale], xmin = x_min, xmax=x_max, ymin = y_min, ymax = y_max) }}} attachment:gerschgorin.png |
pretty_print(html('<h2>The Gerschgorin circle theorem</h2>')) @interact def Gerschgorin(Ain = input_box(default='[[10,1,1/10,0],[-1,9,0,1],[1,0,2,3/10],[-.5,0,-.3,1]]', type = str, label = 'A = '), an_size = slider(1,100,1,1.0)): A = sage_eval(Ain) size = len(A) pretty_print(html('$A = ' + latex(matrix(RealField(10),A))+'$')) A = matrix(RealField(10),A) B = [[0 for i in range(size)] for j in range(size)] for i in range(size): B[i][i] = A[i][i] B = matrix(B) frames = [] centers = [(real(q),imag(q)) for q in [A[i][i] for i in range(size)]] radii_row = [sum([abs(A[i][j]) for j in range(i)+range(i+1,size)]) for i in range(size)] radii_col = [sum([abs(A[j][i]) for j in range(i)+range(i+1,size)]) for i in range(size)] x_min = min([centers[i][0]-radii_row[i] for i in range(size)]+[centers[i][0]-radii_col[i] for i in range(size)]) x_max = max([centers[i][0]+radii_row[i] for i in range(size)]+[centers[i][0]+radii_col[i] for i in range(size)]) y_min = min([centers[i][1]-radii_row[i] for i in range(size)]+[centers[i][1]-radii_col[i] for i in range(size)]) y_max = max([centers[i][1]+radii_row[i] for i in range(size)]+[centers[i][1]+radii_col[i] for i in range(size)]) if an_size > 1: t_range= srange(0,1+1/an_size,1/an_size) else: t_range = [1] for t in t_range: C = t*A + (1-t)*B eigs = [CDF(x) for x in linalg.eigvals(C.numpy())] eigpoints = points([(real(q),imag(q)) for q in eigs],pointsize = 10, rgbcolor = (0,0,0)) centers = [(real(q),imag(q)) for q in [A[i][i] for i in range(size)]] radii_row = [sum([abs(C[i][j]) for j in range(i)+range(i+1,size)]) for i in range(size)] radii_col = [sum([abs(C[j][i]) for j in range(i)+range(i+1,size)]) for i in range(size)] scale = max([(x_max-x_min),(y_max-y_min)]) scale = 7/scale row_circles = sum([circle(centers[i],radii_row[i],fill=True, alpha = .3) for i in range(size)]) col_circles = sum([circle(centers[i],radii_col[i],fill=True, rgbcolor = (1,0,0), alpha = .3) for i in range(size)]) ft = eigpoints+row_circles+col_circles frames.append(ft) show(animate(frames,figsize = [(x_max-x_min)*scale,(y_max-y_min)*scale], xmin = x_min, xmax=x_max, ymin = y_min, ymax = y_max)) }}} {{attachment:Gerschanimate.png}} {{attachment:Gersch.gif}} |
| Line 109: | Line 150: |
| {{{ | {{{#!sagecell |
| Line 116: | Line 157: |
| def svd_vis(a11=slider(-1,1,.05,1),a12=slider(-1,1,.05,1),a21=slider(-1,1,.05,0),a22=slider(-1,1,.05,1),ofs= selector(['Off','On'],label='offset image from domain')): | def svd_vis(a11=slider(-1,1,.05,1),a12=slider(-1,1,.05,1),a21=slider(-1,1,.05,0),a22=slider(-1,1,.05,1),ofs= ('offset image from domain',False)): |
| Line 120: | Line 161: |
| if ofs == 'On': | if ofs: |
| Line 132: | Line 173: |
| html('<h3>Singular value decomposition: image of the unit circle and the singular vectors</h3>') print jsmath("A = %s = %s %s %s"%(latex(my_mat), latex(matrix(rf_low,u.tolist())), latex(matrix(rf_low,2,2,[s[0],0,0,s[1]])), latex(matrix(rf_low,vh.tolist())))) image_ell = parametric_plot(rotell(s,u,t, offset),0,2*pi) |
pretty_print(html('<h3>Singular value decomposition: image of the unit circle and the singular vectors</h3>')) pretty_print(html("$A = %s = %s %s %s$"%(latex(my_mat), latex(matrix(rf_low,u.tolist())), latex(matrix(rf_low,2,2,[s[0],0,0,s[1]])), latex(matrix(rf_low,vh.tolist()))))) image_ell = parametric_plot(rotell(s,u,t, offset),(0,2*pi)) |
| Line 137: | Line 178: |
| show(graph_stuff,frame = False,axes=False,figsize=[fsize,fsize]) }}} attachment:svd1.png |
show(graph_stuff,frame = False,axes=False,figsize=[fsize,fsize])}}} {{attachment:svd1.png}} |
| Line 143: | Line 183: |
| {{{ | {{{#!sagecell |
| Line 147: | Line 187: |
| var('x') | |
| Line 150: | Line 189: |
| html("<h3>Function plot and its discrete Fourier transform</h3>") show(plot(f, pbegin, pend, plot_points = 512), figsize = [4,3]) f_vals = [f(ind) for ind in srange(pbegin, pend,(pend-pbegin)/512.0)] |
pretty_print(html("<h3>Function plot and its discrete Fourier transform</h3>")) show(plot(f, (x,pbegin, pend), plot_points = 512), figsize = [4,3]) f_vals = [f(x=ind) for ind in srange(pbegin, pend,(pend-pbegin)/512.0)] |
| Line 154: | Line 193: |
| show(list_plot([abs(x) for x in my_fft], plotjoined=True), figsize = [4,3]) }}} attachment:dfft1.png |
show(list_plot([abs(i) for i in my_fft], plotjoined=True), figsize = [4,3]) }}} {{attachment:dfft1.png}} == The Gauss-Jordan method for inverting a matrix == by Hristo Inouzhe {{{#!sagecell #Choose the size D of the square matrix: D = 3 example = [[1 if k==j else 0 for k in range(D)] for j in range(D)] example[0][-1] = 2 example[-1][0] = 3 @interact def _(M=input_grid(D,D, default = example, label='Matrix to invert', to_value=matrix), tt = text_control('Enter the bits of precision used' ' (only if you entered floating point numbers)'), precision = slider(5,100,5,20), auto_update=False): if det(M)==0: print 'Failure: Matrix is not invertible' return if M.base_ring() == RR: M = M.apply_map(RealField(precision)) N=M M=M.augment(identity_matrix(D)) print 'We construct the augmented matrix' show(M) for m in range(0,D-1): if M[m,m] == 0: lista = [(abs(M[j,m]),j) for j in range(m+1,D)] maxi, c = max(lista) M[c,:],M[m,:]=M[m,:],M[c,:] print 'We permute rows %d and %d'%(m+1,c+1) show(M) for n in range(m+1,D): a=M[m,m] if M[n,m]!=0: print "We add %s times row %d to row %d"%(-M[n,m]/a, m+1, n+1) M=M.with_added_multiple_of_row(n,m,-M[n,m]/a) show(M) for m in range(D-1,-1,-1): for n in range(m-1,-1,-1): a=M[m,m] if M[n,m]!=0: print "We add %s times row %d to the row %d"%(-M[n,m]/a, m+1, n+1) M=M.with_added_multiple_of_row(n,m,-M[n,m]/a) show(M) for m in range(0,D): if M[m,m]!=1: print 'We divide row %d by %s'%(m+1,M[m,m]) M = M.with_row_set_to_multiple_of_row(m,m,1/M[m,m]) show(M) M=M.submatrix(0,D,D) print 'We keep the right submatrix, which contains the inverse' html('$$M^{-1}=%s$$'%latex(M)) print 'We check it actually is the inverse' html('$$M^{-1}*M=%s*%s=%s$$'%(latex(M),latex(N),latex(M*N))) }}} {{attachment:gauss-jordan.png}} ...(goes all the way to invert the matrix) == Solution of an homogeneous system of linear equations == by Pablo Angulo and Hristo Inouzhe Coefficients are introduced as a matrix in a single text box. The number of equations and unknowns are arbitrary. {{{#!sagecell from sage.misc.html import HtmlFragment def HSLE_as_latex(A, variables): nvars = A.ncols() pretty_print(HtmlFragment( r'$$\left\{\begin{array}{%s}'%('r'*(nvars+1))+ r'\\'.join('%s=&0'%( ' & '.join((r'%s%s\cdot %s'%('+' if c>0 else '',c,v) if c else '') for c,v in zip(row, variables)) if not row.is_zero() else '&'*(nvars-1)+'0' ) for row in A)+ r'\end{array}\right.$$')) @interact def SEL(A='[(0,1,-1,2),(-1,0,2,4), (0,-1,1,-2)]', auto_update=False ): M = A = matrix(eval(A)) neqs = M.nrows() nvars = M.ncols() var_names = ','.join('x%d'%j for j in [1..nvars]) variables = var(var_names) HSLE_as_latex(M, variables) pretty_print(HtmlFragment( 'SEL in matrix form')) show(M) pivot = {} ibound_variables = [] for m,row in enumerate(M): for k in range(m,nvars): lista = [(abs(M[j,k]),j) for j in range(m,neqs)] maxi, c = max(lista) if maxi > 0: ibound_variables.append(k) if M[m,k]==0: M[c,:],M[m,:]=M[m,:],M[c,:] pretty_print( HtmlFragment('We permute rows %d and %d'%(m+1,c+1))) show(M) pivot[m] = k break a=M[m,k] for n in range(m+1,neqs): if M[n,k]!=0: pretty_print( HtmlFragment("We add %s times row %d to row %d"%(-M[n,k]/a, m+1, n+1))) M=M.with_added_multiple_of_row(n,m,-M[n,k]/a) show(M) pretty_print( HtmlFragment('Equivalent system of equations')) HSLE_as_latex(M, variables) SEL_type = 'compatible' null_rows = None for k,row in enumerate(M): if row.is_zero(): pretty_print( HtmlFragment('We remove trivial 0=0 equations')) M = M[:k,:] HSLE_as_latex(M, variables) ifree_variables = [k for k in range(nvars) if k not in ibound_variables] bound_variables = [variables[k] for k in ibound_variables] free_variables = [variables[k] for k in ifree_variables] pretty_print( HtmlFragment('Free variables: %s'% free_variables)) pretty_print( HtmlFragment('Bound variables: %s'% bound_variables)) reduced_eqs = [ sum(c*v for c,v in zip(row, variables))==0 for row in M ] xvector = vector(variables) if len(bound_variables)==1: soldict = solve(reduced_eqs, bound_variables[0], solution_dict=True)[0] else: soldict = solve(reduced_eqs, bound_variables, solution_dict=True)[0] pretty_print( HtmlFragment('Solution in parametric form')) parametric_sol = matrix( xvector.apply_map(lambda s:s.subs(soldict)) ).transpose() show(parametric_sol) pretty_print( HtmlFragment('Generators')) pretty_print( HtmlFragment( r'$$\langle %s\rangle$$'%','.join(latex( parametric_sol.subs(dict((variables[k],1 if j==k else 0) for k in ifree_variables)) ) for j in ifree_variables) )) pretty_print( HtmlFragment('Dimension is %d'%len(free_variables))) }}} {{attachment:HSEL_1.png||width=600}} {{attachment:HSEL_2.png||width=600}} == Solution of a non homogeneous system of linear equations == by Pablo Angulo and Hristo Inouzhe Coefficients are introduced as a matrix in a single text box, and independent terms as a vector in a separate text box. The number of equations and unknowns are arbitrary. {{{#!sagecell from sage.misc.html import HtmlFragment def SLE_as_latex(A, b, variables): nvars = A.ncols() pretty_print(HtmlFragment( r'$$\left\{\begin{array}{%s}'%('r'*(nvars+1))+ r'\\'.join('%s=&%s'%( (' & '.join((r'%s%s\cdot %s'%('+' if c>0 else '',c,v) if c else '') for c,v in zip(row, variables)) if not row.is_zero() else '&'*(nvars-1)+'0',y) ) for row,y in zip(A,b))+ r'\end{array}\right.$$')) def extended_matrix_as_latex(M): A = M[:,:-1] b = M.column(-1) nvars = A.ncols() pretty_print(HtmlFragment( r'$$\left(\begin{array}{%s}'%('r'*nvars+ '|r')+ r'\\'.join('%s&%s'%( ' & '.join('%s'%c for c in row) ,y) for row,y in zip(A,b))+ r'\end{array}\right)$$')) @interact def SEL(A_text='[(0,0,-1,2),(-1,0,2,4), (0,0,1,-2)]', b_text='[2,1,-2]', auto_update=False ): A = matrix(eval(A_text)) b = vector(eval(b_text)) M = A.augment(b) neqs = len(b) nvars = A.ncols() var_names = ','.join('x%d'%j for j in [1..nvars]) variables = var(var_names) pretty_print(HtmlFragment('Variables: %s'% var_names)) for row,y in zip(A,b): pretty_print(HtmlFragment(sum(c*v for c,v in zip(row, variables))==y)) SLE_as_latex(A, b, variables) pretty_print(HtmlFragment( 'We construct the augmented matrix')) extended_matrix_as_latex(M) pivot = {} ibound_variables = [] for m,row in enumerate(A): for k in range(m,nvars): lista = [(abs(M[j,k]),j) for j in range(m,neqs)] maxi, c = max(lista) if maxi > 0: ibound_variables.append(k) if M[m,k]==0: M[c,:],M[m,:]=M[m,:],M[c,:] pretty_print( HtmlFragment('We permute rows %d and %d'%(m+1,c+1))) extended_matrix_as_latex(M) pivot[m] = k break a=M[m,k] for n in range(m+1,neqs): if M[n,k]!=0: pretty_print( HtmlFragment("We add %s times row %d to row %d"%(-M[n,k]/a, m+1, n+1))) M=M.with_added_multiple_of_row(n,m,-M[n,k]/a) extended_matrix_as_latex(M) A = M[:,:-1] b = M.column(-1) SLE_as_latex(A, b, variables) SEL_type = 'compatible' null_rows = None for k,(row,y) in enumerate(zip(A,b)): if row.is_zero(): if y==0 and null_rows is None: null_rows = k break elif y!=0: SEL_type = 'incompatible' if SEL_type == 'incompatible': pretty_print( HtmlFragment('The system has no solutions')) return if null_rows: pretty_print(HtmlFragment('We remove trivial 0=0 equations')) A = A[:null_rows,:] b = b[:null_rows] SLE_as_latex(A, b, variables) ifree_variables = [k for k in range(nvars) if k not in ibound_variables] bound_variables = [variables[k] for k in ibound_variables] free_variables = [variables[k] for k in ifree_variables] pretty_print( HtmlFragment('Free variables: %s'% free_variables)) pretty_print( HtmlFragment('Bound variables: %s'% bound_variables)) reduced_eqs = [ sum(c*v for c,v in zip(row, variables))==y for row,y in zip(A,b) ] xvector = vector(variables) if len(bound_variables)==1: soldict = solve(reduced_eqs, bound_variables[0], solution_dict=True)[0] else: soldict = solve(reduced_eqs, bound_variables, solution_dict=True)[0] pretty_print( HtmlFragment('Solution in parametric form')) parametric_sol = matrix( xvector.apply_map(lambda s:s.subs(soldict)) ).transpose() show(parametric_sol) pretty_print( HtmlFragment('Solution in vector form')) pretty_print( HtmlFragment( r'$$ %s + \left\langle %s\right\rangle$$'%( latex(parametric_sol.subs(dict(zip(free_variables, [0]*len(free_variables))))), ','.join(latex( parametric_sol.apply_map(lambda s:s.diff(v)) ) for v in free_variables) if free_variables else latex(matrix([0]*nvars).transpose())) )) pretty_print( HtmlFragment('Dimension is %d'%len(free_variables))) }}} {{attachment:NHSEL_1.png||width=600}} {{attachment:NHSEL_2.png||width=600}} |
Sage Interactions - Linear Algebra
goto interact main page
Contents
-
Sage Interactions - Linear Algebra
- Numerical instability of the classical Gram-Schmidt algorithm
- Equality of det(A) and det(A.tranpose())
- Linear transformations
- Gerschgorin Circle Theorem
- Singular value decomposition
- Discrete Fourier Transform
- The Gauss-Jordan method for inverting a matrix
- Solution of an homogeneous system of linear equations
- Solution of a non homogeneous system of linear equations
Numerical instability of the classical Gram-Schmidt algorithm
by Marshall Hampton

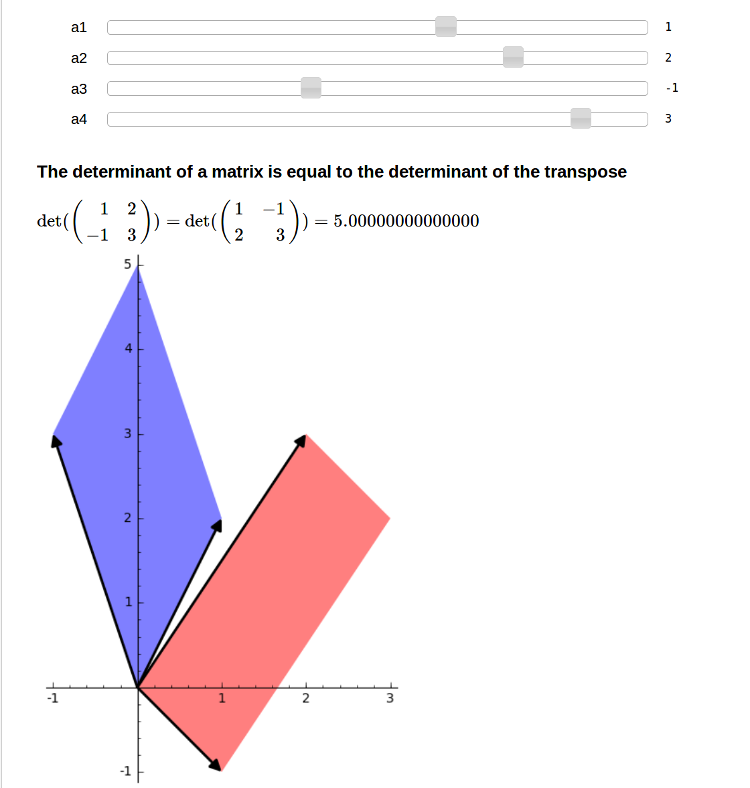
Equality of det(A) and det(A.tranpose())
by Marshall Hampton
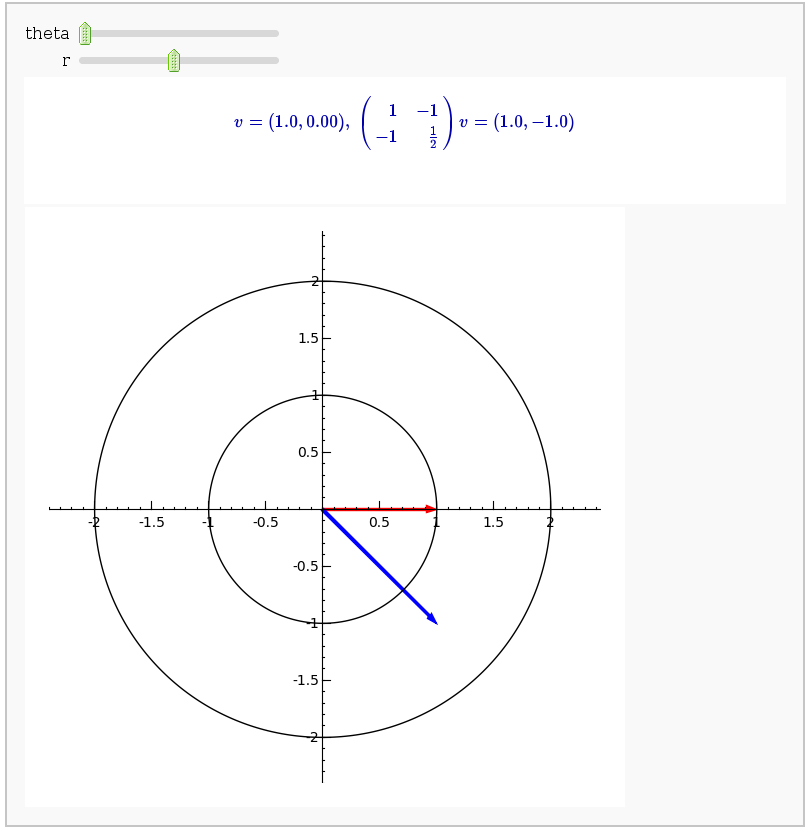
Linear transformations
by Jason Grout
A square matrix defines a linear transformation which rotates and/or scales vectors. In the interact command below, the red vector represents the original vector (v) and the blue vector represents the image w under the linear transformation. You can change the angle and length of v by changing theta and r.
Gerschgorin Circle Theorem
by Marshall Hampton. This animated version requires convert (imagemagick) to be installed, but it can easily be modified to a static version. The animation illustrates the idea behind the stronger version of Gerschgorin's theorem, which says that if the disks around the eigenvalues are disjoint then there is one eigenvalue per disk. The proof is by continuity of the eigenvalues under a homotopy to a diagonal matrix.

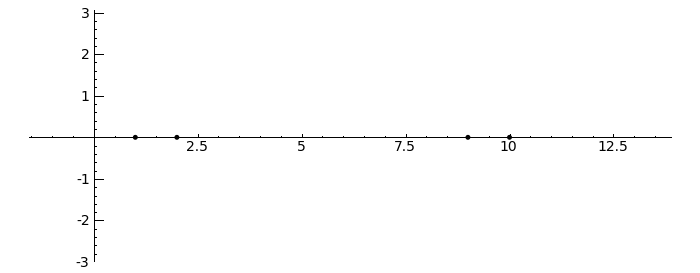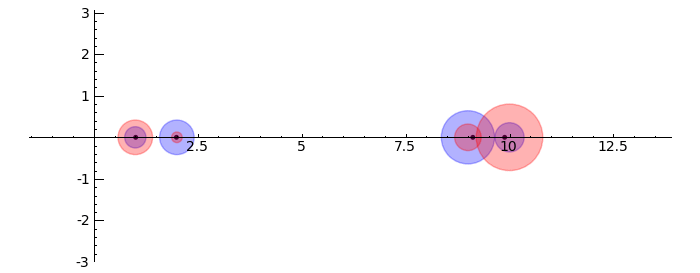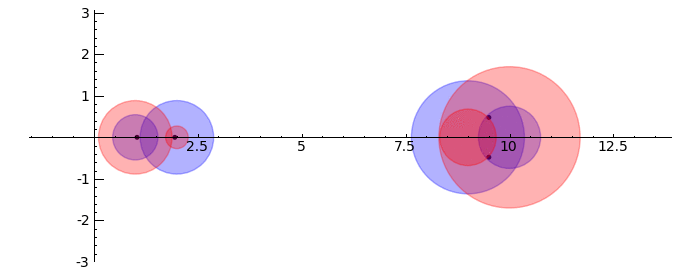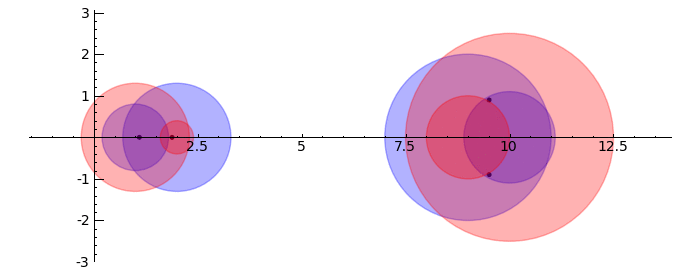
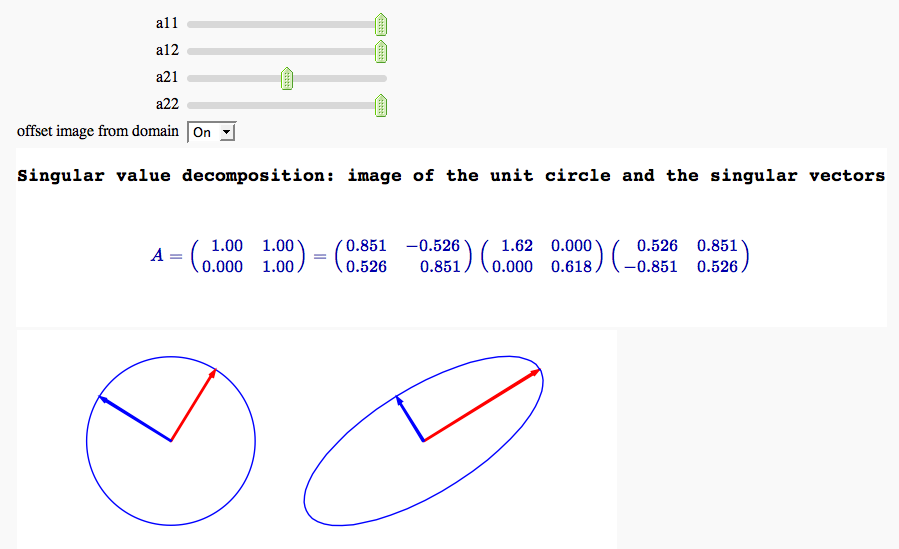
Singular value decomposition
by Marshall Hampton
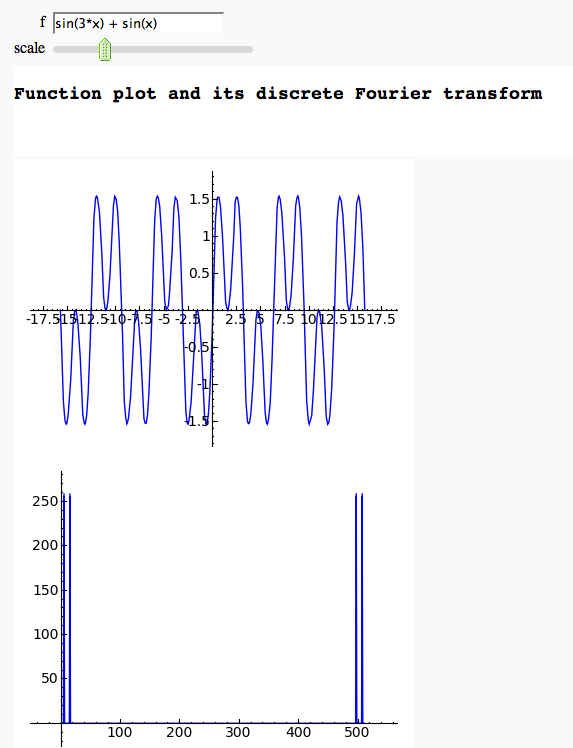
Discrete Fourier Transform
by Marshall Hampton
The Gauss-Jordan method for inverting a matrix
by Hristo Inouzhe
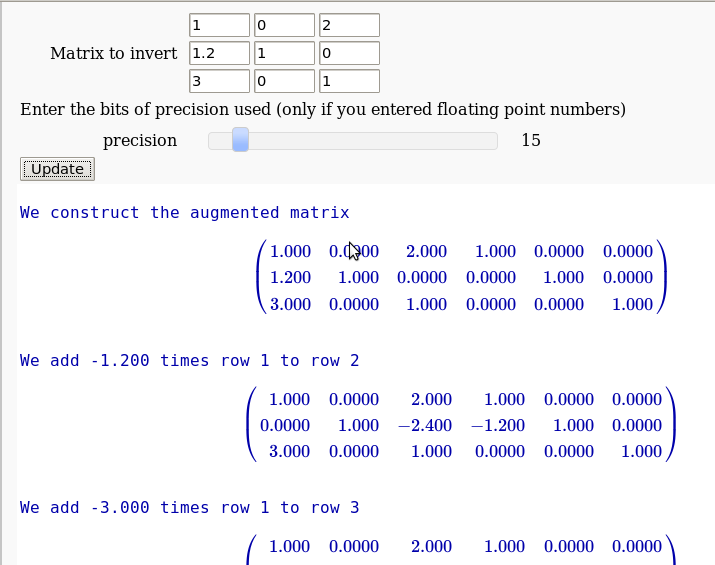
...(goes all the way to invert the matrix)
Solution of an homogeneous system of linear equations
by Pablo Angulo and Hristo Inouzhe
Coefficients are introduced as a matrix in a single text box. The number of equations and unknowns are arbitrary.


Solution of a non homogeneous system of linear equations
by Pablo Angulo and Hristo Inouzhe
Coefficients are introduced as a matrix in a single text box, and independent terms as a vector in a separate text box. The number of equations and unknowns are arbitrary.


