|
Size: 5314
Comment:
|
Size: 11255
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| goto [:interact:interact main page] == Numerical instability of the classical Gram-Schmidt algorithm == |
goto [[interact|interact main page]] <<TableOfContents>> == Numerical instability of the classical Gram-Schmidt algorithm FIXME == |
| Line 6: | Line 8: |
| {{{ | {{{#!sagecell |
| Line 60: | Line 62: |
| attachment:GramSchmidt.png | {{attachment:GramSchmidt.png}} == Equality of det(A) and det(A.tranpose()) == srg = srange(-4,4,1/10,include_endpoint=True) @interact def dualv(a1=slider(srg,default=1),a2=slider(srg,default=2), a3=slider(srg,default=-1),a4=slider(srg,default=3)): A1 = arrow2d([0,0],[a1,a2],rgbcolor='black') A2 = arrow2d([0,0],[a3,a4],rgbcolor='black') A3 = arrow2d([0,0],[a1,a3],rgbcolor='black') A4 = arrow2d([0,0],[a2,a4],rgbcolor='black') p1 = polygon([[0,0],[a1,a2],[a1+a3,a2+a4],[a3,a4],[0,0]], alpha=.5) p2 = polygon([[0,0],[a1,a3],[a1+a2,a3+a4],[a2,a4],[0,0]],rgbcolor='red', alpha=.5) A = matrix([[a1,a2],[a3,a4]]) html('<h3>The determinant of a matrix is equal to the determinant of the transpose</h3>') html("$det(%s) = det(%s)$"%(latex(A),latex(A.transpose()))) show(A1+A2+A3+A4+p1+p2) |
| Line 68: | Line 85: |
| {{{ @interact def linear_transformation(theta=slider(0, 2*pi, .1), r=slider(0.1, 2, .1, default=1)): A=matrix([[1,-1],[-1,1/2]]) |
{{{#!sagecell @interact def linear_transformation(A=matrix([[1,-1],[-1,1/2]]),theta=slider(0, 2*pi, .1), r=slider(0.1, 2, .1, default=1)): |
| Line 74: | Line 90: |
| circles = sum([circle((0,0), radius=i, rgbcolor=(0,0,0)) for i in [1..2]]) print jsmath("v = %s,\; %s v=%s"%(v.n(4),latex(A),w.n(4))) show(v.plot(rgbcolor=(1,0,0))+w.plot(rgbcolor=(0,0,1))+circles,aspect_ratio=1) }}} attachment:Linear-Transformations.png |
circles = sum([circle((0,0), radius=i, color='black') for i in [1..2]]) html("$%s %s=%s$"%tuple(map(latex, [A, v.column().n(4), w.column().n(4)]))) show(v.plot(color='red')+w.plot(color='blue')+circles,aspect_ratio=1) }}} {{attachment:Linear-Transformations.png}} == Gerschgorin Circle Theorem == by Marshall Hampton. This animated version requires convert (imagemagick) to be installed, but it can easily be modified to a static version. The animation illustrates the idea behind the stronger version of Gerschgorin's theorem, which says that if the disks around the eigenvalues are disjoint then there is one eigenvalue per disk. The proof is by continuity of the eigenvalues under a homotopy to a diagonal matrix. {{{#!sagecell from scipy import linalg html('<h2>The Gerschgorin circle theorem</h2>') @interact def Gerschgorin(Ain = input_box(default='[[10,1,1/10,0],[-1,9,0,1],[1,0,2,3/10],[-.5,0,-.3,1]]', type = str, label = 'A = '), an_size = slider(1,100,1,1.0)): A = sage_eval(Ain) size = len(A) html('$A = ' + latex(matrix(RealField(10),A))+'$') A = matrix(RealField(10),A) B = [[0 for i in range(size)] for j in range(size)] for i in range(size): B[i][i] = A[i][i] B = matrix(B) frames = [] centers = [(real(q),imag(q)) for q in [A[i][i] for i in range(size)]] radii_row = [sum([abs(A[i][j]) for j in range(i)+range(i+1,size)]) for i in range(size)] radii_col = [sum([abs(A[j][i]) for j in range(i)+range(i+1,size)]) for i in range(size)] x_min = min([centers[i][0]-radii_row[i] for i in range(size)]+[centers[i][0]-radii_col[i] for i in range(size)]) x_max = max([centers[i][0]+radii_row[i] for i in range(size)]+[centers[i][0]+radii_col[i] for i in range(size)]) y_min = min([centers[i][1]-radii_row[i] for i in range(size)]+[centers[i][1]-radii_col[i] for i in range(size)]) y_max = max([centers[i][1]+radii_row[i] for i in range(size)]+[centers[i][1]+radii_col[i] for i in range(size)]) if an_size > 1: t_range= srange(0,1+1/an_size,1/an_size) else: t_range = [1] for t in t_range: C = t*A + (1-t)*B eigs = [CDF(x) for x in linalg.eigvals(C.numpy())] eigpoints = points([(real(q),imag(q)) for q in eigs],pointsize = 10, rgbcolor = (0,0,0)) centers = [(real(q),imag(q)) for q in [A[i][i] for i in range(size)]] radii_row = [sum([abs(C[i][j]) for j in range(i)+range(i+1,size)]) for i in range(size)] radii_col = [sum([abs(C[j][i]) for j in range(i)+range(i+1,size)]) for i in range(size)] scale = max([(x_max-x_min),(y_max-y_min)]) scale = 7/scale row_circles = sum([circle(centers[i],radii_row[i],fill=True, alpha = .3) for i in range(size)]) col_circles = sum([circle(centers[i],radii_col[i],fill=True, rgbcolor = (1,0,0), alpha = .3) for i in range(size)]) ft = eigpoints+row_circles+col_circles frames.append(ft) show(animate(frames,figsize = [(x_max-x_min)*scale,(y_max-y_min)*scale], xmin = x_min, xmax=x_max, ymin = y_min, ymax = y_max)) }}} {{attachment:Gerschanimate.png}} {{attachment:Gersch.gif}} |
| Line 82: | Line 147: |
| {{{ | {{{#!sagecell |
| Line 89: | Line 154: |
| def svd_vis(a11=slider(-1,1,.05,1),a12=slider(-1,1,.05,1),a21=slider(-1,1,.05,0),a22=slider(-1,1,.05,1),ofs= selector(['Off','On'],label='offset image from domain')): | def svd_vis(a11=slider(-1,1,.05,1),a12=slider(-1,1,.05,1),a21=slider(-1,1,.05,0),a22=slider(-1,1,.05,1),ofs= ('offset image from domain',False)): |
| Line 93: | Line 158: |
| if ofs == 'On': | if ofs: |
| Line 106: | Line 171: |
| print jsmath("A = %s = %s %s %s"%(latex(my_mat), latex(matrix(rf_low,u.tolist())), latex(matrix(rf_low,2,2,[s[0],0,0,s[1]])), latex(matrix(rf_low,vh.tolist())))) image_ell = parametric_plot(rotell(s,u,t, offset),0,2*pi) |
html("$A = %s = %s %s %s$"%(latex(my_mat), latex(matrix(rf_low,u.tolist())), latex(matrix(rf_low,2,2,[s[0],0,0,s[1]])), latex(matrix(rf_low,vh.tolist())))) image_ell = parametric_plot(rotell(s,u,t, offset),(0,2*pi)) |
| Line 110: | Line 175: |
| show(graph_stuff,frame = False,axes=False,figsize=[fsize,fsize]) }}} attachment:svd1.png |
show(graph_stuff,frame = False,axes=False,figsize=[fsize,fsize])}}} {{attachment:svd1.png}} |
| Line 116: | Line 180: |
| {{{ | {{{#!sagecell |
| Line 120: | Line 184: |
| var('x') | |
| Line 124: | Line 187: |
| show(plot(f, pbegin, pend, plot_points = 512), figsize = [4,3]) f_vals = [f(ind) for ind in srange(pbegin, pend,(pend-pbegin)/512.0)] |
show(plot(f, (x,pbegin, pend), plot_points = 512), figsize = [4,3]) f_vals = [f(x=ind) for ind in srange(pbegin, pend,(pend-pbegin)/512.0)] |
| Line 127: | Line 190: |
| show(list_plot([abs(x) for x in my_fft], plotjoined=True), figsize = [4,3]) }}} attachment:dfft1.png |
show(list_plot([abs(i) for i in my_fft], plotjoined=True), figsize = [4,3]) }}} {{attachment:dfft1.png}} == The Gauss-Jordan method for inverting a matrix == by Hristo Inouzhe {{{#!sagecell #Choose the size D of the square matrix: D = 3 example = [[1 if k==j else 0 for k in range(D)] for j in range(D)] example[0][-1] = 2 example[-1][0] = 3 @interact def _(M=input_grid(D,D, default = example, label='Matrix to invert', to_value=matrix), tt = text_control('Enter the bits of precision used' ' (only if you entered floating point numbers)'), precision = slider(5,100,5,20), auto_update=False): if det(M)==0: print 'Failure: Matrix is not invertible' return if M.base_ring() == RR: M = M.apply_map(RealField(precision)) N=M M=M.augment(identity_matrix(D)) print 'We construct the augmented matrix' show(M) for m in range(0,D-1): if M[m,m] == 0: lista = [(M[j,m],j) for j in range(m,D)] maxi, c = max(lista) M[c,:],M[m,:]=M[m,:],M[c,:] print 'We permute rows %d and %d'%(m+1,c+1) show(M) for n in range(m+1,D): a=M[m,m] if M[n,m]!=0: print "We add %s times row %d to row %d"%(-M[n,m]/a, m+1, n+1) M=M.with_added_multiple_of_row(n,m,-M[n,m]/a) show(M) for m in range(D-1,-1,-1): for n in range(m-1,-1,-1): a=M[m,m] if M[n,m]!=0: print "We add %s times row %d to the row %d"%(-M[n,m]/a, m+1, n+1) M=M.with_added_multiple_of_row(n,m,-M[n,m]/a) show(M) for m in range(0,D): if M[m,m]!=1: print 'We divide row %d by %s'%(m+1,M[m,m]) M = M.with_row_set_to_multiple_of_row(m,m,1/M[m,m]) show(M) M=M.submatrix(0,D,D) print 'We keep the right submatrix, which contains the inverse' html('$$M^{-1}=%s$$'%latex(M)) print 'We check it actually is the inverse' html('$$M^{-1}*M=%s*%s=%s$$'%(latex(M),latex(N),latex(M*N))) }}} {{attachment:gauss-jordan.png}} ...(goes all the way to invert the matrix) |
Sage Interactions - Linear Algebra
goto interact main page
Contents
Numerical instability of the classical Gram-Schmidt algorithm FIXME
by Marshall Hampton (tested by William Stein, who thinks this is really nice!)

Equality of det(A) and det(A.tranpose())
srg = srange(-4,4,1/10,include_endpoint=True) @interact def dualv(a1=slider(srg,default=1),a2=slider(srg,default=2), a3=slider(srg,default=-1),a4=slider(srg,default=3)):
- A1 = arrow2d([0,0],[a1,a2],rgbcolor='black') A2 = arrow2d([0,0],[a3,a4],rgbcolor='black') A3 = arrow2d([0,0],[a1,a3],rgbcolor='black') A4 = arrow2d([0,0],[a2,a4],rgbcolor='black')
p1 = polygon(0,0],[a1,a2],[a1+a3,a2+a4],[a3,a4],[0,0, alpha=.5) p2 = polygon(0,0],[a1,a3],[a1+a2,a3+a4],[a2,a4],[0,0,rgbcolor='red', alpha=.5) A = matrix(a1,a2],[a3,a4) html('<h3>The determinant of a matrix is equal to the determinant of the transpose</h3>') html("det(%s) = det(%s)"%(latex(A),latex(A.transpose()))) show(A1+A2+A3+A4+p1+p2)
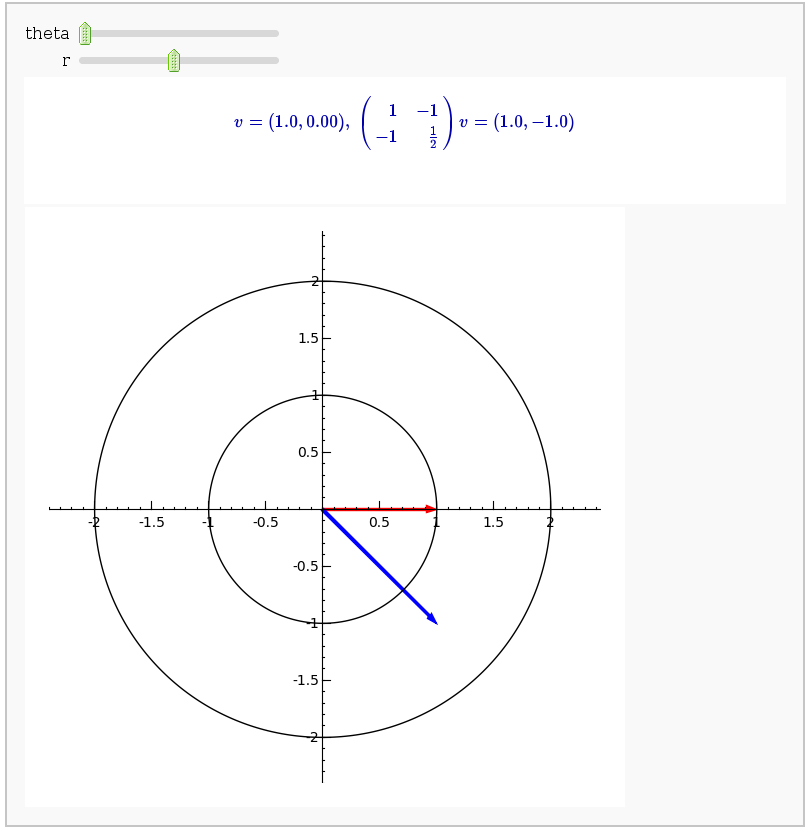
Linear transformations
by Jason Grout
A square matrix defines a linear transformation which rotates and/or scales vectors. In the interact command below, the red vector represents the original vector (v) and the blue vector represents the image w under the linear transformation. You can change the angle and length of v by changing theta and r.
Gerschgorin Circle Theorem
by Marshall Hampton. This animated version requires convert (imagemagick) to be installed, but it can easily be modified to a static version. The animation illustrates the idea behind the stronger version of Gerschgorin's theorem, which says that if the disks around the eigenvalues are disjoint then there is one eigenvalue per disk. The proof is by continuity of the eigenvalues under a homotopy to a diagonal matrix.

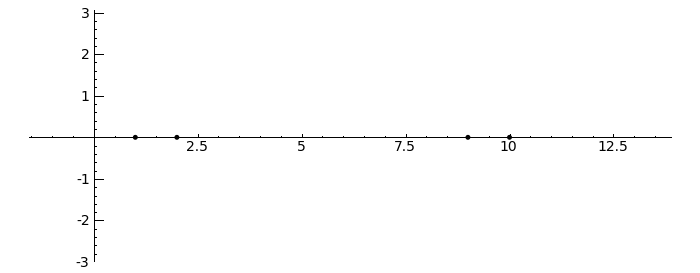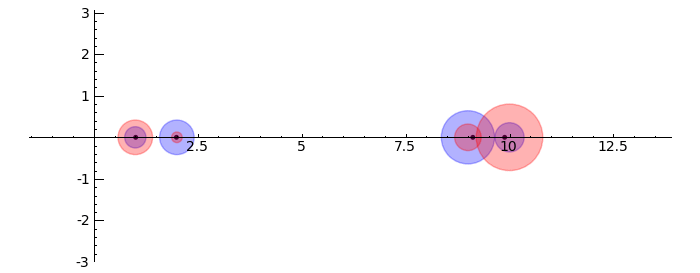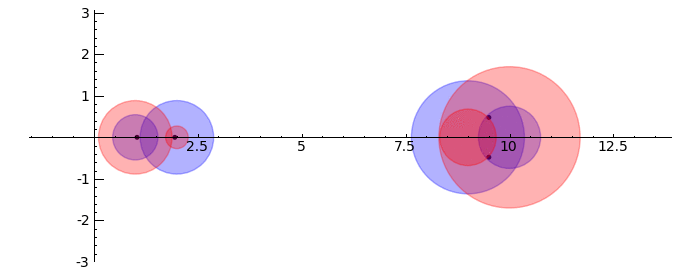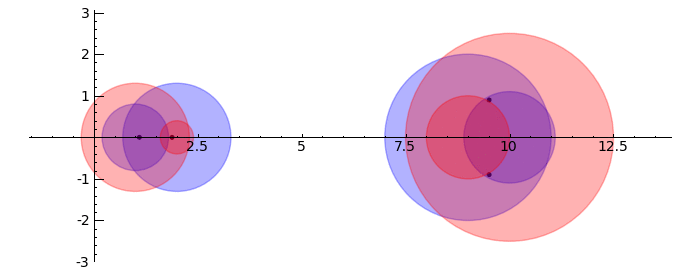
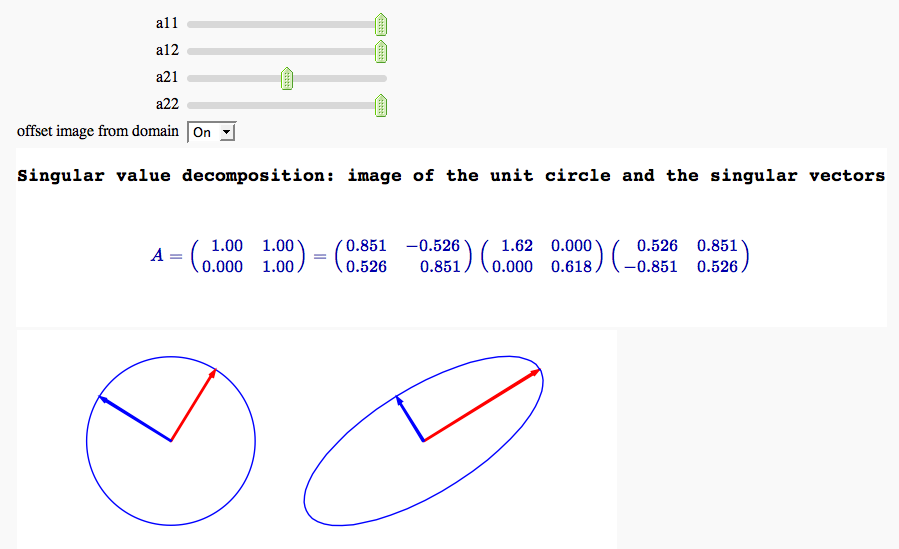
Singular value decomposition
by Marshall Hampton
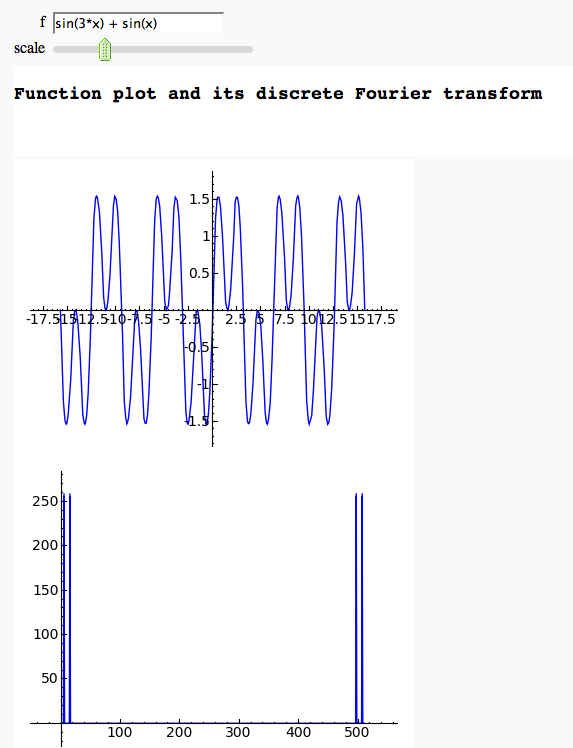
Discrete Fourier Transform
by Marshall Hampton
The Gauss-Jordan method for inverting a matrix
by Hristo Inouzhe
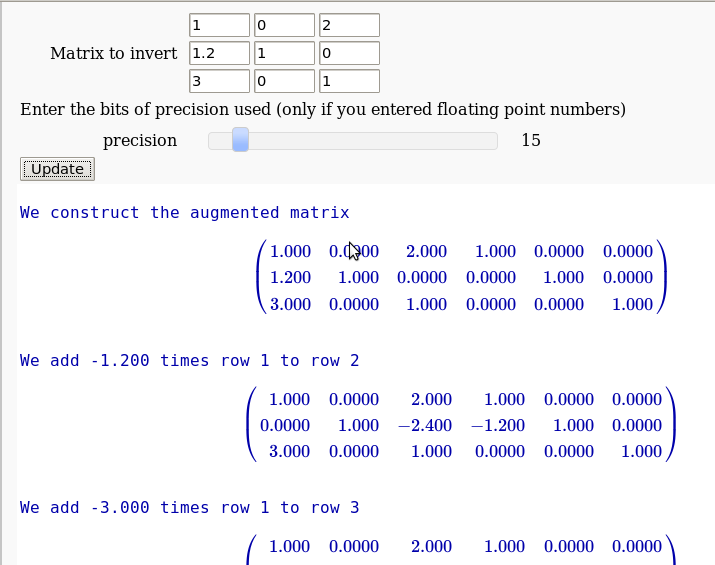
...(goes all the way to invert the matrix)
