|
Size: 1513
Comment:
|
Size: 18327
Comment: fixing geodesics interact ...
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 6: | Line 6: |
| == Intersecting tetrahedral reflections == | == Intersecting tetrahedral reflections FIXME == |
| Line 8: | Line 8: |
| {{{ | {{{#!sagecell #Pairs of tetrahedra, one the reflection of the other in the internal face, are joined by union operations: |
| Line 11: | Line 12: |
| p12 = p1.union(p2) | p12 = p1.convex_hull(p2) |
| Line 14: | Line 15: |
| p34 = p3.union(p4) | p34 = p3.convex_hull(p4) |
| Line 17: | Line 18: |
| p56 = p5.union(p6) | p56 = p5.convex_hull(p6) |
| Line 20: | Line 21: |
| p78 = p7.union(p8) | p78 = p7.convex_hull(p8) |
| Line 23: | Line 24: |
| def tetra_plot(opac = slider(srange(0,1.0,float(.01)), default = float(.25))): print opac |
def tetra_plot(opac = slider(srange(0,1.0,.25), default = .25)): |
| Line 33: | Line 33: |
== Evolutes == by Pablo Angulo. Computes the evolute of a plane curve given in parametric coordinates. The curve must be parametrized from the interval [0,2pi]. {{{#!sagecell var('t'); def norma(v): return sqrt(sum(x^2 for x in v)) paso_angulo=5 @interact def _( gamma1=input_box(default=sin(t)), gamma2=input_box(default=1.3*cos(t)), draw_normal_lines=True, rango_angulos=range_slider(0,360,paso_angulo,(0,90),label='Draw lines for these angles'), draw_osculating_circle=True, t0=input_box(default=pi/3,label='parameter value for the osculating circle'), auto_update=False ): gamma=(gamma1,gamma2) gammap=(gamma[0].derivative(),gamma[1].derivative()) np=norma(gammap) gammapp=(gammap[0].derivative(),gammap[1].derivative()) npp=norma(gammapp) normal=(gammap[1]/np, -gammap[0]/np) curvatura=(gammap[1]*gammapp[0]-gammap[0]*gammapp[1])/norma(gammap)^3 radio=1/curvatura centros=(gamma[0]+radio*normal[0],gamma[1]+radio*normal[1]) curva=parametric_plot(gamma,(t,0,2*pi)) evoluta=parametric_plot(centros,(t,0,2*pi), color='red') grafica=curva+evoluta if draw_normal_lines: f=2*pi/360 lineas=sum(line2d( [ (gamma[0](t=i*f), gamma[1](t=i*f)), (centros[0](t=i*f), centros[1](t=i*f)) ], thickness=1,rgbcolor=(1,0.8,0.8)) for i in range(rango_angulos[0], rango_angulos[1]+paso_angulo, paso_angulo)) grafica+=lineas if draw_osculating_circle and 0<t0<2*pi: punto=point((gamma[0](t=t0), gamma[1](t=t0)), rgbcolor=hue(0),pointsize=30) circulo=circle( (centros[0](t=t0), centros[1](t=t0)), radio(t=t0) ) grafica+=punto+circulo show(grafica,aspect_ratio=1,xmin=-2,xmax=2,ymin=-2,ymax=2) }}} {{attachment:evoluta3.png}} == Geodesics on a parametric surface == by Antonio Valdés and Pablo Angulo. This example was originally composed of two interacts: - the first allowing the user to introduce a parametric surface, and draw it. - the second drawing a geodesic within the surface. The separation was so that after the first interact, the geodesic equations were "compiled", thus making the second interact faster. This still looks as a good idea to me, so please read the original code at https://malabares.cancamusa.net/home/pub/14/ But the following is fixed so that there is only one interact, and sagecell works. There might be another way yto {{{#!sagecell from scipy.integrate import odeint u, v, t, du, dv = var('u v t du dv') def fading_line3d(points, rgbcolor1, rgbcolor2, *args, **kwds): L = len(points) vcolor1 = vector(RDF, rgbcolor1) vcolor2 = vector(RDF, rgbcolor2) return sum(line3d(points[j:j+2], rgbcolor = tuple( ((L-j)/L)*vcolor1 + (j/L)*vcolor2 ), *args, **kwds) for j in srange(L-1)) steps = 100 @interact def _(x = input_box(3*sin(u)*cos(v), 'x'), y = input_box(sin(u)*sin(v), 'y'), z = input_box(2*cos(u), 'z'), int_u = input_grid(1, 2, default = [[0,pi]], label = 'u -interval'), int_v = input_grid(1, 2, default = [[-pi,pi]], label = 'v -interval'), init_point = input_grid(1, 2, default = [[-pi/4,pi/8]], label = 'coordinates of \ninitial point'), init_vector = input_grid(1, 2, default = [[1,0]], label = 'coordinates of \ninitial vector'), int_s = slider(0, 10, 1/10, default = pi/2, label = 'geodesic interval'), sliding_color = checkbox(True,'change color along the geodesic')): int_u = int_u[0] int_v = int_v[0] u_0, v_0 = init_point[0] V_u, V_v = init_vector[0] F = vector([x, y, z]) S_plot = parametric_plot3d( F, (u, int_u[0], int_u[1]), (v, int_v[0], int_v[1])) dFu = F.diff(u) dFv = F.diff(v) Fu = fast_float(dFu, u, v) Fv = fast_float(dFv, u, v) ufunc = function('ufunc', t) vfunc = function('vfunc', t) dFtt = F(u=ufunc, v=vfunc).diff(t, t) ec1 = dFtt.dot_product(dFu(u=ufunc, v=vfunc)) ec2 = dFtt.dot_product(dFv(u=ufunc, v=vfunc)) dv, ddv, du, ddu = var('dv, ddv, du, ddu') diffec1 = ec1.subs_expr(diff(ufunc, t) == du, diff(ufunc, t, t) == ddu, diff(vfunc, t) == dv, diff(vfunc, t, t) == ddv, ufunc == u, vfunc == v) diffec2 = ec2.subs_expr(diff(ufunc, t) == du, diff(ufunc, t, t) == ddu, diff(vfunc, t) == dv, diff(vfunc, t, t) == ddv, ufunc == u, vfunc == v) sols = solve([diffec1 == 0 , diffec2 == 0], ddu, ddv) ddu_rhs = (sols[0][0]).rhs().full_simplify() ddv_rhs = (sols[0][1]).rhs().full_simplify() ddu_ff = fast_float(ddu_rhs, du, dv, u, v) ddv_ff = fast_float(ddv_rhs, du, dv, u, v) def func(y,t): v = list(y) return [ddu_ff(*v), ddv_ff(*v), v[0], v[1]] Point = [u_0, v_0] velocity = [V_u, V_v] Point = map(float, Point) velocity = map(float, velocity) geo2D_aux = odeint(func, y0 = [velocity[0], velocity[1], Point[0], Point[1]], t = srange(0, int_s, 0.01)) geo3D = [F(u=l,v=r) for [j, k, l, r] in geo2D_aux] if sliding_color: g_plot = fading_line3d(geo3D, rgbcolor1 = (1, 0, 0), rgbcolor2 = (0, 1, 0), thickness=4) else: g_plot = line3d(geo3D, rgbcolor=(0, 1, 0), thickness=4) P = F(u=Point[0], v=Point[1]) P_plot = point3d((P[0], P[1], P[2]), rgbcolor = (0, 0, 0), pointsize = 30) V = velocity[0] * Fu(u = Point[0], v = Point[1]) + \ velocity[1] * Fv(u= Point[0], v = Point[1]) V_plot = arrow3d(P, P + V, color = 'black') show(g_plot + S_plot + V_plot + P_plot,aspect_ratio = [1, 1, 1]) }}} {{attachment:geodesics1.png}} {{attachment:geodesics2.png}} == Dimensional Explorer == By Eviatar Bach Renders 2D images (perspective or spring-layout) and 3D models of 0-10 dimensional hypercubes. It also displays number of edges and vertices. {{{#!sagecell @interact def render(Display=selector(['2D Perspective', '2D Spring-layout', '3D']), Dimension=slider(0,10,default=4, step_size=1), Size=slider(0,10,default=5,step_size=1), Vertices=False, Calculations=False): if Display=='2D Perspective': if Dimension==0: g=graphs.GridGraph([1]) print 'Vertices:', len(g.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(g.edges()), ('(%s*(%s/2))' %(len(g.vertices()), Dimension) if Calculations else '') g.show(figsize=[Size,Size], vertex_size=30, vertex_labels=False, transparent=True, vertex_colors='black') else: g=graphs.CubeGraph(Dimension) print 'Vertices:', len(g.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(g.edges()), ('(%s*(%s/2))' %(len(g.vertices()), Dimension) if Calculations else '') g.show(figsize=[Size,Size], vertex_size=(20 if Vertices else 0), vertex_labels=False, transparent=True, vertex_colors='black') if Display=='2D Spring-layout': if Dimension==0: s=graphs.GridGraph([1]) print 'Vertices:', len(s.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(s.edges()), ('(%s*(%s/2))' %(len(s.vertices()), Dimension) if Calculations else '') s.show(figsize=[Size,Size], vertex_size=30, vertex_labels=False, transparent=True, vertex_colors='black') else: s=graphs.GridGraph([2]*Dimension) print 'Vertices:', len(s.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(s.edges()), ('(%s*(%s/2))' %(len(s.vertices()), Dimension) if Calculations else '') s.show(figsize=[Size,Size], vertex_size=(20 if Vertices else 0), vertex_labels=False, transparent=True, vertex_colors='black') if Display=='3D': if Dimension==0: d=graphs.GridGraph([1]) print 'Vertices:', len(d.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(d.edges()), ('(%s*(%s/2))' %(len(d.vertices()), Dimension) if Calculations else '') d.show3d(figsize=[Size/2,Size/2], vertex_size=0.001) else: d=graphs.CubeGraph(Dimension) print 'Vertices:', len(d.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(d.edges()), ('(%s*(%s/2))' %(len(d.vertices()), Dimension) if Calculations else '') d.show3d(figsize=[Size,Size], vertex_size=(0.03 if Vertices else 0.001)) }}} {{attachment:dimensions.png}} == Crofton's formula == by Pablo Angulo. Illustrates [[http://en.wikipedia.org/wiki/Crofton%27s_formula| Crofton's formula]] by throwing some random lines and computing the intersection number with a given curve. May use either solve for exact computation of the intersections, or may also approximate the curve by straight segments (this is the default). {{{#!sagecell from collections import defaultdict var('t x y') pin = pi.n() def longitud(curva, t0, t1): dxdt = derivative(curva[0], t) dydt = derivative(curva[1], t) integrando(t) = sqrt(dxdt^2 + dydt^2) i,_ = numerical_integral(integrando, t0, t1) return i def random_line(cota): theta = random()*pin k = 2*cota*random() - cota return sin(theta)*x + cos(theta)*y + k def crofton_exact(curva, t0, t1, L, M): forget() assume(t>t0) assume(t<t1) pp = parametric_plot(curva, (t, t0, t1), color='red') cortesd = defaultdict(int) for k in range(L): rl = random_line(M) ss = solve(rl(x=curva[0], y=curva[1]), t) cortes = 0 for s in ss: tt = s.rhs() x0,y0 = curva[0](t=tt), curva[1](t=tt) if x0 in RR and y0 in RR: pp += point2d((x0,y0), pointsize = 30) cortes += 1 if cortes: pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='green') else: pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='blue') cortesd[cortes] += 1 return cortesd, pp def random_line_n(cota): theta = random()*pin k = 2*cota*random() - cota return sin(theta), cos(theta), k def interseccion_sr(punto1, punto2, recta): 'Devuelve el punto de interseccion de una recta y un segmento, o None si no se cortan' x1, y1 = punto1 x2, y2 = punto2 a, b, c = recta num = (-c - a*x1 - b*y1) den = (a*(x2 - x1) + b*(y2 - y1)) if (0 < num < den) or (den < num < 0): t_i = num/den return ((1-t_i)*x1 + t_i*x2, (1-t_i)*y1 + t_i*y2) else: return None def interseccion_cr(curva, t0, t1, recta, partes=50): '''Devuelve el numero de puntos de interseccion de una curva y una recta''' x,y = curva paso = (t1 - t0)/partes puntos = [(x(t=tr), y(t=tr)) for tr in srange(t0, t1 + paso, paso)] intersecciones = (interseccion_sr(puntos[j], puntos[j+1], recta) for j in xrange(partes-1)) return [p for p in intersecciones if p ] def crofton_aprox(curva, t0, t1, L, M): cortesd = defaultdict(int) pp = parametric_plot(curva, (t, t0, t1), color='red') for k in range(L): a,b,c = random_line_n(M) rl = a*x + b*y + c cortes = interseccion_cr(curva, t0, t1, (a,b,c)) if cortes: pp += sum(point2d(p, pointsize = 30) for p in cortes) pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='green') else: pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='blue') cortesd[len(cortes)] += 1 return cortesd, pp def print_stats(d): print 'Number of lines with k intersection points:' print ', '.join('%d:%d'%(k,v) for k,v in d.iteritems()) @interact def crofton_interact(u1 = text_control('x and y coordinates of curve'), curvax = input_box(t^2, label='x(t)' ), curvay = input_box(2*t-1, label='y(t)' ), u2 = text_control('Interval of definition'), t0 = 0, t1 = 1, u3 = text_control('Draw L lines randomly cos(t)x + sin(t)y + K, |K|<M, 0 <= t < 2pi'), M = 2, L = 5, u4 = text_control('Use function "solve" from maxima for exact computations?'), exact = checkbox(False), u5 = text_control('Otherwise, a curve is approximated by how many segments?'), steps = slider(4, 40, 4, 8)): if exact: cortesd, p = crofton_exact((curvax, curvay), t0, t1, L, M) else: cortesd, p = crofton_aprox((curvax, curvay), t0, t1, L, M) p.show(aspect_ratio=1, xmin=-2, xmax=2, ymin=-2,ymax=2) print 'A curve of lenght %f'%longitud((curvax, curvay), t0, t1) print_stats(cortesd) cortes_tot = sum(k*v for k,v in cortesd.iteritems()) print 'Approx length using Crofton\'s formula: %f'%((cortes_tot/L)*(pi*M)) }}} {{attachment:crofton4.png}} == Banchoff-Pohl area == by Pablo Angulo. Computes the Banchoff-Pohl "area enclosed by a spatial curve", by throwing some random lines and computing the linking number with the given curve. Lines not linked to the given curve are displayed in red, linked lines are displayed in green. {{{#!sagecell from collections import defaultdict var('t') a = 0; b= 2*pi def random_line3d(bound): '''Random line in R^3: first choose the guiding vector of the line, then choose a point in the plane p perpendicular to that vector. ''' p = vector([(2*random() - 1) for _ in range(3)]) v = p/norm(p) v2, v3 = matrix(v).right_kernel().basis() if det(matrix([v, v2, v3]))<0: v2, v3 = v3, v2 v2 = v2/norm(v2) v3 = v3 - (v3*v2)*v2 v3 = v3/norm(v3) return v, (2*random()*bound - bound, v2), (2*random()*bound - bound, v3) def winding_number(x, y, x0, y0): x -= x0 y -= y0 r2 = x^2 + y^2 xp = x.derivative(t) yp = y.derivative(t) integrando(t) = (x*yp -y*xp)/r2 i,e = numerical_integral(integrando, a, b) return round(i/(2*pi)) def linking_number(curve, line): v, (a2, v2), (a3, v3) = line M = matrix([v, v2, v3]) # curve2d = (curve*M.inverse())[1:] #This is VERY slow, for some reason! curve2d = sum(c*v for c,v in zip(curve,M.inverse()))[1:] x, y = curve2d return winding_number(x, y, a2,a3) def color_ln(number): if number: return (0,1-1/(1+number),0) else: return (1,0,0) def banchoff_pohl(curve, L, M): ln_d = defaultdict(int) pp = parametric_plot3d(curve, (t,0,2*pi), thickness=2) for k in range(L): a_line = random_line3d(M) ln = abs(linking_number(curve, a_line)) v, (l1, v1), (l2, v2) = a_line pp += parametric_plot3d(l1*v1+l2*v2+t*v,(t,-2,2), color=color_ln(ln)) ln_d[ln] += 1 return ln_d, pp def print_stats(d): print 'Number of lines with linking number k:' print ', '.join('%d:%d'%(k,v) for k,v in d.iteritems()) @interact def bp_interact( u1 = text_control('x, y, z coordinates of a closed space curve in [0,2*pi]'), curvax = input_box(cos(t), label='x(t)' ), curvay = input_box(sin(t), label='y(t)' ), curvaz = input_box(0, label='y(t)' ), u2 = text_control('The curve should be contained in a ball of radius M'), M = 1, u3 = text_control('Use L lines chosen randomly'), L = 10): ln_d, p = banchoff_pohl(vector((curvax, curvay, curvaz)), L, M) p.show(aspect_ratio=1, xmin=-2, xmax=2, ymin=-2,ymax=2) bp_area_aprox = (sum(k^2*v for k,v in ln_d.iteritems())/L)*2*pi*M^2 print 'Bahnchoff-Pohl area of the curve(aprox): %f'%bp_area_aprox print_stats(ln_d) }}} {{attachment:banchoff-pohl.png}} |
Sage Interactions - Geometry
goto interact main page
Contents
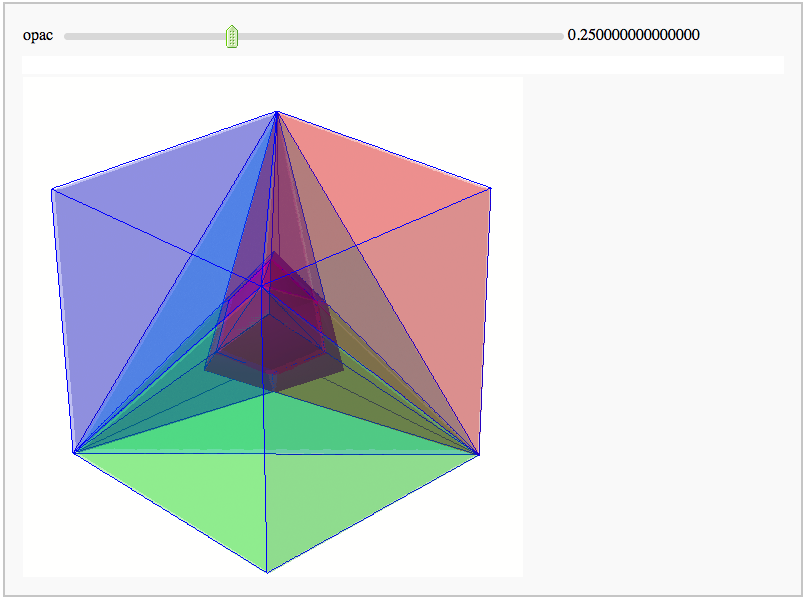
Intersecting tetrahedral reflections FIXME
by Marshall Hampton. Inspired by a question from Hans Schepker of Glass Geometry.
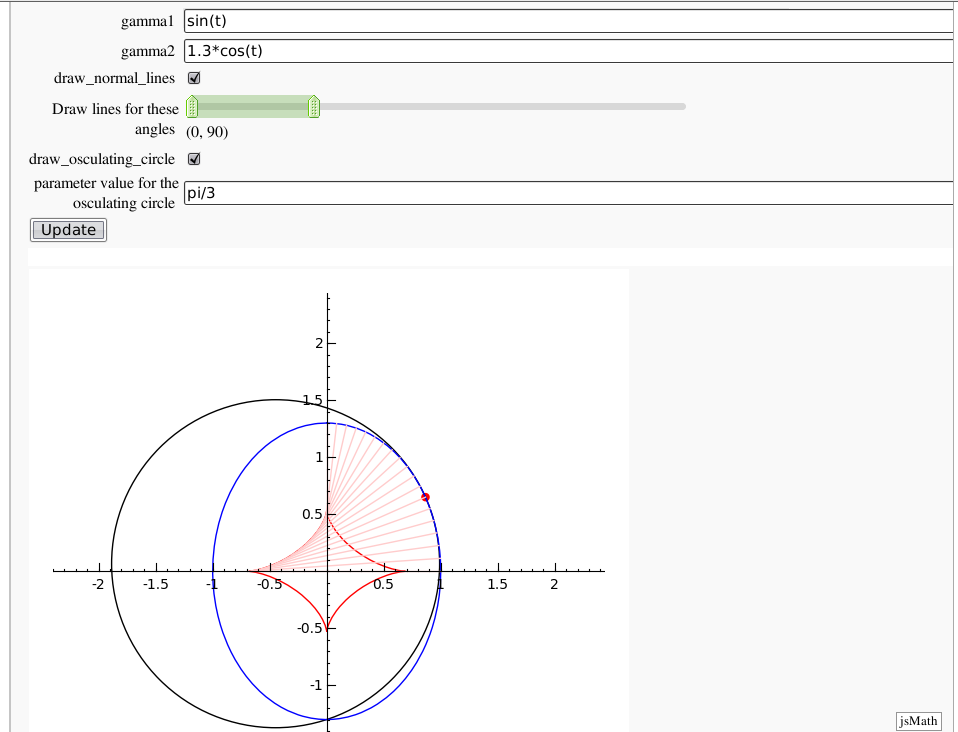
Evolutes
by Pablo Angulo. Computes the evolute of a plane curve given in parametric coordinates. The curve must be parametrized from the interval [0,2pi].
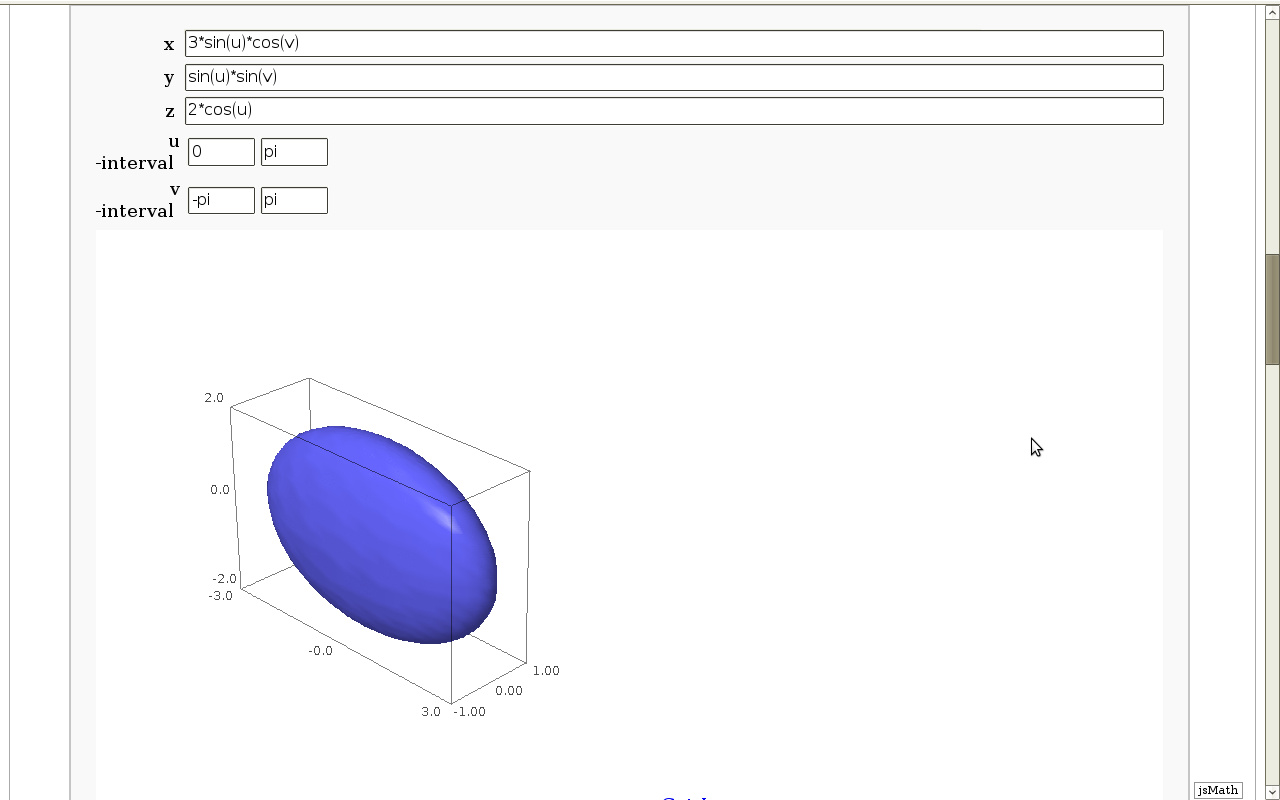
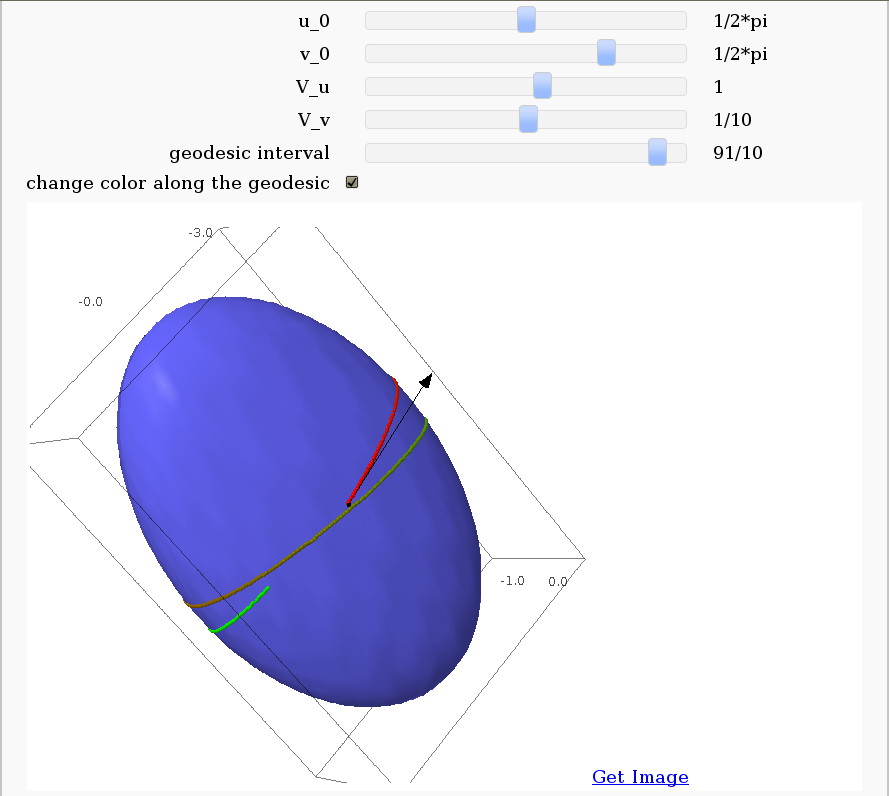
Geodesics on a parametric surface
by Antonio Valdés and Pablo Angulo. This example was originally composed of two interacts:
- - the first allowing the user to introduce a parametric surface, and draw it. - the second drawing a geodesic within the surface.
The separation was so that after the first interact, the geodesic equations were "compiled", thus making the second interact faster.
This still looks as a good idea to me, so please read the original code at https://malabares.cancamusa.net/home/pub/14/ But the following is fixed so that there is only one interact, and sagecell works. There might be another way yto
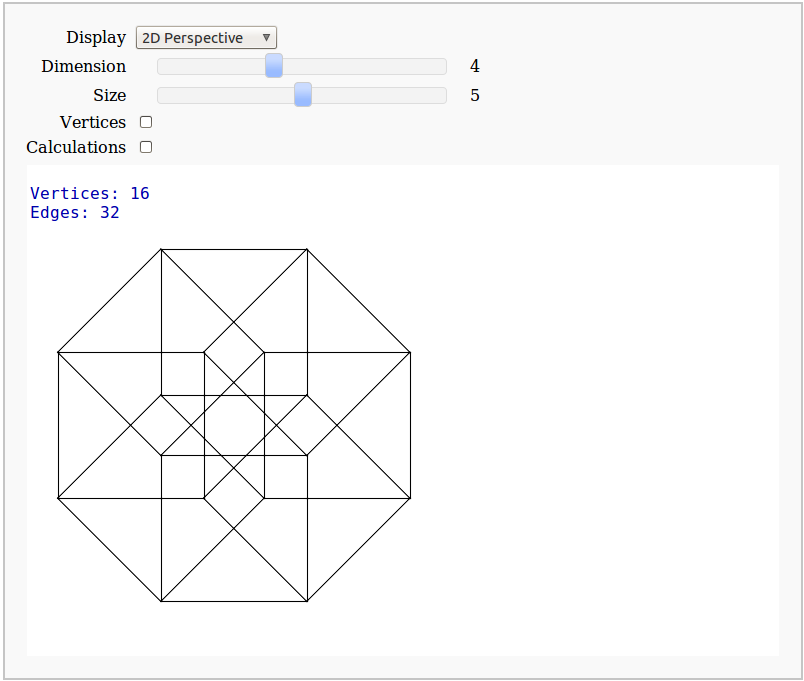
Dimensional Explorer
By Eviatar Bach
Renders 2D images (perspective or spring-layout) and 3D models of 0-10 dimensional hypercubes. It also displays number of edges and vertices.
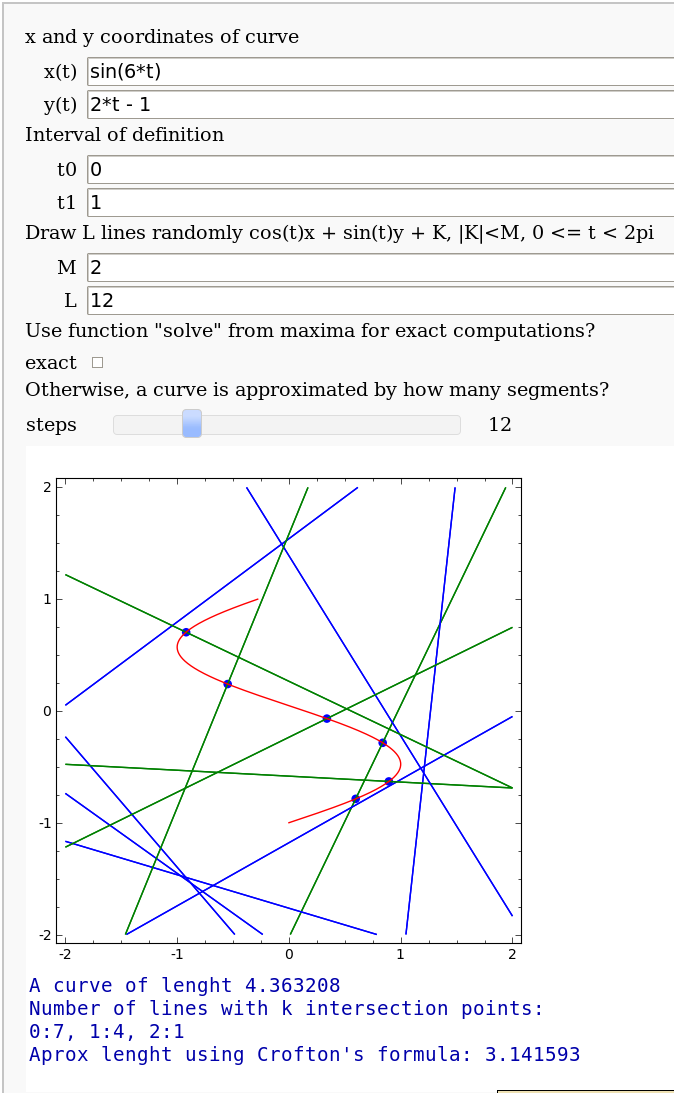
Crofton's formula
by Pablo Angulo. Illustrates Crofton's formula by throwing some random lines and computing the intersection number with a given curve. May use either solve for exact computation of the intersections, or may also approximate the curve by straight segments (this is the default).
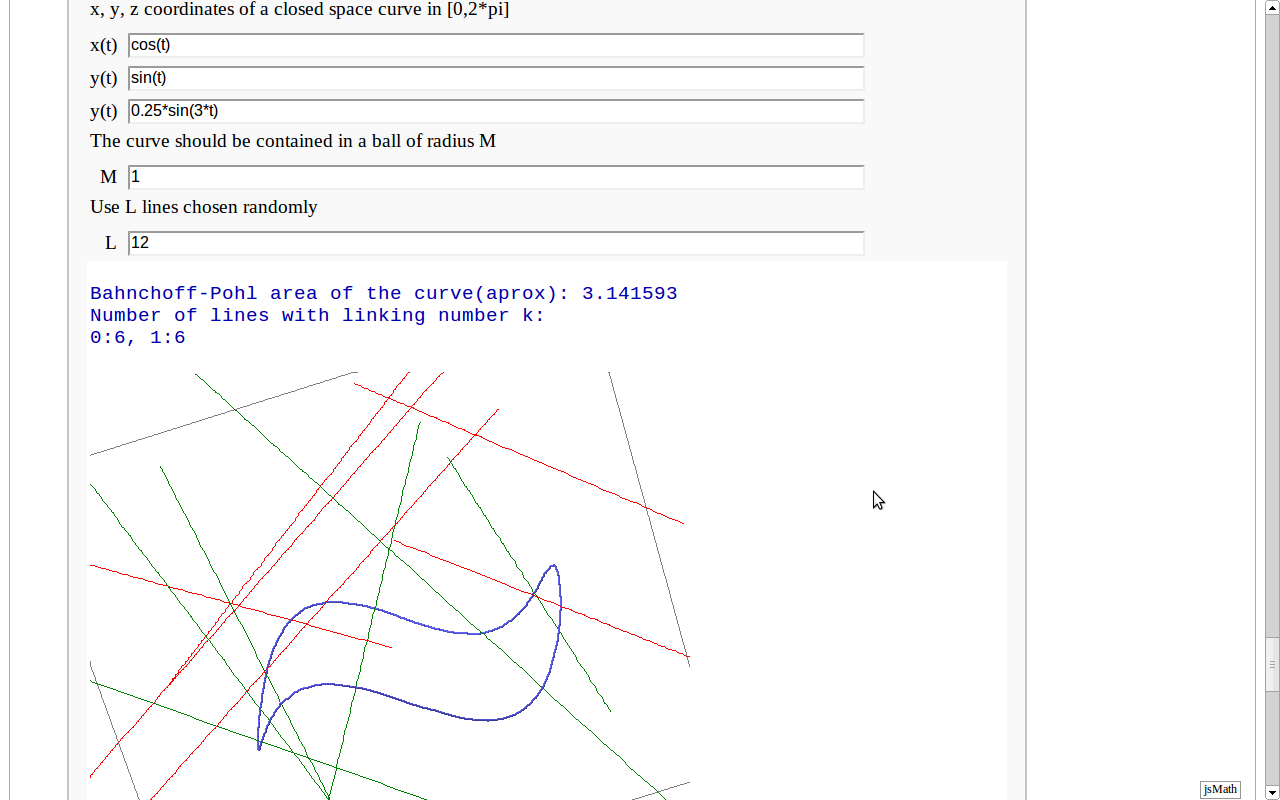
Banchoff-Pohl area
by Pablo Angulo. Computes the Banchoff-Pohl "area enclosed by a spatial curve", by throwing some random lines and computing the linking number with the given curve. Lines not linked to the given curve are displayed in red, linked lines are displayed in green.