|
Size: 20507
Comment:
|
Size: 18492
Comment: fixes geodesics interact
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 144: | Line 144: |
| # second interact | }}} Second interact: now we draw the geodesics {{{#!sagecell |
| Line 439: | Line 444: |
== Quantum tetrahedron volume eigenvalues == by David Horgan. Computes the volume eigenvalues of a quantum tetrahedron. {{{#!sagecell html('<h3>Quantum tetrahedron Volume Eigenvalue</h3>') html('Enter the four J values into the input boxes') html('k values k ranges from kmin to kmax in integer steps') html('The dimension d of the Hilbert space H4, d = kmax - kmin + 1') html('kmin = max(|j1-j2|,|j3 -j4|) kmax = min(j1+j2,j3 +j4)') html('The the dimension of the hilbert space is given by d = kmax -kmin + 1') html('V^2 =M = 2/9(real antisymmetrix matrix))') html('Spins must satisfy (j1+j2)<= (j3+j4)') html('Reference: Bohr-Sommerfeld Quantization of Space by Eugenio Bianchi and Hal M. Haggard ') import numpy @interact def _(j1 = input_box(6.0, 'J1'), j2= input_box(6.0, 'J2'), j3= input_box(6.0, 'J3'), j4= input_box(7.0, 'J1'), auto_update=False): if (j1+j2)<= (j3+j4): html('<h3>Values of Volume Eigenvalue</h3>') kmin = int(max(abs(j1-j2),abs(j3 -j4))) kmax = int(min((j1+j2),(j3 +j4))) d = kmax -kmin + 1 y=numpy.arange(kmin,kmax+1,1) kmatrix = matrix(CDF,int(d), int(d)) r=list() for j in range(d): k=int(y[j]) c1 = -i*k c2 = sqrt(4*k*k - 1) c3 = sqrt(j1*(j1+1)) c4 = sqrt((2*j1+1)) c5 = sqrt(j3*(j3+1)) c6 = sqrt((2*j3+1)) c7 = wigner_6j(j1,1,j1,k,j2,k-1) c8 = wigner_6j(j3,1,j3,k,j4,k-1) a = c1*c2*c3*c4*c5*c6*c7*c8 r.append(a) q=numerical_approx(a, digits=10) #print r for j in range(d-1): kmatrix[[j],[j+1]]=r[j+1] kmatrix[[j+1],[j]]=-r[j+1] #print kmatrix M = (2/9)*kmatrix #print M s=M.eigenvalues() #print s for j in range(d): e= sqrt(s[j]) if e.imag() ==0: print (e) }}} |
Sage Interactions - Geometry
goto interact main page
Contents
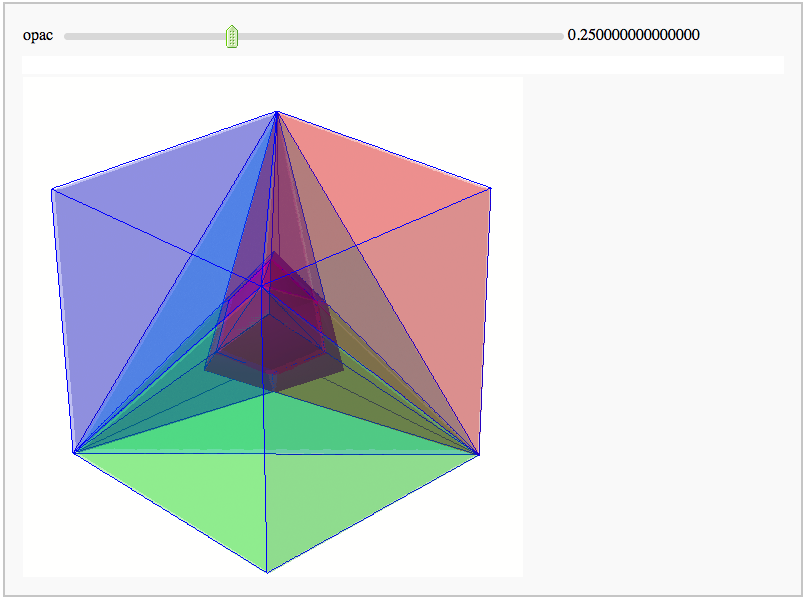
Intersecting tetrahedral reflections FIXME
by Marshall Hampton. Inspired by a question from Hans Schepker of Glass Geometry.
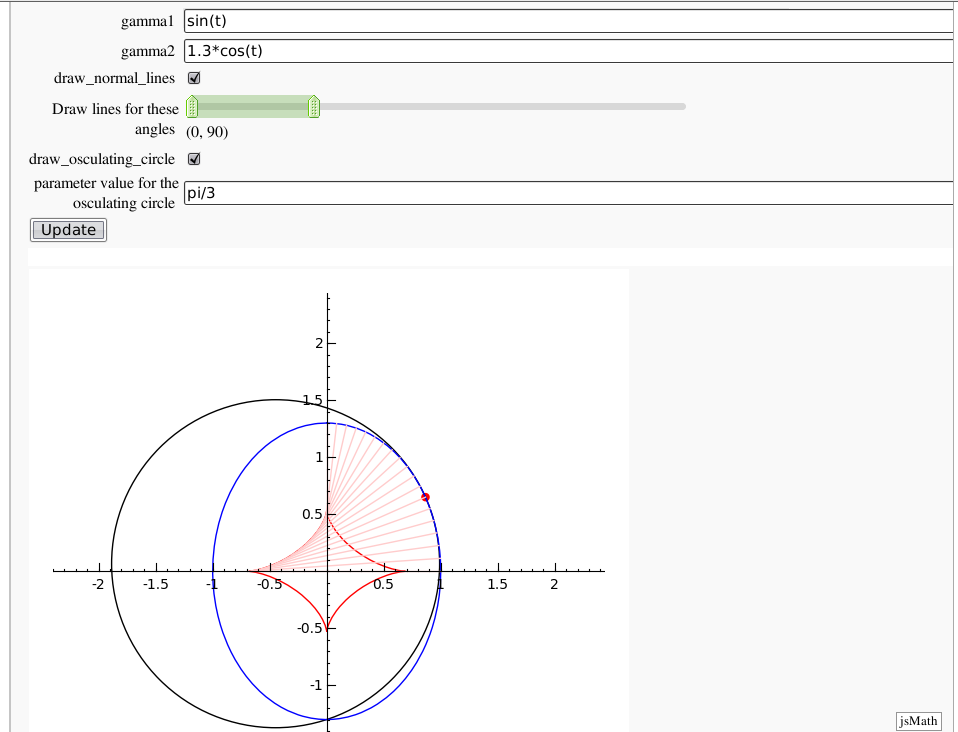
Evolutes
by Pablo Angulo. Computes the evolute of a plane curve given in parametric coordinates. The curve must be parametrized from the interval [0,2pi].
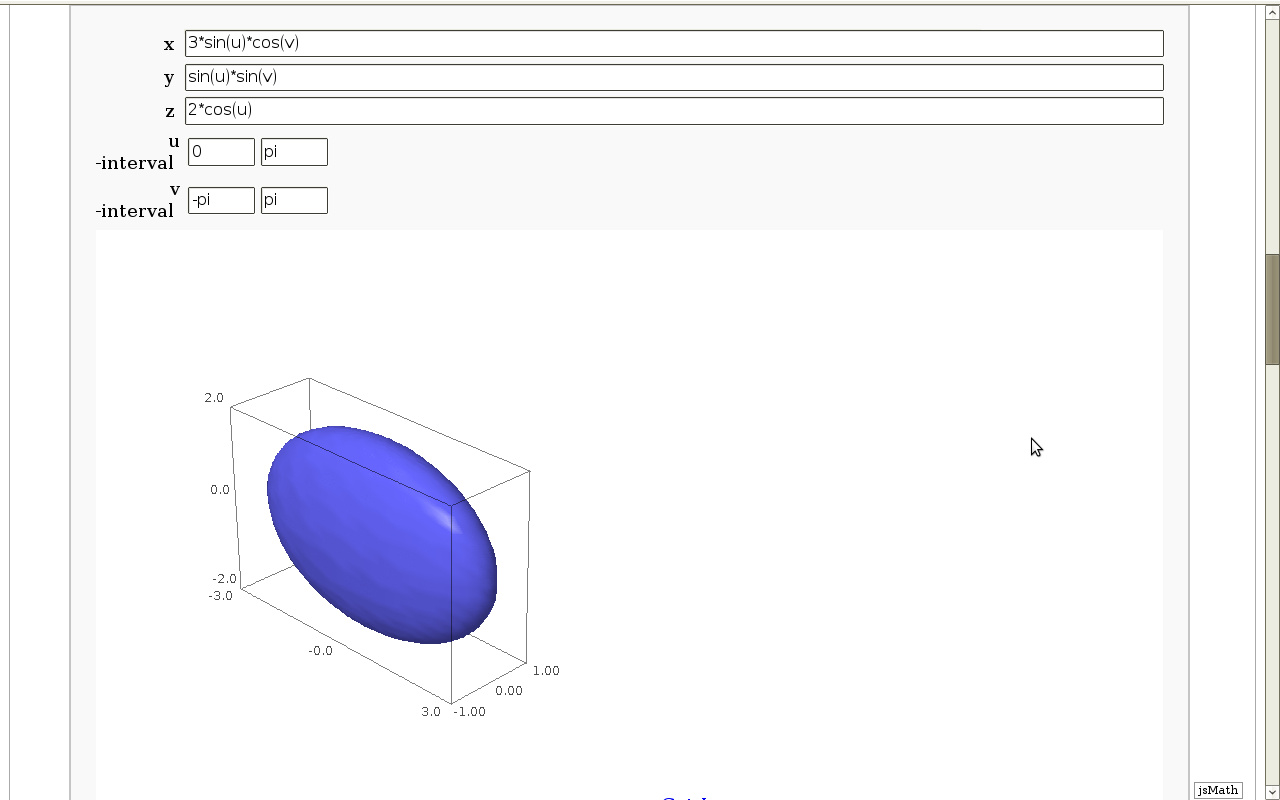
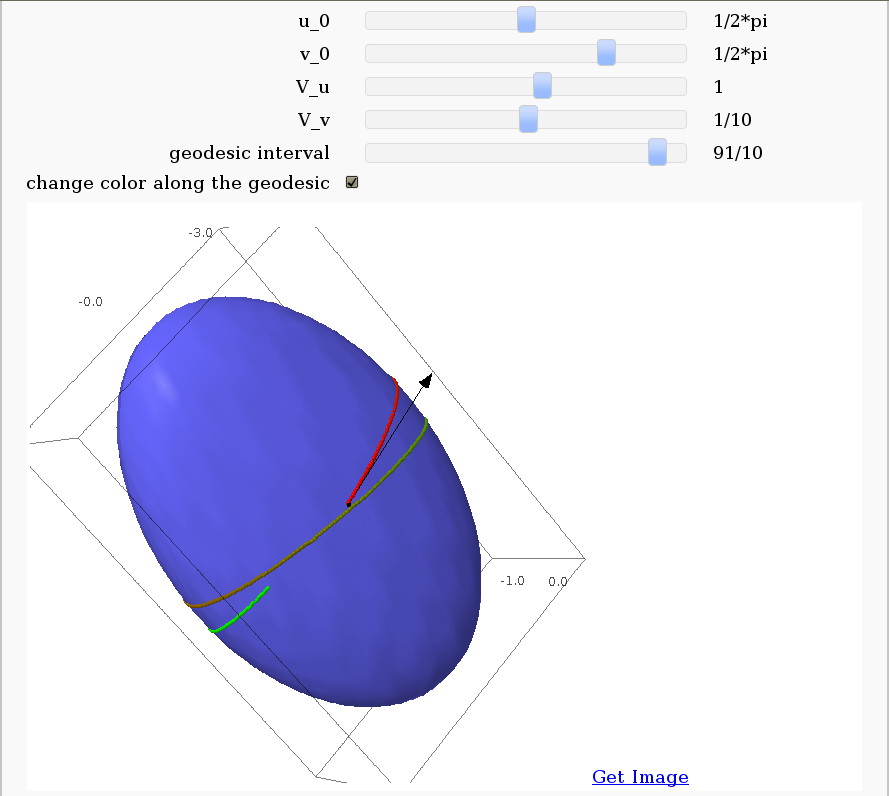
Geodesics on a parametric surface
by Antonio Valdés and Pablo Angulo. A first interact allows the user to introduce a parametric surface, and draws it. Then a second interact draws a geodesic within the surface. The separation is so that after the first interact, the geodesic equations are "compiled", and then the second interact is faster.
Second interact: now we draw the geodesics
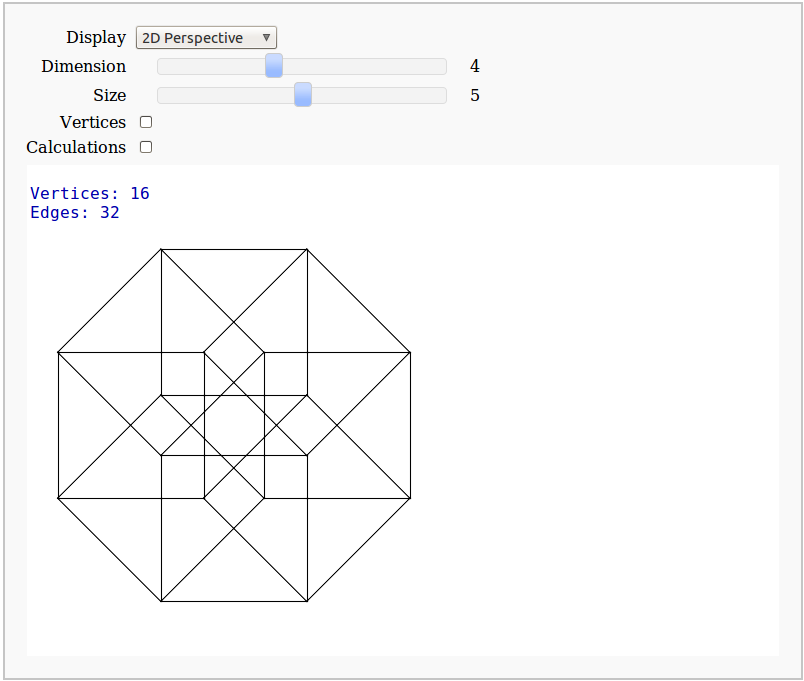
Dimensional Explorer
By Eviatar Bach
Renders 2D images (perspective or spring-layout) and 3D models of 0-10 dimensional hypercubes. It also displays number of edges and vertices.
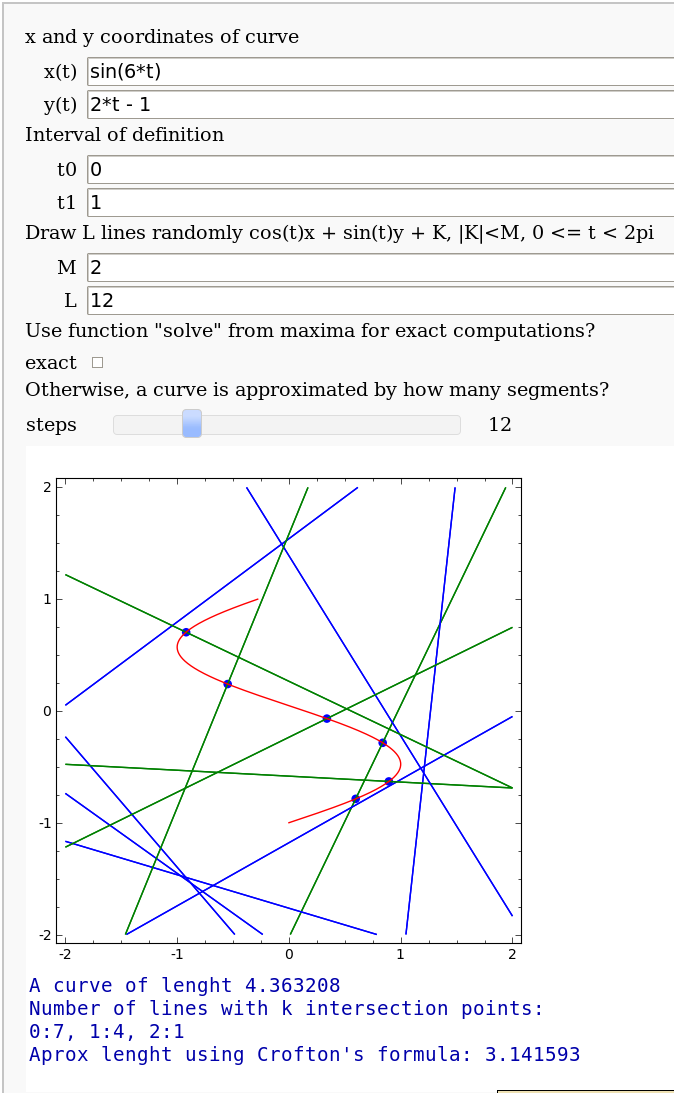
Crofton's formula
by Pablo Angulo. Illustrates Crofton's formula by throwing some random lines and computing the intersection number with a given curve. May use either solve for exact computation of the intersections, or may also approximate the curve by straight segments (this is the default).
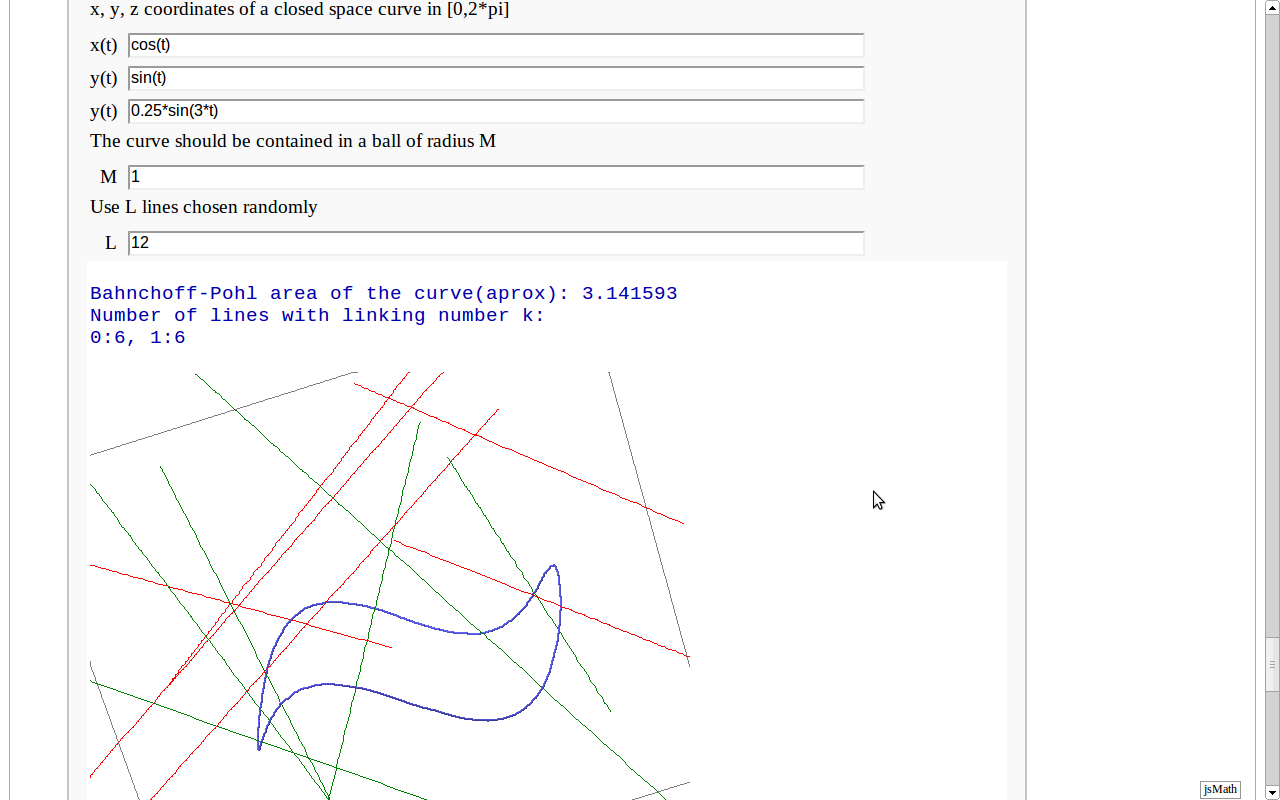
Banchoff-Pohl area
by Pablo Angulo. Computes the Banchoff-Pohl "area enclosed by a spatial curve", by throwing some random lines and computing the linking number with the given curve. Lines not linked to the given curve are displayed in red, linked lines are displayed in green.