|
Size: 15503
Comment: Added Crofton's formula
|
Size: 18327
Comment: fixing geodesics interact ...
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 6: | Line 6: |
| == Intersecting tetrahedral reflections == | == Intersecting tetrahedral reflections FIXME == |
| Line 8: | Line 8: |
| {{{ | {{{#!sagecell |
| Line 12: | Line 12: |
| p12 = p1.union(p2) | p12 = p1.convex_hull(p2) |
| Line 15: | Line 15: |
| p34 = p3.union(p4) | p34 = p3.convex_hull(p4) |
| Line 18: | Line 18: |
| p56 = p5.union(p6) | p56 = p5.convex_hull(p6) |
| Line 21: | Line 21: |
| p78 = p7.union(p8) | p78 = p7.convex_hull(p8) |
| Line 36: | Line 36: |
| {{{ | {{{#!sagecell |
| Line 52: | Line 52: |
| normal=(gammap[1]/norma(gammap), -gammap[0]/norma(gammap)) | np=norma(gammap) |
| Line 54: | Line 54: |
| np=norma(gammap) | |
| Line 57: | Line 55: |
| pe=gammap[0]*gammapp[0]+gammap[1]*gammapp[1] | normal=(gammap[1]/np, -gammap[0]/np) |
| Line 80: | Line 79: |
| show(grafica,aspect_ratio=1,xmin=-2,xmax=2,ymin=-2,ymax=2)}}} | show(grafica,aspect_ratio=1,xmin=-2,xmax=2,ymin=-2,ymax=2) }}} |
| Line 85: | Line 85: |
| by Antonio Valdés and Pablo Angulo. A first interact allows the user to introduce a parametric surface, and draws it. Then a second interact draws a geodesic within the surface. The separation is so that after the first interact, the geodesic equations are "compiled", and then the second interact is faster. {{{ u, v, t = var('u v t') |
by Antonio Valdés and Pablo Angulo. This example was originally composed of two interacts: - the first allowing the user to introduce a parametric surface, and draw it. - the second drawing a geodesic within the surface. The separation was so that after the first interact, the geodesic equations were "compiled", thus making the second interact faster. This still looks as a good idea to me, so please read the original code at https://malabares.cancamusa.net/home/pub/14/ But the following is fixed so that there is only one interact, and sagecell works. There might be another way yto {{{#!sagecell from scipy.integrate import odeint u, v, t, du, dv = var('u v t du dv') def fading_line3d(points, rgbcolor1, rgbcolor2, *args, **kwds): L = len(points) vcolor1 = vector(RDF, rgbcolor1) vcolor2 = vector(RDF, rgbcolor2) return sum(line3d(points[j:j+2], rgbcolor = tuple( ((L-j)/L)*vcolor1 + (j/L)*vcolor2 ), *args, **kwds) for j in srange(L-1)) steps = 100 |
| Line 92: | Line 113: |
| _int_u = input_grid(1, 2, default = [[0,pi]], label = 'u -interval'), _int_v = input_grid(1, 2, default = [[-pi,pi]], label = 'v -interval')): global F, Fu, Fv, func, S_plot, int_u, int_v int_u = _int_u[0] int_v = _int_v[0] |
int_u = input_grid(1, 2, default = [[0,pi]], label = 'u -interval'), int_v = input_grid(1, 2, default = [[-pi,pi]], label = 'v -interval'), init_point = input_grid(1, 2, default = [[-pi/4,pi/8]], label = 'coordinates of \ninitial point'), init_vector = input_grid(1, 2, default = [[1,0]], label = 'coordinates of \ninitial vector'), int_s = slider(0, 10, 1/10, default = pi/2, label = 'geodesic interval'), sliding_color = checkbox(True,'change color along the geodesic')): int_u = int_u[0] int_v = int_v[0] u_0, v_0 = init_point[0] V_u, V_v = init_vector[0] |
| Line 104: | Line 132: |
| S_plot.show(aspect_ratio = [1, 1, 1]) |
|
| Line 143: | Line 170: |
| Point = [u_0, v_0] velocity = [V_u, V_v] Point = map(float, Point) velocity = map(float, velocity) geo2D_aux = odeint(func, y0 = [velocity[0], velocity[1], Point[0], Point[1]], t = srange(0, int_s, 0.01)) geo3D = [F(u=l,v=r) for [j, k, l, r] in geo2D_aux] if sliding_color: g_plot = fading_line3d(geo3D, rgbcolor1 = (1, 0, 0), rgbcolor2 = (0, 1, 0), thickness=4) else: g_plot = line3d(geo3D, rgbcolor=(0, 1, 0), thickness=4) P = F(u=Point[0], v=Point[1]) P_plot = point3d((P[0], P[1], P[2]), rgbcolor = (0, 0, 0), pointsize = 30) V = velocity[0] * Fu(u = Point[0], v = Point[1]) + \ velocity[1] * Fv(u= Point[0], v = Point[1]) V_plot = arrow3d(P, P + V, color = 'black') show(g_plot + S_plot + V_plot + P_plot,aspect_ratio = [1, 1, 1]) |
|
| Line 146: | Line 196: |
| {{{ from scipy.integrate import odeint def fading_line3d(points, rgbcolor1, rgbcolor2, *args, **kwds): L = len(points) vcolor1 = vector(RDF, rgbcolor1) vcolor2 = vector(RDF, rgbcolor2) return sum(line3d(points[j:j+2], rgbcolor = tuple( ((L-j)/L)*vcolor1 + (j/L)*vcolor2 ), *args, **kwds) for j in srange(L-1)) steps = 100 @interact def _(u_0 = slider(int_u[0], int_u[1], (int_u[1] - int_u[0])/100, default = (int_u[0] + int_u[1])/2, label = 'u_0'), v_0 = slider(int_v[0], int_v[1], (int_v[1] - int_v[0])/100, default = (int_v[0] + int_v[1])/2, label = 'v_0'), V_u = slider(-10, 10, 1/10, default = 1, label = 'V_u'), V_v = slider(-10, 10, 1/10, default = 0, label = 'V_v'), int_s = slider(0, 10, 1/10, default = (int_u[1] - int_u[0])/2, label = 'geodesic interval'), sliding_color = checkbox(True,'change color along the geodesic')): du, dv, u, v = var('du dv u v') Point = [u_0, v_0] velocity = [V_u, V_v] Point = map(float, Point) velocity = map(float, velocity) geo2D_aux = odeint(func, y0 = [velocity[0], velocity[1], Point[0], Point[1]], t = srange(0, int_s, 0.01)) geo3D = [F(u=l,v=r) for [j, k, l, r] in geo2D_aux] if sliding_color: g_plot = fading_line3d(geo3D, rgbcolor1 = (1, 0, 0), rgbcolor2 = (0, 1, 0), thickness=4) else: g_plot = line3d(geo3D, rgbcolor=(0, 1, 0), thickness=4) P = F(u=Point[0], v=Point[1]) P_plot = point3d((P[0], P[1], P[2]), rgbcolor = (0, 0, 0), pointsize = 30) V = velocity[0] * Fu(u = Point[0], v = Point[1]) + \ velocity[1] * Fv(u= Point[0], v = Point[1]) V_plot = arrow3d(P, P + V, color = 'black') show(g_plot + S_plot + V_plot + P_plot,aspect_ratio = [1, 1, 1]) }}} |
|
| Line 203: | Line 202: |
| {{{ | {{{#!sagecell |
| Line 247: | Line 246: |
| {{{ | {{{#!sagecell |
| Line 334: | Line 333: |
| }}} {{{ |
|
| Line 358: | Line 355: |
| print 'Aprox lenght using Crofton\'s formula: %f'%((cortes_tot/L)*(pi*M)) | print 'Approx length using Crofton\'s formula: %f'%((cortes_tot/L)*(pi*M)) |
| Line 361: | Line 358: |
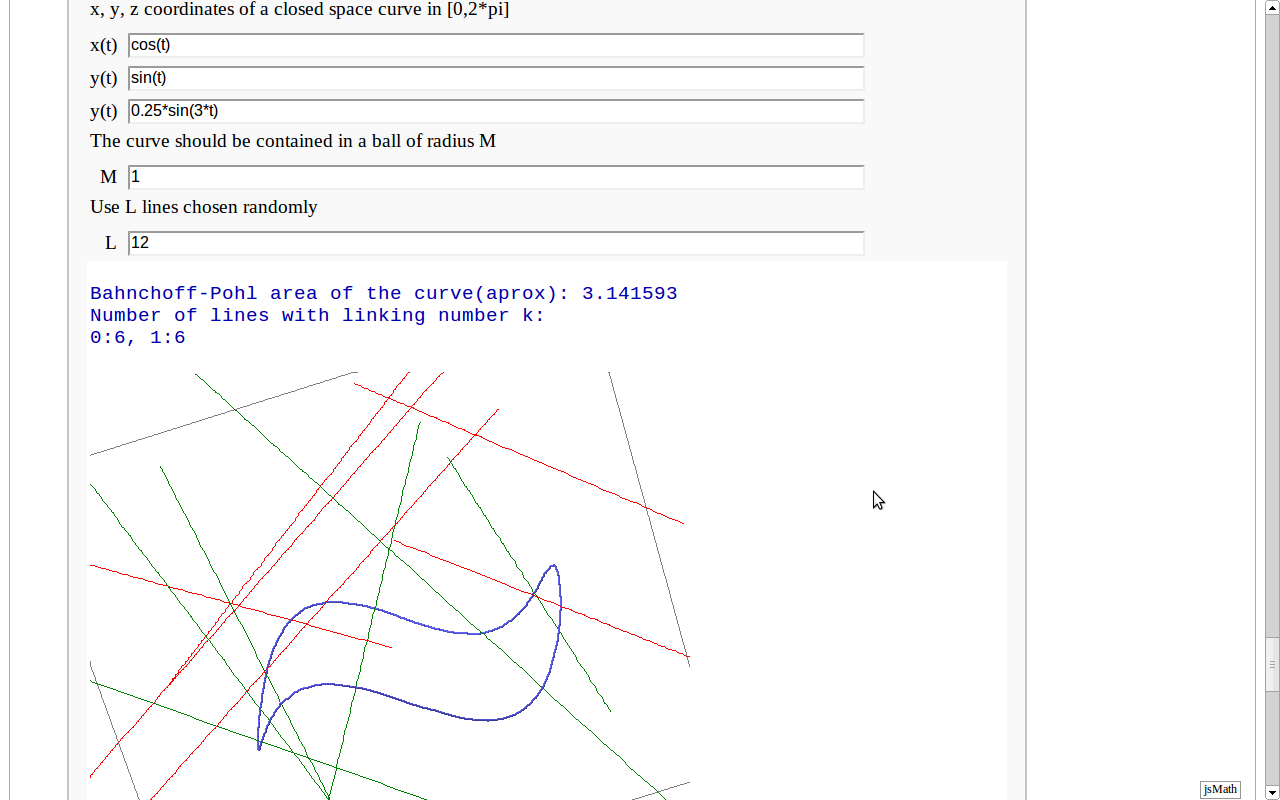
== Banchoff-Pohl area == by Pablo Angulo. Computes the Banchoff-Pohl "area enclosed by a spatial curve", by throwing some random lines and computing the linking number with the given curve. Lines not linked to the given curve are displayed in red, linked lines are displayed in green. {{{#!sagecell from collections import defaultdict var('t') a = 0; b= 2*pi def random_line3d(bound): '''Random line in R^3: first choose the guiding vector of the line, then choose a point in the plane p perpendicular to that vector. ''' p = vector([(2*random() - 1) for _ in range(3)]) v = p/norm(p) v2, v3 = matrix(v).right_kernel().basis() if det(matrix([v, v2, v3]))<0: v2, v3 = v3, v2 v2 = v2/norm(v2) v3 = v3 - (v3*v2)*v2 v3 = v3/norm(v3) return v, (2*random()*bound - bound, v2), (2*random()*bound - bound, v3) def winding_number(x, y, x0, y0): x -= x0 y -= y0 r2 = x^2 + y^2 xp = x.derivative(t) yp = y.derivative(t) integrando(t) = (x*yp -y*xp)/r2 i,e = numerical_integral(integrando, a, b) return round(i/(2*pi)) def linking_number(curve, line): v, (a2, v2), (a3, v3) = line M = matrix([v, v2, v3]) # curve2d = (curve*M.inverse())[1:] #This is VERY slow, for some reason! curve2d = sum(c*v for c,v in zip(curve,M.inverse()))[1:] x, y = curve2d return winding_number(x, y, a2,a3) def color_ln(number): if number: return (0,1-1/(1+number),0) else: return (1,0,0) def banchoff_pohl(curve, L, M): ln_d = defaultdict(int) pp = parametric_plot3d(curve, (t,0,2*pi), thickness=2) for k in range(L): a_line = random_line3d(M) ln = abs(linking_number(curve, a_line)) v, (l1, v1), (l2, v2) = a_line pp += parametric_plot3d(l1*v1+l2*v2+t*v,(t,-2,2), color=color_ln(ln)) ln_d[ln] += 1 return ln_d, pp def print_stats(d): print 'Number of lines with linking number k:' print ', '.join('%d:%d'%(k,v) for k,v in d.iteritems()) @interact def bp_interact( u1 = text_control('x, y, z coordinates of a closed space curve in [0,2*pi]'), curvax = input_box(cos(t), label='x(t)' ), curvay = input_box(sin(t), label='y(t)' ), curvaz = input_box(0, label='y(t)' ), u2 = text_control('The curve should be contained in a ball of radius M'), M = 1, u3 = text_control('Use L lines chosen randomly'), L = 10): ln_d, p = banchoff_pohl(vector((curvax, curvay, curvaz)), L, M) p.show(aspect_ratio=1, xmin=-2, xmax=2, ymin=-2,ymax=2) bp_area_aprox = (sum(k^2*v for k,v in ln_d.iteritems())/L)*2*pi*M^2 print 'Bahnchoff-Pohl area of the curve(aprox): %f'%bp_area_aprox print_stats(ln_d) }}} {{attachment:banchoff-pohl.png}} |
Sage Interactions - Geometry
goto interact main page
Contents
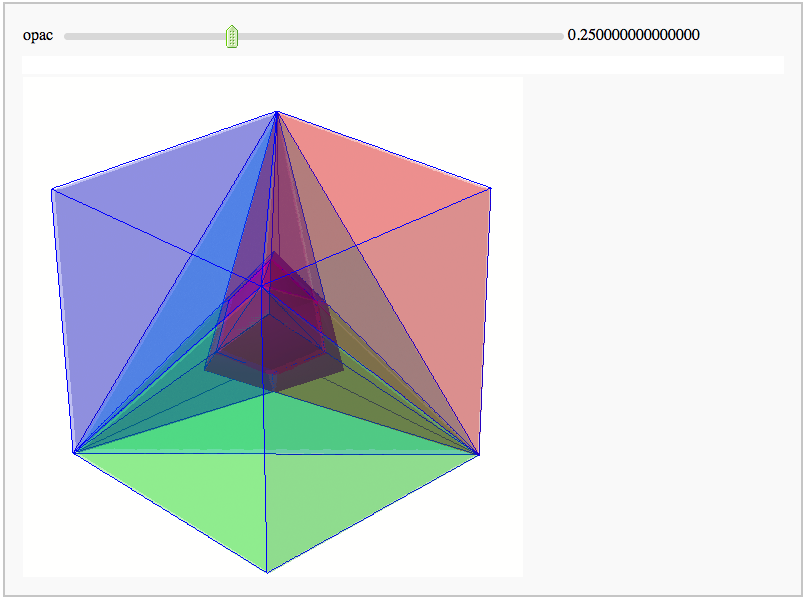
Intersecting tetrahedral reflections FIXME
by Marshall Hampton. Inspired by a question from Hans Schepker of Glass Geometry.
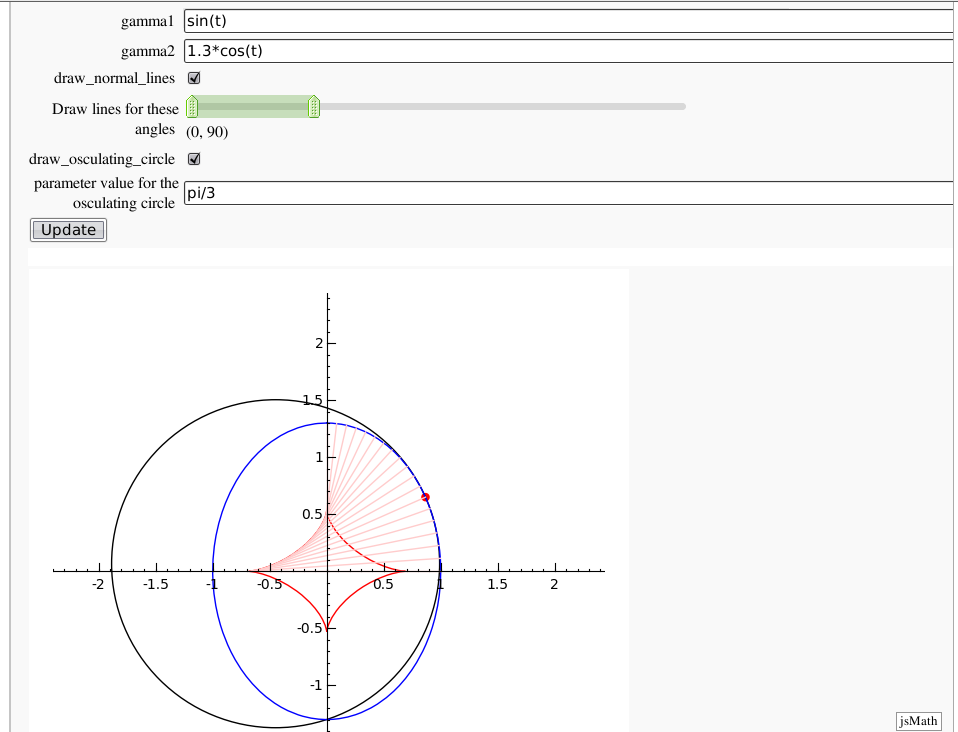
Evolutes
by Pablo Angulo. Computes the evolute of a plane curve given in parametric coordinates. The curve must be parametrized from the interval [0,2pi].
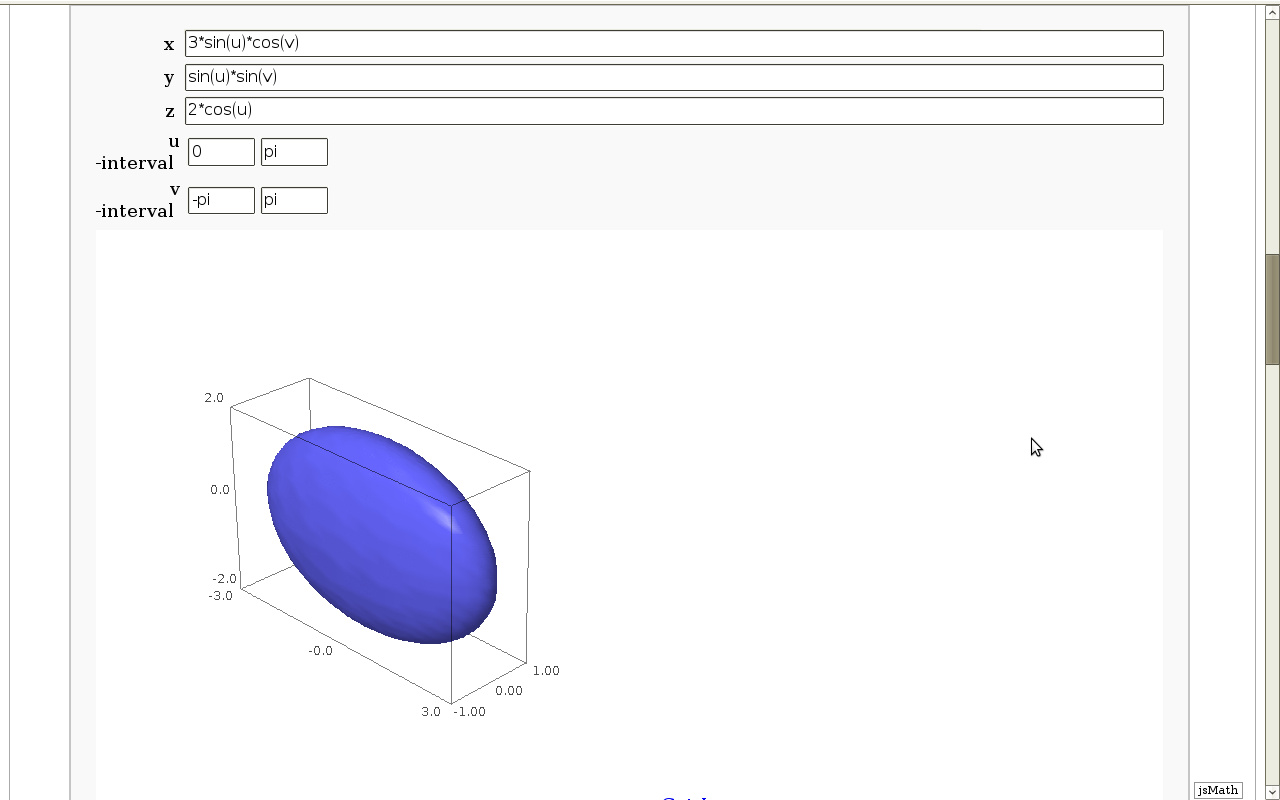
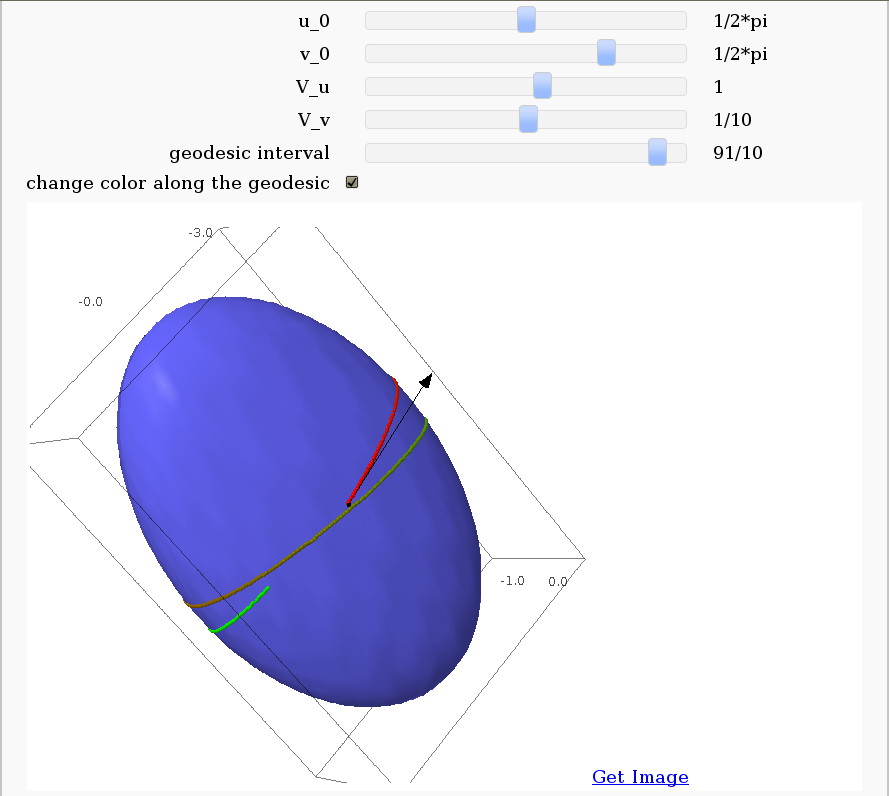
Geodesics on a parametric surface
by Antonio Valdés and Pablo Angulo. This example was originally composed of two interacts:
- - the first allowing the user to introduce a parametric surface, and draw it. - the second drawing a geodesic within the surface.
The separation was so that after the first interact, the geodesic equations were "compiled", thus making the second interact faster.
This still looks as a good idea to me, so please read the original code at https://malabares.cancamusa.net/home/pub/14/ But the following is fixed so that there is only one interact, and sagecell works. There might be another way yto
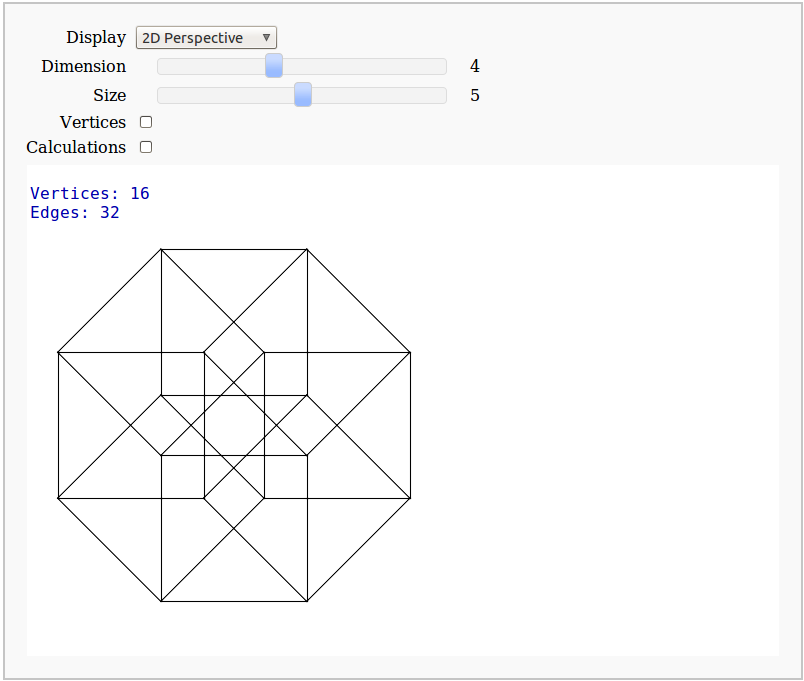
Dimensional Explorer
By Eviatar Bach
Renders 2D images (perspective or spring-layout) and 3D models of 0-10 dimensional hypercubes. It also displays number of edges and vertices.
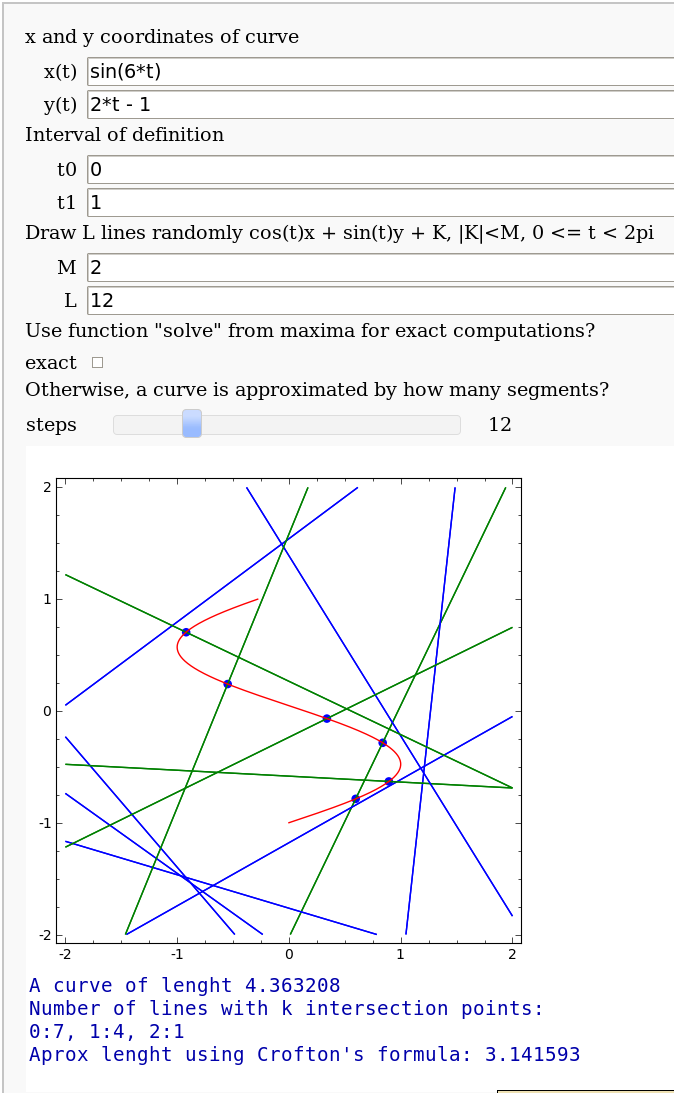
Crofton's formula
by Pablo Angulo. Illustrates Crofton's formula by throwing some random lines and computing the intersection number with a given curve. May use either solve for exact computation of the intersections, or may also approximate the curve by straight segments (this is the default).
Banchoff-Pohl area
by Pablo Angulo. Computes the Banchoff-Pohl "area enclosed by a spatial curve", by throwing some random lines and computing the linking number with the given curve. Lines not linked to the given curve are displayed in red, linked lines are displayed in green.