|
Size: 10955
Comment:
|
Size: 15503
Comment: Added Crofton's formula
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 243: | Line 243: |
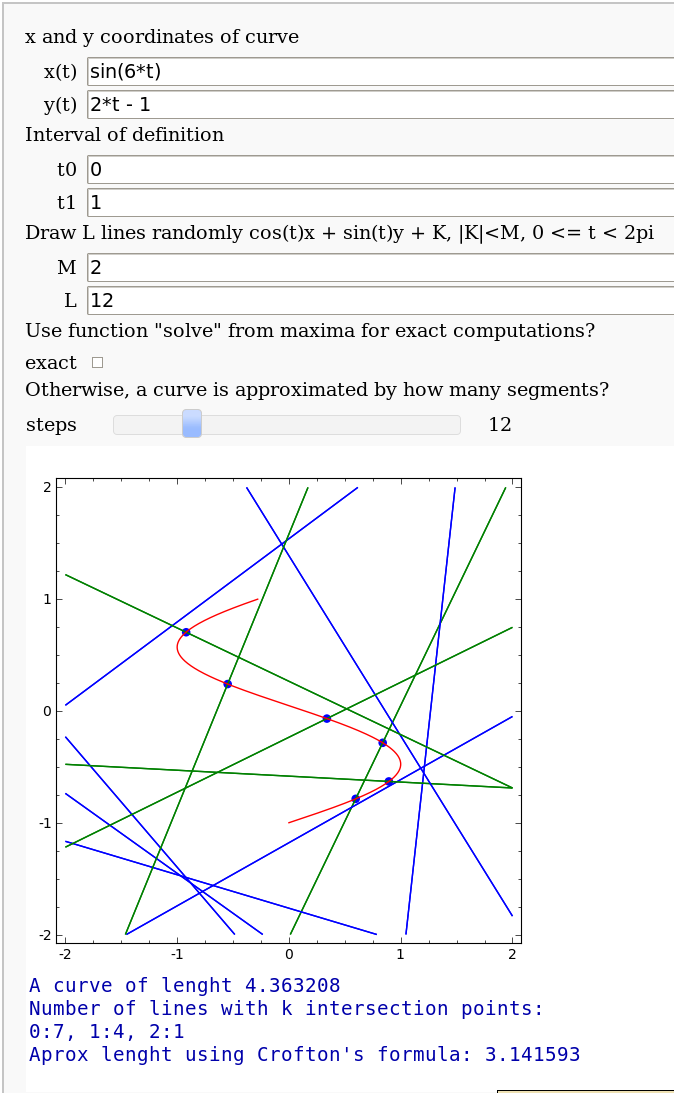
== Crofton's formula == by Pablo Angulo. Illustrates [[http://en.wikipedia.org/wiki/Crofton%27s_formula| Crofton's formula]] by throwing some random lines and computing the intersection number with a given curve. May use either solve for exact computation of the intersections, or may also approximate the curve by straight segments (this is the default). {{{ from collections import defaultdict var('t x y') pin = pi.n() def longitud(curva, t0, t1): dxdt = derivative(curva[0], t) dydt = derivative(curva[1], t) integrando(t) = sqrt(dxdt^2 + dydt^2) i,_ = numerical_integral(integrando, t0, t1) return i def random_line(cota): theta = random()*pin k = 2*cota*random() - cota return sin(theta)*x + cos(theta)*y + k def crofton_exact(curva, t0, t1, L, M): forget() assume(t>t0) assume(t<t1) pp = parametric_plot(curva, (t, t0, t1), color='red') cortesd = defaultdict(int) for k in range(L): rl = random_line(M) ss = solve(rl(x=curva[0], y=curva[1]), t) cortes = 0 for s in ss: tt = s.rhs() x0,y0 = curva[0](t=tt), curva[1](t=tt) if x0 in RR and y0 in RR: pp += point2d((x0,y0), pointsize = 30) cortes += 1 if cortes: pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='green') else: pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='blue') cortesd[cortes] += 1 return cortesd, pp def random_line_n(cota): theta = random()*pin k = 2*cota*random() - cota return sin(theta), cos(theta), k def interseccion_sr(punto1, punto2, recta): 'Devuelve el punto de interseccion de una recta y un segmento, o None si no se cortan' x1, y1 = punto1 x2, y2 = punto2 a, b, c = recta num = (-c - a*x1 - b*y1) den = (a*(x2 - x1) + b*(y2 - y1)) if (0 < num < den) or (den < num < 0): t_i = num/den return ((1-t_i)*x1 + t_i*x2, (1-t_i)*y1 + t_i*y2) else: return None def interseccion_cr(curva, t0, t1, recta, partes=50): '''Devuelve el numero de puntos de interseccion de una curva y una recta''' x,y = curva paso = (t1 - t0)/partes puntos = [(x(t=tr), y(t=tr)) for tr in srange(t0, t1 + paso, paso)] intersecciones = (interseccion_sr(puntos[j], puntos[j+1], recta) for j in xrange(partes-1)) return [p for p in intersecciones if p ] def crofton_aprox(curva, t0, t1, L, M): cortesd = defaultdict(int) pp = parametric_plot(curva, (t, t0, t1), color='red') for k in range(L): a,b,c = random_line_n(M) rl = a*x + b*y + c cortes = interseccion_cr(curva, t0, t1, (a,b,c)) if cortes: pp += sum(point2d(p, pointsize = 30) for p in cortes) pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='green') else: pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='blue') cortesd[len(cortes)] += 1 return cortesd, pp def print_stats(d): print 'Number of lines with k intersection points:' print ', '.join('%d:%d'%(k,v) for k,v in d.iteritems()) }}} {{{ @interact def crofton_interact(u1 = text_control('x and y coordinates of curve'), curvax = input_box(t^2, label='x(t)' ), curvay = input_box(2*t-1, label='y(t)' ), u2 = text_control('Interval of definition'), t0 = 0, t1 = 1, u3 = text_control('Draw L lines randomly cos(t)x + sin(t)y + K, |K|<M, 0 <= t < 2pi'), M = 2, L = 5, u4 = text_control('Use function "solve" from maxima for exact computations?'), exact = checkbox(False), u5 = text_control('Otherwise, a curve is approximated by how many segments?'), steps = slider(4, 40, 4, 8)): if exact: cortesd, p = crofton_exact((curvax, curvay), t0, t1, L, M) else: cortesd, p = crofton_aprox((curvax, curvay), t0, t1, L, M) p.show(aspect_ratio=1, xmin=-2, xmax=2, ymin=-2,ymax=2) print 'A curve of lenght %f'%longitud((curvax, curvay), t0, t1) print_stats(cortesd) cortes_tot = sum(k*v for k,v in cortesd.iteritems()) print 'Aprox lenght using Crofton\'s formula: %f'%((cortes_tot/L)*(pi*M)) }}} {{attachment:crofton4.png}} |
Sage Interactions - Geometry
goto interact main page
Contents
Intersecting tetrahedral reflections
by Marshall Hampton. Inspired by a question from Hans Schepker of Glass Geometry.
#Pairs of tetrahedra, one the reflection of the other in the internal face, are joined by union operations:
p1 = Polyhedron(vertices = [[1,1,1],[1,1,0],[0,1,1],[1,0,1]])
p2 = Polyhedron(vertices = [[1/3,1/3,1/3],[1,1,0],[0,1,1],[1,0,1]])
p12 = p1.union(p2)
p3 = Polyhedron(vertices = [[0,0,1],[0,0,0],[0,1,1],[1,0,1]])
p4 = Polyhedron(vertices = [[2/3,2/3,1/3],[0,0,0],[0,1,1],[1,0,1]])
p34 = p3.union(p4)
p5 = Polyhedron(vertices = [[1,0,0],[1,0,1],[0,0,0],[1,1,0]])
p6 = Polyhedron(vertices = [[1/3,2/3,2/3],[1,0,1],[0,0,0],[1,1,0]])
p56 = p5.union(p6)
p7 = Polyhedron(vertices = [[0,1,0],[0,0,0],[1,1,0],[0,1,1]])
p8 = Polyhedron(vertices = [[2/3,1/3,2/3],[0,0,0],[1,1,0],[0,1,1]])
p78 = p7.union(p8)
pti = p12.intersection(p34).intersection(p56).intersection(p78)
@interact
def tetra_plot(opac = slider(srange(0,1.0,.25), default = .25)):
p12r = p12.render_wireframe()+p12.render_solid(opacity = opac)
p34r = p34.render_wireframe()+p34.render_solid(rgbcolor = (0,0,1),opacity = opac)
p56r = p56.render_wireframe()+p56.render_solid(rgbcolor = (0,1,0),opacity = opac)
p78r = p78.render_wireframe()+p78.render_solid(rgbcolor = (0,1,1),opacity = opac)
ptir = pti.render_wireframe()+pti.render_solid(rgbcolor = (1,0,1),opacity = .9)
show(p12r+p34r+p56r+p78r+ptir, frame = False)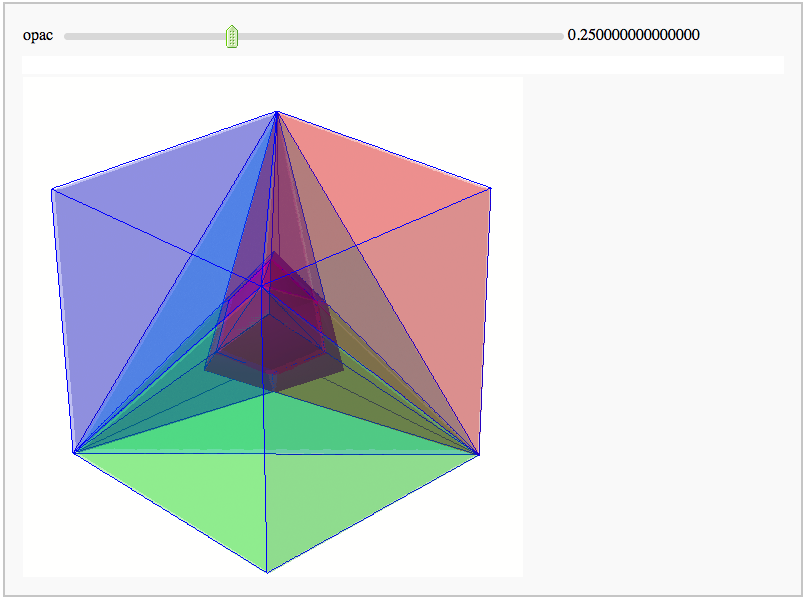
Evolutes
by Pablo Angulo. Computes the evolute of a plane curve given in parametric coordinates. The curve must be parametrized from the interval [0,2pi].
var('t');
def norma(v):
return sqrt(sum(x^2 for x in v))
paso_angulo=5
@interact
def _( gamma1=input_box(default=sin(t)), gamma2=input_box(default=1.3*cos(t)),
draw_normal_lines=True,
rango_angulos=range_slider(0,360,paso_angulo,(0,90),label='Draw lines for these angles'),
draw_osculating_circle=True,
t0=input_box(default=pi/3,label='parameter value for the osculating circle'),
auto_update=False ):
gamma=(gamma1,gamma2)
gammap=(gamma[0].derivative(),gamma[1].derivative())
normal=(gammap[1]/norma(gammap), -gammap[0]/norma(gammap))
gammapp=(gammap[0].derivative(),gammap[1].derivative())
np=norma(gammap)
npp=norma(gammapp)
pe=gammap[0]*gammapp[0]+gammap[1]*gammapp[1]
curvatura=(gammap[1]*gammapp[0]-gammap[0]*gammapp[1])/norma(gammap)^3
radio=1/curvatura
centros=(gamma[0]+radio*normal[0],gamma[1]+radio*normal[1])
curva=parametric_plot(gamma,(t,0,2*pi))
evoluta=parametric_plot(centros,(t,0,2*pi), color='red')
grafica=curva+evoluta
if draw_normal_lines:
f=2*pi/360
lineas=sum(line2d( [ (gamma[0](t=i*f), gamma[1](t=i*f)),
(centros[0](t=i*f), centros[1](t=i*f)) ],
thickness=1,rgbcolor=(1,0.8,0.8))
for i in range(rango_angulos[0], rango_angulos[1]+paso_angulo, paso_angulo))
grafica+=lineas
if draw_osculating_circle and 0<t0<2*pi:
punto=point((gamma[0](t=t0), gamma[1](t=t0)), rgbcolor=hue(0),pointsize=30)
circulo=circle( (centros[0](t=t0), centros[1](t=t0)), radio(t=t0) )
grafica+=punto+circulo
show(grafica,aspect_ratio=1,xmin=-2,xmax=2,ymin=-2,ymax=2)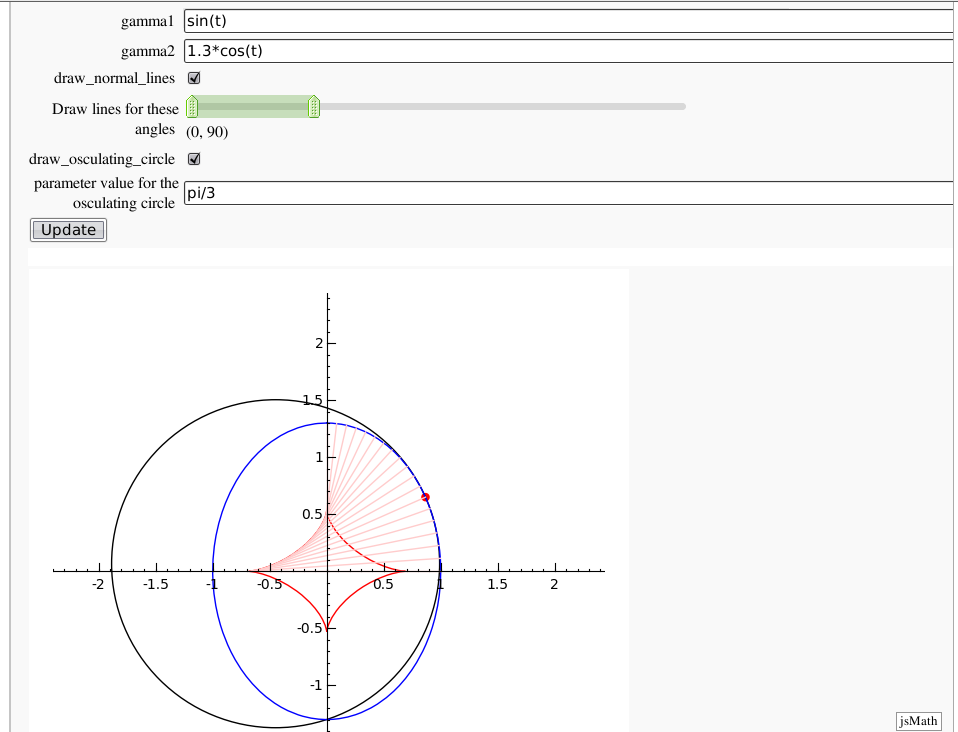
Geodesics on a parametric surface
by Antonio Valdés and Pablo Angulo. A first interact allows the user to introduce a parametric surface, and draws it. Then a second interact draws a geodesic within the surface. The separation is so that after the first interact, the geodesic equations are "compiled", and then the second interact is faster.
u, v, t = var('u v t')
@interact
def _(x = input_box(3*sin(u)*cos(v), 'x'),
y = input_box(sin(u)*sin(v), 'y'),
z = input_box(2*cos(u), 'z'),
_int_u = input_grid(1, 2, default = [[0,pi]], label = 'u -interval'),
_int_v = input_grid(1, 2, default = [[-pi,pi]], label = 'v -interval')):
global F, Fu, Fv, func, S_plot, int_u, int_v
int_u = _int_u[0]
int_v = _int_v[0]
F = vector([x, y, z])
S_plot = parametric_plot3d( F,
(u, int_u[0], int_u[1]),
(v, int_v[0], int_v[1]))
S_plot.show(aspect_ratio = [1, 1, 1])
dFu = F.diff(u)
dFv = F.diff(v)
Fu = fast_float(dFu, u, v)
Fv = fast_float(dFv, u, v)
ufunc = function('ufunc', t)
vfunc = function('vfunc', t)
dFtt = F(u=ufunc, v=vfunc).diff(t, t)
ec1 = dFtt.dot_product(dFu(u=ufunc, v=vfunc))
ec2 = dFtt.dot_product(dFv(u=ufunc, v=vfunc))
dv, ddv, du, ddu = var('dv, ddv, du, ddu')
diffec1 = ec1.subs_expr(diff(ufunc, t) == du,
diff(ufunc, t, t) == ddu,
diff(vfunc, t) == dv,
diff(vfunc, t, t) == ddv,
ufunc == u, vfunc == v)
diffec2 = ec2.subs_expr(diff(ufunc, t) == du,
diff(ufunc, t, t) == ddu,
diff(vfunc, t) == dv,
diff(vfunc, t, t) == ddv,
ufunc == u, vfunc == v)
sols = solve([diffec1 == 0 , diffec2 == 0], ddu, ddv)
ddu_rhs = (sols[0][0]).rhs().full_simplify()
ddv_rhs = (sols[0][1]).rhs().full_simplify()
ddu_ff = fast_float(ddu_rhs, du, dv, u, v)
ddv_ff = fast_float(ddv_rhs, du, dv, u, v)
def func(y,t):
v = list(y)
return [ddu_ff(*v), ddv_ff(*v), v[0], v[1]]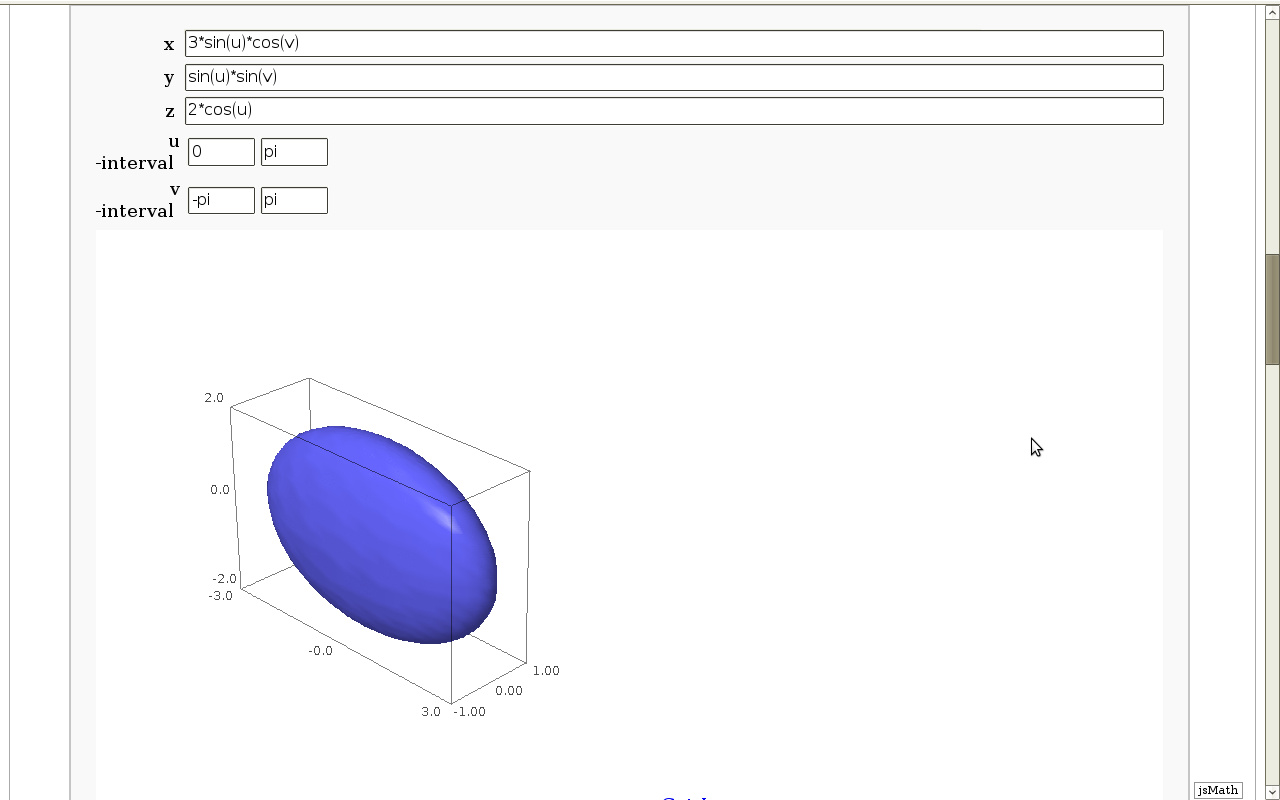
from scipy.integrate import odeint
def fading_line3d(points, rgbcolor1, rgbcolor2, *args, **kwds):
L = len(points)
vcolor1 = vector(RDF, rgbcolor1)
vcolor2 = vector(RDF, rgbcolor2)
return sum(line3d(points[j:j+2],
rgbcolor = tuple( ((L-j)/L)*vcolor1 + (j/L)*vcolor2 ),
*args, **kwds)
for j in srange(L-1))
steps = 100
@interact
def _(u_0 = slider(int_u[0], int_u[1], (int_u[1] - int_u[0])/100,
default = (int_u[0] + int_u[1])/2, label = 'u_0'),
v_0 = slider(int_v[0], int_v[1], (int_v[1] - int_v[0])/100,
default = (int_v[0] + int_v[1])/2, label = 'v_0'),
V_u = slider(-10, 10, 1/10, default = 1, label = 'V_u'),
V_v = slider(-10, 10, 1/10, default = 0, label = 'V_v'),
int_s = slider(0, 10, 1/10,
default = (int_u[1] - int_u[0])/2,
label = 'geodesic interval'),
sliding_color = checkbox(True,'change color along the geodesic')):
du, dv, u, v = var('du dv u v')
Point = [u_0, v_0]
velocity = [V_u, V_v]
Point = map(float, Point)
velocity = map(float, velocity)
geo2D_aux = odeint(func,
y0 = [velocity[0], velocity[1], Point[0], Point[1]],
t = srange(0, int_s, 0.01))
geo3D = [F(u=l,v=r) for [j, k, l, r] in geo2D_aux]
if sliding_color:
g_plot = fading_line3d(geo3D, rgbcolor1 = (1, 0, 0), rgbcolor2 = (0, 1, 0), thickness=4)
else:
g_plot = line3d(geo3D, rgbcolor=(0, 1, 0), thickness=4)
P = F(u=Point[0], v=Point[1])
P_plot = point3d((P[0], P[1], P[2]), rgbcolor = (0, 0, 0), pointsize = 30)
V = velocity[0] * Fu(u = Point[0], v = Point[1]) + \
velocity[1] * Fv(u= Point[0], v = Point[1])
V_plot = arrow3d(P, P + V, color = 'black')
show(g_plot + S_plot + V_plot + P_plot,aspect_ratio = [1, 1, 1])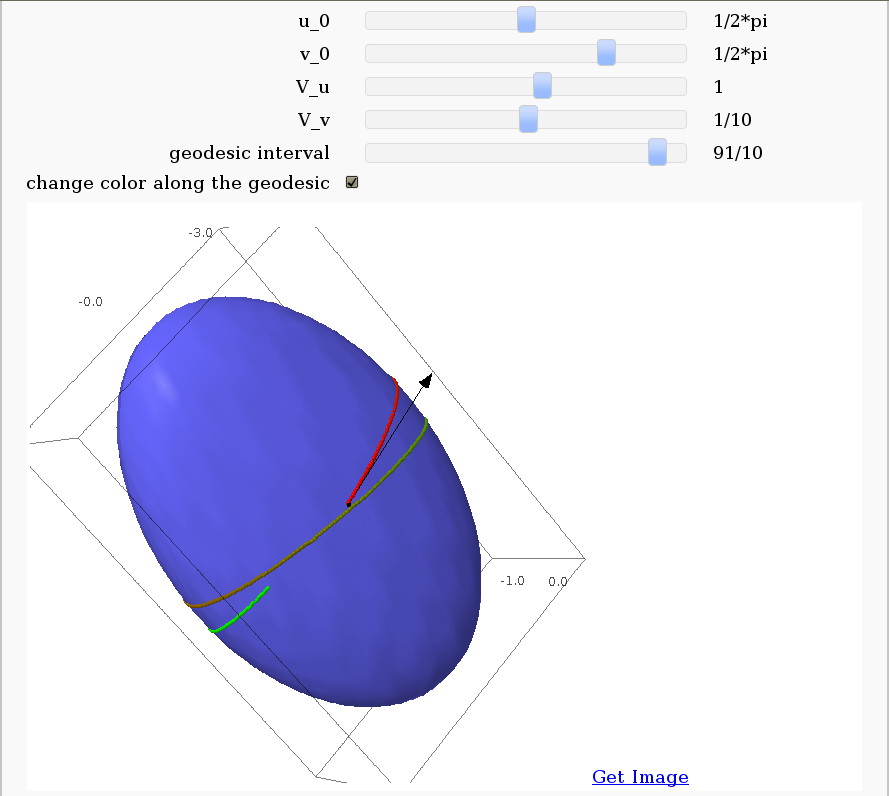
Dimensional Explorer
By Eviatar Bach
Renders 2D images (perspective or spring-layout) and 3D models of 0-10 dimensional hypercubes. It also displays number of edges and vertices.
@interact
def render(Display=selector(['2D Perspective', '2D Spring-layout', '3D']), Dimension=slider(0,10,default=4, step_size=1), Size=slider(0,10,default=5,step_size=1), Vertices=False, Calculations=False):
if Display=='2D Perspective':
if Dimension==0:
g=graphs.GridGraph([1])
print 'Vertices:', len(g.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(g.edges()), ('(%s*(%s/2))' %(len(g.vertices()), Dimension) if Calculations else '')
g.show(figsize=[Size,Size], vertex_size=30, vertex_labels=False, transparent=True, vertex_colors='black')
else:
g=graphs.CubeGraph(Dimension)
print 'Vertices:', len(g.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(g.edges()), ('(%s*(%s/2))' %(len(g.vertices()), Dimension) if Calculations else '')
g.show(figsize=[Size,Size], vertex_size=(20 if Vertices else 0), vertex_labels=False, transparent=True, vertex_colors='black')
if Display=='2D Spring-layout':
if Dimension==0:
s=graphs.GridGraph([1])
print 'Vertices:', len(s.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(s.edges()), ('(%s*(%s/2))' %(len(s.vertices()), Dimension) if Calculations else '')
s.show(figsize=[Size,Size], vertex_size=30, vertex_labels=False, transparent=True, vertex_colors='black')
else:
s=graphs.GridGraph([2]*Dimension)
print 'Vertices:', len(s.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(s.edges()), ('(%s*(%s/2))' %(len(s.vertices()), Dimension) if Calculations else '')
s.show(figsize=[Size,Size], vertex_size=(20 if Vertices else 0), vertex_labels=False, transparent=True, vertex_colors='black')
if Display=='3D':
if Dimension==0:
d=graphs.GridGraph([1])
print 'Vertices:', len(d.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(d.edges()), ('(%s*(%s/2))' %(len(d.vertices()), Dimension) if Calculations else '')
d.show3d(figsize=[Size/2,Size/2], vertex_size=0.001)
else:
d=graphs.CubeGraph(Dimension)
print 'Vertices:', len(d.vertices()), ('(2^%s)'%Dimension if Calculations else ''), '\nEdges:', len(d.edges()), ('(%s*(%s/2))' %(len(d.vertices()), Dimension) if Calculations else '')
d.show3d(figsize=[Size,Size], vertex_size=(0.03 if Vertices else 0.001))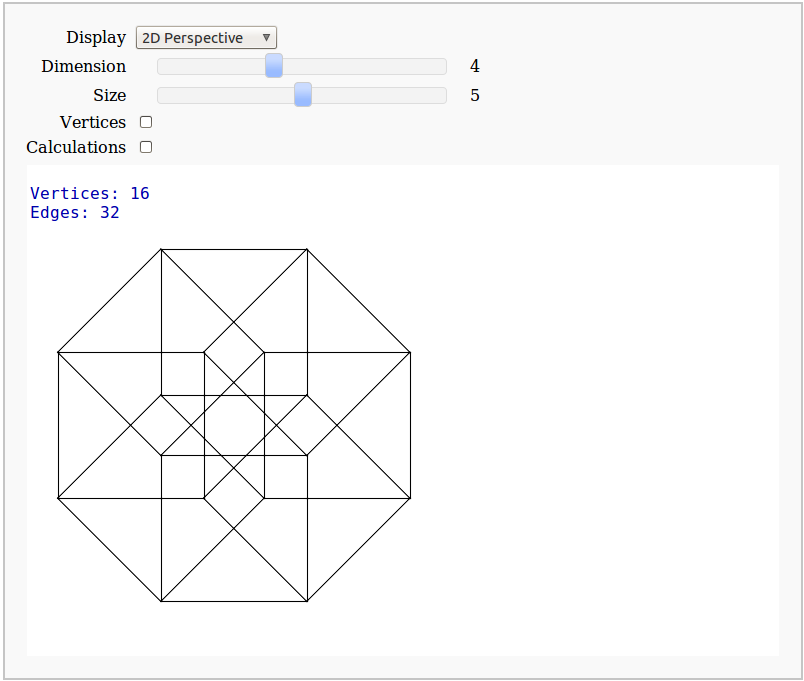
Crofton's formula
by Pablo Angulo. Illustrates Crofton's formula by throwing some random lines and computing the intersection number with a given curve. May use either solve for exact computation of the intersections, or may also approximate the curve by straight segments (this is the default).
from collections import defaultdict
var('t x y')
pin = pi.n()
def longitud(curva, t0, t1):
dxdt = derivative(curva[0], t)
dydt = derivative(curva[1], t)
integrando(t) = sqrt(dxdt^2 + dydt^2)
i,_ = numerical_integral(integrando, t0, t1)
return i
def random_line(cota):
theta = random()*pin
k = 2*cota*random() - cota
return sin(theta)*x + cos(theta)*y + k
def crofton_exact(curva, t0, t1, L, M):
forget()
assume(t>t0)
assume(t<t1)
pp = parametric_plot(curva, (t, t0, t1), color='red')
cortesd = defaultdict(int)
for k in range(L):
rl = random_line(M)
ss = solve(rl(x=curva[0], y=curva[1]), t)
cortes = 0
for s in ss:
tt = s.rhs()
x0,y0 = curva[0](t=tt), curva[1](t=tt)
if x0 in RR and y0 in RR:
pp += point2d((x0,y0), pointsize = 30)
cortes += 1
if cortes:
pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='green')
else:
pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='blue')
cortesd[cortes] += 1
return cortesd, pp
def random_line_n(cota):
theta = random()*pin
k = 2*cota*random() - cota
return sin(theta), cos(theta), k
def interseccion_sr(punto1, punto2, recta):
'Devuelve el punto de interseccion de una recta y un segmento, o None si no se cortan'
x1, y1 = punto1
x2, y2 = punto2
a, b, c = recta
num = (-c - a*x1 - b*y1)
den = (a*(x2 - x1) + b*(y2 - y1))
if (0 < num < den) or (den < num < 0):
t_i = num/den
return ((1-t_i)*x1 + t_i*x2, (1-t_i)*y1 + t_i*y2)
else:
return None
def interseccion_cr(curva, t0, t1, recta, partes=50):
'''Devuelve el numero de puntos de interseccion de una curva y una recta'''
x,y = curva
paso = (t1 - t0)/partes
puntos = [(x(t=tr), y(t=tr)) for tr in srange(t0, t1 + paso, paso)]
intersecciones = (interseccion_sr(puntos[j], puntos[j+1], recta)
for j in xrange(partes-1))
return [p for p in intersecciones if p ]
def crofton_aprox(curva, t0, t1, L, M):
cortesd = defaultdict(int)
pp = parametric_plot(curva, (t, t0, t1), color='red')
for k in range(L):
a,b,c = random_line_n(M)
rl = a*x + b*y + c
cortes = interseccion_cr(curva, t0, t1, (a,b,c))
if cortes:
pp += sum(point2d(p, pointsize = 30) for p in cortes)
pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='green')
else:
pp += implicit_plot(rl, (x,-M,M), (y,-M,M), color='blue')
cortesd[len(cortes)] += 1
return cortesd, pp
def print_stats(d):
print 'Number of lines with k intersection points:'
print ', '.join('%d:%d'%(k,v) for k,v in d.iteritems())@interact
def crofton_interact(u1 = text_control('x and y coordinates of curve'),
curvax = input_box(t^2, label='x(t)' ),
curvay = input_box(2*t-1, label='y(t)' ),
u2 = text_control('Interval of definition'),
t0 = 0, t1 = 1,
u3 = text_control('Draw L lines randomly cos(t)x + sin(t)y + K, |K|<M, 0 <= t < 2pi'),
M = 2,
L = 5,
u4 = text_control('Use function "solve" from maxima for exact computations?'),
exact = checkbox(False),
u5 = text_control('Otherwise, a curve is approximated by how many segments?'),
steps = slider(4, 40, 4, 8)):
if exact:
cortesd, p = crofton_exact((curvax, curvay), t0, t1, L, M)
else:
cortesd, p = crofton_aprox((curvax, curvay), t0, t1, L, M)
p.show(aspect_ratio=1, xmin=-2, xmax=2, ymin=-2,ymax=2)
print 'A curve of lenght %f'%longitud((curvax, curvay), t0, t1)
print_stats(cortesd)
cortes_tot = sum(k*v for k,v in cortesd.iteritems())
print 'Aprox lenght using Crofton\'s formula: %f'%((cortes_tot/L)*(pi*M))