|
Size: 15336
Comment:
|
Size: 19017
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 8: | Line 8: |
| {{{ | {{{#!sagecell |
| Line 30: | Line 30: |
| steps_shown = max(nsteps,show_steps) | steps_shown = min(nsteps,show_steps) |
| Line 49: | Line 49: |
| {{{ | {{{#!sagecell |
| Line 83: | Line 83: |
| {{{ | {{{#!sagecell |
| Line 130: | Line 130: |
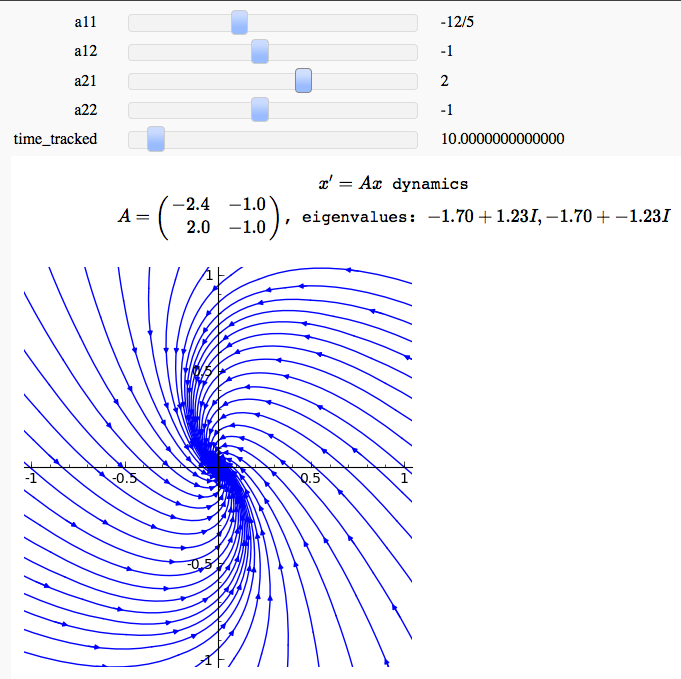
| == Linear two-dimensional ODEs == by Marshall Hampton {{{#!sagecell %cython cpdef c_euler_m(double t0, double x10, double x20, double tend, int steps, double a11, double a12, double a21, double a22, double cutoff = 10): cdef double h = (tend-t0)/steps traj = [[x10,x20]] cdef double x1current = x10 cdef double x2current = x20 cdef int i cdef double newx1 cdef double newx2 for i in range(0,steps): newx1 = x1current + h*a11*x1current + h*a12*x2current newx2 = x2current + h*a21*x1current + h*a22*x2current if newx1 > cutoff or newx2 > cutoff or newx1 < -cutoff or newx2 < -cutoff: break traj.append([newx1,newx2]) x1current = newx1 x2current = newx2 return traj }}} {{{#!sagecell @interact def planarsystem(a11 = slider(srange(-10,10,1/10),default = -1), a12 = slider(srange(-10,10,1/10),default = -1), a21 = slider(srange(-10,10,1/10),default = 1), a22 = slider(srange(-10,10,1/10),default = -1), time_tracked = slider(srange(1,100,1.0),default=10)): A = matrix(RDF,[[a11,a12],[a21,a22]]) eigs = A.eigenvalues() html('<center>$x\' = Ax$ dynamics<BR>$A = '+latex(A)+'$, eigenvalues: $%2.2f + %2.2fI, %2.2f + %2.2fI$</center>'%(eigs[0].real(),eigs[0].imag(),eigs[1].real(),eigs[1].imag())) trajs = Graphics() for q in srange(0,2*pi,.15): astart = randint(1,10) ntraj = c_euler_m(0,cos(q),sin(q),time_tracked,300,a11,a12,a21,a22) for i in range(astart,len(ntraj)-1,10): trajs = trajs + arrow(ntraj[i],ntraj[i+1],width=1, arrowsize=2) trajs = trajs + line(ntraj) ntraj = c_euler_m(0,cos(q),sin(q),-time_tracked,300,a11,a12,a21,a22) trajs = trajs + line(ntraj) for i in range(astart,len(ntraj)-1,10): trajs = trajs + arrow(ntraj[i+1],ntraj[i],width=1, arrowsize=2) show(trajs, figsize = [6,6], xmin = -1, xmax = 1, ymin = -1, ymax = 1) }}} {{attachment:linear2x2.png}} |
|
| Line 132: | Line 175: |
| {{{ | {{{#!sagecell |
| Line 212: | Line 255: |
| {{{ | {{{#!sagecell |
| Line 258: | Line 301: |
| == Euler-Maruyama method and geometric Brownian motion (a common simple model of the stock market) == by Marshall Hampton {{{#!sagecell def EulerMaruyama(xstart, ystart, xfinish, nsteps, f1, f2): sol = [ystart] xvals = [xstart] h = N((xfinish-xstart)/nsteps) for step in range(nsteps): sol.append(sol[-1] + h*f1(sol[-1]) + h^(.5)*f2(sol[-1])*normalvariate(0,1)) xvals.append(xvals[-1] + h) return zip(xvals,sol) out = Graphics() save(out,DATA+'temp') @interact def EulerMaruyamaExample(mu = slider(srange(0,10,.1),default=2.0),sigma = slider(srange(0,10,.1),default=0.5),plots_at_a_time = slider(range(1,100),default=10), number_of_steps = slider(range(1,1000),default=100), clear_plot = checkbox(True), update=selector(['Update'],buttons =True, label='')): html('<center>Example of the Euler-Maruyama method applied to<br>the stochastic differential equation for geometric Brownian motion</center>') html('<center>$S = S_0 + \int_0^t \mu S dt + \int_0^t \sigma S dW$</center>') emplot = list_plot(EulerMaruyama(0,1,1,number_of_steps,lambda x: mu*x,lambda x:sigma*x),plotjoined=True) for i in range(1,plots_at_a_time): emplot = emplot + list_plot(EulerMaruyama(0,1,1,100,lambda x: mu*x,lambda x:sigma*x),plotjoined=True) if clear_plot: out = emplot save(out,DATA+'temp') else: out = load(DATA+'temp') out = out + emplot save(out,DATA+'temp') show(out, figsize = [8,5]) }}} {{attachment:eulermaruyama.png}} |
|
| Line 262: | Line 337: |
| {{{ | {{{#!sagecell |
| Line 288: | Line 363: |
| {{{ | {{{#!sagecell |
| Line 318: | Line 393: |
| {{{ | {{{#!sagecell |
| Line 326: | Line 401: |
| alpha=[(n,c*numerical_integral(f(x)*sin(x*n/2),0,2*pi)[0] ) for n in range(1,orden)] | alpha=[(n,c*numerical_integral(f*sin(x*n/2),0,2*pi)[0] ) for n in range(1,orden)] |
| Line 336: | Line 411: |
| == Heat equation using finite diferences in cython (very fast!) == | == Heat equation using finite diferences in cython == |
| Line 339: | Line 414: |
| {{{ | {{{#!sagecell |
| Line 355: | Line 430: |
| {{{ | {{{#!sagecell |
| Line 360: | Line 435: |
| def _(f=input_box(default=x*exp(-x^2)), longitud=input_box(default=2*pi), | def _(f=input_box(default=x*exp(-x^2),label='f(x)'), longitud=input_box(default=2*pi), |
| Line 363: | Line 438: |
| efe=f._fast_float_() | efe=f._fast_float_(x) |
| Line 382: | Line 457: |
| {{{ | {{{#!sagecell |
Sage Interactions - Differential Equations
goto interact main page
Contents
-
Sage Interactions - Differential Equations
- Euler's Method in one variable
- Vector Fields and Euler's Method
- Vector Field with Runga-Kutta-Fehlberg
- Linear two-dimensional ODEs
- Euler's Method, Improved Euler, and 4th order Runge-Kutta in one variable
- Mass/Spring systems
- Picard iteration example
- Euler-Maruyama method and geometric Brownian motion (a common simple model of the stock market)
- Autonomous equations and stable/unstable fixed points
- Heat equation using Fourier series
- Heat equation using finite diferences in cython
- DE with boundary values
Euler's Method in one variable
by Marshall Hampton. This needs some polishing but its usable as is.
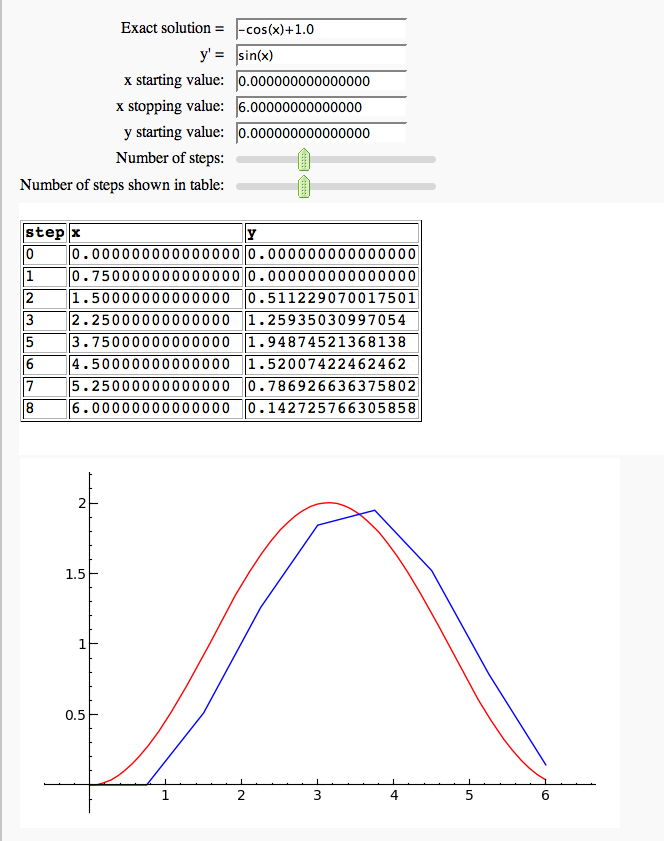
Vector Fields and Euler's Method
by Mike Hansen (tested and updated by William Stein, and later by Dan Drake)
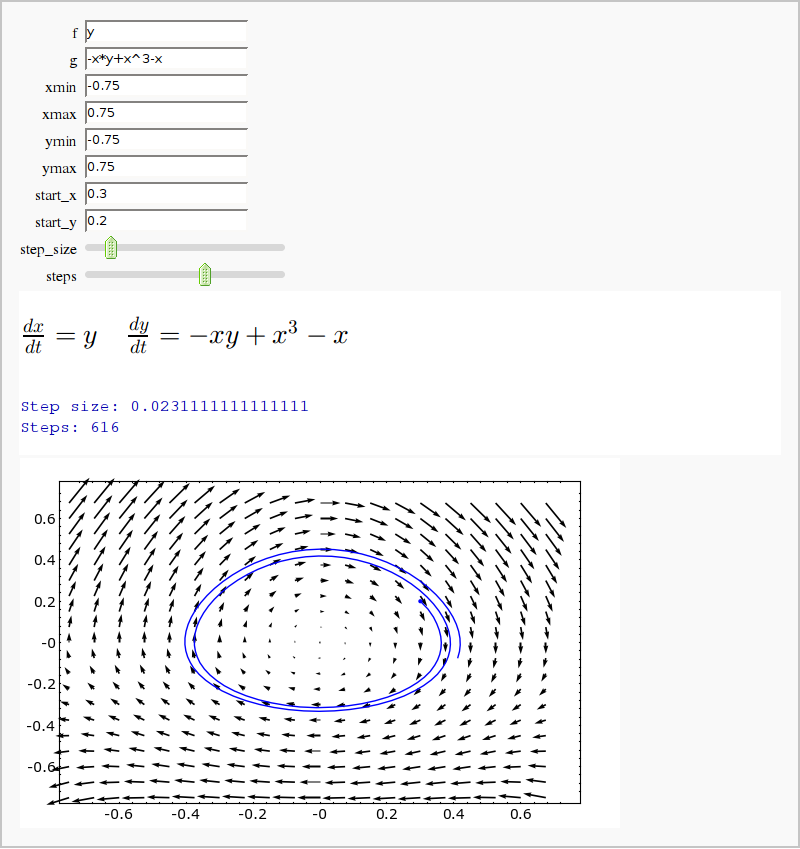
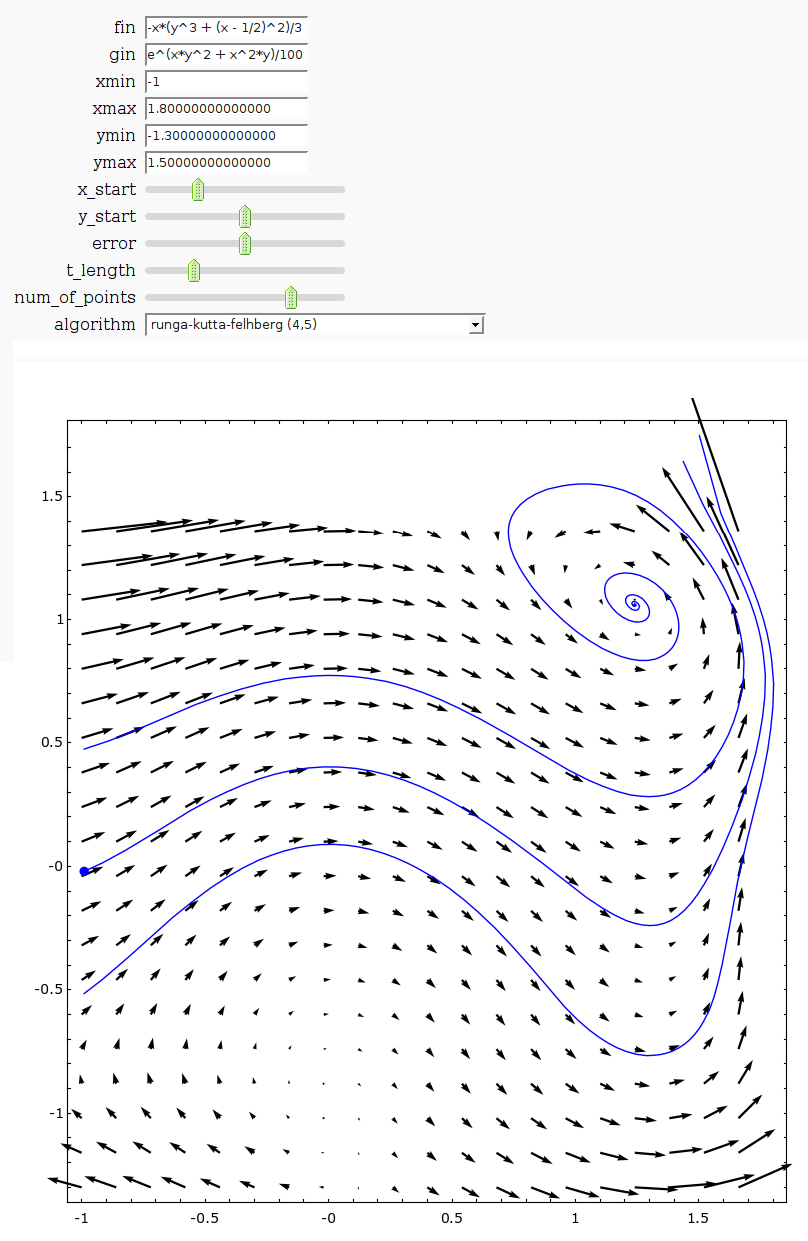
Vector Field with Runga-Kutta-Fehlberg
by Harald Schilly
Linear two-dimensional ODEs
by Marshall Hampton
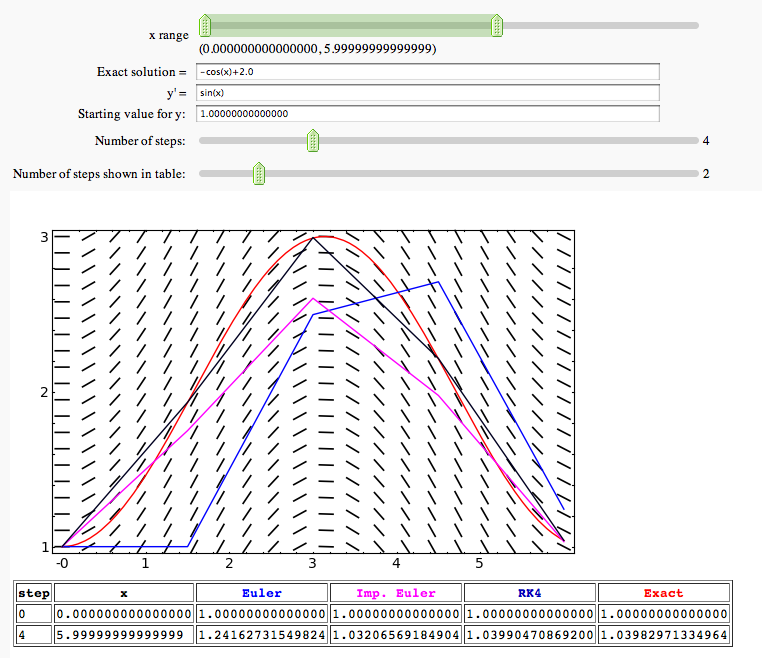
Euler's Method, Improved Euler, and 4th order Runge-Kutta in one variable
by Marshall Hampton. This is a more baroque version of the Euler's method demo above.
Mass/Spring systems
by Jason Grout
These two interacts involve some Cython code or other scipy imports, so I've posted a file containing them. You can download the worksheet or copy it online.
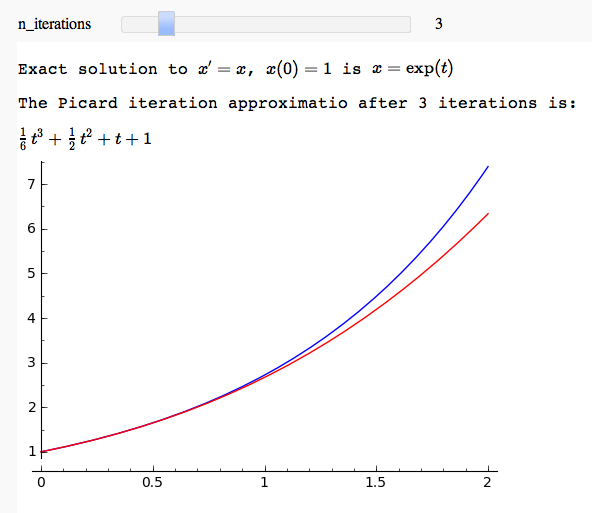
Picard iteration example
by Marshall Hampton and David Joyner
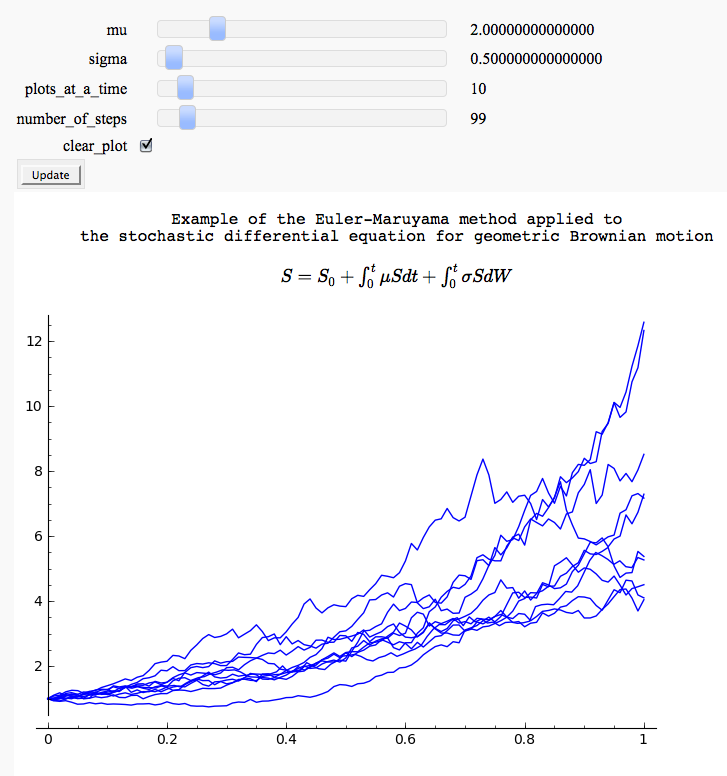
Euler-Maruyama method and geometric Brownian motion (a common simple model of the stock market)
by Marshall Hampton
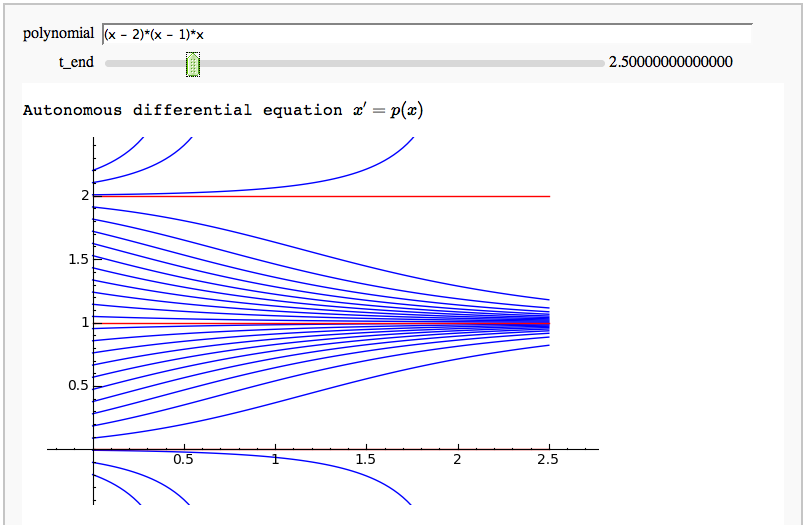
Autonomous equations and stable/unstable fixed points
by Marshall Hampton This needs the Cython functon defined in a seperate cell. Note that it is not a particularly good example of Cython use.
Heat equation using Fourier series
by Pablo Angulo
Heat equation using finite diferences in cython
by Pablo Angulo

DE with boundary values
The following interact demo looks at the DE+BC y'+y=0, y(0)=a, y(b)=c, and has a slider for b. When b=pi "problems arise":-)
