Graph Theory
Participants: Emily Kirkman, Robert Miller, Craig Citro and David Roe
# Cayley Graph of $A_5$ sage: G = sage.groups.perm_gps.permgroup.AlternatingGroup(5) sage: C = G.cayley_graph() sage: C.show3d(vertex_size=0.01, arc_size=0.005, arc_size2=0.008, xres=1000, yres=800)
BEFORE
AFTER

NEW
Vertex and edge colors for 3d graphs 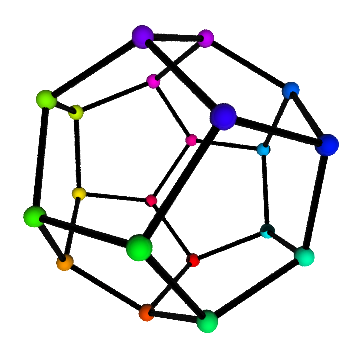

(done) Latex Graphs: Craig Citro & Robert Miller -- write an eps file to be included in LaTeX documents.
- (done) NetworkX 1: Expose these in SAGE: centrality, cliques, cluster, cores, search.
Also note significant updates to Generators class from wrapping NetworkX, (see the wiki for pretty pictures).
Wishlist from Chris Godsil. Most feasible first.
- (done) graph isomorphism and automorphism, graph6 and sparse6 formatting, database of small graphs, eigenvalues and eigenspaces, characteristic and minimal polynomials, cayley graphs, edge colorings
- (easy) bipartite graphs, point graph, line graph, graph from set and binary function, vertices as vector subspaces, generating trees
- (medium) certain types of curves for plotting edges, generator based on geng
- (tedium) databases: ted spence, gordon royle
- (hard) max indep. set, chromatic number, hamilton cycles and paths, chromatic polynomial, tutte polynomial, cut vertices, vertex/edge connectivity, planarity
- Graph Database: Update interface to sqlite database of all graphs with 8 or fewer vertices.
- Emily Kirkman is currently working on this.
Electrical Networks, Jim Morrow's REU: Graphs with boundary are already in sage, but there are probably some useful constructions for Jim's summer REU that are not implemented yet. Especially data structures, perhaps an ElectricalNetworks class. Look at the Dirichlet problem, graphs on surfaces and (circular) planar embeddings of graphs.
- Bipartite Class
- NetworkX 2:
- spectrum -- This should probably not be wrapped, but instead mimicked, since sage's linear algebra is undoubtedly faster.
- hybrid, threshold -- Figure out what these are?
