|
Size: 2133
Comment: FLINT, arb
|
Size: 37052
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 3: | Line 3: |
| Current development cycle (2022) | Release candidate (2022) |
| Line 7: | Line 7: |
| == User interface, plotting and graphics == === JupyterLab 3.3 === [[https://jupyter.org/|JupyterLab]], the latest web-based interactive development environment for notebooks, code, and data, is slated to replace the now-classic Jupyter notebook interface. The version of !JupyterLab in the Sage distribution has been upgraded to the major new version 3.3. [[https://trac.sagemath.org/ticket/32069|#32069]], [[https://trac.sagemath.org/ticket/33607|#33607]] After `./sage -i jupyterlab_widgets`, you can run it using {{{ ./sage -n jupyterlab }}} Also two new interface variants are provided: {{{ ./sage -n nbclassic }}} and {{{ ./sage -n retrolab }}} === Interactive graph editing with phitigra === With the new optional package [[https://pypi.org/project/phitigra|phitigra]] (use `./sage -i phitigra` to install), graphs can be edited by interactively placing vertices, edges, etc. This works both in the classic Jupyter notebook and in !JupyterLab. === Hyperbolic plots === * Added the ability to choose the hyperbolic model for hyperbolic plots. [[https://trac.sagemath.org/ticket/22081|#22081]] === Graphics with TikZ === The `TikzPicture` module which was developed in the [[https://pypi.org/project/slabbe/|slabbe]] package for more than 5 years is now in Sage. This was done in ticket [[https://trac.sagemath.org/ticket/20343|#20343]]. Below are some usage examples. First example shows that it takes any tikz picture string as input: {{{ sage: from sage.misc.latex_standalone import TikzPicture sage: s = '\\begin{tikzpicture}\n\\draw[->,green,very thick](0,0) -- (1,1);\\end{tikzpicture}' sage: t = TikzPicture(s) sage: t # in Jupyter, rich representation will show the image instead \documentclass[tikz]{standalone} \begin{document} \begin{tikzpicture} \draw[->,green,very thick](0,0) -- (1,1);\end{tikzpicture} \end{document} sage: path_to_file = t.pdf() # and opens the image in a viewer }}} {{attachment:tikz_arrow.png}} Of course, conversion to pdf format necessitates `pdflatex` or `lualatex`. If `lualatex` is available it uses it in preference to `pdflatex` because it handles better the very big pictures in terms of memory limits. One can provide a local filename to save to, or convert the image to other formats (using pdftocairo or imagemagick external packages): {{{ sage: path_to_file = t.pdf('file.pdf') # when providing a filename, it just saves the file locally, does not open in a viewer sage: path_to_file = t.png() # conversion to png sage: path_to_file = t.svg() # to svg sage: path_to_file = t.tex() # print the tex source to a file }}} Another example with graphs where additional usepackage are necessary to compile the image correctly: {{{ sage: from sage.misc.latex_standalone import TikzPicture sage: g = graphs.PetersenGraph() sage: t = TikzPicture(latex(g), standalone_config=["border=4mm"], usepackage=['tkz-graph']) sage: t # in Jupyter, rich representation will show the image instead \documentclass[tikz]{standalone} \standaloneconfig{border=4mm} \usepackage{tkz-graph} \begin{document} \begin{tikzpicture} \definecolor{cv0}{rgb}{0.0,0.0,0.0} \definecolor{cfv0}{rgb}{1.0,1.0,1.0} \definecolor{clv0}{rgb}{0.0,0.0,0.0} \definecolor{cv1}{rgb}{0.0,0.0,0.0} --- 65 lines not printed (3695 characters in total). Use print to see the full content. --- \Edge[lw=0.1cm,style={color=cv6v8,},](v6)(v8) \Edge[lw=0.1cm,style={color=cv6v9,},](v6)(v9) \Edge[lw=0.1cm,style={color=cv7v9,},](v7)(v9) % \end{tikzpicture} \end{document} sage: _ = t.pdf() # or t.png() or t.svg() }}} {{attachment:tikz_graph.png}} {{{ sage: from sage.misc.latex_standalone import TikzPicture sage: V = [[1,0,1],[1,0,0],[1,1,0],[0,0,-1],[0,1,0],[-1,0,0],[0,1,1],[0,0,1],[0,-1,0]] sage: P = Polyhedron(vertices=V).polar() sage: s = P.projection().tikz([674,108,-731],112) sage: t = TikzPicture(s) sage: _ = t.pdf() # or t.png() or t.svg() }}} {{attachment:tikz_polyhedron.png}} The module also contains a class `Standalone`, from which the class `TikzPicture` inherits: {{{ sage: from sage.misc.latex_standalone import Standalone sage: s = Standalone('Hello World', usepackage=['amsmath'], standalone_config=['beamer=true','border=1mm']) sage: s # in Jupyter, rich representation will show the image instead \documentclass{standalone} \standaloneconfig{beamer=true} \standaloneconfig{border=1mm} \usepackage{amsmath} \begin{document} Hello World \end{document} sage: _ = s.pdf() # or s.png() or s.svg() }}} {{attachment:tikz_hello.png}} Another example using `Standalone` with a tableau: {{{ sage: P = Permutations(10) sage: p = P.random_element() sage: p [3, 10, 1, 9, 5, 6, 7, 2, 8, 4] sage: t = p.to_tableau_by_shape([3,3,3,1]) sage: t [[2, 8, 4], [5, 6, 7], [10, 1, 9], [3]] sage: s = Standalone(latex(t), standalone_config=["border=1mm"]) sage: s \documentclass{standalone} \standaloneconfig{border=1mm} \begin{document} {\def\lr#1{\multicolumn{1}{|@{\hspace{.6ex}}c@{\hspace{.6ex}}|}{\raisebox{-.3ex}{$#1$}} } \raisebox{-.6ex}{$\begin{array}[b]{*{3}c}\cline{1-3} \lr{2}&\lr{8}&\lr{4}\\\cline{1-3} \lr{5}&\lr{6}&\lr{7}\\\cline{1-3} \lr{10}&\lr{1}&\lr{9}\\\cline{1-3} \lr{3}\\\cline{1-1} \end{array}$} } \end{document} sage: _ = s.pdf() # or s.png() or s.svg() }}} {{attachment:tikz_tableau.png}} In a next step, a method `tikz()` will be added to graphs, polytopes, posets, etc. to return an object of type `TikzPicture` see [[https://trac.sagemath.org/ticket/33002|#33002]]. === Complex plots === The complex plotting package [[https://github.com/davidlowryduda/phase_mag_plot|phase_mag_plot]] has been incorporated into Sage. Now `complex_plot` allows contouring, tiling, and `matplotlib`-compatible colormaps. This was added in ticket [[https://trac.sagemath.org/ticket/33416|#33416]]. To use a colormap, one can pass in a string as in {{{ sage: complex_plot((x - 5)*sqrt(x), (-10, 10), (-10, 10), cmap='twilight') }}} {{attachment:cmap_twilight.png}} Contouring or tiling are enabled through keyword options. To look smooth, it's typically necessary to plot the function on additional points through the use of `plot_points`. This looks like {{{ sage: complex_plot((x - 5)*sqrt(x), (-10, 10), (-10, 10), cmap='twilight', plot_points=500, contoured=True) }}} {{attachment:cmap_twilight_contour.png}} {{{ sage: complex_plot((x - 5)*sqrt(x), (-10, 10), (-10, 10), cmap='twilight', plot_points=500, tiled=True) }}} {{attachment:cmap_twilight_tiled.png}} === LaTeX displays in JupyterLab === Users of Sage in [[https://jupyter.org/|JupyterLab]] got used to expressions displayed at center in the LaTeX display mode. For compatibility with displays in classic Jupyter, we decided to change the behavior so that now expressions are displayed aligned left by default. If you belong to the minority preferring centered displays, you can set your preference by {{{ dm = get_display_manager() dm.preferences.align_latex = 'center' # or 'left' }}} in the `~/.sage/init.sage` script. === Other improvements === [[https://trac.sagemath.org/ticket/33469|#33469]] == Linear Algebra == === NumPy integration === The new classes `Matrix_numpy_integer_dense` and `Vector_numpy_integer_dense` implement matrices and vectors with 64-bit integer entries backed by `numpy` arrays. [[https://trac.sagemath.org/ticket/32465|#32465]]. As a first application, several methods of `GenericGraph` that return matrices, such as `adjacency_matrix`, now accept keyword arguments that can select the matrix implementation. [[https://trac.sagemath.org/ticket/33377|#33377]], [[https://trac.sagemath.org/ticket/33387|#33387]], [[https://trac.sagemath.org/ticket/33388|#33388]], [[https://trac.sagemath.org/ticket/33389|#33389]] {{{ sage: graphs.PathGraph(5).adjacency_matrix(sparse=False, implementation='numpy') [0 1 0 0 0] [1 0 1 0 0] [0 1 0 1 0] [0 0 1 0 1] [0 0 0 1 0] sage: type(_) <class 'sage.matrix.matrix_numpy_integer_dense.Matrix_numpy_integer_dense'> }}} === CombinatorialFreeModule improvements === Performing sums and similar constructions for `CombinatorialFreeModule` have been made faster. [[https://trac.sagemath.org/ticket/33267|#33267]] == Symbolics == === SymPy 1.10.1 === !SymPy has been upgraded to version 1.10.1 ([[https://github.com/sympy/sympy/wiki/release-notes-for-1.10|release notes]]). [[https://trac.sagemath.org/ticket/33398|#33398]], [[https://trac.sagemath.org/ticket/33547|#33547]], [[https://trac.sagemath.org/ticket/33584|#33584]] === ImageSet === Sage 9.6 defines a new class `ImageSet`. [[https://trac.sagemath.org/ticket/32121|#32121]] {{{ sage: ImageSet(sin, RealSet.open(0, pi/4)) Image of (0, 1/4*pi) by The map sin from (0, 1/4*pi) sage: _.an_element() 1/2*sqrt(-sqrt(2) + 2) sage: sos(x,y) = x^2 + y^2; sos (x, y) |--> x^2 + y^2 sage: ImageSet(sos, ZZ^2) Image of Ambient free module of rank 2 over the principal ideal domain Integer Ring by The map (x, y) |--> x^2 + y^2 from Vector space of dimension 2 over Symbolic Ring sage: _.an_element() 1 sage: ImageSet(sos, Set([(3, 4), (3, -4)])) Image of {...(3, -4)...} by The map (x, y) |--> x^2 + y^2 from Vector space of dimension 2 over Symbolic Ring sage: _.an_element() 25 }}} The new class mirrors and translates to [[https://docs.sympy.org/latest/modules/sets.html#imageset|SymPy's ImageSet]]: {{{ sage: from sage.sets.image_set import ImageSet sage: S = ImageSet(sin, RealSet.open(0, pi/4)); S Image of (0, 1/4*pi) by The map sin from (0, 1/4*pi) sage: S._sympy_() ImageSet(Lambda(x, sin(x)), Interval.open(0, pi/4)) }}} Most methods of `ImageSet` are actually provided by its base class, the new class `ImageSubobject`. For all morphisms in the `Sets` category, there is now a default method `image`, which constructs an instance of either `ImageSubobject` or `ImageSet`. === Orthogonal polynomials === Three classes of classical (discrete) orthogonal polynomials in the Askey scheme have been added: [[https://trac.sagemath.org/ticket/33393|#33393]] * Krawtchouk polynomials * Hahn polynomials * Meixner polynomials == Polyhedral geometry and linear programming == === polymake 4.6 === polymake, a comprehensive system for computations in polyhedral geometry, tropical geometry, etc., has been upgraded to version 4.6 ([[https://polymake.org/doku.php/news/release_4_6|release notes]]). [[https://trac.sagemath.org/ticket/33251|#33251]] === CyLP === The new optional package [[https://github.com/coin-or/CyLP|CyLP]] (`./sage -i cylp`) provides a detailed interface to [[https://github.com/coin-or/Clp|Clp]], the COIN-OR linear programming solver, and [[https://github.com/coin-or/Cbc|Cbc]], the COIN-OR branch-and-cut solver for mixed-integer linear programs. [[https://trac.sagemath.org/ticket/33487|#33847]] In a future version of Sage, CyLP is intended to provide a replacement for the Sage-specific backend interface to Clp and Cbc, [[https://pypi.org/project/sage-numerical-backends-coin/|sage-numerical-backends-coin]]; see [[https://trac.sagemath.org/ticket/26511|Meta-ticket #26511]]. === Equivariant Ehrhart theory === [[https://trac.sagemath.org/ticket/27637|#27637]] |
|
| Line 9: | Line 277: |
| === Improved Manifold constructor === The `structure` parameter of the `Manifold` constructor has new, more convenient defaulting behavior. [[https://trac.sagemath.org/ticket/33001|#33001]] When parameters such as `diff_degree` or `metric_name` are given, the implied structure is selected: {{{ sage: M = Manifold(3, 'M', diff_degree=0); M 3-dimensional topological manifold M sage: M = Manifold(3, 'M', diff_degree=2); M 3-dimensional differentiable manifold M sage: M = Manifold(3, 'M', metric_name='g'); M 3-dimensional Riemannian manifold M }}} |
|
| Line 13: | Line 295: |
| === Projective spaces === Real projective spaces have been added to the manifold catalog ([[https://trac.sagemath.org/ticket/33221|#33221]]). For example, one can construct the real projective plane. {{{ sage: RP2 = manifolds.RealProjectiveSpace(); RP2 2-dimensional topological manifold RP2 sage: latex(RP2) \mathbb{RP}^{2} }}} There are three charts. Considering an immersion in three-dimensional Euclidean space, the chart corresponds to a choice of one (out of three possible) coordinates to be always nonzero. The coordinates listed are the two other coordinates assuming that the nonzero coordinate is always one. {{{ sage: C0, C1, C2 = RP2.top_charts() sage: p = RP2.point((2,0), chart = C0) sage: q = RP2.point((0,3), chart = C0) sage: p in C0.domain() True sage: p in C1.domain() True sage: C1(p) (1/2, 0) sage: p in C2.domain() False sage: q in C0.domain() True }}} The point `q` looks like `(1,0,3)` in ambient Euclidean space, so it is not in the domain of the chart `C1`. It also has the form `(1/3,0,1)` when considered in the chart `C2`. {{{ sage: q in C1.domain() False sage: q in C2.domain() True sage: C2(q) (1/3, 0) }}} If both coordinates in a local chart are nonzero then that point is in the domain of all charts. The change of coordinates is found by normalizing the appropriate chart. So for example, the point `(1, 2, 3)` is the same as the point `(1/2, 1, 3/2)` is the same as the point `(1/3, 2/3, 1)`, which is reflected by defining `r` to be a point in the default chart `C0`. {{{ sage: r = RP2.point((2,3)) sage: r in C0.domain() and r in C1.domain() and r in C2.domain() True sage: C0(r) # corresponding to (1, 2, 3) (2, 3) sage: C1(r) # corresponding to (1/2, 1, 3/2) (1/2, 3/2) sage: C2(r) # corresponding to (1/3, 2/3, 1) (1/3, 2/3) }}} == Algebra == === lrcalc 2.1 === lrcalc, Anders Buch's Littlewood-Richardson Calculator, has been upgraded to the major new version 2.1 [[https://bitbucket.org/asbuch/lrcalc/src/master/ChangeLog|changelog]]. [[https://trac.sagemath.org/ticket/31355|#31355]] === Finitely presented modules over graded algebras === Sage 9.6 allows the construction of finitely presented modules over graded algebras, even algebras which are infinite and/or noncommutative like the mod ''p'' Steenrod algebra. Some homological algebra is implemented in general, and more tools are implemented specifically for modules over the Steenrod algebra ([[https://trac.sagemath.org/ticket/32505|#32505]], [[https://trac.sagemath.org/ticket/30680|#30680]]). {{{ sage: from sage.modules.fp_graded.module import FPModule sage: E.<x,y> = ExteriorAlgebra(QQ) # M has one generator g in degree 0 and two relations, x*g and y*g. # That is, M is QQ as a trivial E-module. sage: M = FPModule(E, [0], [[x], [y]]) # Free resolution: sage: M.resolution(3) [Module morphism: From: Free graded left module on 1 generator over The exterior algebra of rank 2 over Rational Field To: Finitely presented left module on 1 generator and 2 relations over The exterior algebra of rank 2 over Rational Field Defn: g[0] |--> g[0], Module morphism: From: Free graded left module on 2 generators over The exterior algebra of rank 2 over Rational Field To: Free graded left module on 1 generator over The exterior algebra of rank 2 over Rational Field Defn: g[1, 0] |--> x*g[0] g[1, 1] |--> y*g[0], Module morphism: From: Free graded left module on 3 generators over The exterior algebra of rank 2 over Rational Field To: Free graded left module on 2 generators over The exterior algebra of rank 2 over Rational Field Defn: g[2, 0] |--> x*g[1, 0] g[2, 1] |--> y*g[1, 0] + x*g[1, 1] g[2, 2] |--> y*g[1, 1], Module morphism: From: Free graded left module on 4 generators over The exterior algebra of rank 2 over Rational Field To: Free graded left module on 3 generators over The exterior algebra of rank 2 over Rational Field Defn: g[3, 0] |--> x*g[2, 0] g[3, 1] |--> y*g[2, 0] + x*g[2, 1] g[3, 2] |--> y*g[2, 1] + x*g[2, 2] g[3, 3] |--> y*g[2, 2]] }}} There is a new thematic tutorial providing many details and examples. === Miscellaneous improvements === * Ideal membership over quotient rings can now be decided (by reducing to ideal membership in the parent ring). [[https://trac.sagemath.org/ticket/33237|#33237]] * Iterating over (some) infinite modules (including ''ℤ^n'') now enumerates the entire module, in a "natural" order. [[https://trac.sagemath.org/ticket/33287|#33287]] * `BinaryQF.solve_integer()` now also works for quadratic forms of square discriminant. [[https://trac.sagemath.org/ticket/33026|#33026]] * `Quaternion fractional ideals` (including orders) now support the usual operations (e.g., `a*I`, `I*a`, `I+J`). [[https://trac.sagemath.org/ticket/32264|#32264]] * `AdditiveAbelianGroupWrapper` now exposes `.discrete_log()` for (multi-dimensional) logarithms in finite abelian groups. [[https://trac.sagemath.org/ticket/32384|#32384]] * Graded submodules of graded modules now know they are graded (with respect to the ambient grading); similarly for filtered submodules. [[https://trac.sagemath.org/ticket/33321|#33321]] * Polynomials now evaluate faster on monomial inputs. [[https://trac.sagemath.org/ticket/33165|#33165]] * Implement specialized code for summing terms and monomials in `CombinatorialFreeModule`. [[https://trac.sagemath.org/ticket/33267|#33267]] * Improvements and fixes to `skew_by()` in symmetric functions. [[https://trac.sagemath.org/ticket/33313|#33313]] * Attempt to invert elements generically in a finite dimensional algebra. [[https://trac.sagemath.org/ticket/33250|#33250]] * Tensor products of finite dimensional modules know they are finite dimensional (Sage does not currently have any structure for infinite tensor products, which can have some subtleties). [[https://trac.sagemath.org/ticket/30252|#30252]] * Improved coercions and conversions with Laurent polynomials and their fraction field. [[https://trac.sagemath.org/ticket/31320|#31320]] [[https://trac.sagemath.org/ticket/33477|#33477]] * Faster evaluation of univariate polynomials with monomials. [[https://trac.sagemath.org/ticket/33165|#33165]] == Number theory == === Elliptic curves === * Elliptic-curve DLP and Weil pairings over finite fields are now ''much'' faster (thanks to PARI). [[https://trac.sagemath.org/ticket/33121|#33121]] * Scalar multiplication on elliptic curves over finite fields is now significantly faster (thanks to PARI). [[https://trac.sagemath.org/ticket/33147|#33147]] * Computing the Weierstraß ℘ function of an elliptic curve is now significantly faster (thanks to PARI). [[https://trac.sagemath.org/ticket/33223|#33223]] * Classes used by the Monsky-Washnitzer curves now use the new coercion system. [[https://trac.sagemath.org/ticket/33525|#33525]] [[https://trac.sagemath.org/ticket/33576|#33576]] == Coding theory == Optimizations to `SBox`. [[https://trac.sagemath.org/ticket/25633|#25633]] |
|
| Line 19: | Line 445: |
| === FLINT and arb === FLINT from 2.7.1 to 2.8.4, arb to 2.22.1 [[https://trac.sagemath.org/ticket/32211|#32211]], [[https://trac.sagemath.org/ticket/33189|#33189]] The FLINT 2.8 series brings major new algorithms and general speedups. [[https://github.com/wbhart/flint2/blob/flint-2.8/NEWS#L1262]] |
=== Python 3.10 === Sage 9.6 continues to support system Python 3.7.x to 3.10.x. If no suitable version of Python is installed in the system, Sage will install its own copy of Python. Sage now ships Python 3.10.3 for this purpose. [[https://trac.sagemath.org/ticket/30767|#30767]], [[https://trac.sagemath.org/ticket/33512|#33512]] === FLINT 2.8.x and arb 2.22.x === [[https://flintlib.org/|FLINT]] has been upgraded from 2.7.1 to 2.8.4.[[https://trac.sagemath.org/ticket/32211|#32211]] The FLINT 2.8 series brings major new algorithms and general speedups ([[https://github.com/wbhart/flint2/blob/flint-2.8/NEWS#L1262|release notes]]). |
| Line 28: | Line 459: |
| [[https://arblib.org/|arb]] has been upgraded from 2.19.0 to 2.22.1. [[https://trac.sagemath.org/ticket/32211|#32211]], [[https://trac.sagemath.org/ticket/33189|#33189]] The 2.20, 2.21, and 2.22 series have brought major new algorithms and other improvements ([[https://arblib.org/history.html#version-2-22-1|changelog]]). === igraph 0.9.x === The `igraph` library and its Python interface (now also just called `igraph`) have been upgraded to versions 0.9.7/0.9.9. [[https://trac.sagemath.org/ticket/32510|#32510]], [[https://trac.sagemath.org/ticket/33526|#33526]] == For developers: Refactoring and modularization == See also [[https://trac.sagemath.org/ticket/29705|Meta-ticket #29705]] === sage.features.Executable.absolute_filename() === The Sage library interfaces to some external non-Python packages by running an executable program in a separate process. The package may either be available from a system installation, or the Sage distribution may have installed the package in the `SAGE_LOCAL` prefix hierarchy. The main `sage` script sets up various environment variables before starting the Python interpreter; in particular, it sets `PATH` to include `SAGE_LOCAL/bin`, which ensures that the installed executables are found. In Sage 9.6, we have changed most calls to executables so that they no longer depend on the environment variable `PATH` being set in this way. Every executable program is represented by an instance of `sage.features.Executable`. Its method `absolute_filename` explicitly searches inside `SAGE_LOCAL/bin` (in installations with `SAGE_LOCAL`) before it depends on `PATH`. [[https://trac.sagemath.org/ticket/31292|#31292]], [[https://trac.sagemath.org/ticket/31296|#31296]], [[https://trac.sagemath.org/ticket/32645|#32645]], [[https://trac.sagemath.org/ticket/32893|#32893]], [[https://trac.sagemath.org/ticket/33440|#33440]], [[https://trac.sagemath.org/ticket/33465|#33465]], [[https://trac.sagemath.org/ticket/33467|#33467]] === Preparations for PEP 420 implicit namespace packages === The Sage doctester is now prepared for [[https://doc.sagemath.org/html/en/developer/packaging_sage_library.html#ordinary-packages-vs-implicit-namespace-packages|namespace packages]]. [[https://trac.sagemath.org/ticket/33033|#33033]] To [[https://doc.sagemath.org/html/en/developer/packaging_sage_library.html#module-level-runtime-dependencies|reduce runtime dependencies]], many imports from `sage.graphs.all`, `sage.interfaces.all`, `sage.misc.all`, `sage.libs.all`, `sage.rings.all` have been replaced by more specific imports; and module-level imports from `sage.plot` have been changed to either use `lazy_import` or have been moved inside methods. [[https://trac.sagemath.org/ticket/30582|#30582]], [[https://trac.sagemath.org/ticket/32847|#32847]], [[https://trac.sagemath.org/ticket/32989|#32989]], [[https://trac.sagemath.org/ticket/32999|#32999]], [[https://trac.sagemath.org/ticket/33000|#33000]], [[https://trac.sagemath.org/ticket/33007|#33007]], [[https://trac.sagemath.org/ticket/33146|#33146]], [[https://trac.sagemath.org/ticket/33199|#33199]], [[https://trac.sagemath.org/ticket/33466|#33466]], [[https://trac.sagemath.org/ticket/33468|#33468]] === Lazy imports of classes now support __instancecheck__ and __subclasscheck__ === No Python object is an instance of a class that cannot be imported from the module that defines it. The new special method `LazyImport.__instancecheck__` now just returns `False` in this case. [[https://trac.sagemath.org/ticket/33017|#33017]] This provides a convenient pattern for writing modularized code when [[https://wiki.sagemath.org/ReleaseTours/sage-9.5#Abstract_base_classes_for_.22isinstance.22_testing|creating an abstract base class for "isinstance" testing]] is not justified. {{{ sage: from sage.schemes.generic.scheme import Scheme sage: sZZ = Scheme(ZZ) sage: lazy_import('xxxx_does_not_exist', 'Pluffe') sage: isinstance(sZZ, (Scheme, Pluffe)) True sage: isinstance(ZZ, (Scheme, Pluffe)) False }}} Likewise, no class is a subclass of a class that cannot be imported from the module that defines it; so the new special method `LazyImport.__subclasscheck__` implements the same logic. === sage.geometry.polyhedron.base reorganized === The module `sage.geometry.polyhedron.base` has been split into several modules, grouping the methods of class `Polyhedron_base` according to their topic and runtime dependencies on other parts of Sage. [[https://trac.sagemath.org/ticket/32651|#32651]] == New developer tools == === Pre-built Docker containers on ghcr.io === Our portability CI on !GitHub Actions builds [[https://github.com/orgs/sagemath/packages?tab=packages&q=with-targets-optional|Docker images]] for all tested Linux platforms (and system package configurations) and makes them available on !GitHub Packages (ghcr.io). [[https://trac.sagemath.org/ticket/30933|#39033]] Since 9.6.beta1, the image version corresponding to the latest development release receives the additional Docker tag `dev`, see for example the Docker image for [[https://github.com/sagemath/sage/pkgs/container/sage%2Fsage-docker-ubuntu-impish-standard-with-targets-optional|ubuntu-impish-standard]]. Thus, for example, the following command will work: {{{ $ docker run -it ghcr.io/sagemath/sage/sage-docker-ubuntu-impish-standard-with-targets-optional:dev bash }}} Images whose names end with the suffix `-with-targets-optional` are the results of full builds and a run of `make ptest`. They also contain a copy of the source tree and the full logs of the build and test. [[https://github.com/orgs/sagemath/packages?tab=packages&q=sage-docker-debian-bullseye-standard|Smaller images corresponding to earlier build stages]] are also available: * `-with-system-packages` provides a system installation with system packages installed, no source tree, * `-configured` contains a partial source tree and has completed bootstrap and the `configure`, * `-with-targets-pre` contains the full source tree and a full installation of all non-Python packages, * `-with-targets` contains the full source tree and a full installation of Sage, including the HTML documentation, but `make ptest` has not been run yet. === Sage development in the cloud with Gitpod === [[https://www.gitpod.io/|Gitpod]] is a service that provides a development environment in the cloud based on VS Code. It is free to use for up to 50 hours per month. Sage now includes a configuration for Gitpod; see the new section [[https://620901c077fb7caa9f914f33--sagemath-tobias.netlify.app/developer/workspace.html#section-gitpod|Setting up your workspace]] in the Sage Developer's Guide. [[https://trac.sagemath.org/ticket/33103|#33103]], [[https://trac.sagemath.org/ticket/33589|#33589]] To launch Gitpod on a branch of a Trac ticket, you can use the new Gitpod badge in the ticket box. === Linting workflow (pycodestyle, relint) on GitHub Actions === A [[https://github.com/sagemath/sage/blob/develop/.github/workflows/lint.yml|linting workflow]] on !GitHub Actions runs on all pushes to a branch on Trac. It checks that the code of the current branch adheres to the style guidelines using [[https://doc.sagemath.org/html/en/developer/tools.html#pycodestyle|pycodestyle]] (in the `pycodestyle-minimal` configuration) and [[https://doc.sagemath.org/html/en/developer/tools.html#relint|relint]]. In order to see details when it fails, you can click on the badge and then select the most recent workflow run. Sage 9.6 includes again many improvements to the [[https://pycodestyle.pycqa.org/en/latest/intro.html#error-codes|coding style checked by pycodestyle]]. [[https://trac.sagemath.org/ticket/32978|#32978]], [[https://trac.sagemath.org/ticket/32979|#32979]], [[https://trac.sagemath.org/ticket/33095|#33095]], [[https://trac.sagemath.org/ticket/33102|#33102]], ... Consequently, the `pycodestyle-minimal` configuration has been extended to enforce `E111`, `E401`, `E701`, `E702`, `E703`, `W605`, `E711`, `E712`, `E713`, `E721`, `E722`. === Automatic incremental build for ticket branches on GitHub Actions === The [[https://github.com/sagemath/sage/blob/develop/.github/workflows/build.yml|build & test workflow]] on !GitHub Actions builds Sage for the current branch (incrementally on top of the system packages of the develop branch) and runs the test. Details are again available by clicking on the badge. Note that in contrast to the patchbot, the ticket branch is not merged into the current beta version. === Automatic documentation build for ticket branches on GitHub Actions === The [[https://github.com/sagemath/sage/blob/develop/.github/workflows/doc-build.yml|build documentation workflow]] on !GitHub Actions builds the HTML documentation for the current branch. If you click on the badge, you get the HTML output of the successful run. The idea is to use this to easily inspect changes to the documentation without the need to locally rebuild the docs yourself. If the doc build fails, you can go to [[https://github.com/sagemath/sagetrac-mirror/actions/workflows/doc-build.yml|the Actions tab of sagemath/sagetrac-mirror repo]] and choose the particular branch to see what went wrong. The idea is that these three status badges complement the existing patchbots (and maybe even replace them in the future). In particular, they are supposed to always be green. === Codecov === [[https://trac.sagemath.org/ticket/33355|#33355]] === sage --pytest === After the optional package [[https://docs.pytest.org/en/7.1.x/|pytest]] is installed (`./sage -i pytest`), a new command `./sage --pytest` is available, which runs pytest on the Sage library sources. [[https://trac.sagemath.org/ticket/33572|#33572]] Also the Sage doctester (`./sage -t` or `./sage -tox -e doctest`) invokes `pytest`. This functionality has been improved in Sage 9.6. [[https://trac.sagemath.org/ticket/31924|#31924]], [[https://trac.sagemath.org/ticket/32975|#32975]] === sage -t --baseline-stats-path === [[https://trac.sagemath.org/ticket/33233|#33233]] === Sage patchbot on GitHub Actions === The [[https://wiki.sagemath.org/patchbot#Running_the_patchbot_on_GitHub_Actions|Sage patchbot can now be run on GitHub Actions]], on top of any of the Linux platforms for which we have prebuilt Docker images.[[https://trac.sagemath.org/ticket/33253|#33253]] |
|
| Line 32: | Line 601: |
The Sage source code is available in the [[https://github.com/sagemath/sage/tree/9.5|sage git repository]]. |
The first release candidate, 9.6.rc0, was tagged on 2022-04-10. The [[https://6212659123a9467b3cb0cd07--sagemath-tobias.netlify.app/installation/index.html|SageMath installation guide]] now provides a decision tree that guides users and developers to a type of installation suitable for their system and their needs. === Sources === The Sage source code is available in the [[https://github.com/sagemath/sage/tree/develop|sage git repository]]. !SageMath 9.6 supports all [[https://wiki.sagemath.org/ReleaseTours/sage-9.5#Sources|platforms that were supported by Sage 9.5]] and '''adds support for building on distributions that use the (unreleased) [[https://gcc.gnu.org/gcc-12/changes.html|GCC 12]] series''' (`fedora-36`). [[https://trac.sagemath.org/ticket/33187|#33187]] * '''Linux 64-bit''' (x86_64) * ubuntu-{[[https://launchpad.net/ubuntu/trusty|trusty]]⁺,[[https://launchpad.net/ubuntu/xenial|xenial]],[[https://launchpad.net/ubuntu/bionic|bionic]],[[https://launchpad.net/ubuntu/focal|focal]],[[https://launchpad.net/ubuntu/hirsute|hirsute]],[[https://launchpad.net/ubuntu/impish|impish]],[[https://launchpad.net/ubuntu/jammy|jammy]]} * debian-{[[https://wiki.debian.org/DebianStretch|stretch]], [[https://wiki.debian.org/DebianBuster|buster]],[[https://wiki.debian.org/DebianBullseye|bullseye]],[[https://wiki.debian.org/DebianBookworm|bookworm]],[[https://wiki.debian.org/DebianUnstable|sid]]} * linuxmint-{[[https://www.linuxmint.com/edition.php?id=158|17]]⁺,[[https://www.linuxmint.com/edition.php?id=217|18]],[[https://linuxmint.com/rel_tara_cinnamon.php|19]],[[https://linuxmint.com/rel_tricia_cinnamon.php|19.3]],[[https://www.linuxmint.com/rel_ulyssa_cinnamon_whatsnew.php|20.1]],[[https://linuxmint.com/rel_uma_cinnamon.php|20.2]],[[https://linuxmint.com/rel_una_cinnamon.php|20.3]]} * fedora-{[[https://docs.fedoraproject.org/en-US/fedora/f26/release-notes/|26]],[[https://docs.fedoraproject.org/en-US/fedora/f27/release-notes/|27]],[[https://docs.fedoraproject.org/en-US/fedora/f28/release-notes/|28]],[[https://docs.fedoraproject.org/en-US/fedora/f29/release-notes/|29]],[[https://docs.fedoraproject.org/en-US/fedora/f30/release-notes/|30]],[[https://docs.fedoraproject.org/en-US/fedora/f31/release-notes/|31]],[[https://docs.fedoraproject.org/en-US/fedora/f32/release-notes/|32]],[[https://docs.fedoraproject.org/en-US/fedora/f33/release-notes/|33]],[[https://docs.fedoraproject.org/en-US/fedora/f34/release-notes/|34]],[[https://docs.fedoraproject.org/en-US/fedora/f35/release-notes/|35]],[[https://fedoraproject.org/wiki/Releases/36/ChangeSet|36]]} * centos-{7⁺,[[https://www.centos.org/centos-stream/|stream-8]],[[https://www.centos.org/centos-stream/|stream-9]]} * gentoo * archlinux * opensuse-{15,[[https://doc.opensuse.org/release-notes/x86_64/openSUSE/Leap/15.3/|15.3]],[[https://get.opensuse.org/tumbleweed/|tumbleweed]]} * slackware-14.2 * '''Linux 32-bit''' (i386/i686) * ubuntu-bionic * [[https://github.com/pypa/manylinux#manylinux_2_24-debian-9-based|manylinux-2_24]] * debian-buster * centos-7⁺ (but docbuild is broken, [[https://trac.sagemath.org/ticket/32768|#32768]]) * '''macOS (Intel)''' (x86_64) - with [[https://brew.sh/|Homebrew]] or without * macOS 10.15 (Catalina) * macOS 11.x (Big Sur) * macOS 12.x (Monterey) [[https://trac.sagemath.org/ticket/32855|#32855]] * '''macOS (Apple Silicon, M1)''' [[https://trac.sagemath.org/ticket/30592|#30592]] * Building Sage 9.5 from source on Apple Silicon (M1) requires the use of [[https://brew.sh/|Homebrew]] (recommended) or conda-forge, which package versions of `gfortran` 11 with necessary changes for this platform that are not in a released upstream version of GCC. (The `gfortran` package that comes with Sage is not suitable for the M1.) * Make sure that `/usr/local` does not contain an old copy of homebrew (or other software) for x86_64 that you may have copied from an old machine. Homebrew for the M1 is installed in `/opt/homebrew`, not `/usr/local`. * Be sure to follow the [[https://github.com/sagemath/sage/blob/develop/README.md|README]] and the instructions that the `./configure` command issues regarding the installation of system packages from Homebrew or conda. * '''Cygwin''' (x86_64) (On platforms marked with the superscript ⁺, installing optional packages is not supported in Sage 9.6; and support for these platforms will be removed in Sage 9.7; see [[https://trac.sagemath.org/ticket/32074|#32074]]. Upgrade to a newer version of the distribution or at least upgrade the toolchain (gcc, binutils).) === Help === See [[https://github.com/sagemath/sage/blob/9.4/README.md|README.md]] in the source distribution for installation instructions. |
Sage 9.6 Release Tour
Release candidate (2022)
Contents
-
Sage 9.6 Release Tour
- User interface, plotting and graphics
- Linear Algebra
- Symbolics
- Polyhedral geometry and linear programming
- Manifolds
- Algebra
- Number theory
- Coding theory
- Package upgrades
- For developers: Refactoring and modularization
-
New developer tools
- Pre-built Docker containers on ghcr.io
- Sage development in the cloud with Gitpod
- Linting workflow (pycodestyle, relint) on GitHub Actions
- Automatic incremental build for ticket branches on GitHub Actions
- Automatic documentation build for ticket branches on GitHub Actions
- Codecov
- sage --pytest
- sage -t --baseline-stats-path
- Sage patchbot on GitHub Actions
- Availability of Sage 9.6 and installation help
- More details
User interface, plotting and graphics
JupyterLab 3.3
JupyterLab, the latest web-based interactive development environment for notebooks, code, and data, is slated to replace the now-classic Jupyter notebook interface. The version of JupyterLab in the Sage distribution has been upgraded to the major new version 3.3. #32069, #33607
After ./sage -i jupyterlab_widgets, you can run it using
./sage -n jupyterlab
Also two new interface variants are provided:
./sage -n nbclassic
and
./sage -n retrolab
Interactive graph editing with phitigra
With the new optional package phitigra (use ./sage -i phitigra to install), graphs can be edited by interactively placing vertices, edges, etc. This works both in the classic Jupyter notebook and in JupyterLab.
Hyperbolic plots
Added the ability to choose the hyperbolic model for hyperbolic plots. #22081
Graphics with TikZ
The TikzPicture module which was developed in the slabbe package for more than 5 years is now in Sage. This was done in ticket #20343. Below are some usage examples.
First example shows that it takes any tikz picture string as input:
sage: from sage.misc.latex_standalone import TikzPicture
sage: s = '\\begin{tikzpicture}\n\\draw[->,green,very thick](0,0) -- (1,1);\\end{tikzpicture}'
sage: t = TikzPicture(s)
sage: t # in Jupyter, rich representation will show the image instead
\documentclass[tikz]{standalone}
\begin{document}
\begin{tikzpicture}
\draw[->,green,very thick](0,0) -- (1,1);\end{tikzpicture}
\end{document}
sage: path_to_file = t.pdf() # and opens the image in a viewer
Of course, conversion to pdf format necessitates pdflatex or lualatex. If lualatex is available it uses it in preference to pdflatex because it handles better the very big pictures in terms of memory limits.
One can provide a local filename to save to, or convert the image to other formats (using pdftocairo or imagemagick external packages):
sage: path_to_file = t.pdf('file.pdf') # when providing a filename, it just saves the file locally, does not open in a viewer
sage: path_to_file = t.png() # conversion to png
sage: path_to_file = t.svg() # to svg
sage: path_to_file = t.tex() # print the tex source to a fileAnother example with graphs where additional usepackage are necessary to compile the image correctly:
sage: from sage.misc.latex_standalone import TikzPicture
sage: g = graphs.PetersenGraph()
sage: t = TikzPicture(latex(g), standalone_config=["border=4mm"], usepackage=['tkz-graph'])
sage: t # in Jupyter, rich representation will show the image instead
\documentclass[tikz]{standalone}
\standaloneconfig{border=4mm}
\usepackage{tkz-graph}
\begin{document}
\begin{tikzpicture}
\definecolor{cv0}{rgb}{0.0,0.0,0.0}
\definecolor{cfv0}{rgb}{1.0,1.0,1.0}
\definecolor{clv0}{rgb}{0.0,0.0,0.0}
\definecolor{cv1}{rgb}{0.0,0.0,0.0}
---
65 lines not printed (3695 characters in total).
Use print to see the full content.
---
\Edge[lw=0.1cm,style={color=cv6v8,},](v6)(v8)
\Edge[lw=0.1cm,style={color=cv6v9,},](v6)(v9)
\Edge[lw=0.1cm,style={color=cv7v9,},](v7)(v9)
%
\end{tikzpicture}
\end{document}
sage: _ = t.pdf() # or t.png() or t.svg()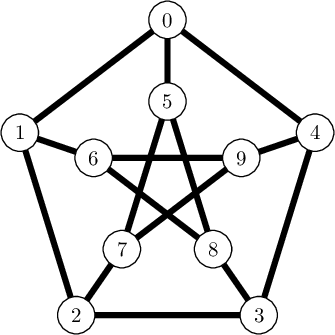
sage: from sage.misc.latex_standalone import TikzPicture sage: V = [[1,0,1],[1,0,0],[1,1,0],[0,0,-1],[0,1,0],[-1,0,0],[0,1,1],[0,0,1],[0,-1,0]] sage: P = Polyhedron(vertices=V).polar() sage: s = P.projection().tikz([674,108,-731],112) sage: t = TikzPicture(s) sage: _ = t.pdf() # or t.png() or t.svg()

The module also contains a class Standalone, from which the class TikzPicture inherits:
sage: from sage.misc.latex_standalone import Standalone
sage: s = Standalone('Hello World', usepackage=['amsmath'], standalone_config=['beamer=true','border=1mm'])
sage: s # in Jupyter, rich representation will show the image instead
\documentclass{standalone}
\standaloneconfig{beamer=true}
\standaloneconfig{border=1mm}
\usepackage{amsmath}
\begin{document}
Hello World
\end{document}
sage: _ = s.pdf() # or s.png() or s.svg()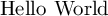
Another example using Standalone with a tableau:
sage: P = Permutations(10)
sage: p = P.random_element()
sage: p
[3, 10, 1, 9, 5, 6, 7, 2, 8, 4]
sage: t = p.to_tableau_by_shape([3,3,3,1])
sage: t
[[2, 8, 4], [5, 6, 7], [10, 1, 9], [3]]
sage: s = Standalone(latex(t), standalone_config=["border=1mm"])
sage: s
\documentclass{standalone}
\standaloneconfig{border=1mm}
\begin{document}
{\def\lr#1{\multicolumn{1}{|@{\hspace{.6ex}}c@{\hspace{.6ex}}|}{\raisebox{-.3ex}{$#1$}} }
\raisebox{-.6ex}{$\begin{array}[b]{*{3}c}\cline{1-3}
\lr{2}&\lr{8}&\lr{4}\\\cline{1-3}
\lr{5}&\lr{6}&\lr{7}\\\cline{1-3}
\lr{10}&\lr{1}&\lr{9}\\\cline{1-3}
\lr{3}\\\cline{1-1}
\end{array}$}
}
\end{document}
sage: _ = s.pdf() # or s.png() or s.svg()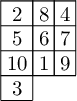
In a next step, a method tikz() will be added to graphs, polytopes, posets, etc. to return an object of type TikzPicture see #33002.
Complex plots
The complex plotting package phase_mag_plot has been incorporated into Sage. Now complex_plot allows contouring, tiling, and matplotlib-compatible colormaps. This was added in ticket #33416.
To use a colormap, one can pass in a string as in
sage: complex_plot((x - 5)*sqrt(x), (-10, 10), (-10, 10), cmap='twilight')
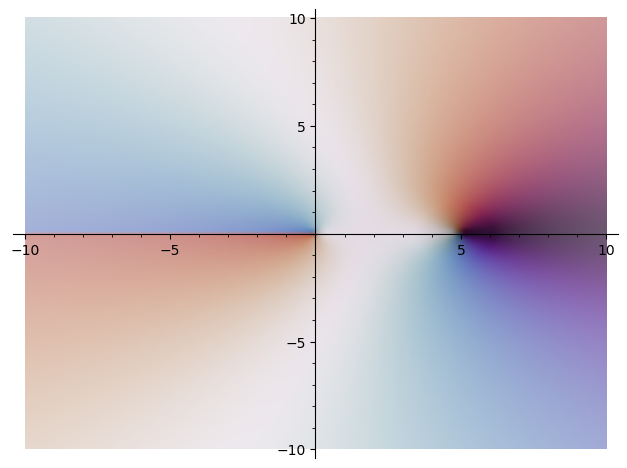
Contouring or tiling are enabled through keyword options. To look smooth, it's typically necessary to plot the function on additional points through the use of plot_points. This looks like
sage: complex_plot((x - 5)*sqrt(x), (-10, 10), (-10, 10), cmap='twilight', plot_points=500, contoured=True)
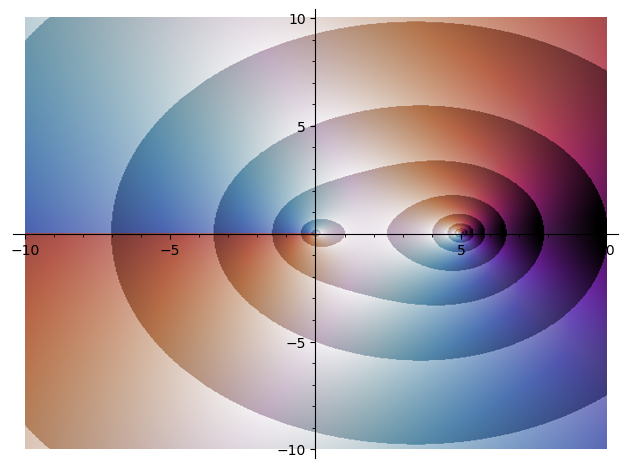
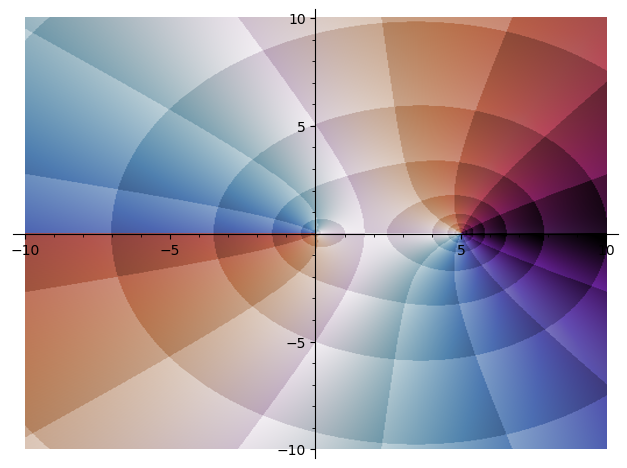
sage: complex_plot((x - 5)*sqrt(x), (-10, 10), (-10, 10), cmap='twilight', plot_points=500, tiled=True)
LaTeX displays in JupyterLab
Users of Sage in JupyterLab got used to expressions displayed at center in the LaTeX display mode. For compatibility with displays in classic Jupyter, we decided to change the behavior so that now expressions are displayed aligned left by default.
If you belong to the minority preferring centered displays, you can set your preference by
dm = get_display_manager() dm.preferences.align_latex = 'center' # or 'left'
in the ~/.sage/init.sage script.
Other improvements
Linear Algebra
NumPy integration
The new classes Matrix_numpy_integer_dense and Vector_numpy_integer_dense implement matrices and vectors with 64-bit integer entries backed by numpy arrays. #32465.
As a first application, several methods of GenericGraph that return matrices, such as adjacency_matrix, now accept keyword arguments that can select the matrix implementation. #33377, #33387, #33388, #33389
sage: graphs.PathGraph(5).adjacency_matrix(sparse=False, implementation='numpy') [0 1 0 0 0] [1 0 1 0 0] [0 1 0 1 0] [0 0 1 0 1] [0 0 0 1 0] sage: type(_) <class 'sage.matrix.matrix_numpy_integer_dense.Matrix_numpy_integer_dense'>
CombinatorialFreeModule improvements
Performing sums and similar constructions for CombinatorialFreeModule have been made faster. #33267
Symbolics
SymPy 1.10.1
SymPy has been upgraded to version 1.10.1 (release notes). #33398, #33547, #33584
ImageSet
Sage 9.6 defines a new class ImageSet. #32121
sage: ImageSet(sin, RealSet.open(0, pi/4))
Image of (0, 1/4*pi) by The map sin from (0, 1/4*pi)
sage: _.an_element()
1/2*sqrt(-sqrt(2) + 2)
sage: sos(x,y) = x^2 + y^2; sos
(x, y) |--> x^2 + y^2
sage: ImageSet(sos, ZZ^2)
Image of
Ambient free module of rank 2 over the principal ideal domain Integer Ring by
The map (x, y) |--> x^2 + y^2 from Vector space of dimension 2 over Symbolic Ring
sage: _.an_element()
1
sage: ImageSet(sos, Set([(3, 4), (3, -4)]))
Image of {...(3, -4)...} by
The map (x, y) |--> x^2 + y^2 from Vector space of dimension 2 over Symbolic Ring
sage: _.an_element()
25The new class mirrors and translates to SymPy's ImageSet:
sage: from sage.sets.image_set import ImageSet sage: S = ImageSet(sin, RealSet.open(0, pi/4)); S Image of (0, 1/4*pi) by The map sin from (0, 1/4*pi) sage: S._sympy_() ImageSet(Lambda(x, sin(x)), Interval.open(0, pi/4))
Most methods of ImageSet are actually provided by its base class, the new class ImageSubobject. For all morphisms in the Sets category, there is now a default method image, which constructs an instance of either ImageSubobject or ImageSet.
Orthogonal polynomials
Three classes of classical (discrete) orthogonal polynomials in the Askey scheme have been added: #33393
- Krawtchouk polynomials
- Hahn polynomials
- Meixner polynomials
Polyhedral geometry and linear programming
polymake 4.6
polymake, a comprehensive system for computations in polyhedral geometry, tropical geometry, etc., has been upgraded to version 4.6 (release notes). #33251
CyLP
The new optional package CyLP (./sage -i cylp) provides a detailed interface to Clp, the COIN-OR linear programming solver, and Cbc, the COIN-OR branch-and-cut solver for mixed-integer linear programs. #33847
In a future version of Sage, CyLP is intended to provide a replacement for the Sage-specific backend interface to Clp and Cbc, sage-numerical-backends-coin; see Meta-ticket #26511.
Equivariant Ehrhart theory
Manifolds
Improved Manifold constructor
The structure parameter of the Manifold constructor has new, more convenient defaulting behavior. #33001
When parameters such as diff_degree or metric_name are given, the implied structure is selected:
sage: M = Manifold(3, 'M', diff_degree=0); M 3-dimensional topological manifold M sage: M = Manifold(3, 'M', diff_degree=2); M 3-dimensional differentiable manifold M sage: M = Manifold(3, 'M', metric_name='g'); M 3-dimensional Riemannian manifold M
Symplectic manifolds
Symplectic structures have been added to Sage (#30362).
Projective spaces
Real projective spaces have been added to the manifold catalog (#33221). For example, one can construct the real projective plane.
sage: RP2 = manifolds.RealProjectiveSpace(); RP2
2-dimensional topological manifold RP2
sage: latex(RP2)
\mathbb{RP}^{2}There are three charts. Considering an immersion in three-dimensional Euclidean space, the chart corresponds to a choice of one (out of three possible) coordinates to be always nonzero. The coordinates listed are the two other coordinates assuming that the nonzero coordinate is always one.
sage: C0, C1, C2 = RP2.top_charts()
sage: p = RP2.point((2,0), chart = C0)
sage: q = RP2.point((0,3), chart = C0)
sage: p in C0.domain()
True
sage: p in C1.domain()
True
sage: C1(p)
(1/2, 0)
sage: p in C2.domain()
False
sage: q in C0.domain()
TrueThe point q looks like (1,0,3) in ambient Euclidean space, so it is not in the domain of the chart C1. It also has the form (1/3,0,1) when considered in the chart C2.
sage: q in C1.domain()
False
sage: q in C2.domain()
True
sage: C2(q)
(1/3, 0)If both coordinates in a local chart are nonzero then that point is in the domain of all charts. The change of coordinates is found by normalizing the appropriate chart. So for example, the point (1, 2, 3) is the same as the point (1/2, 1, 3/2) is the same as the point (1/3, 2/3, 1), which is reflected by defining r to be a point in the default chart C0.
sage: r = RP2.point((2,3))
sage: r in C0.domain() and r in C1.domain() and r in C2.domain()
True
sage: C0(r) # corresponding to (1, 2, 3)
(2, 3)
sage: C1(r) # corresponding to (1/2, 1, 3/2)
(1/2, 3/2)
sage: C2(r) # corresponding to (1/3, 2/3, 1)
(1/3, 2/3)
Algebra
lrcalc 2.1
lrcalc, Anders Buch's Littlewood-Richardson Calculator, has been upgraded to the major new version 2.1 changelog. #31355
Finitely presented modules over graded algebras
Sage 9.6 allows the construction of finitely presented modules over graded algebras, even algebras which are infinite and/or noncommutative like the mod p Steenrod algebra. Some homological algebra is implemented in general, and more tools are implemented specifically for modules over the Steenrod algebra (#32505, #30680).
sage: from sage.modules.fp_graded.module import FPModule
sage: E.<x,y> = ExteriorAlgebra(QQ)
# M has one generator g in degree 0 and two relations, x*g and y*g.
# That is, M is QQ as a trivial E-module.
sage: M = FPModule(E, [0], [[x], [y]])
# Free resolution:
sage: M.resolution(3)
[Module morphism:
From: Free graded left module on 1 generator over
The exterior algebra of rank 2 over Rational Field
To: Finitely presented left module on 1 generator and 2 relations over
The exterior algebra of rank 2 over Rational Field
Defn: g[0] |--> g[0],
Module morphism:
From: Free graded left module on 2 generators over
The exterior algebra of rank 2 over Rational Field
To: Free graded left module on 1 generator over
The exterior algebra of rank 2 over Rational Field
Defn: g[1, 0] |--> x*g[0]
g[1, 1] |--> y*g[0],
Module morphism:
From: Free graded left module on 3 generators over
The exterior algebra of rank 2 over Rational Field
To: Free graded left module on 2 generators over
The exterior algebra of rank 2 over Rational Field
Defn: g[2, 0] |--> x*g[1, 0]
g[2, 1] |--> y*g[1, 0] + x*g[1, 1]
g[2, 2] |--> y*g[1, 1],
Module morphism:
From: Free graded left module on 4 generators over
The exterior algebra of rank 2 over Rational Field
To: Free graded left module on 3 generators over
The exterior algebra of rank 2 over Rational Field
Defn: g[3, 0] |--> x*g[2, 0]
g[3, 1] |--> y*g[2, 0] + x*g[2, 1]
g[3, 2] |--> y*g[2, 1] + x*g[2, 2]
g[3, 3] |--> y*g[2, 2]]There is a new thematic tutorial providing many details and examples.
Miscellaneous improvements
Ideal membership over quotient rings can now be decided (by reducing to ideal membership in the parent ring). #33237
Iterating over (some) infinite modules (including ℤ^n) now enumerates the entire module, in a "natural" order. #33287
BinaryQF.solve_integer() now also works for quadratic forms of square discriminant. #33026
Quaternion fractional ideals (including orders) now support the usual operations (e.g., a*I, I*a, I+J). #32264
AdditiveAbelianGroupWrapper now exposes .discrete_log() for (multi-dimensional) logarithms in finite abelian groups. #32384
Graded submodules of graded modules now know they are graded (with respect to the ambient grading); similarly for filtered submodules. #33321
Polynomials now evaluate faster on monomial inputs. #33165
Implement specialized code for summing terms and monomials in CombinatorialFreeModule. #33267
Improvements and fixes to skew_by() in symmetric functions. #33313
Attempt to invert elements generically in a finite dimensional algebra. #33250
Tensor products of finite dimensional modules know they are finite dimensional (Sage does not currently have any structure for infinite tensor products, which can have some subtleties). #30252
Improved coercions and conversions with Laurent polynomials and their fraction field. #31320 #33477
Faster evaluation of univariate polynomials with monomials. #33165
Number theory
Elliptic curves
Elliptic-curve DLP and Weil pairings over finite fields are now much faster (thanks to PARI). #33121
Scalar multiplication on elliptic curves over finite fields is now significantly faster (thanks to PARI). #33147
Computing the Weierstraß ℘ function of an elliptic curve is now significantly faster (thanks to PARI). #33223
Classes used by the Monsky-Washnitzer curves now use the new coercion system. #33525 #33576
Coding theory
Optimizations to SBox. #25633
Package upgrades
For a list of all packages and their versions, see
Python 3.10
Sage 9.6 continues to support system Python 3.7.x to 3.10.x. If no suitable version of Python is installed in the system, Sage will install its own copy of Python. Sage now ships Python 3.10.3 for this purpose. #30767, #33512
FLINT 2.8.x and arb 2.22.x
FLINT has been upgraded from 2.7.1 to 2.8.4.#32211
The FLINT 2.8 series brings major new algorithms and general speedups (release notes).
Note that Sage accepts system installations of FLINT >= 2.6.x. Users on older distributions who want to benefit from the speed ups in FLINT 2.8.x may want to use ./configure --without-system-flint.
Meta-ticket #31408 tracks the effort to make use of new features added in recent FLINT releases in the Sage library.
arb has been upgraded from 2.19.0 to 2.22.1. #32211, #33189
The 2.20, 2.21, and 2.22 series have brought major new algorithms and other improvements (changelog).
igraph 0.9.x
The igraph library and its Python interface (now also just called igraph) have been upgraded to versions 0.9.7/0.9.9. #32510, #33526
For developers: Refactoring and modularization
See also Meta-ticket #29705
sage.features.Executable.absolute_filename()
The Sage library interfaces to some external non-Python packages by running an executable program in a separate process. The package may either be available from a system installation, or the Sage distribution may have installed the package in the SAGE_LOCAL prefix hierarchy. The main sage script sets up various environment variables before starting the Python interpreter; in particular, it sets PATH to include SAGE_LOCAL/bin, which ensures that the installed executables are found.
In Sage 9.6, we have changed most calls to executables so that they no longer depend on the environment variable PATH being set in this way. Every executable program is represented by an instance of sage.features.Executable. Its method absolute_filename explicitly searches inside SAGE_LOCAL/bin (in installations with SAGE_LOCAL) before it depends on PATH. #31292, #31296, #32645, #32893, #33440, #33465, #33467
Preparations for PEP 420 implicit namespace packages
The Sage doctester is now prepared for namespace packages. #33033
To reduce runtime dependencies, many imports from sage.graphs.all, sage.interfaces.all, sage.misc.all, sage.libs.all, sage.rings.all have been replaced by more specific imports; and module-level imports from sage.plot have been changed to either use lazy_import or have been moved inside methods. #30582, #32847, #32989, #32999, #33000, #33007, #33146, #33199, #33466, #33468
Lazy imports of classes now support __instancecheck__ and __subclasscheck__
No Python object is an instance of a class that cannot be imported from the module that defines it. The new special method LazyImport.__instancecheck__ now just returns False in this case. #33017
This provides a convenient pattern for writing modularized code when creating an abstract base class for "isinstance" testing is not justified.
sage: from sage.schemes.generic.scheme import Scheme
sage: sZZ = Scheme(ZZ)
sage: lazy_import('xxxx_does_not_exist', 'Pluffe')
sage: isinstance(sZZ, (Scheme, Pluffe))
True
sage: isinstance(ZZ, (Scheme, Pluffe))
FalseLikewise, no class is a subclass of a class that cannot be imported from the module that defines it; so the new special method LazyImport.__subclasscheck__ implements the same logic.
sage.geometry.polyhedron.base reorganized
The module sage.geometry.polyhedron.base has been split into several modules, grouping the methods of class Polyhedron_base according to their topic and runtime dependencies on other parts of Sage. #32651
New developer tools
Pre-built Docker containers on ghcr.io
Our portability CI on GitHub Actions builds Docker images for all tested Linux platforms (and system package configurations) and makes them available on GitHub Packages (ghcr.io). #39033
Since 9.6.beta1, the image version corresponding to the latest development release receives the additional Docker tag dev, see for example the Docker image for ubuntu-impish-standard. Thus, for example, the following command will work:
$ docker run -it ghcr.io/sagemath/sage/sage-docker-ubuntu-impish-standard-with-targets-optional:dev bash
Images whose names end with the suffix -with-targets-optional are the results of full builds and a run of make ptest. They also contain a copy of the source tree and the full logs of the build and test.
Smaller images corresponding to earlier build stages are also available:
-with-system-packages provides a system installation with system packages installed, no source tree,
-configured contains a partial source tree and has completed bootstrap and the configure,
-with-targets-pre contains the full source tree and a full installation of all non-Python packages,
-with-targets contains the full source tree and a full installation of Sage, including the HTML documentation, but make ptest has not been run yet.
Sage development in the cloud with Gitpod
Gitpod is a service that provides a development environment in the cloud based on VS Code. It is free to use for up to 50 hours per month. Sage now includes a configuration for Gitpod; see the new section Setting up your workspace in the Sage Developer's Guide. #33103, #33589
To launch Gitpod on a branch of a Trac ticket, you can use the new Gitpod badge in the ticket box.
Linting workflow (pycodestyle, relint) on GitHub Actions
A linting workflow on GitHub Actions runs on all pushes to a branch on Trac. It checks that the code of the current branch adheres to the style guidelines using pycodestyle (in the pycodestyle-minimal configuration) and relint.
In order to see details when it fails, you can click on the badge and then select the most recent workflow run.
Sage 9.6 includes again many improvements to the coding style checked by pycodestyle. #32978, #32979, #33095, #33102, ...
Consequently, the pycodestyle-minimal configuration has been extended to enforce E111, E401, E701, E702, E703, W605, E711, E712, E713, E721, E722.
Automatic incremental build for ticket branches on GitHub Actions
The build & test workflow on GitHub Actions builds Sage for the current branch (incrementally on top of the system packages of the develop branch) and runs the test.
Details are again available by clicking on the badge.
Note that in contrast to the patchbot, the ticket branch is not merged into the current beta version.
Automatic documentation build for ticket branches on GitHub Actions
The build documentation workflow on GitHub Actions builds the HTML documentation for the current branch.
If you click on the badge, you get the HTML output of the successful run. The idea is to use this to easily inspect changes to the documentation without the need to locally rebuild the docs yourself. If the doc build fails, you can go to the Actions tab of sagemath/sagetrac-mirror repo and choose the particular branch to see what went wrong.
The idea is that these three status badges complement the existing patchbots (and maybe even replace them in the future). In particular, they are supposed to always be green.
Codecov
sage --pytest
After the optional package pytest is installed (./sage -i pytest), a new command ./sage --pytest is available, which runs pytest on the Sage library sources. #33572
Also the Sage doctester (./sage -t or ./sage -tox -e doctest) invokes pytest. This functionality has been improved in Sage 9.6. #31924, #32975
sage -t --baseline-stats-path
Sage patchbot on GitHub Actions
The Sage patchbot can now be run on GitHub Actions, on top of any of the Linux platforms for which we have prebuilt Docker images.#33253
Availability of Sage 9.6 and installation help
The first development release of the 9.6 series, 9.6.beta0, was tagged on 2022-02-06. The first release candidate, 9.6.rc0, was tagged on 2022-04-10.
The SageMath installation guide now provides a decision tree that guides users and developers to a type of installation suitable for their system and their needs.
Sources
The Sage source code is available in the sage git repository.
SageMath 9.6 supports all platforms that were supported by Sage 9.5 and adds support for building on distributions that use the (unreleased) GCC 12 series (fedora-36). #33187
Linux 64-bit (x86_64)
Linux 32-bit (i386/i686)
- ubuntu-bionic
- debian-buster
centos-7⁺ (but docbuild is broken, #32768)
macOS (Intel) (x86_64) - with Homebrew or without
- macOS 10.15 (Catalina)
- macOS 11.x (Big Sur)
macOS 12.x (Monterey) #32855
macOS (Apple Silicon, M1) #30592
Building Sage 9.5 from source on Apple Silicon (M1) requires the use of Homebrew (recommended) or conda-forge, which package versions of gfortran 11 with necessary changes for this platform that are not in a released upstream version of GCC. (The gfortran package that comes with Sage is not suitable for the M1.)
Make sure that /usr/local does not contain an old copy of homebrew (or other software) for x86_64 that you may have copied from an old machine. Homebrew for the M1 is installed in /opt/homebrew, not /usr/local.
Be sure to follow the README and the instructions that the ./configure command issues regarding the installation of system packages from Homebrew or conda.
Cygwin (x86_64)
(On platforms marked with the superscript ⁺, installing optional packages is not supported in Sage 9.6; and support for these platforms will be removed in Sage 9.7; see #32074. Upgrade to a newer version of the distribution or at least upgrade the toolchain (gcc, binutils).)
Help
See README.md in the source distribution for installation instructions.
See sage-devel for development discussions and sage-release for announcements of beta versions and release candidates.
