Sage 2.11 Release Tour
Sage 2.11 was released on March 30, 2008. For the official, comprehensive release notes, see the HISTORY.txt file that comes with the release. For the latest changes see sage-2.11.txt.
ATLAS
Michael Abshoff and Burcin Erocal upgraded ATLAS to the 3.8.1 release. In addition tuning info for 32 bit Prescott CPUs as well as Powerbook G4s under Linux was added.
zn_poly
David Harvey's zn_poly library is now a standard package for Sage. zn_poly is a new C library for polynomial arithmetic in (Z/nZ)[x] where 3 \le n \le ULONG\_MAX (i.e. any machine-word-sized modulus). The main benefit is speed. Three examples on sage.math, from my current development code (this code is not yet in the spkg):
Multiplying length 200 polynomials over Z/nZ where n has 10 bits:
- NTL (zz_pX): 113 µs
- Magma: 44 µs
zn_poly: 13 µs
Multiplying length 10^6 polynomials over Z/nZ where n has 40 bits and is odd:
- NTL (zz_pX): 9.1s
- Magma: 8.3s
zn_poly: 2.06s
Reciprocal of a length 10^6 power series over Z/nZ where n has 40 bits and is odd:
- NTL (zz_pX): 25.4s
- Magma: ludicrously slow, maybe I'm doing something wrong
zn_poly: 3.62s
The library is used so far only to compute the zeta function for hyperelliptic curves.
small roots method for polynomials mod N (N composite)
Coppersmith's method for finding small roots of univariate polynomials modulo N where N is composite was implemented. An application of this method is to consider RSA. We are using 512-bit RSA with public exponent e=3 to encrypt a 56-bit DES key. Because it would be easy to attack this setting if no padding was used we pad the key K with 1s to get a large number.
We choose two primes of size 256-bit each.
We choose a random key
1 sage: K = ZZ.random_element(0, 2^Kbits)
and pad it with 512-56=456 1s
Now we encrypt the resulting message:
1 sage: C = ZmodN(M)^e
To recover K we consider the following polynomial modulo N:
and recover its small roots:
Generic Multivariate Polynomial Arithmetic
Joel Mohler improved the efficiency of the generic multivariate polynomial arithmetic in Sage. Before his patch was applied:
and after:
k-Schur Functions and Non-symmetric Macdonald Polynomials
k-Schur functions s_\lambda^{(k)} are a relatively new family of symmetric functions which play a role in \mathbb{Z}[h_1, \ldots, h_k] as the Schur functions s_\lambda do in \Lambda. The k-Schur functions, amongst other things, provide a natural basis for the quantum cohomology of the Grassmannian. The k-Schur functions can be used like any other symmetric functions and are created with kSchurFunctions.
Non-symmetric Macdonald polynomials in type A can now be accessed in Sage. The polynomials are computed from the main theorem in "A Combinatorial Formula for the Non-symmetric Macdonald Polynomials" by Haglund, Haiman, and Loehr. ( http://arxiv.org/abs/math.CO/0601693 )
Improved capabilities for solving matrix equations
William Stein implemented code so that one can now solve matrix equations AX = B and XA=B whenever a solution exists. In particular, solving linear equations now works even if A is singular or nonsquare.
sage: A = matrix(QQ,2,3, [1,2,3,2,4,6]); v = vector([-1/2,-1]) sage: x = A \ v; x (-1/2, 0, 0) sage: A*x == v True
Generators for congruence subgroups
Robert Miller implemented an algorithm for very quickly computing generators for congruence subgroups \Gamma_0(N), \Gamma_1(N), and \Gamma_H(N).
sage: Gamma0(11).generators() [[1 1] [0 1], [-1 0] [ 0 -1], ... [10 -1] [11 -1], [-10 1] [-11 1]] sage: time G = Gamma0(389).generators() CPU times: user 0.03 s, sys: 0.01 s, total: 0.04 s Wall time: 0.04 sage: time G = Gamma0(997).generators() CPU times: user 0.14 s, sys: 0.00 s, total: 0.14 s Wall time: 0.14 sage: time G = Gamma0(2008).generators() CPU times: user 0.82 s, sys: 0.00 s, total: 0.82 s Wall time: 0.82 sage: len(G) 3051
gfan-0.3 upgrade, improved interface
@interact
def gfan_browse(p1 = input_box('x^3+y^2',type = str, label='polynomial 1: '), p2 = input_box('y^3+z^2',type = str, label='polynomial 2: '), p3 = input_box('z^3+x^2',type = str, label='polynomial 3: ')):
R.<x,y,z> = PolynomialRing(QQ,3)
i1 = ideal(R(p1),R(p2),R(p3))
gf1 = i1.groebner_fan()
testr = gf1.render()
html('Groebner fan of the ideal generated by: ' + str(p1) + ', ' + str(p2) + ', ' + str(p3))
show(testr, axes = False, figsize=[8,8*(3^(.5))/2])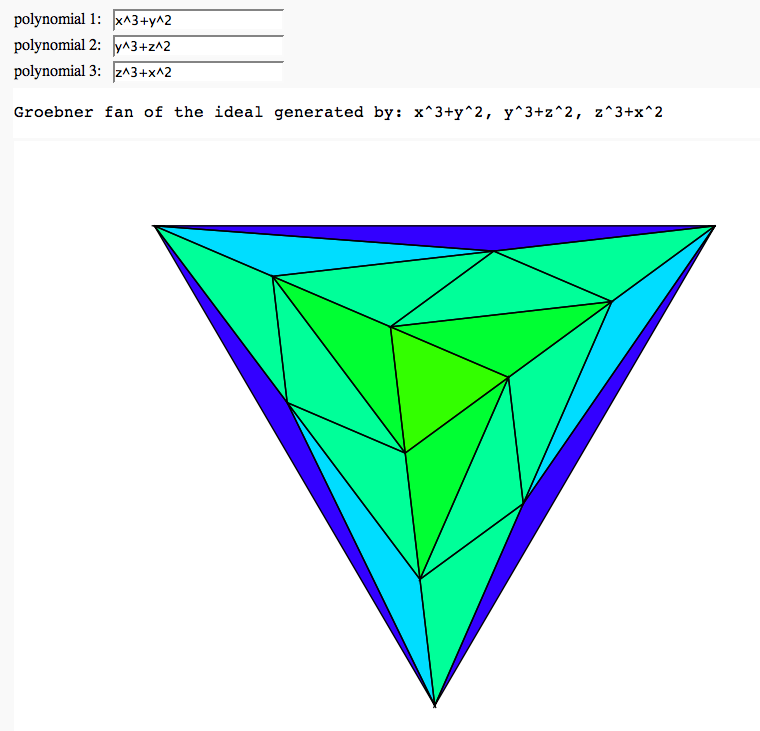
Bugfixes/Upgrades (incomplete)
- misc:
#2148 PolyBoRi monomial orders are wrong
- #2437 Update eclib.spkg to eclib-20080304
- #2468 inverting a non-invertible matrix over RDF returns weird results
- #2517 ignore bad values in plot
#2545 FractionFieldElement lacks derivative method
- #2566 fix all known bugs in graph_isom and binary_code
#2571 problem with copy() on sage.rings.integer_mod.IntegerMod_gmp
- #2574 problem with Abelian groups and trivial elements
- #2576 preserve docstrings of decorated methods in multi_polynomial_ideal.py
- #2579 Inconsistency in integer quotient
- #2581 extend solve_right to all cases; implement solve_left
#2582 fix bug in PermutationGroupElement
- #2585 padic bugfix - check=False in constructor
- #2587 subgroup of a permutation group is so slow it's silly
- #2588 documentation and tests for sage.schemes.hyperelliptic_curves.jacobian_morphism
- #2593 Sage chokes on utf-8 in .sage files
#2594 MPolynomial_polydict floordiv wrong arithmetic fixed
- #2602 plot_vector_field docs are unnecessarily complicated (and use the slow lambda functions!)
- #2584 printing bug with list_function()
