Coding Theory in Sage
A collection of ideas and long-term goals for Coding Theory in Sage, and the people interested.
Feel free to add yourself to the list below. Please elaborate on the roadmap and discussions on long-term improvements to the parts of Coding Theory in Sage that you are passionate about.
People in CT in Sage and their main interests
- jsrn: Johan Rosenkilde (DTU, Denmark). anything sage.coding, algebra
- dlucas: David Lucas
- cpernet: Clément Pernet
- danielaugot: Daniel Augot (Inria, Saclay)
You are welcome to Cc these developers on tickets related to Coding theory within their interest.
Main communication channel: sage-coding-theory Google Group
This mailing list, a little brother to sage-devel, is where we communicate:
https://groups.google.com/forum/#!forum/sage-coding-theory
Subscribe to this low-volume mailing list if you want to be kept in the loop, and write on it for any discussion on coding theory in Sage.
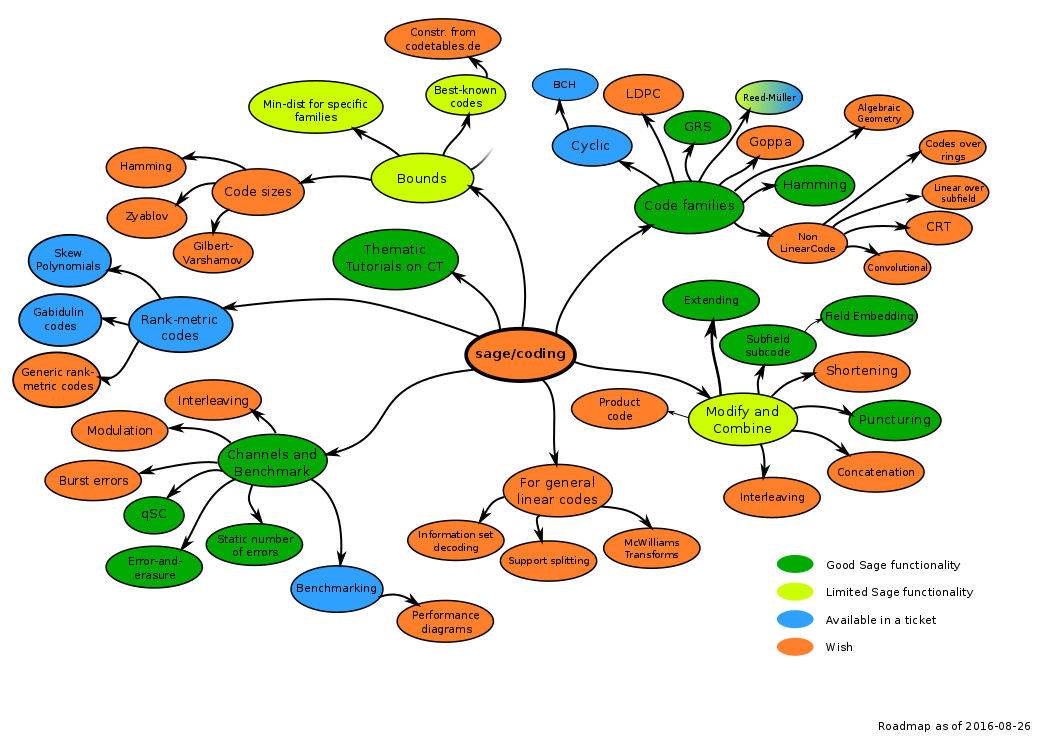
Roadmap
The following represents existing and wished Coding Theory in Sage. Please add your wishes to this diagram (and update it if it is out of date).
The diagrams are non-standard SVG created with Inkscape. The shown images are PNG rendering. Modifications should be done to the SVG.
Main Roadmap
Decoders Roadmap
Detailed discussions
A-G Codes
Support Algebraic Geometric codes in Sage rests on the following building blocks:
Representation of algebraic curves. Done: Curve and AffineSpace/ProjectiveSpace.
Representation of divisors. Done: see Curve.divisor.
- Computation of Riemann-Roch space bases. TODO.
Feel free to contact jsrn if you are interested in contributing to this.
Bounds and optimal codes
Not very easy, no support yet. What to do with http://codetables.de ?
Non-linear codes
AbstractLinearCodes supports only linear codes in the classical sense: vector spaces in F^n for some finite field F, considered over the Hamming metric. There's many relevant relaxations of this restriction.
For optimal code sharing, an hierarchy of abstract code classes should be thought out to accommodate these.
Subfield linear codes
Codes that are linear over a subfield. Examples include Interleaved linear codes, Folded RS codes and Multiplicity codes.
Relation with Guava
See Coding_Theory/Guava. The most valuable part seems to be Leon's code for computing the automorphism group of a code
Representing automorphisms of codes
Sage is reasonably good at computing automorphisms of codes with the methods automorphisms_group_gens, permutation_automorphism_group, and the related method canonical_representative. These use an efficient C implementation written by Thomas Feuler, based on his PhD thesis.
However, the representations of such automorphisms is very lacking. For instance, the "groups" returned by the above methods are simply a list of generators, with no group methods attached to them. And one cannot take an element of this group and apply it to e.g. a codeword or a whole code.
Using a nice, Sage-wide algebraic representation would also make it much easier to implement the automorphism groups of special families for which it is known, e.g. Reed-Solomon codes.
In sage.schemes there has been some recent development in automorphism groups of curves. Perhaps this can serve as a base?
General algebra in Sage that is important for coding theory
- Link to advanced fast polynomial arithmetic library functions such as multi-point evaluation and Lagrange interpolation.
- Link to fast GF(2)[x] library (currently used is NTL generic GF(p)[x]).
Port implementation of asymptotically fast (GF(q)[x])[y] root-finding from Codinglib: Ticket http://trac.sagemath.org/ticket/21333 (needing review).
Fix and review http://trac.sagemath.org/ticket/16742 regarding faster F[x] matrix reduction.
Various Other Projects
- Implement the Hartmann-Tzeng bound for cyclic codes. See =20100 for cyclic codes.
- Cython implementation of the Brouwer-Zimmermann algorithm for computing the minimum distance of a linear code.
Create a proper code class for any construction in code_constructions.py, and endow it with (some of) the known properties for that class.
- Implement a class for Goppa codes. Implement a decoder, e.g. based on its formulation as a subfield subcode of a GRS code.
Create a class for binary codes and move the binary-code specific methods of AbstractLinearCode into this class. Possibly think the efficient binary code methods in sage.coding.binary_code.pyx into it.
- Create a class for two-weight codes. Rewrite sage.coding.two_weight_db.py such that it creates elements of this class.
- Create a class for self-dual codes. Think sage.coding.sd_codes into it.
- Create a base class for codes over (ZZ mod N). See =6452 for the relevant base module structure. Create a class for the famous Z4 codes and their embedding into binary codes.
A bit a history : ACTIS, bootstrapping Coding Theory in Sage
Johan Rosenkilde, Clément Pernet and Daniel Augot got INRIA funding for a 2 years project, ACTIS ("Algorithmic Coding Theory in Sage), 2014-2016, and David Lucas (dlucas) was hired to (re)develop coding theory functionality for Sage, with a strong bias towards algebraic codes and their associated decoding algorithms.
We are in the immediate post-phase of this project, which is now finished. Yet there are some issues that we pointed out on the (deprecated) ACTIS Bitbucket issue tracker which need to be moved to trac.