|
Size: 2477
Comment:
|
Size: 2532
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 13: | Line 13: |
| r2 = x^2 + y^2 | r2 = x**2 + y**2 |
| Line 16: | Line 16: |
| integrando = (x*yp -y*xp)/r2 | integrando = (x*yp -y*xp) / r2 |
| Line 18: | Line 18: |
| return round(i/(2*pi)) | return round(i / (2 * pi)) |
| Line 24: | Line 24: |
| delta= (b-a)/N | delta = (b - a) / N |
| Line 26: | Line 26: |
| for t in srange(a, b ,delta): | for t in srange(a, b, delta): |
| Line 28: | Line 28: |
| zeros.append(find_root(f, t-epsilon, t+delta+epsilon)) | zeros.append(find_root(f, t - epsilon, t + delta + epsilon)) |
| Line 32: | Line 32: |
| if not zeros: return zeros if abs(zeros[0] + 2*pi - zeros[-1])<epsilon: |
if not zeros: return zeros if abs(zeros[0] + 2*pi - zeros[-1]) < epsilon: |
| Line 37: | Line 38: |
| if abs(c - zeros_cleaned[-1])>epsilon: | if abs(c - zeros_cleaned[-1]) > epsilon: |
| Line 39: | Line 40: |
| if abs(zeros[0] + 2*pi - zeros[-1])<epsilon: | if abs(zeros[0] + 2*pi - zeros[-1]) < epsilon: |
| Line 46: | Line 47: |
| x = x.function(t); y = y.function(t); | x = x.function(t) y = y.function(t) |
| Line 55: | Line 57: |
| html(r'$\int \frac{1}{x^2 + y^2}(xdy-ydx)=%d$'%winding_number_integral(x,y,a,b)) | pretty_print(r'$\int \frac{1}{x^2 + y^2}(xdy-ydx)=%d$'%winding_number_integral(x,y,a,b)) |
| Line 57: | Line 59: |
| zeros = all_the_zeros(x,a, b) | zeros = all_the_zeros(x, a, b) |
| Line 70: | Line 72: |
| print('Winding number = (# of red points) - (# of green points): {}'.format(wn)) | print('Winding number = (number of red points) - (number of green points): {}'.format(wn)) |
Sage Interactions - Topology
goto interact main page
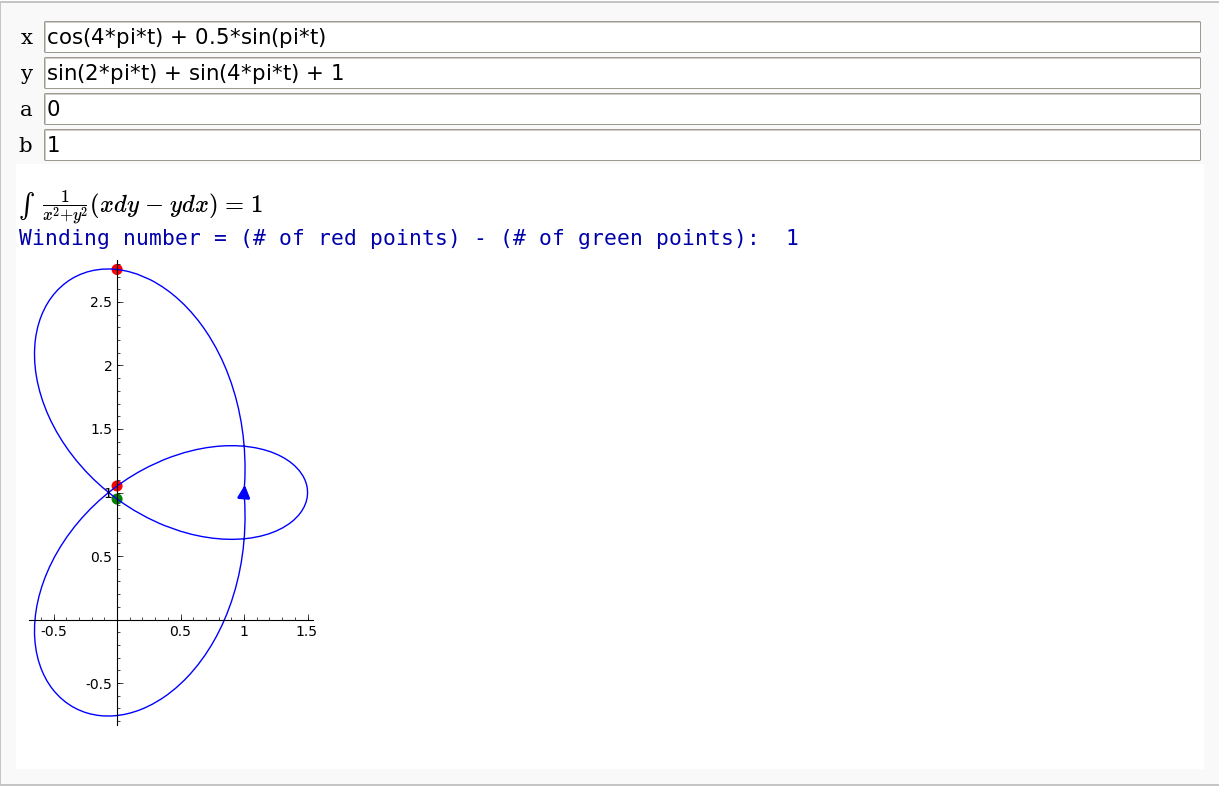
Winding number of a plane curve
by Pablo Angulo. Computes winding number (with respect to the origin!) as an integral, and also as a intersection number with a half line through the origin.