Differences between revisions 2 and 3
⇤ ← Revision 2 as of 2011-03-15 14:48:12 →
Size: 2457
Editor: pang
Comment: detail: show the origin
← Revision 3 as of 2012-04-18 18:41:31 → ⇥
Size: 2467
Editor: bvarberg
Comment:
Deletions are marked like this. Additions are marked like this.
Line 9: Line 9:
{{{ {{{#!sagecell

Sage Interactions - Topology

goto interact main page

Contents

  1. Sage Interactions - Topology
    1. Winding number of a plane curve

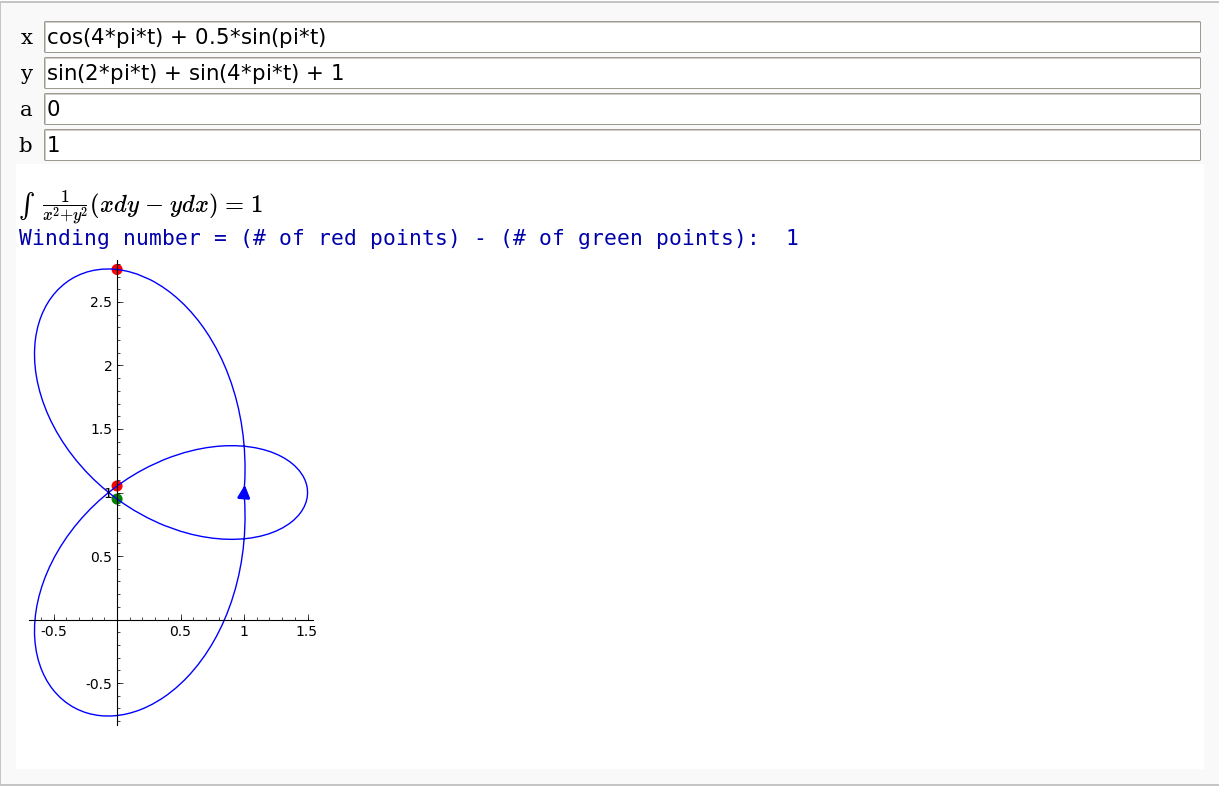
Winding number of a plane curve

by Pablo Angulo. Computes winding number (with respect to the origin!) as an integral, and also as a intersection number with a half line through the origin.

winding.png

interact/topology (last edited 2020-06-01 18:42:11 by kcrisman)