|
Size: 34981
Comment:
|
Size: 48538
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 79: | Line 79: |
| html(s) | pretty_print(html(s)) |
| Line 89: | Line 89: |
| html("<font color='red'>$\pi(x)$</font> and <font color='blue'>$x/(\log(x)-1)$</font> for $x < %s$"%N) | pretty_print(html("<font color='red'>$\pi(x)$</font> and <font color='blue'>$x/(\log(x)-1)$</font> for $x < %s$"%N)) |
| Line 115: | Line 115: |
| else: print 'NaN' | else: print('NaN') |
| Line 140: | Line 140: |
| if start < 1 or end <=start: print "invalid start or end value" if n > end: print "WARNING: n is larger than the end value" |
if start < 1 or end <=start: print("invalid start or end value") if n > end: print("WARNING: n is larger than the end value") |
| Line 172: | Line 172: |
| #print x_cord, y_cord | |
| Line 183: | Line 182: |
| #print x, "=x y=", y, " num =", num | |
| Line 209: | Line 207: |
| print '(to go from x,y coords to an n, reset by setting n=0)' | print('(to go from x,y coords to an n, reset by setting n=0)') |
| Line 211: | Line 209: |
| #print 'if n =', n, 'then (x,y) =', (x_cord, y_cord) print '(x,y) =', (x_cord, y_cord), '<=> n =', find_n(x_cord, y_cord, start) print ' ' print "SW/NE line" if -y_cord<x_cord: print '4*t^2 + 2*t +', -x_cord+y_cord+start else: print '4*t^2 + 2*t +', +x_cord-y_cord+start print "NW/SE line" if x_cord<y_cord: print '4*t^2 +', -x_cord-y_cord+start else: print '4*t^2 + 4*t +', +x_cord+y_cord+start |
print('(x,y) =', (x_cord, y_cord), '<=> n =', find_n(x_cord, y_cord, start)) print(' ') print("SW/NE line") if -y_cord<x_cord: print('4*t^2 + 2*t +', -x_cord+y_cord+start) else: print('4*t^2 + 2*t +', +x_cord-y_cord+start) print("NW/SE line") if x_cord<y_cord: print('4*t^2 +', -x_cord-y_cord+start) else: print('4*t^2 + 4*t +', +x_cord+y_cord+start) |
| Line 233: | Line 230: |
Needs fix for show_factors |
|
| Line 239: | Line 238: |
| if start < 1 or end <=start: print "invalid start or end value" if n > end: print "WARNING: n is greater than end value" |
if start < 1 or end <=start: print("invalid start or end value") if n > end: print("WARNING: n is greater than end value") |
| Line 262: | Line 261: |
| print 'n =', factor(n) | print('n = {}'.format(factor(n))) |
| Line 284: | Line 283: |
| print 'Pink Curve: n^2 +', c print 'Green Curve: n^2 + n +', c2 |
print('Pink Curve: n^2 +', c) print('Green Curve: n^2 + n +', c2) |
| Line 312: | Line 311: |
| print M; print '\n'*3 print "Computing basis...\n\n" |
print(M) print('\n' * 3) print("Computing basis...\n\n") |
| Line 315: | Line 315: |
| print "Space has dimension 0" | print("Space has dimension 0") |
| Line 317: | Line 317: |
| prec = max(prec, M.dimension()+1) | prec = max(prec, M.dimension() + 1) |
| Line 320: | Line 320: |
| print "\n\n\nDone computing basis." | print("\n\n\nDone computing basis.") |
| Line 328: | Line 328: |
| {{{#!sagecell html('<h1>Cuspidal Subgroups of Modular Jacobians J0(N)</h1>') |
ncols not working {{{#!sagecell pretty_print(html('<h1>Cuspidal Subgroups of Modular Jacobians J0(N)</h1>')) |
| Line 333: | Line 335: |
| print A.cuspidal_subgroup() | print(A.cuspidal_subgroup()) |
| Line 475: | Line 477: |
| MP += text('$\omega^2$',(i+.5,r-j-.5),rgbcolor='black') | MP += text(r'$\omega^2$',(i+.5,r-j-.5),rgbcolor='black') |
| Line 477: | Line 479: |
| MP += text('$\omega $',(i+.5,r-j-.5),rgbcolor='black') | MP += text(r'$\omega $',(i+.5,r-j-.5),rgbcolor='black') |
| Line 486: | Line 488: |
| MP += text('$ \pi_1$',(r/2,r+2), rgbcolor='black', fontsize=25) MP += text('$ \pi_2$',(-2.5,r/2), rgbcolor='black', fontsize=25) html('Symmetry of Primary Cubic Residues mod ' \ + '%d primary primes in $ \mathbf Z[\omega]$.'%r) |
MP += text(r'$ \pi_1$',(r/2,r+2), rgbcolor='black', fontsize=25) MP += text(r'$ \pi_2$',(-2.5,r/2), rgbcolor='black', fontsize=25) pretty_print(html('Symmetry of Primary Cubic Residues mod ' \ + r'%d primary primes in $ \mathbf Z[\omega]$.'%r)) |
| Line 644: | Line 646: |
| html('$$J(%s,%s) = %s$$'%(latex2(e),latex2(f),latex(js))) | pretty_print(html('$$J(%s,%s) = %s$$'%(latex2(e),latex2(f),latex(js)))) |
| Line 664: | Line 666: |
| html(s)}}} | pretty_print(html(s)) }}} |
| Line 754: | Line 757: |
| print "p = %s"%p show(E.change_ring(GF(p)).plot(),xmin=0,ymin=0) |
print("p = %s" % p) show(E.change_ring(GF(p)).plot(), xmin=0, ymin=0) |
| Line 778: | Line 781: |
| html(""" | pretty_print(html(""" |
| Line 804: | Line 807: |
| (g^ b)^a, g^a, b, p, (g^a)^b)) | (g^ b)^a, g^a, b, p, (g^a)^b))) |
| Line 814: | Line 817: |
crows not working |
|
| Line 817: | Line 822: |
| c = list(continued_fraction(RealField(prec)(number))); print c | c = list(continued_fraction(RealField(prec)(number))); print(c) |
| Line 826: | Line 831: |
| def _(m=selector([1..15],nrows=2), n=(7,(3..10))): | def _(m=selector([1..15],nrows=2), n=(7,[3..10])): |
| Line 828: | Line 833: |
| s = "<h3>First n=%s Bernoulli numbers attached to characters with modulus m=%s</h3>"%(n,m) s += '<table border=1>' s += '<tr bgcolor="#edcc9c"><td align=center>$\\chi$</td><td>Conductor</td>' + \ ''.join('<td>$B_{%s,\chi}$</td>'%k for k in [1..n]) + '</tr>' |
s = r"<h3>First n=%s Bernoulli numbers attached to characters with modulus m=%s</h3>"%(n,m) s += r'<table border=1>' s += r'<tr bgcolor="#edcc9c"><td align=center>$\chi$</td><td>Conductor</td>' + \ ''.join(r'<td>$B_{%s,\chi}$</td>'%k for k in [1..n]) + '</tr>' |
| Line 837: | Line 842: |
| html(s) | pretty_print(html(s)) |
| Line 846: | Line 851: |
| L = [[-0.5, 2.0^(x/100.0) - 1 + sqrt(3.0)/2] for x in xrange(1000, -1, -1)] R = [[0.5, 2.0^(x/100.0) - 1 + sqrt(3.0)/2] for x in xrange(1000)] xes = [x/1000.0 for x in xrange(-500,501,1)] |
L = [[-0.5, 2.0^(x/100.0) - 1 + sqrt(3.0)/2] for x in range(1000, -1, -1)] R = [[0.5, 2.0^(x/100.0) - 1 + sqrt(3.0)/2] for x in range(1000)] xes = [x/1000.0 for x in range(-500,501,1)] |
| Line 872: | Line 877: |
| = Multiple Zeta Values = | = Multiple Zeta Values = |
| Line 874: | Line 879: |
| == Word to composition == {{{#!sagecell @interact def _( weight=(7,(2..30))): n=weight a=[0 for i in range(n-1)] a.append(1) @interact def _(v=('word', input_grid(1, n, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] def bintocomp(a): b=[] count=1 for j in range(len(a)): if(a[j]==0): count=count+1 else: b.append(count) count=1 return(b) print "Composition is ",bintocomp(a) }}} {{attachment:akhi2.png}} == Composition to Word == {{{#!sagecell @interact def _( Depth=(7,(1..30))): n=Depth a=[] a.append(2) a=a+[1 for i in range(1,n)] @interact def _(v=('composition', input_grid(1, n, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] def comptobin(a): word=[] for i in range(len(a)): word=word+[0]*(a[i]-1)+[1] return(word) print "Word is ",comptobin(a) }}} {{attachment:akhi3.png}} == Computing Multiple Zeta values == |
== Computing Multiple Zeta values == |
| Line 926: | Line 884: |
| def _( weight=(5,(2..20))): | def _( weight=(5,(2..100))): |
| Line 979: | Line 937: |
| print zeta(a) | u=zeta(a) RIF=RealIntervalField(int(3.321928*D)) u=u/1 print(u) |
| Line 986: | Line 947: |
| def _( Depth=(5,(2..20))): n=weight |
def _( Depth=(5,(2..100))): n=Depth |
| Line 994: | Line 955: |
| def comptobin(a): word=[] for i in range(len(a)): word=word+[0]*(a[i]-1)+[1] return(word) |
|
| Line 1040: | Line 1006: |
| u=zeta(a) RIF=RealIntervalField(int(3.321928*D)) u=u/1 print(u) }}} {{attachment:akhi5.png}} == Program to Compute Integer Relation between Multiple Zeta Values == {{{#!sagecell from mpmath import * print("Enter the number of composition") @interact def _( n=(5,(2..100))): a=[] for i in range(n): a.append([i+2,1]) print("In each box Enter composition as an array") @interact def _(v=('Compositions', input_box( default=a, to_value=lambda x: vector(flatten(x)))), accuracy=(100..100000)): D=accuracy R=RealField(10) a=v def comptobin(a): word=[] for i in range(len(a)): word=word+[0]*(a[i]-1)+[1] return(word) DD=int(D)+int(R(log(3.321928*D))/R(log(10)))+4 RIF=RealIntervalField(DD) mp.dps=DD def Li(word): n=int(DD*log(10)/log(2))+1 B=[] L=[] S=[] count=-1 k=len(word) for i in range(k): B.append(mpf('0')) L.append(mpf('0')) if(word[i]==1 and i<k-1): S.append(mpf('0')) count=count+1 T=mpf('1') for m in range(n): T=T/2 B[k-1]=mpf('1')/(m+1) j=count for i in range(k-2,-1,-1): if(word[i]==0): B[i]=B[i+1]/(m+1) elif(word[i]==1): B[i]=S[j]/(m+1) S[j]=S[j]+B[i+1] j=j-1 L[i]=T*B[i]+L[i] L[k-1]=T*B[k-1]+L[k-1] return(L) def dual(a): b=list() b=a b=b[::-1] for i in range(len(b)): b[i]=1-b[i] return(b) def zeta(a): b=dual(a) l1=Li(a)+[1] l2=Li(b)+[1] Z=mpf('0') for i in range(len(l1)): Z=Z+l1[i]*l2[len(a)-i] return(Z) zet=[] for i in range(n): zet.append((zeta(comptobin(a[i])))) mp.dps=D for i in range(n): zet[i]=zet[i]/1 print("zeta(", a[i], ")=", zet[i]) u=pslq(zet,tol=10**-D,maxcoeff=100,maxsteps=10000) print("the Intger Relation between the above zeta values given by the vector") print(u) }}} {{attachment:akhi10.png}} == Word to composition == {{{#!sagecell @interact def _( weight=(7,(2..100))): n=weight a=[0 for i in range(n-1)] a.append(1) @interact def _(v=('word', input_grid(1, n, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] def bintocomp(a): b=[] count=1 for j in range(len(a)): if(a[j]==0): count=count+1 else: b.append(count) count=1 return(b) print("Composition is {}".format(bintocomp(a))) }}} {{attachment:akhi2.png}} == Composition to Word == {{{#!sagecell @interact def _( Depth=(7,(1..100))): n=Depth a=[] a.append(2) a=a+[1 for i in range(1,n)] @interact def _(v=('composition', input_grid(1, n, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] |
|
| Line 1046: | Line 1131: |
| print zeta(a) }}} {{attachment:akhi1.png}} |
print("Word is {}".format(comptobin(a))) }}} {{attachment:akhi3.png}} == Dual of a Word == {{{#!sagecell @interact def _( weight=(7,(2..100))): n=weight a=[0 for i in range(n-1)] a.append(1) @interact def _(v=('word', input_grid(1, n, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] def dual(a): b=list() b=a b=b[::-1] for i in range(len(b)): b[i]=1-b[i] return(b) print("Dual word is {}"?format(dual(a))) }}} {{attachment:akhi4.png}} == Shuffle product of two Words == {{{#!sagecell @interact def _( w1=(2,(2..100)), w2=(2,(2..100))): a=[0] b=[0 for i in range(w2-1)] a=a+[1 for i in range(1,w1)] b=b+[1] import itertools #this program gives the list of all binary words of weight n and depth k @interact def _(v1=('word1', input_grid(1, w1, default=[a], to_value=lambda x: vector(flatten(x)))), v2=('word2', input_grid(1, w2, default=[b], to_value=lambda x: vector(flatten(x))))): a=[v1[i] for i in range(len(v1))] b=[v2[i] for i in range(len(v2))] def kbits(n, k): result = [] for bits in itertools.combinations(range(n), k): s = ['0'] * n for bit in bits: s[bit] = '1' result.append(''.join(s)) return result def sort(a,l,m): b=[] n=len(a) for i in range(n): b.append(a[i]) for j in range(l-1,-1,-1): k=0 for t in range(m+1): for i in range(n): if(a[i][j]== t): b[k]=a[i] k=k+1 for i in range(n): a[i]=b[i] return(a) def count(a): n=len(a) b=[] b.append(a[0]) m=[] m.append(1) c=0 for i in range(1,n): if(a[i]==a[i-1]): m[c]=m[c]+1 else: b.append(a[i]) m.append(1) c=c+1 return(b,m) def shuffle(a,b): r=len(a) s=len(b) # Generating an array of strings containing all combinations of weight r+s and depth s M=kbits(r+s,s) n=len(M) a1= [] for i in range(n): a1.append(list(M[i])) # The zeroes are replaced by the entries of a and the ones by the entries of b a2= [] for i in range(n): a2.append([]) count0=0 count1=0 for j in range(s+r): if(a1[i][j]=='0'): a2[i].append(a[count0]) count0=count0+1 if(a1[i][j]=='1'): a2[i].append(b[count1]) count1=count1+1 # Reordering in lexicographic order the entries of a2: this is done by first reordering them according to the last digit, then the next to last digit, etc a3=sort(a2,r+s,max(a+b+[0])) # Getting the same list without repetitions and with multiplicities a4=count(a3) return(a4) c=shuffle(a,b) for i in range(len(c[0])-1): print(c[1][i],"*",c[0][i] ,"+ ") print(c[1][len(c[0])-1],"*",c[0][len(c[0])-1]) }}} {{attachment:akhi6.png}} == Shuffle Regularization at 0 == {{{#!sagecell @interact def _( w=(2,(2..100))): a=[0] a=a+[1 for i in range(1,w)] import itertools #this program gives the list of all binary words of weight n and depth k @interact def _(v=('word', input_grid(1, w, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] def kbits(n, k): result = [] for bits in itertools.combinations(range(n), k): s = ['0'] * n for bit in bits: s[bit] = '1' result.append(''.join(s)) return result def sort(a,l,m): b=[] n=len(a) for i in range(n): b.append(a[i]) for j in range(l-1,-1,-1): k=0 for t in range(m+1): for i in range(n): if(a[i][j]== t): b[k]=a[i] k=k+1 for i in range(n): a[i]=b[i] return(a) def sort1(a,l,m): b=[] b.append([]) b.append([]) n=len(a[0]) for i in range(n): b[0].append(a[0][i]) b[1].append(a[1][i]) for j in range(l-1,-1,-1): k=0 for t in range(m+1): for i in range(n): if(a[0][i][j]== t): b[0][k]=a[0][i] b[1][k]=a[1][i] k=k+1 for i in range(n): a[0][i]=b[0][i] a[1][i]=b[1][i] return(a) def count(a): n=len(a) b=[] b.append(a[0]) m=[] m.append(1) c=0 for i in range(1,n): if(a[i]==a[i-1]): m[c]=m[c]+1 else: b.append(a[i]) m.append(1) c=c+1 return(b,m) def count1(a): n=len(a[0]) b=[] b.append([]) b.append([]) b[0].append(a[0][0]) b[1].append(a[1][0]) c=0 for i in range(1,n): if(a[0][i]==a[0][i-1]): b[1][c]=b[1][c]+a[1][i] else: b[0].append(a[0][i]) b[1].append(a[1][i]) c=c+1 return(b) def shuffle(a,b): r=len(a) s=len(b) # Generating an array of strings containing all combinations of weight r+s and depth s M=kbits(r+s,s) n=len(M) a1= [] for i in range(n): a1.append(list(M[i])) # The zeroes are replaced by the entries of a and the ones by the entries of b a2= [] for i in range(n): a2.append([]) count0=0 count1=0 for j in range(s+r): if(a1[i][j]=='0'): a2[i].append(a[count0]) count0=count0+1 if(a1[i][j]=='1'): a2[i].append(b[count1]) count1=count1+1 # Reordering in lexicographic order the entries of a2: this is done by first reordering them according to the last digit, then the next to last digit, etc a3=sort(a2,r+s,max(a+b+[0])) # Getting the same list without repetitions and with multiplicities a4=count(a3) return(a4) def Regshuf0(a): r=[] r.append([]) r.append([]) t=0 c=1 for i in range(len(a)+1): if(t==0): b=shuffle(a[:len(a)-i],a[len(a)-i:]) for j in range(len(b[0])): r[0].append(b[0][j]) r[1].append(b[1][j]*c) c=-c if(i<len(a)): if(a[len(a)-1-i]==1): t=1 r=sort1(r,len(a),max(a+[0])) r=count1(r) rg=[] rg.append([]) rg.append([]) for i in range(len(r[0])): if(r[1][i] is not 0): rg[0].append(r[0][i]) rg[1].append(r[1][i]) return(rg) c = Regshuf0(a) for i in range(len(c[0])-1): if(c[1][i] != 0): print(c[1][i],"*",c[0][i] ,"+ ") if(c[1][len(c[0])-1] != 0): print(c[1][len(c[0])-1],"*",c[0][len(c[0])-1]) }}} {{attachment:akhi7.png}} == Shuffle Regularization at 1 == {{{#!sagecell @interact def _( w=(2,(2..20))): a=[0] a=a+[1 for i in range(1,w)] import itertools #this program gives the list of all binary words of weight n and depth k @interact def _(v=('word', input_grid(1, w, default=[a], to_value=lambda x: vector(flatten(x))))): a=[v[i] for i in range(len(v))] def kbits(n, k): result = [] for bits in itertools.combinations(range(n), k): s = ['0'] * n for bit in bits: s[bit] = '1' result.append(''.join(s)) return result def sort(a,l,m): b=[] n=len(a) for i in range(n): b.append(a[i]) for j in range(l-1,-1,-1): k=0 for t in range(m+1): for i in range(n): if(a[i][j]== t): b[k]=a[i] k=k+1 for i in range(n): a[i]=b[i] return(a) def sort1(a,l,m): b=[] b.append([]) b.append([]) n=len(a[0]) for i in range(n): b[0].append(a[0][i]) b[1].append(a[1][i]) for j in range(l-1,-1,-1): k=0 for t in range(m+1): for i in range(n): if(a[0][i][j]== t): b[0][k]=a[0][i] b[1][k]=a[1][i] k=k+1 for i in range(n): a[0][i]=b[0][i] a[1][i]=b[1][i] return(a) def count(a): n=len(a) b=[] b.append(a[0]) m=[] m.append(1) c=0 for i in range(1,n): if(a[i]==a[i-1]): m[c]=m[c]+1 else: b.append(a[i]) m.append(1) c=c+1 return(b,m) def count1(a): n=len(a[0]) b=[] b.append([]) b.append([]) b[0].append(a[0][0]) b[1].append(a[1][0]) c=0 for i in range(1,n): if(a[0][i]==a[0][i-1]): b[1][c]=b[1][c]+a[1][i] else: b[0].append(a[0][i]) b[1].append(a[1][i]) c=c+1 return(b) def shuffle(a,b): r=len(a) s=len(b) # Generating an array of strings containing all combinations of weight r+s and depth s M=kbits(r+s,s) n=len(M) a1= [] for i in range(n): a1.append(list(M[i])) # The zeroes are replaced by the entries of a and the ones by the entries of b a2= [] for i in range(n): a2.append([]) count0=0 count1=0 for j in range(s+r): if(a1[i][j]=='0'): a2[i].append(a[count0]) count0=count0+1 if(a1[i][j]=='1'): a2[i].append(b[count1]) count1=count1+1 # Reordering in lexicographic order the entries of a2: this is done by first reordering them according to the last digit, then the next to last digit, etc a3=sort(a2,r+s,max(a+b+[0])) # Getting the same list without repetitions and with multiplicities a4=count(a3) return(a4) def Regshuf1(a): r=[] r.append([]) r.append([]) t=0 c=1 for i in range(len(a)+1): if(t==0): b=shuffle(a[:i],a[i:]) for j in range(len(b[0])): r[0].append(b[0][j]) r[1].append(b[1][j]*c) c=-c if(i<len(a)): if(a[i]==0): t=1 r=sort1(r,len(a),max(a+[0])) r=count1(r) rg=[] rg.append([]) rg.append([]) for i in range(len(r[0])): if(r[1][i] is not 0): rg[0].append(r[0][i]) rg[1].append(r[1][i]) return(rg) c = Regshuf1(a) for i in range(len(c[0])-1): if(c[1][i] != 0): print(c[1][i],"*",c[0][i] ,"+ ") if(c[1][len(c[0])-1] != 0): print(c[1][len(c[0])-1],"*",c[0][len(c[0])-1]) }}} {{attachment:akhi8.png}} |
Contents
Integer Factorization
Divisibility Poset
by William Stein
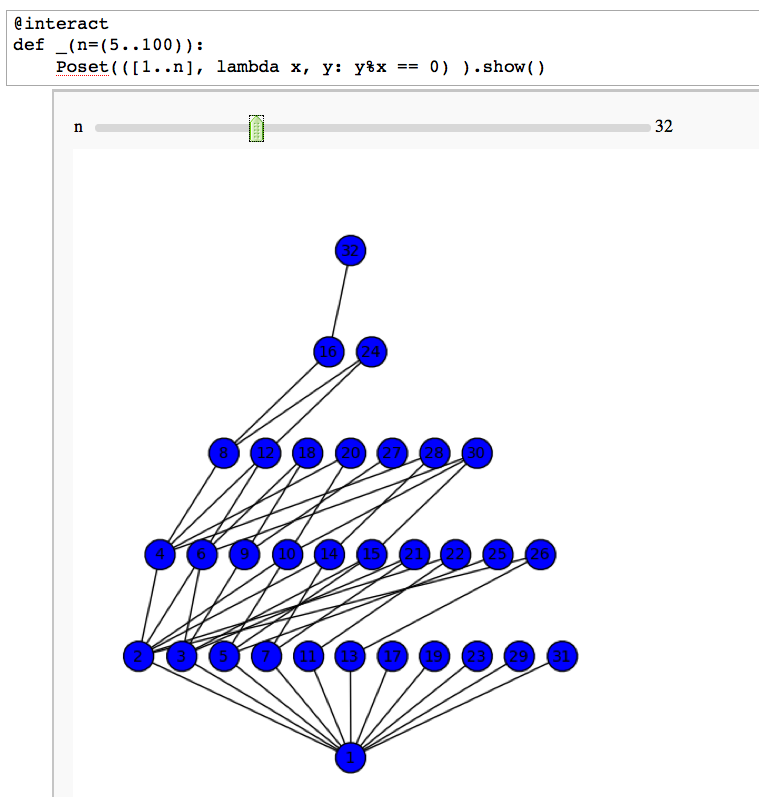
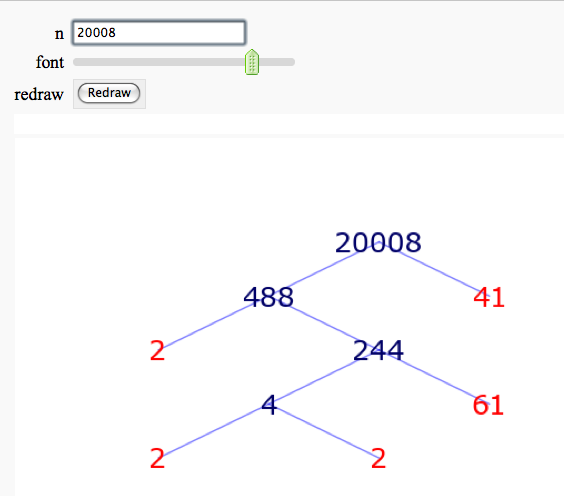
Factor Trees
by William Stein
More complicated demonstration using Mathematica: http://demonstrations.wolfram.com/FactorTrees/
Factoring an Integer
by Timothy Clemans
Sage implementation of the Mathematica demonstration of the same name. http://demonstrations.wolfram.com/FactoringAnInteger/
Prime Numbers
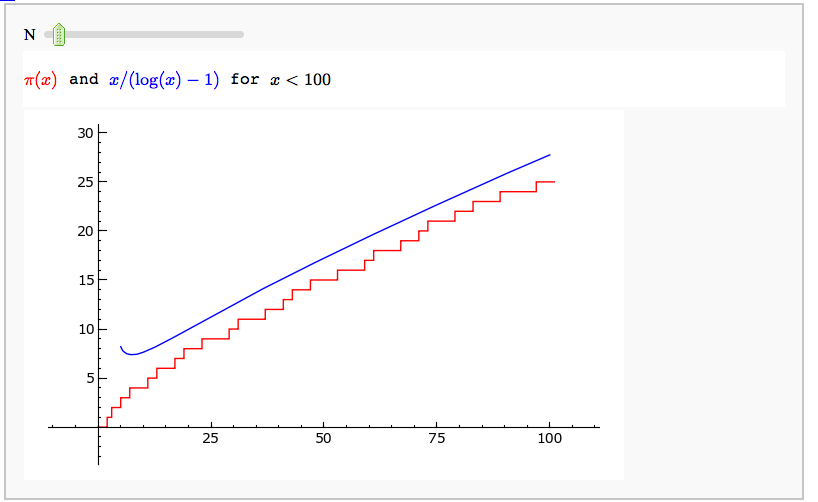
Illustrating the prime number theorem
by William Stein
Prime Spiral - Square FIXME
by David Runde
Prime Spiral - Polar
by David Runde
Needs fix for show_factors
Modular Forms
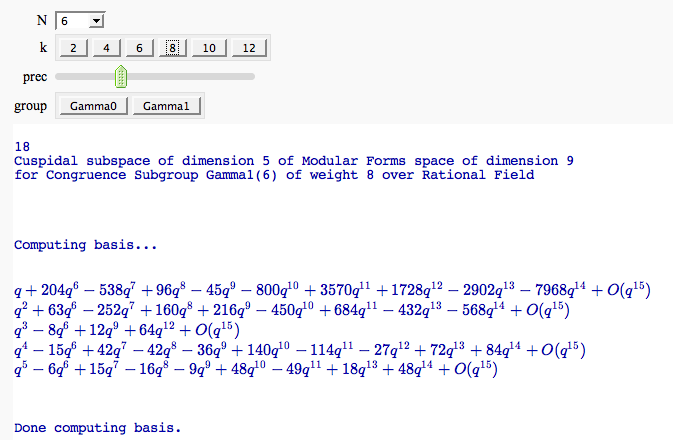
Computing modular forms
by William Stein
Computing the cuspidal subgroup
by William Stein
ncols not working
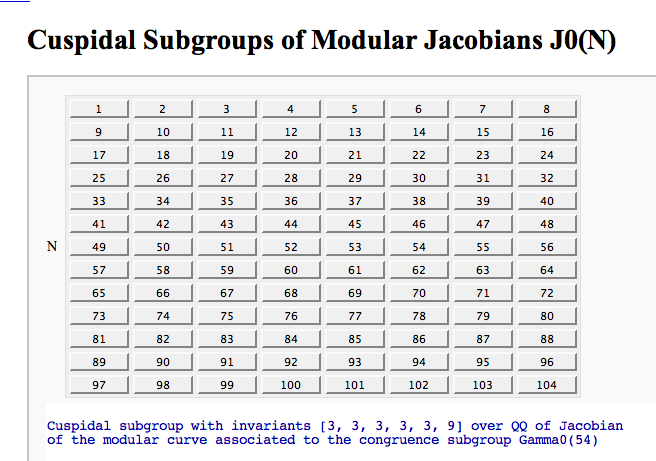
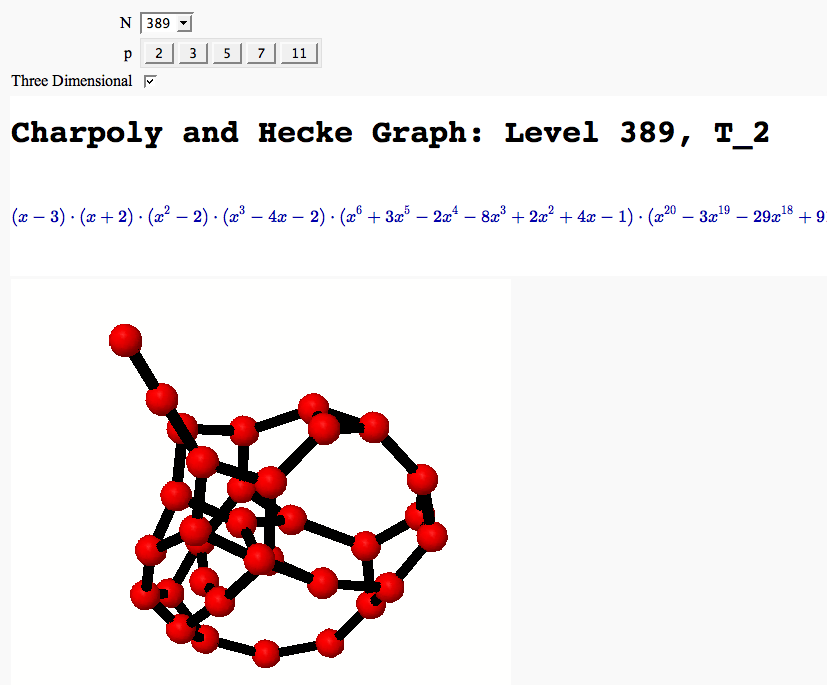
A Charpoly and Hecke Operator Graph
by William Stein
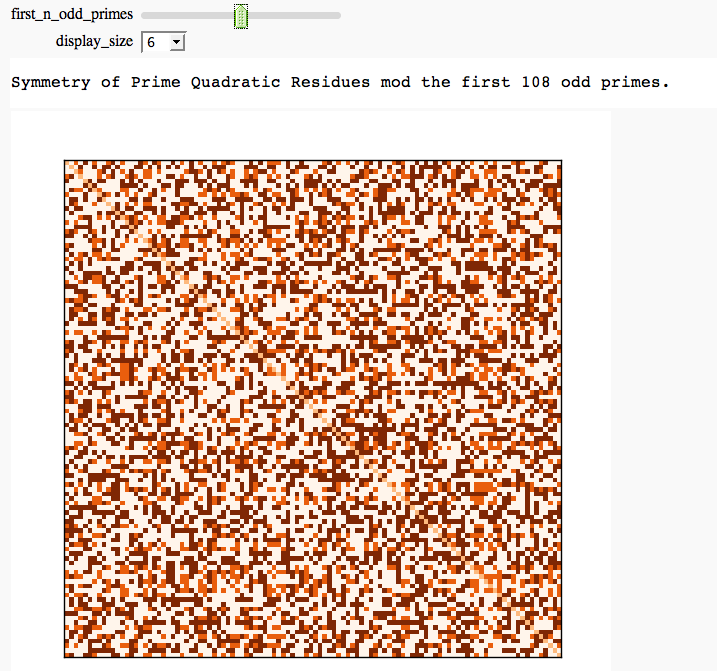
Modular Arithmetic
Quadratic Residue Table FIXME
by Emily Kirkman

Cubic Residue Table FIXME
by Emily Kirkman

Cyclotomic Fields
Gauss and Jacobi Sums in Complex Plane
by Emily Kirkman
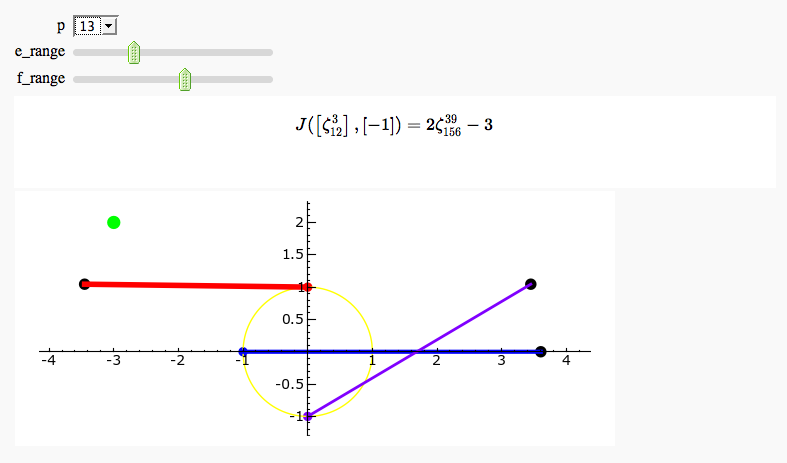
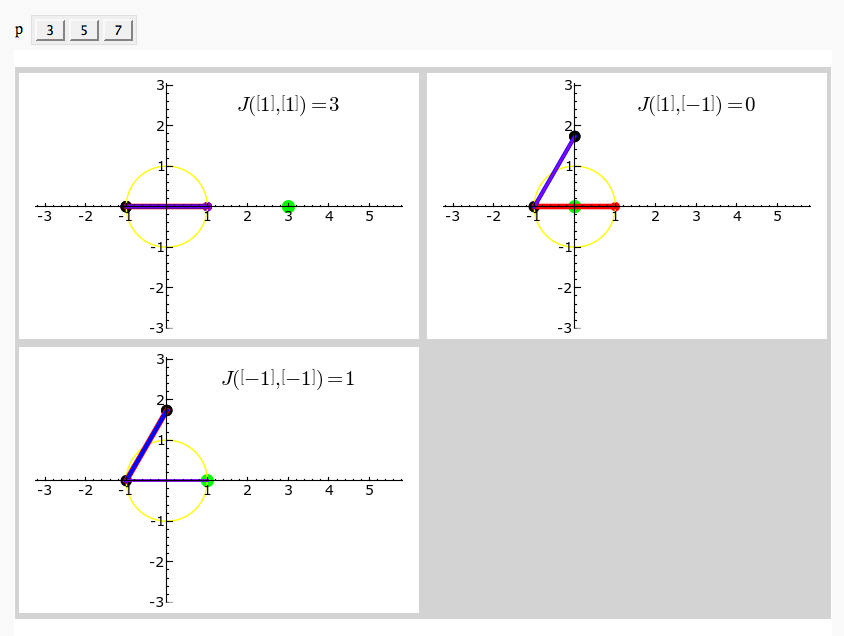
Exhaustive Jacobi Plotter
by Emily Kirkman
Elliptic Curves
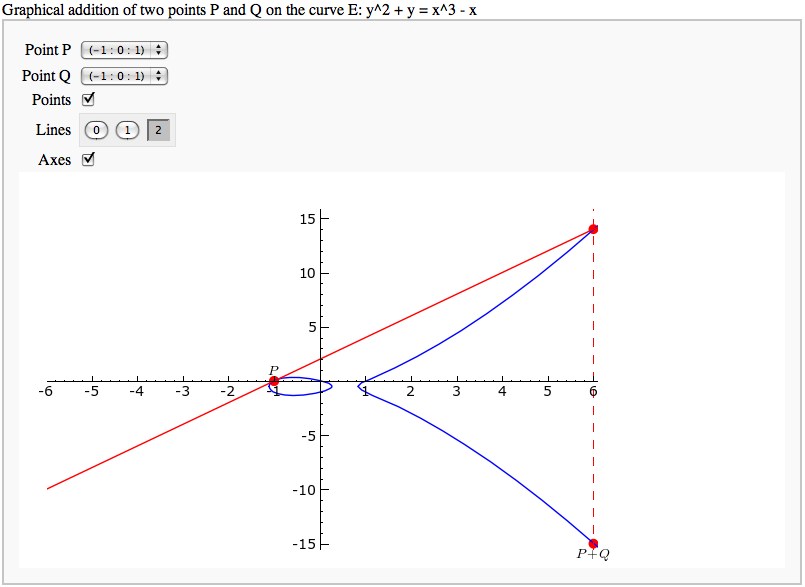
Adding points on an elliptic curve
by David Møller Hansen
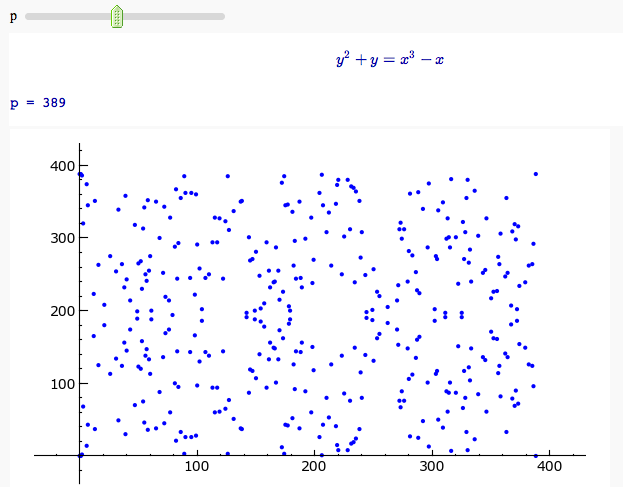
Plotting an elliptic curve over a finite field
Cryptography
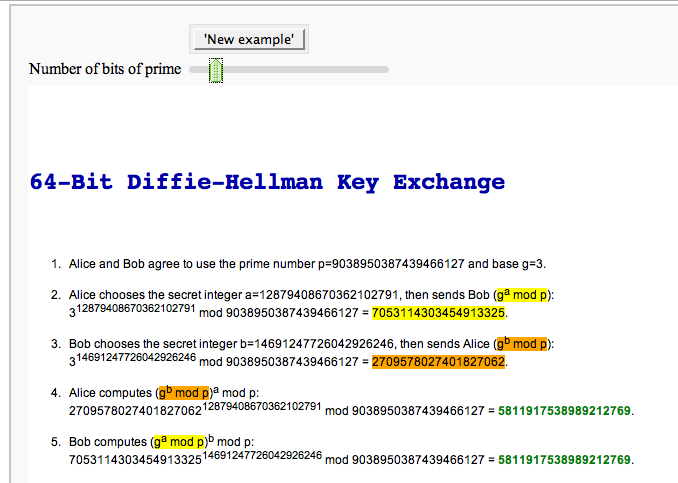
The Diffie-Hellman Key Exchange Protocol
by Timothy Clemans and William Stein
Other
Continued Fraction Plotter
by William Stein
crows not working
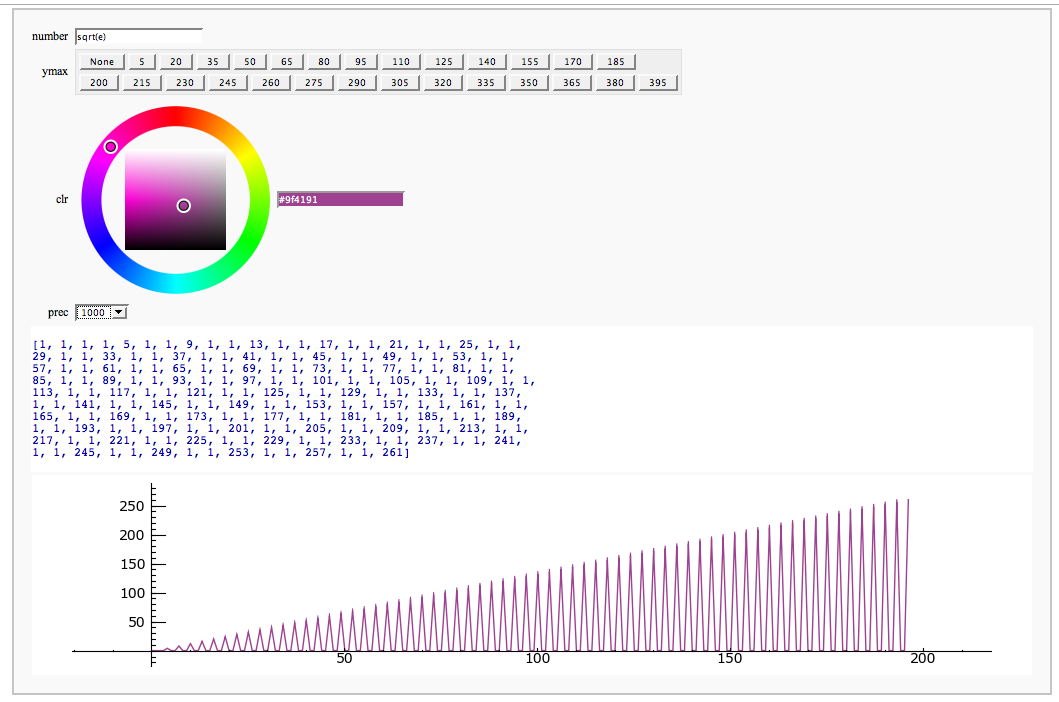
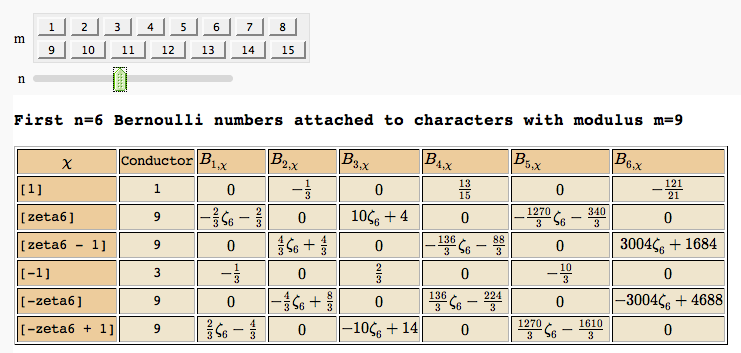
Computing Generalized Bernoulli Numbers
by William Stein (Sage-2.10.3)
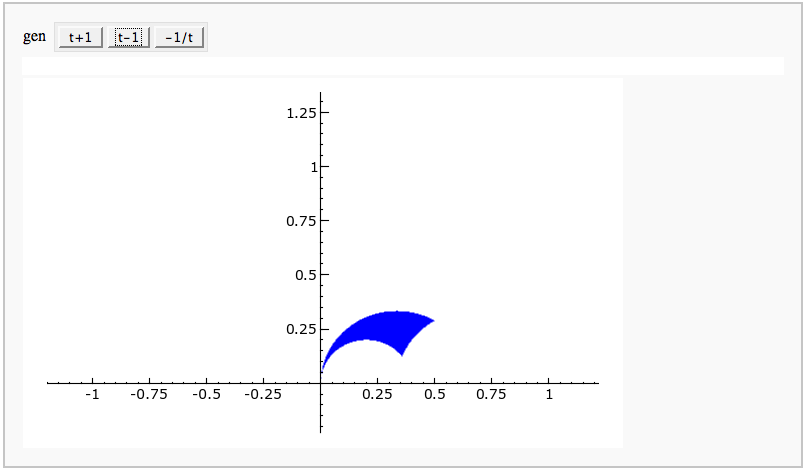
Fundamental Domains of SL_2(ZZ)
by Robert Miller
Multiple Zeta Values
by Akhilesh P.
Computing Multiple Zeta values
Word Input

Composition Input

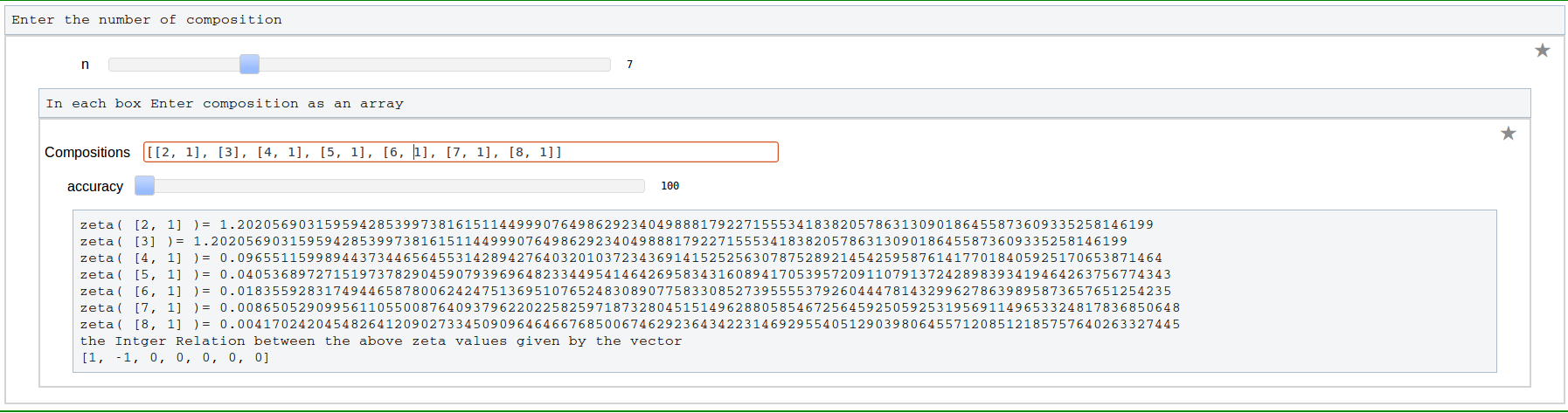
Program to Compute Integer Relation between Multiple Zeta Values
Word to composition

Composition to Word

Dual of a Word

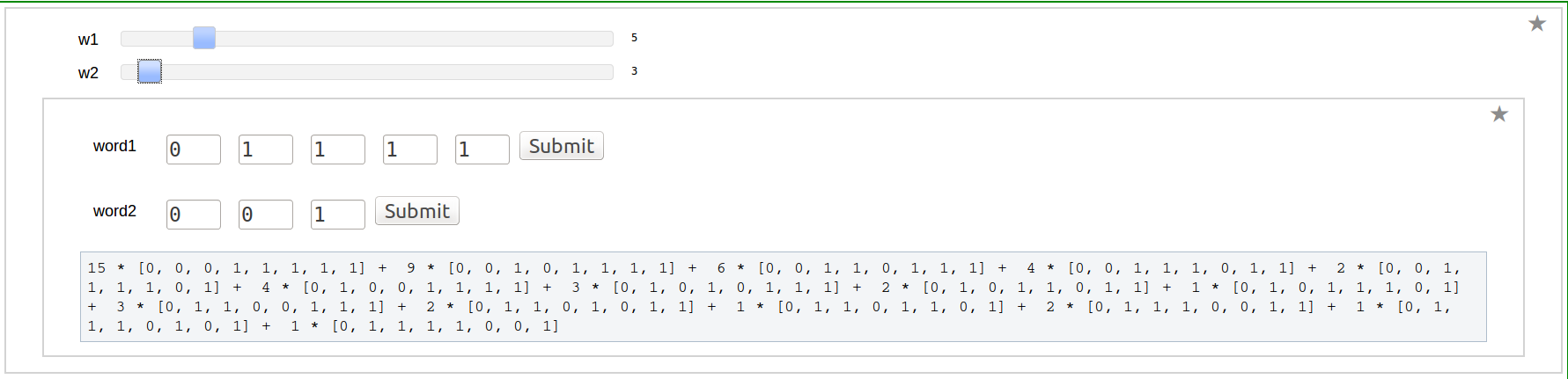
Shuffle product of two Words
Shuffle Regularization at 0

Shuffle Regularization at 1

