|
Size: 30348
Comment: fixed Continued Fraction Plotter, more or less
|
Size: 32040
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 871: | Line 871: |
= Multiple Zeta Values = by Akhilesh P. == Computing Multiple Zeta values == {{{#!sagecell R=RealField(10) @interact def _(v=('vector', input_grid(1, 5, default=[[0,0,0,0,1]], to_value=lambda x: vector(flatten(x)))), accuracy=(100..100000)): D=accuracy a=[v[i] for i in range(len(v))] DD=int(3.321928*D)+int(R(log(3.321928*D))/R(log(10)))+4 RIF=RealIntervalField(DD) def Li(word): n=int(DD*log(10)/log(2))+1 B=[] L=[] S=[] count=-1 k=len(word) for i in range(k): B.append(RIF('0')) L.append(RIF('0')) if(word[i]==1 and i<k-1): S.append(RIF('0')) count=count+1 T=RIF('1') for m in range(n): T=T/2 B[k-1]=RIF('1')/(m+1) j=count for i in range(k-2,-1,-1): if(word[i]==0): B[i]=B[i+1]/(m+1) elif(word[i]==1): B[i]=S[j]/(m+1) S[j]=S[j]+B[i+1] j=j-1 L[i]=T*B[i]+L[i] L[k-1]=T*B[k-1]+L[k-1] return(L) def dual(a): b=list() b=a b=b[::-1] for i in range(len(b)): b[i]=1-b[i] return(b) def zeta(a): b=dual(a) l1=Li(a)+[1] l2=Li(b)+[1] Z=RIF('0') for i in range(len(l1)): Z=Z+l1[i]*l2[len(a)-i] return(Z) print zeta(a) }}} |
Contents
Integer Factorization
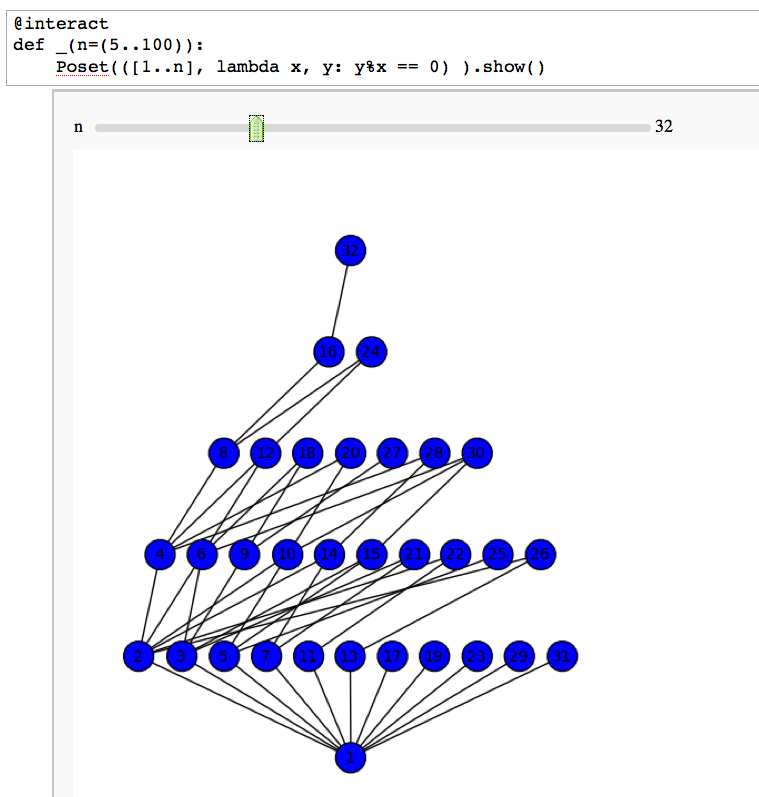
Divisibility Poset
by William Stein
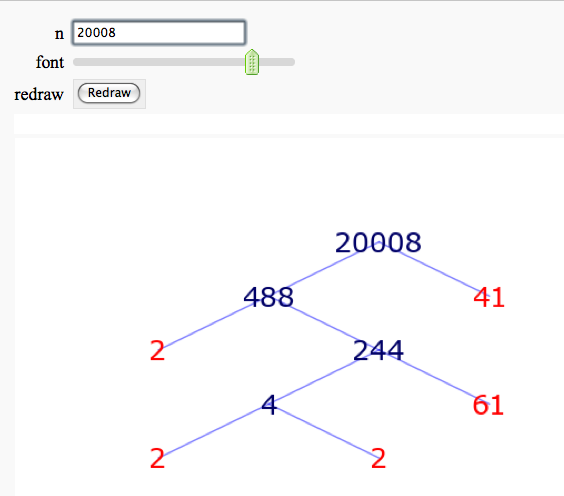
Factor Trees
by William Stein
More complicated demonstration using Mathematica: http://demonstrations.wolfram.com/FactorTrees/
Factoring an Integer
by Timothy Clemans
Sage implementation of the Mathematica demonstration of the same name. http://demonstrations.wolfram.com/FactoringAnInteger/
Prime Numbers
Illustrating the prime number theorem
by William Stein
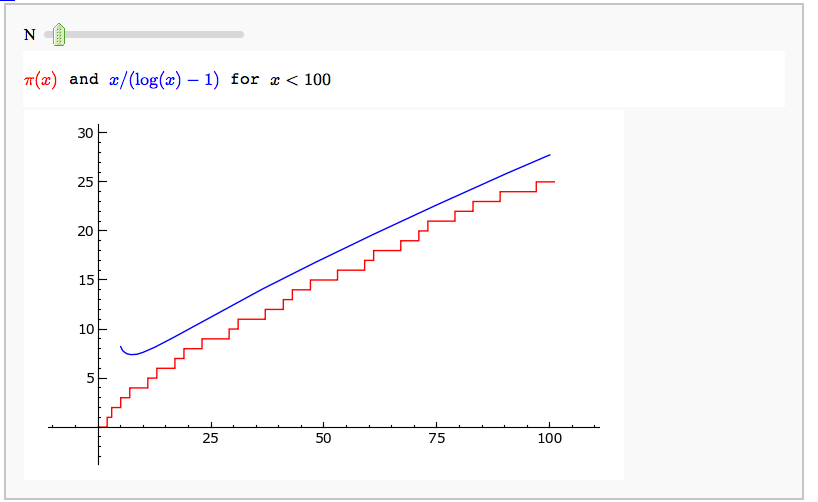
Prime Spiral - Square FIXME
by David Runde
Prime Spiral - Polar
by David Runde
Modular Forms
Computing modular forms
by William Stein
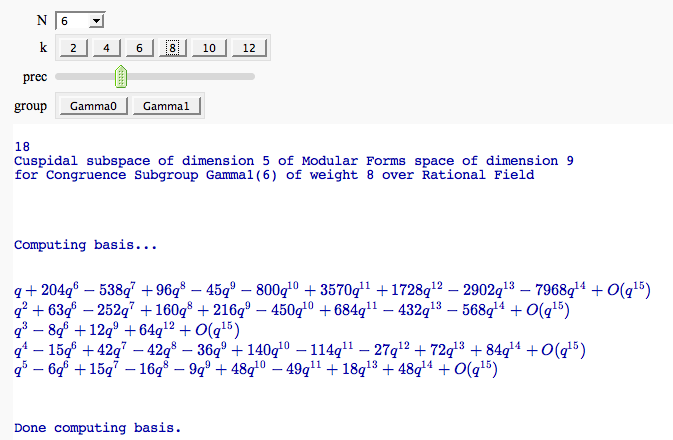
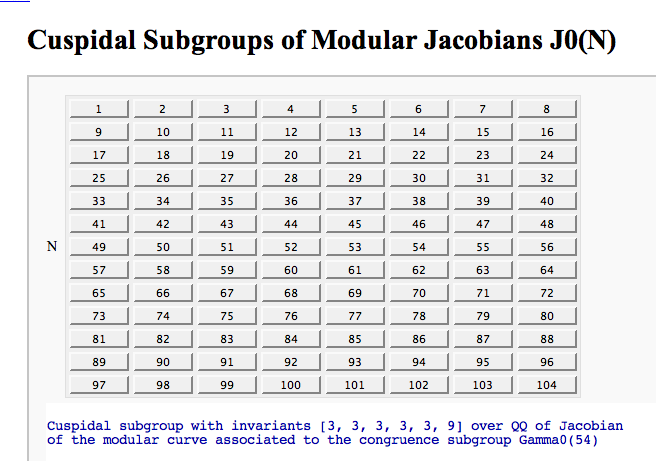
Computing the cuspidal subgroup
by William Stein
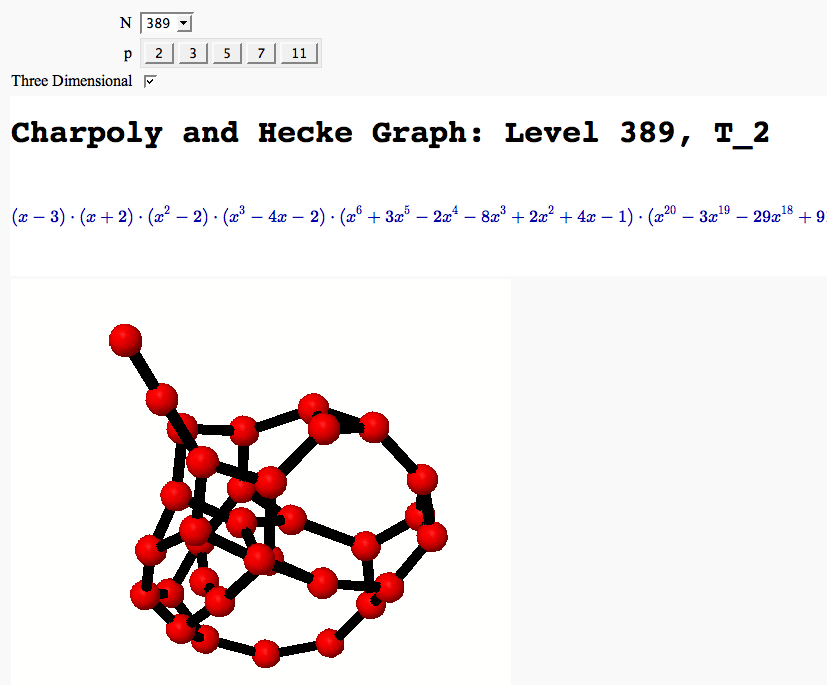
A Charpoly and Hecke Operator Graph
by William Stein
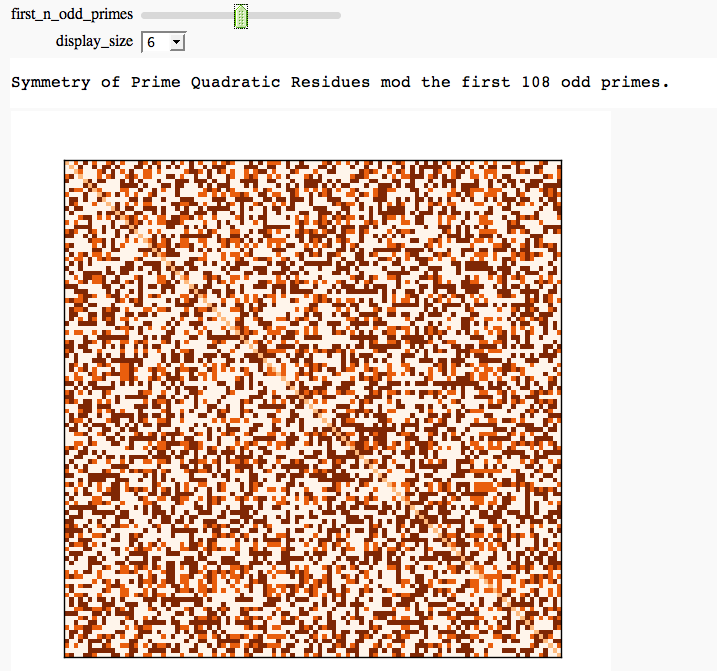
Modular Arithmetic
Quadratic Residue Table FIXME
by Emily Kirkman

Cubic Residue Table FIXME
by Emily Kirkman

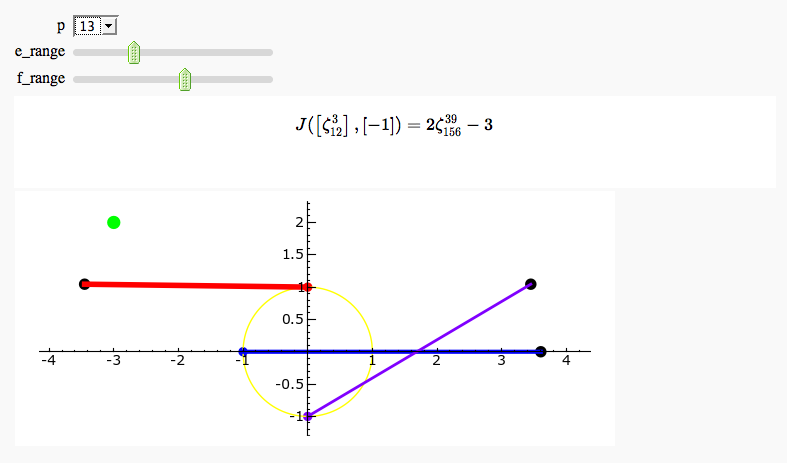
Cyclotomic Fields
Gauss and Jacobi Sums in Complex Plane
by Emily Kirkman
Exhaustive Jacobi Plotter
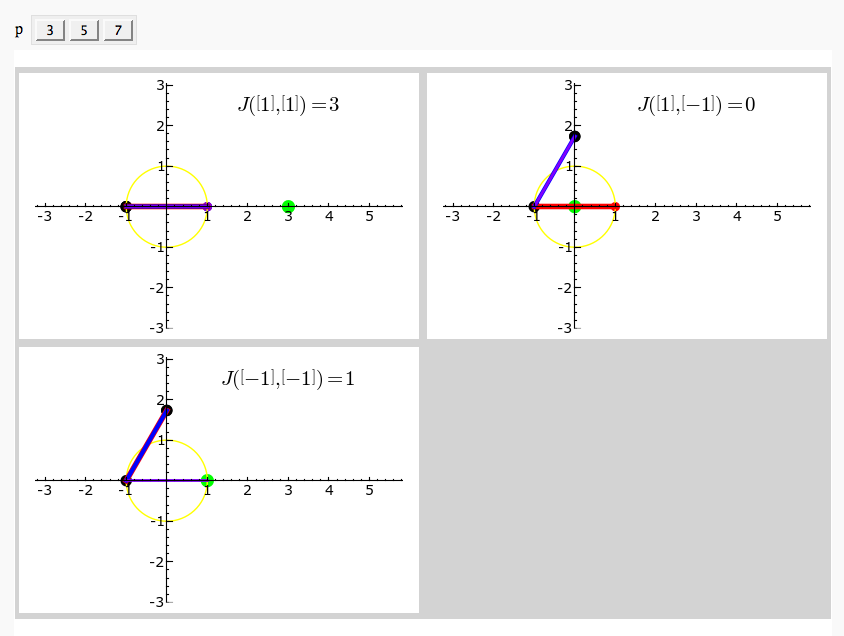
by Emily Kirkman
Elliptic Curves
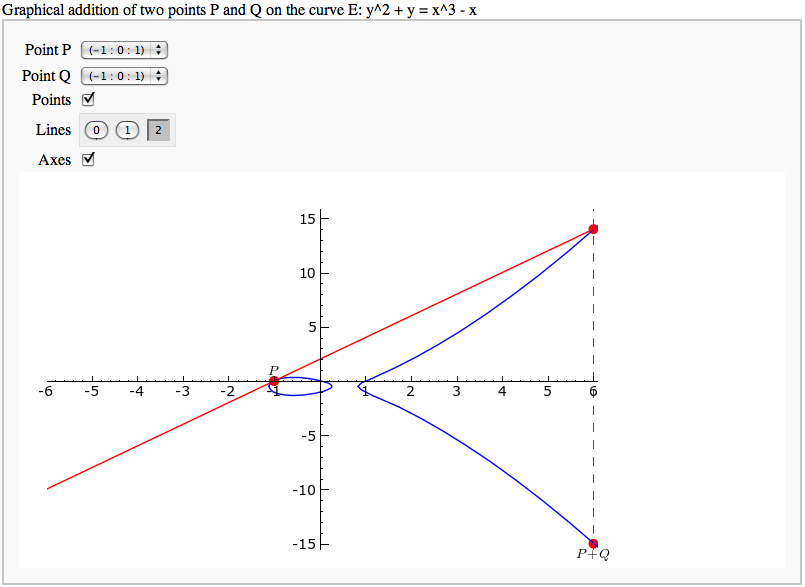
Adding points on an elliptic curve
by David Møller Hansen
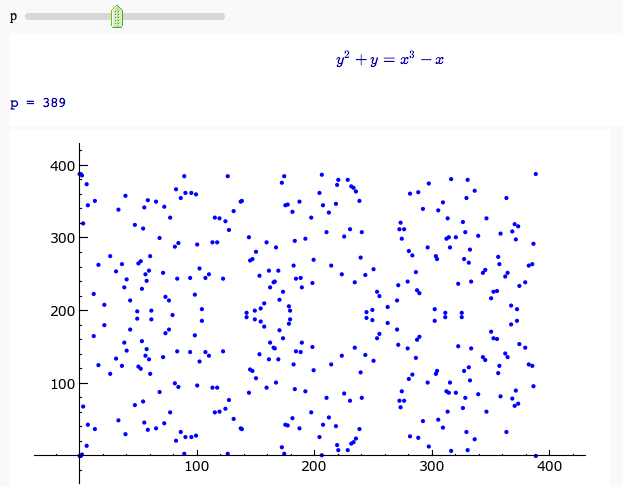
Plotting an elliptic curve over a finite field
Cryptography
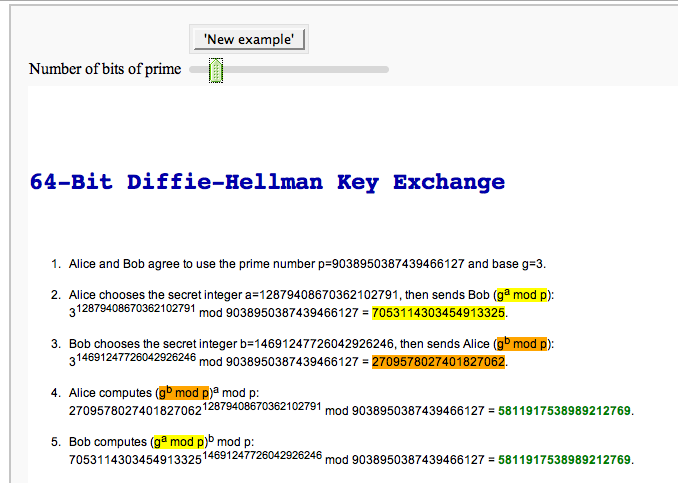
The Diffie-Hellman Key Exchange Protocol
by Timothy Clemans and William Stein
Other
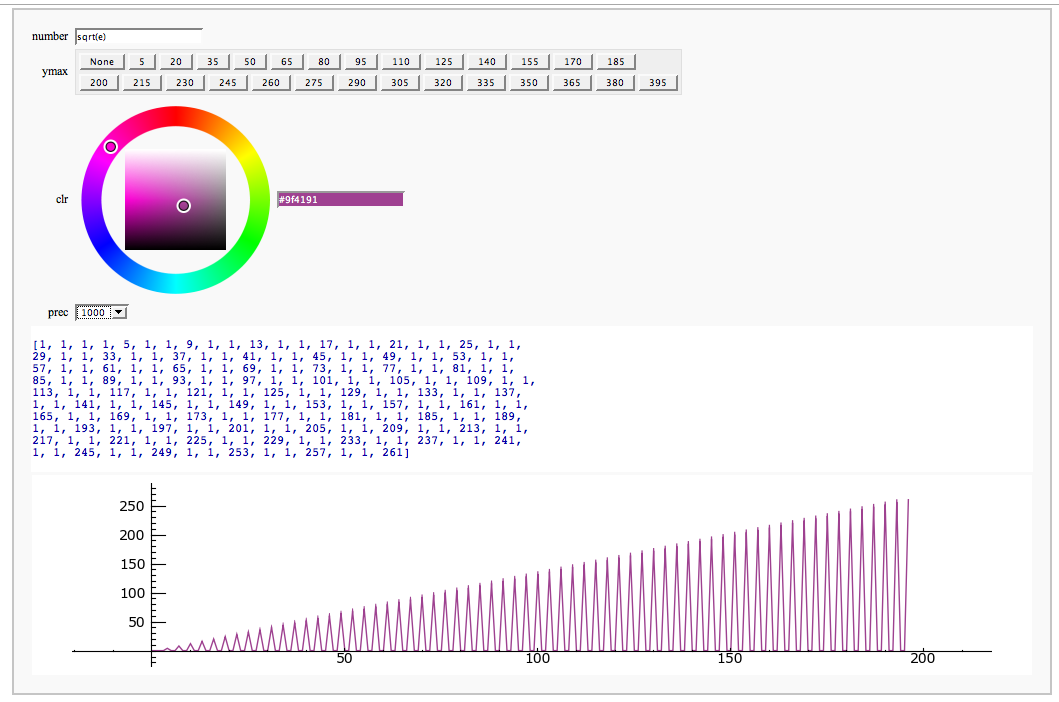
Continued Fraction Plotter
by William Stein
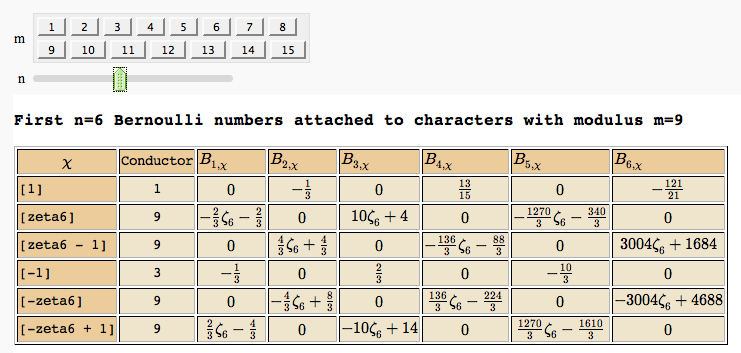
Computing Generalized Bernoulli Numbers
by William Stein (Sage-2.10.3)
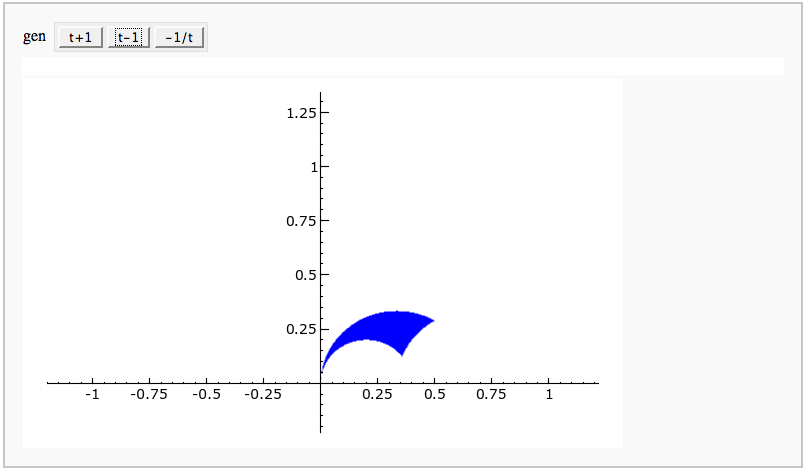
Fundamental Domains of SL_2(ZZ)
by Robert Miller
Multiple Zeta Values
by Akhilesh P.
Computing Multiple Zeta values
