|
Size: 7477
Comment:
|
Size: 32114
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| = Sage Interactions - Number Theory = goto [:interact:interact main page] |
<<TableOfContents>> = Integer Factorization = == Divisibility Poset == by William Stein {{{#!sagecell @interact def _(n=(5..100)): Poset(([1..n], lambda x, y: y%x == 0) ).show() }}} {{attachment:divposet.png}} |
| Line 6: | Line 18: |
| {{{ | {{{#!sagecell |
| Line 39: | Line 51: |
| g += line([(j*2-len(cur),-i), ((k*2)-len(rows[i-1]),-i+1)], | g += line([(j*2-len(cur),-i), ((k*2)-len(rows[i-1]),-i+1)], |
| Line 51: | Line 63: |
| attachment:factortree.png === Continued Fraction Plotter === |
{{attachment:factortree.png}} More complicated demonstration using Mathematica: http://demonstrations.wolfram.com/FactorTrees/ == Factoring an Integer == by Timothy Clemans Sage implementation of the Mathematica demonstration of the same name. http://demonstrations.wolfram.com/FactoringAnInteger/ {{{#!sagecell @interact def _(r=selector(range(0,10000,1000), label='range', buttons=True), n=slider(0,1000,1,2,'n',False)): if not r and n in (0, 1): n = 2 s = '$%d = %s$' % (r + n, factor(r + n)) s = s.replace('*', '\\times') html(s) }}} = Prime Numbers = == Illustrating the prime number theorem == |
| Line 55: | Line 86: |
| {{{ @interact def _(number=e, ymax=selector([None,5,20,..,400],nrows=2), clr=Color('purple'), prec=[500,1000,..,5000]): c = list(continued_fraction(RealField(prec)(number))); print c show(line([(i,z) for i, z in enumerate(c)],rgbcolor=clr),ymax=ymax,figsize=[10,2]) }}} attachment:contfracplot.png === Illustrating the prime number thoerem === by William Stein {{{ |
{{{#!sagecell |
| Line 71: | Line 92: |
| attachment:primes.png === Computing Generalized Bernoulli Numbers === |
{{attachment:primes.png}} == Prime Spiral - Square FIXME == by David Runde {{{#!sagecell @interact def square_prime_spiral(start=1, end=100, size_limit = 10, show_lines=false, invert=false, x_cord=0, y_cord=0, n = 0): """ REFERENCES: Alpern, Dario. "Ulam's Spiral". http://www.alpertron.com.ar/ULAM.HTM Sacks, Robert. http://www.NumberSpiral.com Ventrella, Jeffery. "Prime Numbers are the Holes Behind Complex Composite Patterns". http://www.divisorplot.com Williamson, John. Number Spirals. http://www.dcs.gla.ac.uk/~jhw/spirals/index.html [email protected] Weisstein, Eric W. "Prime-Generating Polynomial." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Prime-GeneratingPolynomial.html """ #Takes an (x,y) coordinate (and the start of the spiral) and gives its corresponding n value def find_n(x,y, start): if x>0 and y>-x and y<=x: return 4*(x-1)^2 + 5*(x-1) + (start+1) + y elif x<=0 and y>=x and y<=-x: return 4*x^2 - x + (start) -y elif y>=0 and -y+1 <= x and y-1 >= x: return 4*y^2 -y + start -x elif y<0 and -x >= y and y<x: return 4*(y+1)^2 -11*(y+1) + (start+7) +x else: print 'NaN' #Takes in an n and the start value of the spiral and gives its (x,y) coordinate def find_xy(num, start): num = num - start +1 bottom = floor(sqrt(num)) top = ceil(sqrt(num)) if bottom^2 < num and num<=bottom^2+bottom+1: if bottom%2 == 0: x=-bottom/2 y=-x-(num-bottom^2)+1 else: x=bottom/2+1/2 y=-x + (num-bottom^2) else: if top%2 == 0: y=top/2 x=-top/2+1+top^2-num else: y=-top/2+1/2 x=top/2 -1/2 - (top^2-num) x = Integer(x) y = Integer(y) return (x,y) if start < 1 or end <=start: print "invalid start or end value" if n > end: print "WARNING: n is larger than the end value" #Changes the entry of a matrix by taking the old matrix and the (x,y) coordinate (in matrix coordinates) and returns the changed matrix def matrix_morph(M, x, y, set): N = copy(M) N[x-1,y] = set M = N return M #These functions return an int based on where the t is located in the spiral def SW_NE(t, x, y, start): if -y<x: return 4*t^2 + 2*t -x+y+start else: return 4*t^2 + 2*t +x-y+start def NW_SE(t, x, y, start): if x<y: return 4*t^2 -x-y+start else: return 4*t^2 + 4*t +x+y+start size = ceil(sqrt(end-start+1)) #Size of the matrix num=copy(start) # Start number (might not be used) x = ceil(size/2) #starting center x of the matrix (in matrix coordinates) y = copy(x) #starting center y of the matrix (in matrix coordinates) if n !=0: x_cord, y_cord = find_xy(n, start) #Overrides the user given x and y coordinates xt = copy(x_cord) yt = copy(y_cord) countx=0 county=0 overcount = 1 if size <= size_limit: M = matrix(ZZ, size+1) # Allows the numbers to be seen in the smaller matricies else: M = matrix(GF(2), size+1) # Restricts the entries to 0 or 1 main_list = set() #print x_cord, y_cord if show_lines: for t in [(-size-1)..size+1]: m= SW_NE(t, xt, yt, start) if m.is_pseudoprime(): main_list.add(m) m= NW_SE(t, xt, yt, start) if m.is_pseudoprime(): main_list.add(m) else: main_list = set(prime_range(end)) #This for loop changes the matrix by spiraling out from the center and changing each entry as it goes. It is faster than the find_xy function above. for num in [start..end]: #print x, "=x y=", y, " num =", num if countx < overcount: if overcount % 2 == 1: x+=1 else: x-=1 countx += 1 elif county < overcount: if overcount % 2 == 1: y+=1 else: y-=1 county += 1 else: overcount += 1 countx=2 county=0 if overcount % 2 == 1: x+=1 else: x-=1 if not invert and num in main_list: if size <= size_limit: M = matrix_morph(M, x, y, num) else: M = matrix_morph(M, x, y, 1) elif invert and num not in main_list: #This does the opposite of the above if statement by changing the matrix only when a number is not in the list of allowable primes if size <= size_limit: M = matrix_morph(M, x, y, num) else: M = matrix_morph(M, x, y, 1) if n != 0: print '(to go from x,y coords to an n, reset by setting n=0)' (x_cord, y_cord) = find_xy(n, start) #print 'if n =', n, 'then (x,y) =', (x_cord, y_cord) print '(x,y) =', (x_cord, y_cord), '<=> n =', find_n(x_cord, y_cord, start) print ' ' print "SW/NE line" if -y_cord<x_cord: print '4*t^2 + 2*t +', -x_cord+y_cord+start else: print '4*t^2 + 2*t +', +x_cord-y_cord+start print "NW/SE line" if x_cord<y_cord: print '4*t^2 +', -x_cord-y_cord+start else: print '4*t^2 + 4*t +', +x_cord+y_cord+start if size <= size_limit: show(M) #Displays the matrix with integer entries else: M.visualize_structure() # Displays the final resulting matrix as a series of pixels (1 <=> pixel on) #matrix_plot(M) }}} {{attachment:SquareSpiral.PNG}} == Prime Spiral - Polar == by David Runde {{{#!sagecell @interact def polar_prime_spiral(start=1, end=2000, show_factors = false, highlight_primes = false, show_curves=true, n = 0): #For more information about the factors in the spiral, visit http://www.dcs.gla.ac.uk/~jhw/spirals/index.html by John Williamson. if start < 1 or end <=start: print "invalid start or end value" if n > end: print "WARNING: n is greater than end value" def f(n): return (sqrt(n)*cos(2*pi*sqrt(n)), sqrt(n)*sin(2*pi*sqrt(n))) list =[] list2=[] if show_factors == false: for i in [start..end]: if i.is_pseudoprime(): list.append(f(i-start+1)) #Primes list else: list2.append(f(i-start+1)) #Composites list P = points(list) R = points(list2, alpha = .1) #Faded Composites else: for i in [start..end]: list.append(disk((f(i-start+1)),0.05*pow(2,len(factor(i))-1), (0,2*pi))) #resizes each of the dots depending of the number of factors of each number if i.is_pseudoprime() and highlight_primes: list2.append(f(i-start+1)) P = plot(list) p_size = 5 #the orange dot size of the prime markers if not highlight_primes: list2 = [(f(n-start+1))] R=points(list2, hue = .1, pointsize = p_size) if n > 0: print 'n =', factor(n) p = 1 #The X which marks the given n W1 = disk((f(n-start+1)), p, (pi/6, 2*pi/6)) W2 = disk((f(n-start+1)), p, (4*pi/6, 5*pi/6)) W3 = disk((f(n-start+1)), p, (7*pi/6, 8*pi/6)) W4 = disk((f(n-start+1)), p, (10*pi/6, 11*pi/6)) Q = plot(W1+W2+W3+W4, alpha = .1) n=n-start+1 #offsets the n for different start values to ensure accurate plotting if show_curves: begin_curve = 0 t = var('t') a=1 b=0 if n > (floor(sqrt(n)))^2 and n <= (floor(sqrt(n)))^2 + floor(sqrt(n)): c = -((floor(sqrt(n)))^2 - n) c2= -((floor(sqrt(n)))^2 + floor(sqrt(n)) - n) else: c = -((ceil(sqrt(n)))^2 - n) c2= -((floor(sqrt(n)))^2 + floor(sqrt(n)) - n) print 'Pink Curve: n^2 +', c print 'Green Curve: n^2 + n +', c2 def g(m): return (a*m^2+b*m+c); def r(m) : return sqrt(g(m)) def theta(m) : return r(m)- m*sqrt(a) S1 = parametric_plot(((r(t))*cos(2*pi*(theta(t))),(r(t))*sin(2*pi*(theta(t)))), begin_curve, ceil(sqrt(end-start)), rgbcolor=hue(0.8), thickness = .2) #Pink Line b=1 c= c2; S2 = parametric_plot(((r(t))*cos(2*pi*(theta(t))),(r(t))*sin(2*pi*(theta(t)))), begin_curve, ceil(sqrt(end-start)), rgbcolor=hue(0.6), thickness = .2) #Green Line show(R+P+S1+S2+Q, aspect_ratio = 1, axes = false) else: show(R+P+Q, aspect_ratio = 1, axes = false) else: show(R+P, aspect_ratio = 1, axes = false) }}} {{attachment:PolarSpiral.PNG}} = Modular Forms = == Computing modular forms == by William Stein {{{#!sagecell @interact def _(N=[1..100], k=selector([2,4,..,12],nrows=1), prec=(3..40), group=[(Gamma0, 'Gamma0'), (Gamma1, 'Gamma1')]): M = CuspForms(group(N),k) print M; print '\n'*3 print "Computing basis...\n\n" if M.dimension() == 0: print "Space has dimension 0" else: prec = max(prec, M.dimension()+1) for f in M.basis(): view(f.q_expansion(prec)) print "\n\n\nDone computing basis." }}} {{attachment:modformbasis.png}} == Computing the cuspidal subgroup == by William Stein {{{#!sagecell html('<h1>Cuspidal Subgroups of Modular Jacobians J0(N)</h1>') @interact def _(N=selector([1..8*13], ncols=8, width=10, default=10)): A = J0(N) print A.cuspidal_subgroup() }}} {{attachment:cuspgroup.png}} == A Charpoly and Hecke Operator Graph == by William Stein {{{#!sagecell # Note -- in Sage-2.10.3; multiedges are missing in plots; loops are missing in 3d plots @interact def f(N = prime_range(11,400), p = selector(prime_range(2,12),nrows=1), three_d = ("Three Dimensional", False)): S = SupersingularModule(N) T = S.hecke_matrix(p) G = DiGraph(T, multiedges=not three_d) if three_d: G.remove_loops() html("<h1>Charpoly and Hecke Graph: Level %s, T_%s</h1>"%(N,p)) show(T.charpoly().factor()) if three_d: show(G.plot3d(), aspect_ratio=[1,1,1]) else: show(G.plot(),figsize=7) }}} {{attachment:heckegraph.png}} = Modular Arithmetic = == Quadratic Residue Table FIXME == by Emily Kirkman {{{#!sagecell from numpy import array as narray @interact def quad_res_plot(first_n_odd_primes = (20,200),display_size=[7..15]): # Compute numpy matrix of legendre symbols r = int(first_n_odd_primes) np = [nth_prime(i+2) for i in range(r)] leg = [[legendre_symbol(np[i], np[j]) for i in range(r)] for j in range(r)] na = narray(leg) for i in range(r): for j in range(r): if na[i][j] == 1 and Mod((np[i]-1)*(np[j]-1)//4,2) == 0: na[i][j] = 2 m = matrix(na) # Define plot structure MP = matrix_plot(m, cmap='Oranges') for i in range(r): if np[-1] < 100: MP += text('%d'%nth_prime(i+2),(-.75,r-i-.5), rgbcolor='black') MP += text('%d'%nth_prime(i+2), (i+.5,r+.5), rgbcolor='black') if len(np) < 75: MP += line([(0,i),(r,i)], rgbcolor='black') MP += line([(i,0),(i,r)], rgbcolor='black') if np[-1] < 100: for i in range(r): # rows for j in range(r): # cols if m[j][i] == 0: MP += text('0',(i+.5,r-j-.5),rgbcolor='black') elif m[j][i] == -1: MP += text('N',(i+.5,r-j-.5),rgbcolor='black') elif m[j][i] == 1: MP += text('A',(i+.5,r-j-.5),rgbcolor='black') elif m[j][i] == 2: MP += text('S',(i+.5,r-j-.5),rgbcolor='black') MP += line([(0,r),(r,r)], rgbcolor='black') MP += line([(r,0),(r,r)], rgbcolor='black') MP += line([(0,0),(r,0)], rgbcolor='black') MP += line([(0,0),(0,r)], rgbcolor='black') if len(np) < 75: MP += text('q',(r/2,r+2), rgbcolor='black', fontsize=15) MP += text('p',(-2.5,r/2), rgbcolor='black', fontsize=15) MP.show(axes=False, ymax=r, figsize=[display_size,display_size]) html('Symmetry of Prime Quadratic Residues mod the first %d odd primes.'%r) }}} {{attachment:quadres.png}} {{attachment:quadresbig.png}} == Cubic Residue Table FIXME == by Emily Kirkman {{{#!sagecell def power_residue_symbol(alpha, p, m): if p.divides(alpha): return 0 if not p.is_prime(): return prod(power_residue_symbol(alpha,ell,m)^e for ell, e in p.factor()) F = p.residue_field() N = p.norm() r = F(alpha)^((N-1)/m) k = p.number_field() for kr in k.roots_of_unity(): if r == F(kr): return kr def cubic_is_primary(n): g = n.gens_reduced()[0] a,b = g.polynomial().coefficients() return Mod(a,3)!=0 and Mod(b,3)==0 from numpy import array as narray @interact def cubic_sym(n=(10..35),display_size=[7..15]): # Compute numpy matrix of primary cubic residue symbols r = n m=3 D.<w> = NumberField(x^2+x+1) it = D.primes_of_degree_one_iter() pp = [] while len(pp) < r: k = it.next() if cubic_is_primary(k): pp.append(k) n = narray([ [ power_residue_symbol(pp[i].gens_reduced()[0], pp[j], m) \ for i in range(r) ] for j in range(r) ]) # Convert to integer matrix for gradient colors for i in range(r): for j in range(r): if n[i][j] == w: n[i][j] = int(-1) elif n[i][j] == w^2: n[i][j] = int(-2) elif n[i][j] == 1: n[i][j] = int(1) m = matrix(n) # Define plot structure MP = matrix_plot(m,cmap="Blues") for i in range(r): MP += line([(0,i),(r,i)], rgbcolor='black') MP += line([(i,0),(i,r)], rgbcolor='black') for j in range(r): if m[i][j] == -2: MP += text('$\omega^2$',(i+.5,r-j-.5),rgbcolor='black') if m[i][j] == -1: MP += text('$\omega $',(i+.5,r-j-.5),rgbcolor='black') if m[i][j] == 0: MP += text('0',(i+.5,r-j-.5),rgbcolor='black') if m[i][j] == 1: MP += text('R',(i+.5,r-j-.5),rgbcolor='white') MP += line([(0,r),(r,r)], rgbcolor='black') MP += line([(r,0),(r,r)], rgbcolor='black') MP += line([(0,0),(r,0)], rgbcolor='black') MP += line([(0,0),(0,r)], rgbcolor='black') MP += text('$ \pi_1$',(r/2,r+2), rgbcolor='black', fontsize=25) MP += text('$ \pi_2$',(-2.5,r/2), rgbcolor='black', fontsize=25) html('Symmetry of Primary Cubic Residues mod ' \ + '%d primary primes in $ \mathbf Z[\omega]$.'%r) MP.show(axes=False, figsize=[display_size,display_size]) }}} {{attachment:cubres.png}} = Cyclotomic Fields = == Gauss and Jacobi Sums in Complex Plane == by Emily Kirkman {{{#!sagecell def jacobi_sum(e,f): # If they are both trivial, return p if e.is_trivial() and f.is_trivial(): return (e.parent()).order() + 1 # If they are inverses of each other, return -e(-1) g = e*f if g.is_trivial(): return -e(-1) # If both are nontrivial, apply mult. formula: elif not e.is_trivial() and not f.is_trivial(): return e.gauss_sum()*f.gauss_sum()/g.gauss_sum() # If exactly one is trivial, return 0 else: return 0 def latex2(e): return latex(list(e.values_on_gens())) def jacobi_plot(p, e_index, f_index, with_text=True): # Set values G = DirichletGroup(p) e = G[e_index] f = G[f_index] ef = e*f js = jacobi_sum(e,f) e_gs = e.gauss_sum() f_gs = f.gauss_sum() ef_gs = (e*f).gauss_sum() # Compute complex coordinates f_pt = list(f.values_on_gens()[0].complex_embedding()) e_pt = list(e.values_on_gens()[0].complex_embedding()) ef_pt = list(ef.values_on_gens()[0].complex_embedding()) f_gs_pt = list(f_gs.complex_embedding()) e_gs_pt = list(e_gs.complex_embedding()) ef_gs_pt = list(ef_gs.complex_embedding()) try: js = int(js) js_pt = [CC(js)] except: js_pt = list(js.complex_embedding()) # Define plot structure S = circle((0,0),1,rgbcolor='yellow') S += line([e_pt,e_gs_pt], rgbcolor='red', thickness=4) S += line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3) S += line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2) S += point(e_pt,pointsize=50, rgbcolor='red') S += point(f_pt,pointsize=50, rgbcolor='blue') S += point(ef_pt,pointsize=50,rgbcolor='purple') S += point(f_gs_pt,pointsize=75, rgbcolor='black') S += point(e_gs_pt,pointsize=75, rgbcolor='black') S += point(ef_gs_pt,pointsize=75, rgbcolor='black') S += point(js_pt,pointsize=100,rgbcolor='green') if with_text: S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)), (3,2.5),fontsize=15, rgbcolor='black') else: html('$$J(%s,%s) = %s$$'%(latex2(e),latex2(f),latex(js))) return S @interact def single_jacobi_plot(p=prime_range(3,100), e_range=(0..100), f_range=(0..100)): e_index = floor((p-2)*e_range/100) f_index = floor((p-2)*f_range/100) S = jacobi_plot(p,e_index,f_index,with_text=False) S.show(aspect_ratio=1) }}} {{attachment:jacobising.png}} == Exhaustive Jacobi Plotter == by Emily Kirkman {{{#!sagecell def jacobi_sum(e,f): # If they are both trivial, return p if e.is_trivial() and f.is_trivial(): return (e.parent()).order() + 1 # If they are inverses of each other, return -e(-1) g = e*f if g.is_trivial(): return -e(-1) # If both are nontrivial, apply mult. formula: elif not e.is_trivial() and not f.is_trivial(): return e.gauss_sum()*f.gauss_sum()/g.gauss_sum() # If exactly one is trivial, return 0 else: return 0 def latex2(e): return latex(list(e.values_on_gens())) def jacobi_plot(p, e_index, f_index, with_text=True): # Set values G = DirichletGroup(p) e = G[e_index] f = G[f_index] ef = e*f js = jacobi_sum(e,f) e_gs = e.gauss_sum() f_gs = f.gauss_sum() ef_gs = (e*f).gauss_sum() # Compute complex coordinates f_pt = list(f.values_on_gens()[0].complex_embedding()) e_pt = list(e.values_on_gens()[0].complex_embedding()) ef_pt = list(ef.values_on_gens()[0].complex_embedding()) f_gs_pt = list(f_gs.complex_embedding()) e_gs_pt = list(e_gs.complex_embedding()) ef_gs_pt = list(ef_gs.complex_embedding()) try: js = int(js) js_pt = [CC(js)] except: js_pt = list(js.complex_embedding()) # Define plot structure S = circle((0,0),1,rgbcolor='yellow') S += line([e_pt,e_gs_pt], rgbcolor='red', thickness=4) S += line([f_pt,f_gs_pt], rgbcolor='blue', thickness=3) S += line([ef_pt,ef_gs_pt], rgbcolor='purple',thickness=2) S += point(e_pt,pointsize=50, rgbcolor='red') S += point(f_pt,pointsize=50, rgbcolor='blue') S += point(ef_pt,pointsize=50,rgbcolor='purple') S += point(f_gs_pt,pointsize=75, rgbcolor='black') S += point(e_gs_pt,pointsize=75, rgbcolor='black') S += point(ef_gs_pt,pointsize=75, rgbcolor='black') S += point(js_pt,pointsize=100,rgbcolor='green') if with_text: S += text('$J(%s,%s) = %s$'%(latex2(e),latex2(f),latex(js)), (3,2.5),fontsize=15, rgbcolor='black') else: html('$$J(%s,%s) = %s$$'%(latex2(e),latex2(f),latex(js))) return S @interact def exhaustive_jacobi_plot(p=prime_range(3,8)): ga = [jacobi_plot(p,i,j) for i in range(p-1) for j in range(p-1)[i:]] for i in range(len(ga)): ga[i].save('j%d.png'%i,figsize=4,aspect_ratio=1, xmin=-2.5,xmax=5, ymin=-2.5, ymax=2.5) # Since p is odd, will have n = p-1 even. So 1+2+...+n = (n/2)*(n+1). # We divide this by rows of 2. rows = ceil(p*(p-1)/4) s='<table bgcolor=lightgrey cellpadding=2>' for i in range(rows): s+='<tr><td align="center"><img src="cell://j%d.png"></td>'%(2*i) s+='<td align="center"><img src="cell://j%d.png"></td></tr>'%(2*i+1) s+='</table>' html(s)}}} {{attachment:jacobiexh.png}} = Elliptic Curves = == Adding points on an elliptic curve == by David Møller Hansen {{{#!sagecell def point_txt(P,name,rgbcolor): if (P.xy()[1]) < 0: r = text(name,[float(P.xy()[0]),float(P.xy()[1])-1],rgbcolor=rgbcolor) elif P.xy()[1] == 0: r = text(name,[float(P.xy()[0]),float(P.xy()[1])+1],rgbcolor=rgbcolor) else: r = text(name,[float(P.xy()[0]),float(P.xy()[1])+1],rgbcolor=rgbcolor) return r E = EllipticCurve('37a') list_of_points = E.integral_points() html("Graphical addition of two points $P$ and $Q$ on the curve $ E: %s $"%latex(E)) def line_from_curve_points(E,P,Q,style='-',rgb=(1,0,0),length=25): """ P,Q two points on an elliptic curve. Output is a graphic representation of the straight line intersecting with P,Q. """ # The function tangent to P=Q on E if P == Q: if P[2]==0: return line([(1,-length),(1,length)],linestyle=style,rgbcolor=rgb) else: # Compute slope of the curve E in P l=-(3*P[0]^2 + 2*E.a2()*P[0] + E.a4() - E.a1()*P[1])/((-2)*P[1] - E.a1()*P[0] - E.a3()) f(x) = l * (x - P[0]) + P[1] return plot(f(x),-length,length,linestyle=style,rgbcolor=rgb) # Trivial case of P != R where P=O or R=O then we get the vertical line from the other point elif P[2] == 0: return line([(Q[0],-length),(Q[0],length)],linestyle=style,rgbcolor=rgb) elif Q[2] == 0: return line([(P[0],-length),(P[0],length)],linestyle=style,rgbcolor=rgb) # Non trivial case where P != R else: # Case where x_1 = x_2 return vertical line evaluated in Q if P[0] == Q[0]: return line([(P[0],-length),(P[0],length)],linestyle=style,rgbcolor=rgb) #Case where x_1 != x_2 return line trough P,R evaluated in Q" l=(Q[1]-P[1])/(Q[0]-P[0]) f(x) = l * (x - P[0]) + P[1] return plot(f(x),-length,length,linestyle=style,rgbcolor=rgb) @interact def _(P=selector(list_of_points,label='Point P'),Q=selector(list_of_points,label='Point Q'), marked_points = checkbox(default=True,label = 'Points'), Lines = selector([0..2],nrows=1), Axes=True): curve = E.plot(rgbcolor = (0,0,1),xmin=-5,xmax=5,plot_points=300) R = P + Q Rneg = -R l1 = line_from_curve_points(E,P,Q) l2 = line_from_curve_points(E,R,Rneg,style='--') p1 = plot(P,rgbcolor=(1,0,0),pointsize=40) p2 = plot(Q,rgbcolor=(1,0,0),pointsize=40) p3 = plot(R,rgbcolor=(1,0,0),pointsize=40) p4 = plot(Rneg,rgbcolor=(1,0,0),pointsize=40) textp1 = point_txt(P,"$P$",rgbcolor=(0,0,0)) textp2 = point_txt(Q,"$Q$",rgbcolor=(0,0,0)) textp3 = point_txt(R,"$P+Q$",rgbcolor=(0,0,0)) if Lines==0: g=curve elif Lines ==1: g=curve+l1 elif Lines == 2: g=curve+l1+l2 if marked_points: g=g+p1+p2+p3+p4 if P != Q: g=g+textp1+textp2+textp3 else: g=g+textp1+textp3 g.axes_range(xmin=-5,xmax=5,ymin=-13,ymax=13) show(g,axes = Axes) }}} {{attachment:PointAddEllipticCurve.png}} == Plotting an elliptic curve over a finite field == {{{#!sagecell E = EllipticCurve('37a') @interact def _(p=slider(prime_range(1000), default=389)): show(E) print "p = %s"%p show(E.change_ring(GF(p)).plot(),xmin=0,ymin=0) }}} {{attachment:ellffplot.png}} = Cryptography = == The Diffie-Hellman Key Exchange Protocol == by Timothy Clemans and William Stein {{{#!sagecell @interact def diffie_hellman(bits=slider(8, 513, 4, 8, 'Number of bits', False), button=selector(["Show new example"],label='',buttons=True)): maxp = 2 ^ bits p = random_prime(maxp) k = GF(p) if bits > 100: g = k(2) else: g = k.multiplicative_generator() a = ZZ.random_element(10, maxp) b = ZZ.random_element(10, maxp) html(""" <style> .gamodp, .gbmodp { color:#000; padding:5px } .gamodp { background:#846FD8 } .gbmodp { background:#FFFC73 } .dhsame { color:#000; font-weight:bold } </style> <h2 style="color:#000;font-family:Arial, Helvetica, sans-serif">%s-Bit Diffie-Hellman Key Exchange</h2> <ol style="color:#000;font-family:Arial, Helvetica, sans-serif"> <li>Alice and Bob agree to use the prime number p = %s and base g = %s.</li> <li>Alice chooses the secret integer a = %s, then sends Bob (<span class="gamodp">g<sup>a</sup> mod p</span>):<br/>%s<sup>%s</sup> mod %s = <span class="gamodp">%s</span>.</li> <li>Bob chooses the secret integer b=%s, then sends Alice (<span class="gbmodp">g<sup>b</sup> mod p</span>):<br/>%s<sup>%s</sup> mod %s = <span class="gbmodp">%s</span>.</li> <li>Alice computes (<span class="gbmodp">g<sup>b</sup> mod p</span>)<sup>a</sup> mod p:<br/>%s<sup>%s</sup> mod %s = <span class="dhsame">%s</span>.</li> <li>Bob computes (<span class="gamodp">g<sup>a</sup> mod p</span>)<sup>b</sup> mod p:<br/>%s<sup>%s</sup> mod %s = <span class="dhsame">%s</span>.</li> </ol> """ % (bits, p, g, a, g, a, p, (g^a), b, g, b, p, (g^b), (g^b), a, p, (g^ b)^a, g^a, b, p, (g^a)^b)) }}} {{attachment:dh.png}} = Other = == Continued Fraction Plotter == by William Stein {{{#!sagecell @interact def _(number=e, ymax=selector([5,20,..,400],nrows=2), clr=Color('purple'), prec=[500,1000,..,5000]): c = list(continued_fraction(RealField(prec)(number))); print c show(line([(i,z) for i, z in enumerate(c)],rgbcolor=clr),ymax=ymax,figsize=[10,2]) }}} {{attachment:contfracplot.png}} == Computing Generalized Bernoulli Numbers == |
| Line 75: | Line 824: |
| {{{ | {{{#!sagecell |
| Line 91: | Line 840: |
| attachment:bernoulli.png === Fundamental Domains of SL_2(ZZ) === |
{{attachment:bernoulli.png}} == Fundamental Domains of SL_2(ZZ) == |
| Line 96: | Line 845: |
| {{{ | {{{#!sagecell |
| Line 104: | Line 853: |
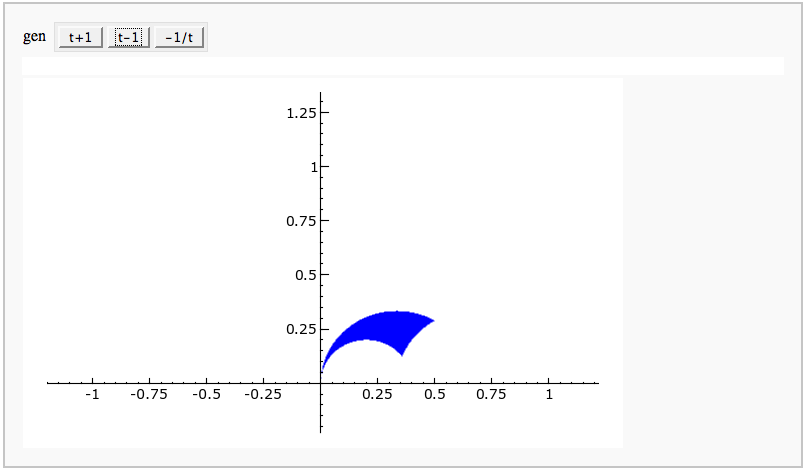
| def _(gen = selector(['t+1', 't-1', '-1/t'], nrows=1)): | def _(gen = selector(['t+1', 't-1', '-1/t'], buttons=True,nrows=1)): |
| Line 121: | Line 870: |
| attachment:fund_domain.png === Computing modular forms === by William Stein {{{ j = 0 @interact def _(N=[1..100], k=selector([2,4,..,12],nrows=1), prec=(3..40), group=[(Gamma0, 'Gamma0'), (Gamma1, 'Gamma1')]): M = CuspForms(group(N),k) print j; global j; j += 1 print M; print '\n'*3 print "Computing basis...\n\n" if M.dimension() == 0: print "Space has dimension 0" else: prec = max(prec, M.dimension()+1) for f in M.basis(): view(f.q_expansion(prec)) print "\n\n\nDone computing basis." }}} attachment:modformbasis.png === Computing the cuspidal subgroup === by William Stein {{{ html('<h1>Cuspidal Subgroups of Modular Jacobians J0(N)</h1>') @interact def _(N=selector([1..8*13], ncols=8, width=10, default=10)): A = J0(N) print A.cuspidal_subgroup() }}} attachment:cuspgroup.png === A Charpoly and Hecke Operator Graph === by William Stein {{{ # Note -- in Sage-2.10.3; multiedges are missing in plots; loops are missing in 3d plots @interact def f(N = prime_range(11,400), p = selector(prime_range(2,12),nrows=1), three_d = ("Three Dimensional", False)): S = SupersingularModule(N) T = S.hecke_matrix(p) G = Graph(T, multiedges=True, loops=not three_d) html("<h1>Charpoly and Hecke Graph: Level %s, T_%s</h1>"%(N,p)) show(T.charpoly().factor()) if three_d: show(G.plot3d(), aspect_ratio=[1,1,1]) else: show(G.plot(),figsize=7) }}} attachment:heckegraph.png === Demonstrating the Diffie-Hellman Key Exchange Protocol === by Timothy Clemans (refereed by William Stein) {{{ @interact def diffie_hellman(button=selector(["New example"],label='',buttons=True), bits=("Number of bits of prime", (8,12,..512))): maxp = 2^bits p = random_prime(maxp) k = GF(p) if bits>100: g = k(2) else: g = k.multiplicative_generator() a = ZZ.random_element(10, maxp) b = ZZ.random_element(10, maxp) print """ <html> <style> .gamodp { background:yellow } .gbmodp { background:orange } .dhsame { color:green; font-weight:bold } </style> <h2>%s-Bit Diffie-Hellman Key Exchange</h2> <ol style="color:#000;font:12px Arial, Helvetica, sans-serif"> <li>Alice and Bob agree to use the prime number p=%s and base g=%s.</li> <li>Alice chooses the secret integer a=%s, then sends Bob (<span class="gamodp">g<sup>a</sup> mod p</span>):<br/>%s<sup>%s</sup> mod %s = <span class="gamodp">%s</span>.</li> <li>Bob chooses the secret integer b=%s, then sends Alice (<span class="gbmodp">g<sup>b</sup> mod p</span>):<br/>%s<sup>%s</sup> mod %s = <span class="gbmodp">%s</span>.</li> <li>Alice computes (<span class="gbmodp">g<sup>b</sup> mod p</span>)<sup>a</sup> mod p:<br/>%s<sup>%s</sup> mod %s = <span class="dhsame">%s</span>.</li> <li>Bob computes (<span class="gamodp">g<sup>a</sup> mod p</span>)<sup>b</sup> mod p:<br/>%s<sup>%s</sup> mod %s = <span class="dhsame">%s</span>.</li> </ol></html> """ % (bits, p, g, a, g, a, p, (g^a), b, g, b, p, (g^b), (g^b), a, p, (g^ b)^a, g^a, b, p, (g^a)^b) }}} attachment:dh.png === Plotting an elliptic curve over a finite field === {{{ E = EllipticCurve('37a') @interact def _(p=slider(prime_range(1000), default=389)): show(E) print "p = %s"%p show(E.change_ring(GF(p)).plot(),xmin=0,ymin=0) }}} attachment:ellffplot.png |
{{attachment:fund_domain.png}} = Multiple Zeta Values = by Akhilesh P. == Computing Multiple Zeta values == {{{#!sagecell R=RealField(10) @interact def _( weight=(7,(3..10))): n=weight a=[0 for i in range(n-1)] a.append(1) @interact def _(v=('word', input_grid(1, n, default=[a], to_value=lambda x: vector(flatten(x)))), accuracy=(100..100000)): D=accuracy a=[v[i] for i in range(len(v))] DD=int(3.321928*D)+int(R(log(3.321928*D))/R(log(10)))+4 RIF=RealIntervalField(DD) def Li(word): n=int(DD*log(10)/log(2))+1 B=[] L=[] S=[] count=-1 k=len(word) for i in range(k): B.append(RIF('0')) L.append(RIF('0')) if(word[i]==1 and i<k-1): S.append(RIF('0')) count=count+1 T=RIF('1') for m in range(n): T=T/2 B[k-1]=RIF('1')/(m+1) j=count for i in range(k-2,-1,-1): if(word[i]==0): B[i]=B[i+1]/(m+1) elif(word[i]==1): B[i]=S[j]/(m+1) S[j]=S[j]+B[i+1] j=j-1 L[i]=T*B[i]+L[i] L[k-1]=T*B[k-1]+L[k-1] return(L) def dual(a): b=list() b=a b=b[::-1] for i in range(len(b)): b[i]=1-b[i] return(b) def zeta(a): b=dual(a) l1=Li(a)+[1] l2=Li(b)+[1] Z=RIF('0') for i in range(len(l1)): Z=Z+l1[i]*l2[len(a)-i] return(Z) print zeta(a) }}} |
Contents
Integer Factorization
Divisibility Poset
by William Stein
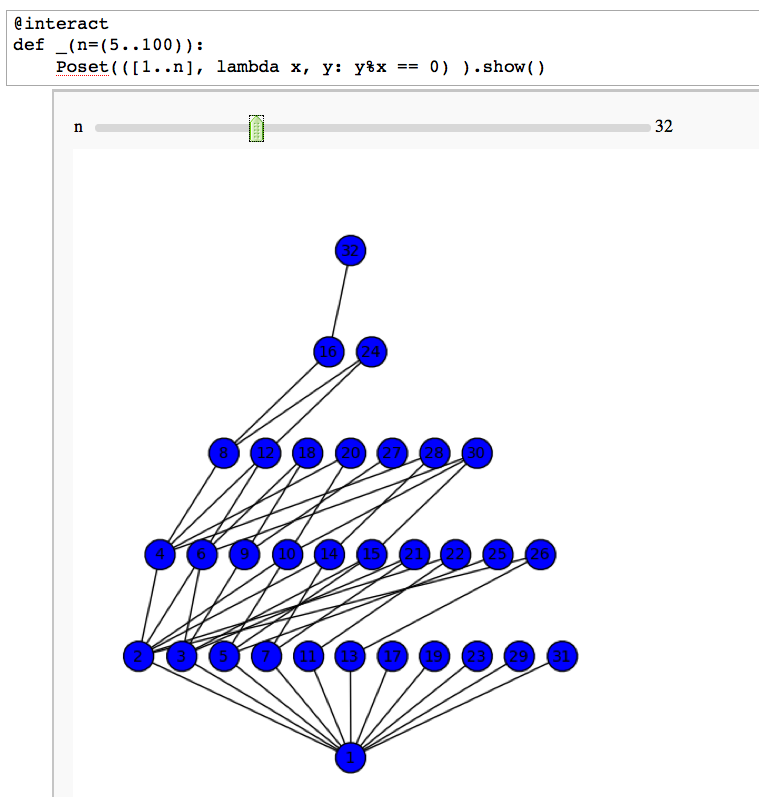
Factor Trees
by William Stein
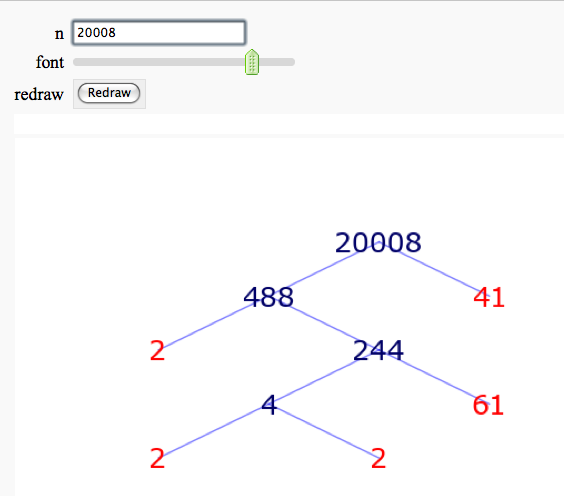
More complicated demonstration using Mathematica: http://demonstrations.wolfram.com/FactorTrees/
Factoring an Integer
by Timothy Clemans
Sage implementation of the Mathematica demonstration of the same name. http://demonstrations.wolfram.com/FactoringAnInteger/
Prime Numbers
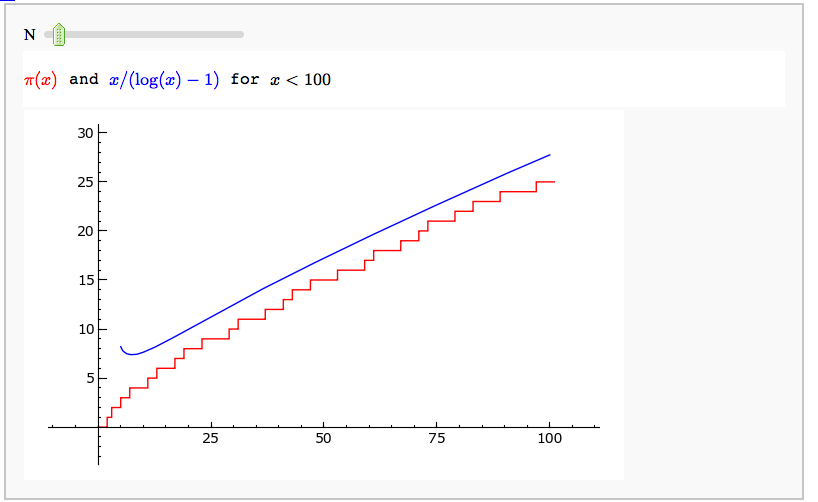
Illustrating the prime number theorem
by William Stein
Prime Spiral - Square FIXME
by David Runde
Prime Spiral - Polar
by David Runde
Modular Forms
Computing modular forms
by William Stein
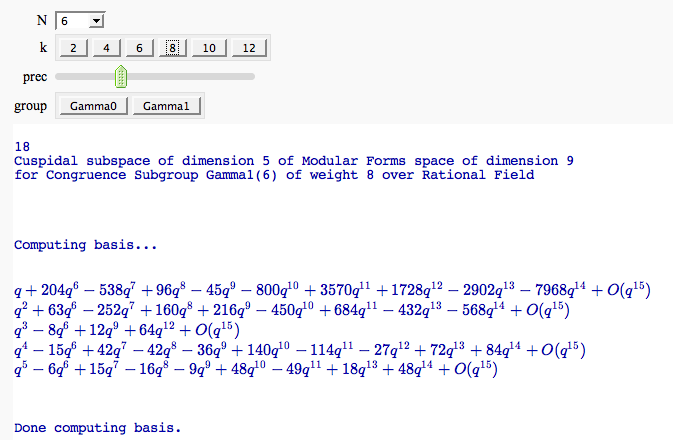
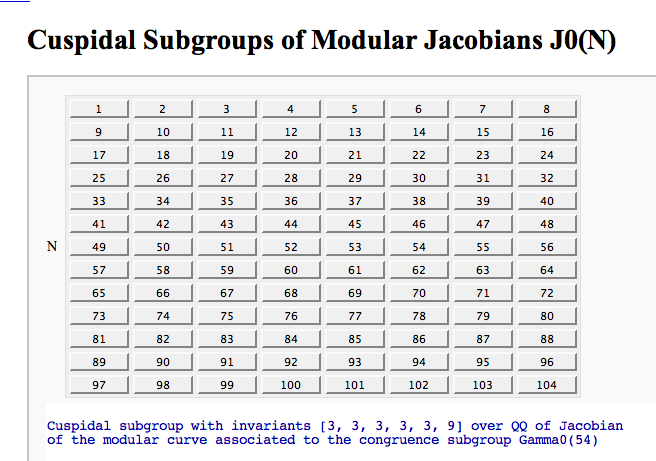
Computing the cuspidal subgroup
by William Stein
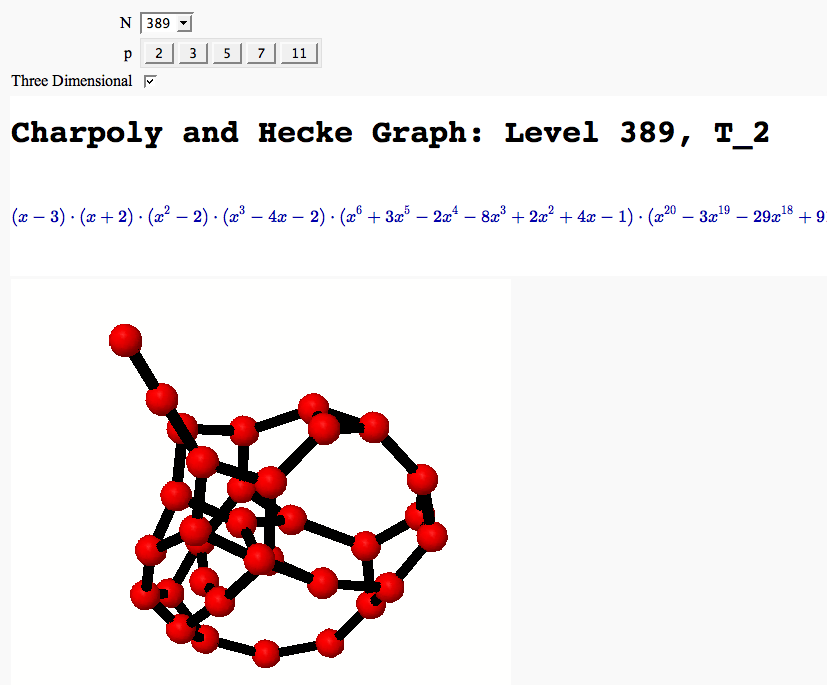
A Charpoly and Hecke Operator Graph
by William Stein
Modular Arithmetic
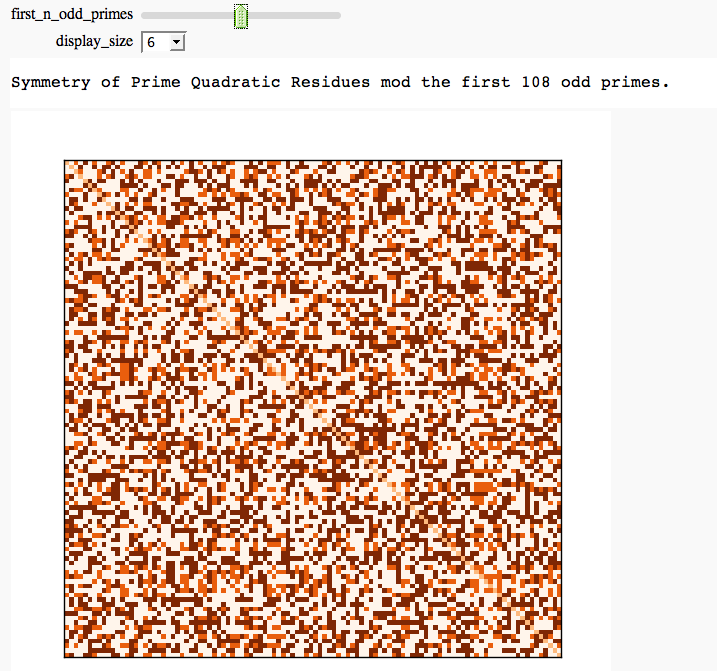
Quadratic Residue Table FIXME
by Emily Kirkman

Cubic Residue Table FIXME
by Emily Kirkman

Cyclotomic Fields
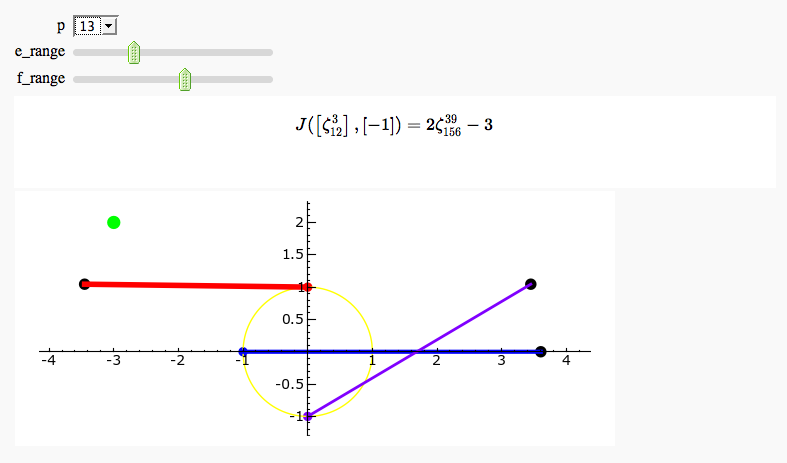
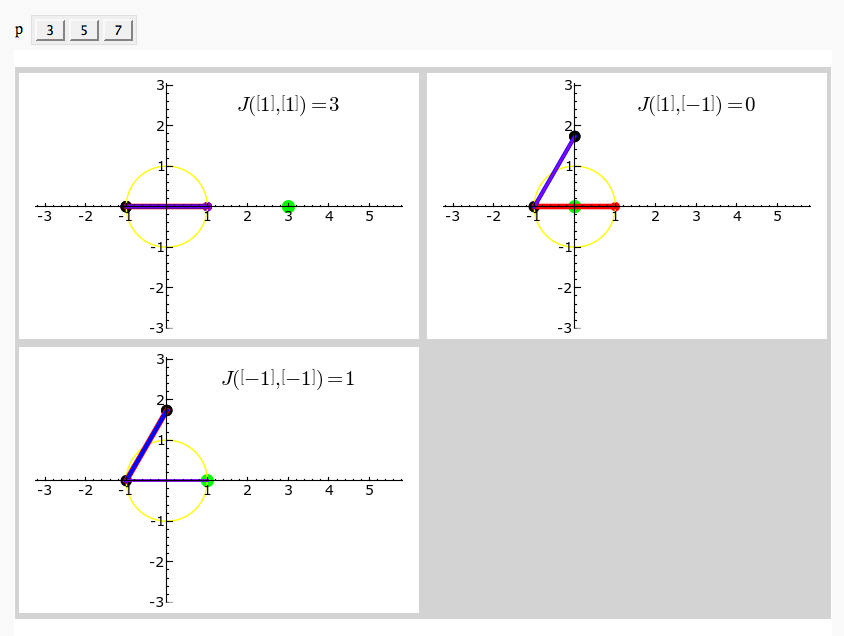
Gauss and Jacobi Sums in Complex Plane
by Emily Kirkman
Exhaustive Jacobi Plotter
by Emily Kirkman
Elliptic Curves
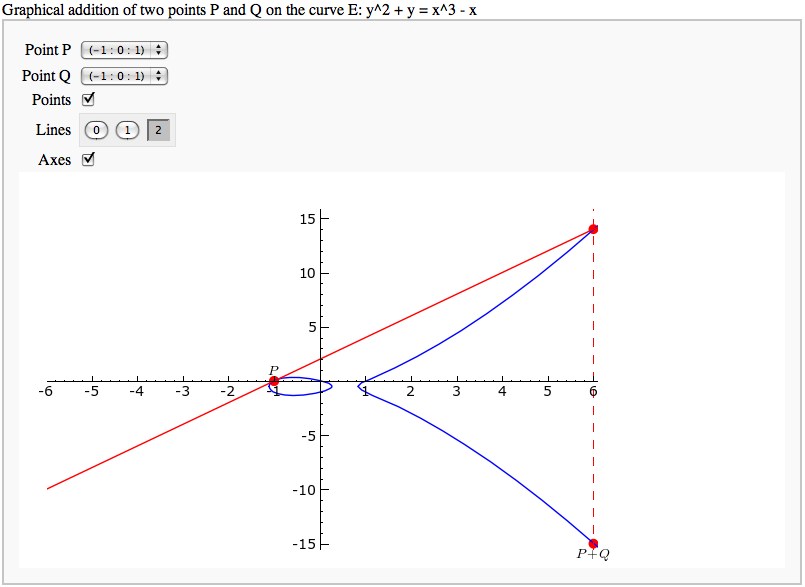
Adding points on an elliptic curve
by David Møller Hansen
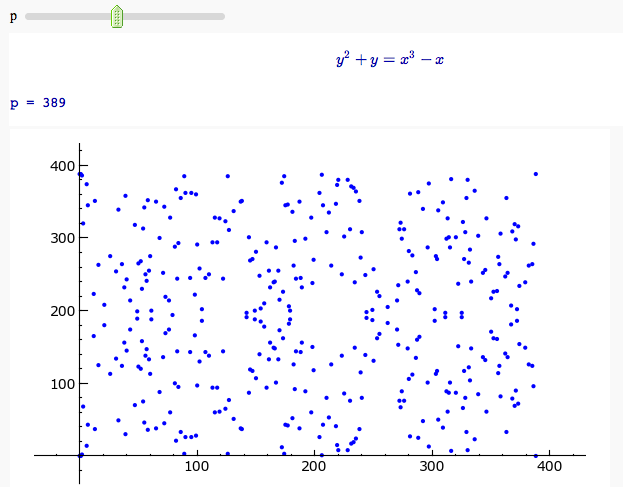
Plotting an elliptic curve over a finite field
Cryptography
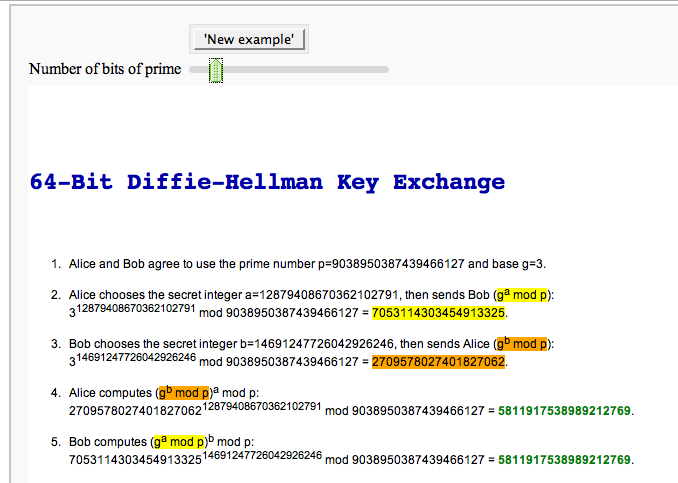
The Diffie-Hellman Key Exchange Protocol
by Timothy Clemans and William Stein
Other
Continued Fraction Plotter
by William Stein
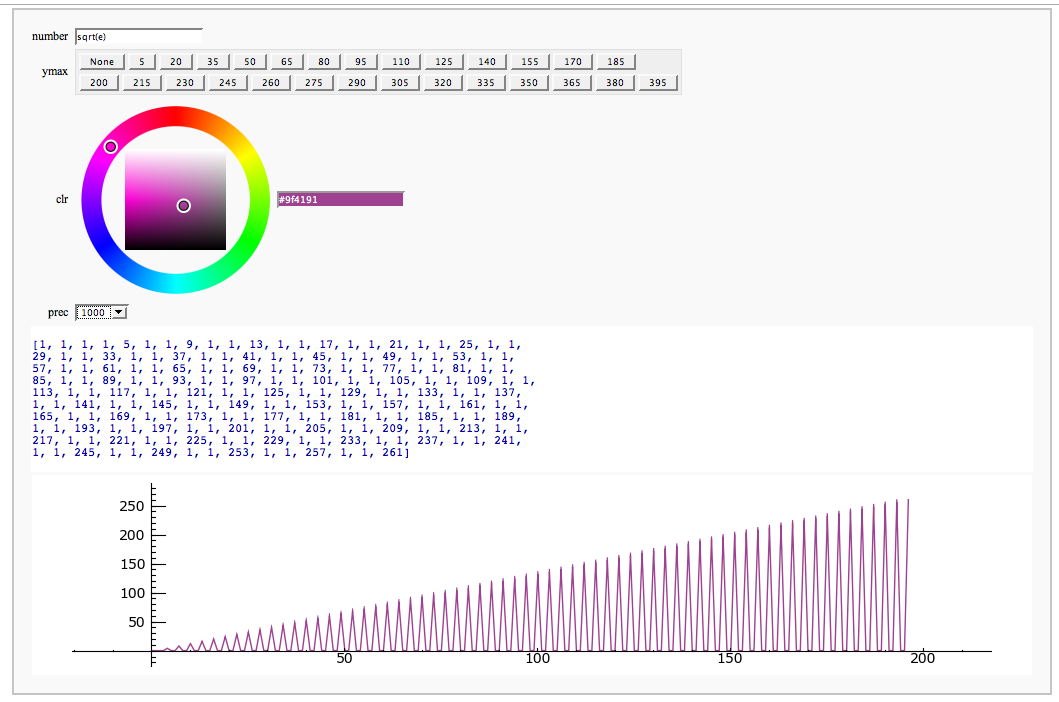
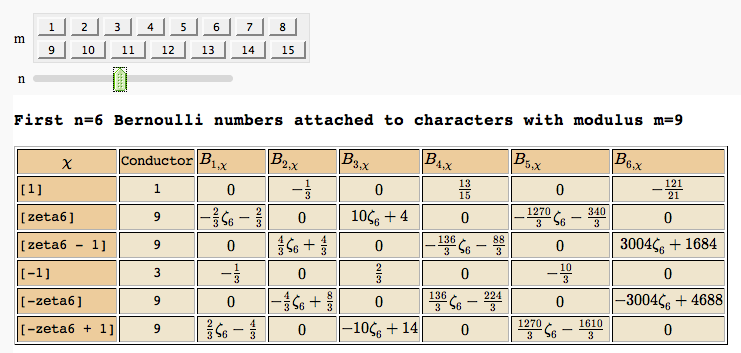
Computing Generalized Bernoulli Numbers
by William Stein (Sage-2.10.3)
Fundamental Domains of SL_2(ZZ)
by Robert Miller
Multiple Zeta Values
by Akhilesh P.
Computing Multiple Zeta values
