Sage Interactions - Graphics
goto interact main page
Contents
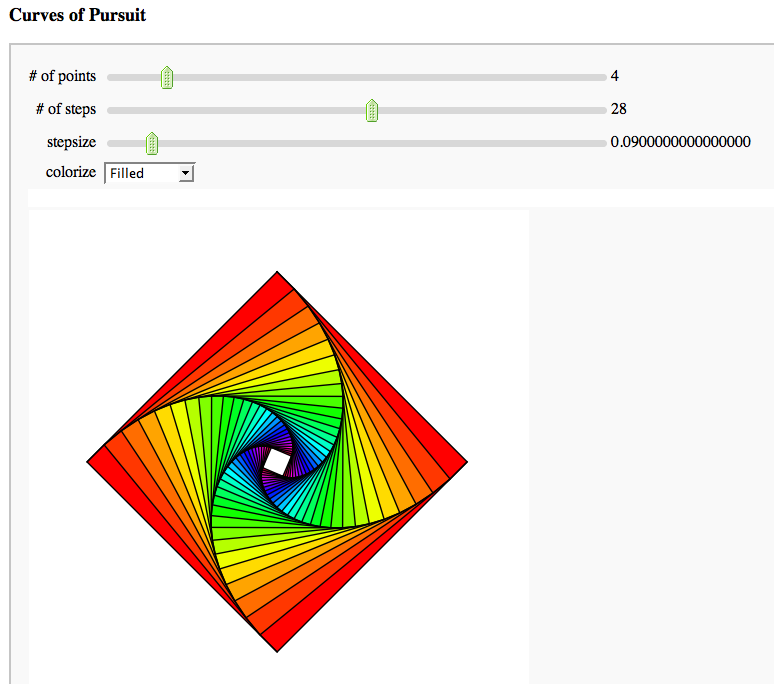
Curves of Pursuit
by Marshall Hampton. {{{#!sagecell#!sagecell npi = RDF(pi) from math import cos,sin def rot(t):
return matrix(cos(t),sin(t)],[-sin(t),cos(t))
def pursuit(n,x0,y0,lamb,steps = 100, threshold = .01):
paths = [x0,y0] for i in range(1,n):
- rx,ry = list(rot(2*npi*i/n)*vector([x0,y0]))
paths.append(rx,ry)
diffs = oldpath[(j+1)%n][0]-oldpath[j][0],oldpath[(j+1)%n][1]-oldpath[j][1 for j in range(n)] npath = oldpath[j][0]+lamb*diffs[j][0],oldpath[j][1]+lamb*diffs[j][1 for j in range(n)] for j in range(n):
- paths[j].append(npath[j])
- rx,ry = list(rot(2*npi*i/n)*vector([x0,y0]))
html('<h3>Curves of Pursuit</h3>') @interact def curves_of_pursuit(n = slider([2..20],default = 5, label="# of points"),steps = slider([floor(1.4^i) for i in range(2,18)],default = 10, label="# of steps"), stepsize = slider(srange(.01,1,.01),default = .2, label="stepsize"), colorize = selector(['BW','Line color', 'Filled'],default = 'BW')):
- outpaths = pursuit(n,0,1,stepsize, steps = steps) mcolor = (0,0,0) outer = line([q[0] for q in outpaths]+[outpaths[0][0]], rgbcolor = mcolor) polys = Graphics() if colorize=='Line color':
- colors = [hue(j/steps,1,1) for j in range(len(outpaths[0]))]
- colors = [(0,0,0) for j in range(len(outpaths[0]))]
- colors = [hue(j/steps,1,1) for j in range(len(outpaths[0]))] polys = sum([polygon([outpaths[(i+1)%n][j+1],outpaths[(i+1)%n][j], outpaths[i][j+1]], rgbcolor = colors[j]) for i in range(n) for j in range(len(outpaths[0])-1)]) #polys = polys[0] colors = [(0,0,0) for j in range(len(outpaths[0]))]
}}} 
Catalog of 3D Parametric Plots
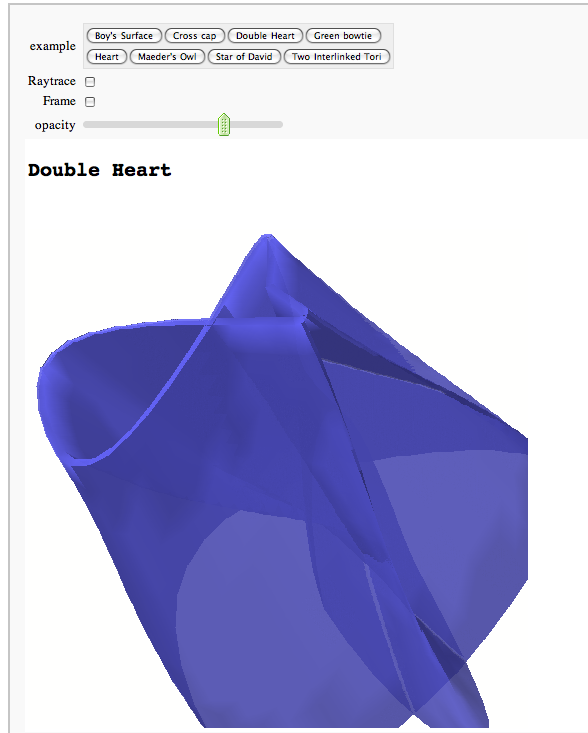
Interactive rotatable raytracing with Tachyon3d
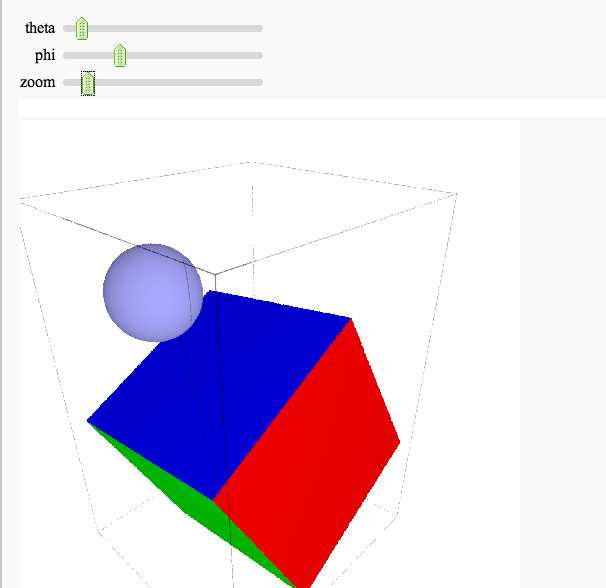
Interactive 3d plotting

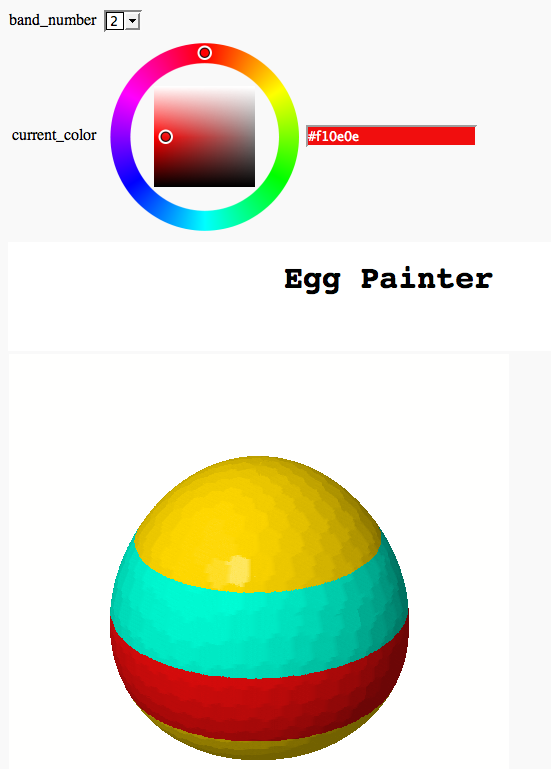
Somewhat Silly Egg Painter
by Marshall Hampton (refereed by William Stein)
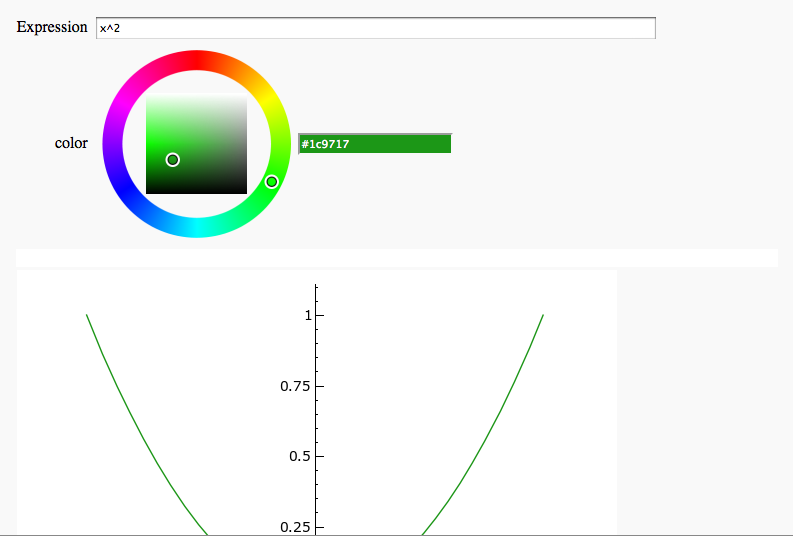
Plot Coloring
by Timothy Clemans
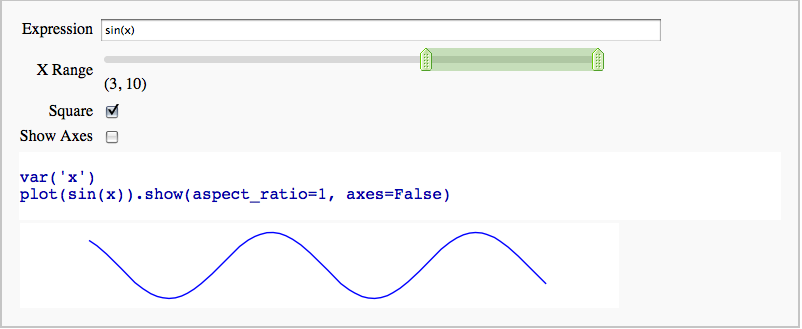
Interactive 2D Plotting
by Timothy Clemans
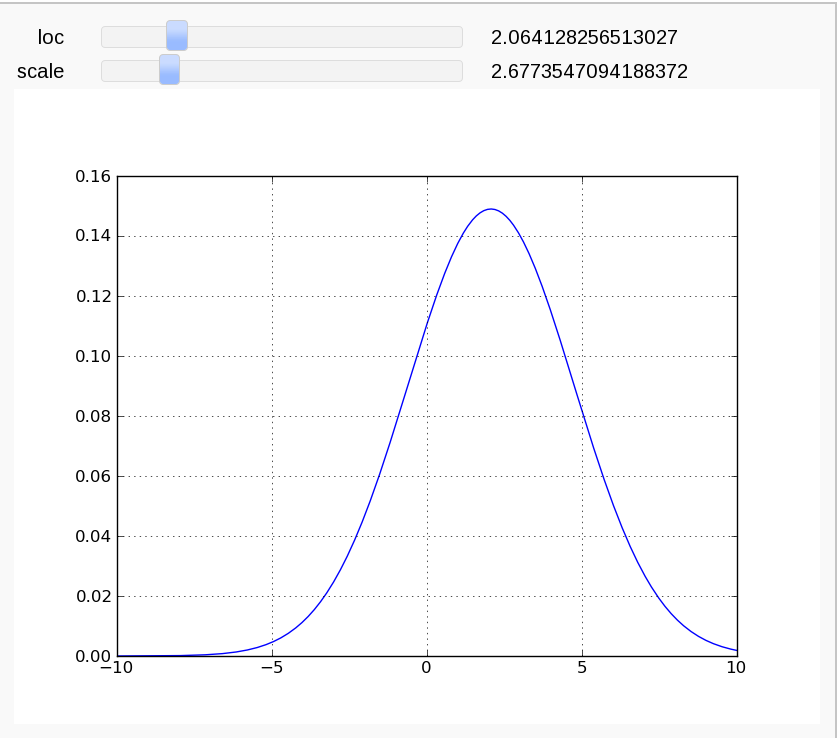
Interact with matplotlib
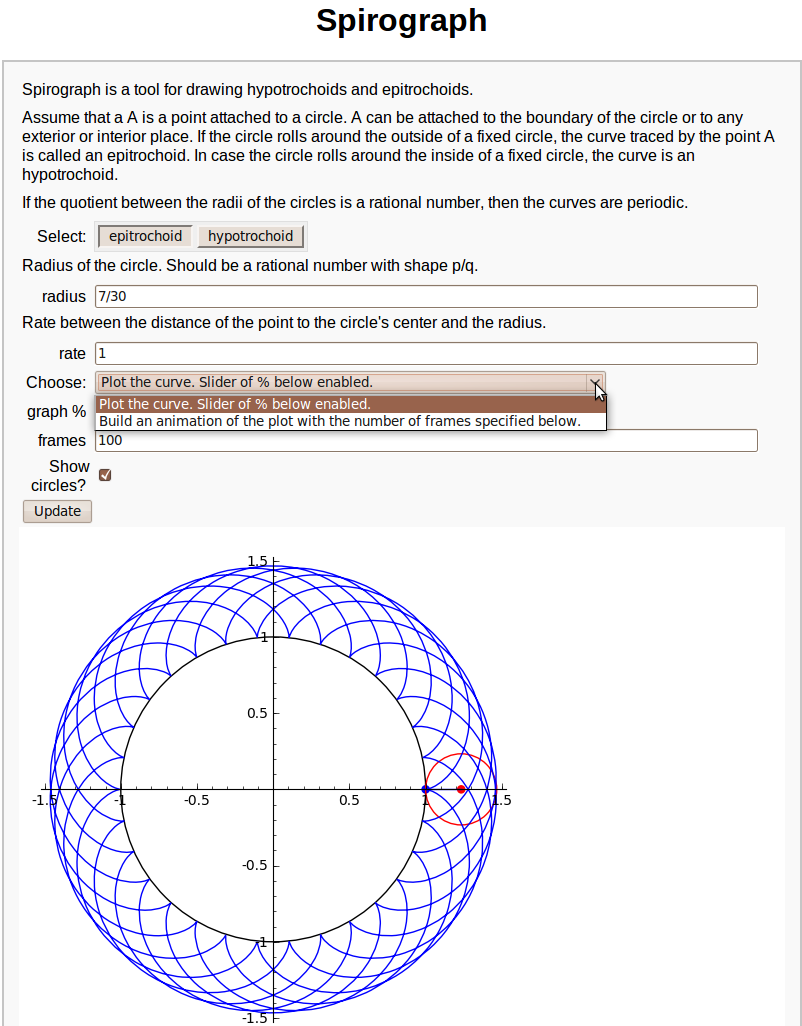
Spirograph