|
Size: 14042
Comment:
|
Size: 14052
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 163: | Line 163: |
| }}} {{{ |
|
| Line 185: | Line 187: |
| == Interactive 2d Plotting == | == Interactive 2D Plotting == |
Sage Interactions - Graphics
goto interact main page
Contents
Curves of Pursuit
by Marshall Hampton.
npi = RDF(pi)
from math import cos,sin
def rot(t):
return matrix([[cos(t),sin(t)],[-sin(t),cos(t)]])
def pursuit(n,x0,y0,lamb,steps = 100, threshold = .01):
paths = [[[x0,y0]]]
for i in range(1,n):
rx,ry = list(rot(2*npi*i/n)*vector([x0,y0]))
paths.append([[rx,ry]])
oldpath = [x[-1] for x in paths]
for q in range(steps):
diffs = [[oldpath[(j+1)%n][0]-oldpath[j][0],oldpath[(j+1)%n][1]-oldpath[j][1]] for j in range(n)]
npath = [[oldpath[j][0]+lamb*diffs[j][0],oldpath[j][1]+lamb*diffs[j][1]] for j in range(n)]
for j in range(n):
paths[j].append(npath[j])
oldpath = npath
return paths
html('<h3>Curves of Pursuit</h3>')
@interact
def curves_of_pursuit(n = slider([2..20],default = 5, label="# of points"),steps = slider([floor(1.4^i) for i in range(2,18)],default = 10, label="# of steps"), stepsize = slider(srange(.01,1,.01),default = .2, label="stepsize"), colorize = selector(['BW','Line color', 'Filled'],default = 'BW')):
outpaths = pursuit(n,0,1,stepsize, steps = steps)
mcolor = (0,0,0)
outer = line([q[0] for q in outpaths]+[outpaths[0][0]], rgbcolor = mcolor)
polys = Graphics()
if colorize=='Line color':
colors = [hue(j/steps,1,1) for j in range(len(outpaths[0]))]
elif colorize == 'BW':
colors = [(0,0,0) for j in range(len(outpaths[0]))]
else:
colors = [hue(j/steps,1,1) for j in range(len(outpaths[0]))]
polys = sum([polygon([outpaths[(i+1)%n][j+1],outpaths[(i+1)%n][j], outpaths[i][j+1]], rgbcolor = colors[j]) for i in range(n) for j in range(len(outpaths[0])-1)])
#polys = polys[0]
colors = [(0,0,0) for j in range(len(outpaths[0]))]
nested = sum([line([q[j] for q in outpaths]+[outpaths[0][j]], rgbcolor = colors[j]) for j in range(len(outpaths[0]))])
lpaths = [line(x, rgbcolor = mcolor) for x in outpaths]
show(sum(lpaths)+nested+polys, axes = False, figsize = [5,5], xmin = -1, xmax = 1, ymin = -1, ymax =1)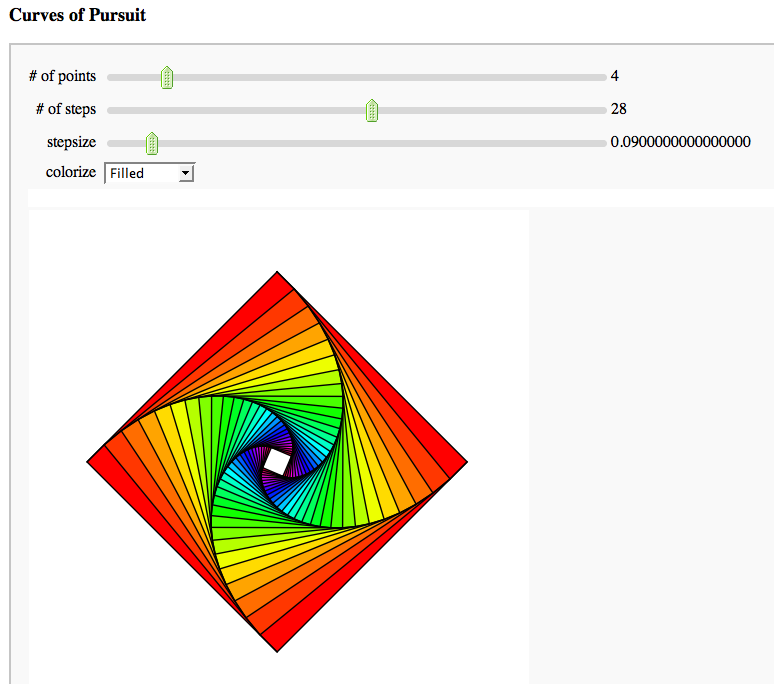
Catalog of 3D Parametric Plots
var('u,v')
plots = ['Two Interlinked Tori', 'Star of David', 'Double Heart',
'Heart', 'Green bowtie', "Boy's Surface", "Maeder's Owl",
'Cross cap']
plots.sort()
@interact
def _(example=selector(plots, buttons=True, nrows=2),
tachyon=("Raytrace", False), frame = ('Frame', False),
opacity=(1,(0.1,1))):
url = ''
if example == 'Two Interlinked Tori':
f1 = (4+(3+cos(v))*sin(u), 4+(3+cos(v))*cos(u), 4+sin(v))
f2 = (8+(3+cos(v))*cos(u), 3+sin(v), 4+(3+cos(v))*sin(u))
p1 = parametric_plot3d(f1, (u,0,2*pi), (v,0,2*pi), color="red", opacity=opacity)
p2 = parametric_plot3d(f2, (u,0,2*pi), (v,0,2*pi), color="blue",opacity=opacity)
P = p1 + p2
elif example == 'Star of David':
f_x = cos(u)*cos(v)*(abs(cos(3*v/4))^500 + abs(sin(3*v/4))^500)^(-1/260)*(abs(cos(4*u/4))^200 + abs(sin(4*u/4))^200)^(-1/200)
f_y = cos(u)*sin(v)*(abs(cos(3*v/4))^500 + abs(sin(3*v/4))^500)^(-1/260)*(abs(cos(4*u/4))^200 + abs(sin(4*u/4))^200)^(-1/200)
f_z = sin(u)*(abs(cos(4*u/4))^200 + abs(sin(4*u/4))^200)^(-1/200)
P = parametric_plot3d([f_x, f_y, f_z], (u, -pi, pi), (v, 0, 2*pi),opacity=opacity)
elif example == 'Double Heart':
f_x = ( abs(v) - abs(u) - abs(tanh((1/sqrt(2))*u)/(1/sqrt(2))) + abs(tanh((1/sqrt(2))*v)/(1/sqrt(2))) )*sin(v)
f_y = ( abs(v) - abs(u) - abs(tanh((1/sqrt(2))*u)/(1/sqrt(2))) - abs(tanh((1/sqrt(2))*v)/(1/sqrt(2))) )*cos(v)
f_z = sin(u)*(abs(cos(4*u/4))^1 + abs(sin(4*u/4))^1)^(-1/1)
P = parametric_plot3d([f_x, f_y, f_z], (u, 0, pi), (v, -pi, pi),opacity=opacity)
elif example == 'Heart':
f_x = cos(u)*(4*sqrt(1-v^2)*sin(abs(u))^abs(u))
f_y = sin(u) *(4*sqrt(1-v^2)*sin(abs(u))^abs(u))
f_z = v
P = parametric_plot3d([f_x, f_y, f_z], (u, -pi, pi), (v, -1, 1), frame=False, color="red",opacity=opacity)
elif example == 'Green bowtie':
f_x = sin(u) / (sqrt(2) + sin(v))
f_y = sin(u) / (sqrt(2) + cos(v))
f_z = cos(u) / (1 + sqrt(2))
P = parametric_plot3d([f_x, f_y, f_z], (u, -pi, pi), (v, -pi, pi), frame=False, color="green",opacity=opacity)
elif example == "Boy's Surface":
url = "http://en.wikipedia.org/wiki/Boy's_surface"
fx = 2/3* (cos(u)* cos(2*v) + sqrt(2)* sin(u)* cos(v))* cos(u) / (sqrt(2) - sin(2*u)* sin(3*v))
fy = 2/3* (cos(u)* sin(2*v) - sqrt(2)* sin(u)* sin(v))* cos(u) / (sqrt(2) - sin(2*u)* sin(3*v))
fz = sqrt(2)* cos(u)* cos(u) / (sqrt(2) - sin(2*u)* sin(3*v))
P = parametric_plot3d([fx, fy, fz], (u, -2*pi, 2*pi), (v, 0, pi), plot_points = [90,90], frame=False, color="orange",opacity=opacity)
elif example == "Maeder's Owl":
fx = v *cos(u) - 0.5* v^2 * cos(2* u)
fy = -v *sin(u) - 0.5* v^2 * sin(2* u)
fz = 4 *v^1.5 * cos(3 *u / 2) / 3
P = parametric_plot3d([fx, fy, fz], (u, -2*pi, 2*pi), (v, 0, 1),plot_points = [90,90], frame=False, color="purple",opacity=opacity)
elif example =='Cross cap':
url = 'http://en.wikipedia.org/wiki/Cross-cap'
fx = (1+cos(v))*cos(u)
fy = (1+cos(v))*sin(u)
fz = -tanh((2/3)*(u-pi))*sin(v)
P = parametric_plot3d([fx, fy, fz], (u, 0, 2*pi), (v, 0, 2*pi), frame=False, color="red",opacity=opacity)
else:
print "Bug selecting plot?"
return
html('<h2>%s</h2>'%example)
if url:
html('<h3><a target="_new" href="%s">%s</a></h3>'%(url,url))
show(P, viewer='tachyon' if tachyon else 'jmol', frame=frame)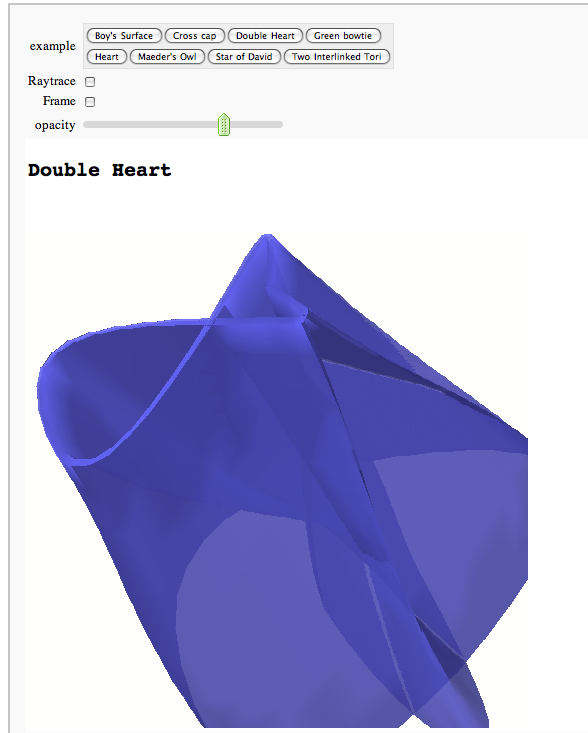
Interactive rotatable raytracing with Tachyon3d
C = cube(color=['red', 'green', 'blue'], aspect_ratio=[1,1,1],
viewer='tachyon') + sphere((1,0,0),0.2)
@interact
def example(theta=(0,2*pi), phi=(0,2*pi), zoom=(1,(1,4))):
show(C.rotate((0,0,1), theta).rotate((0,1,0),phi), zoom=zoom)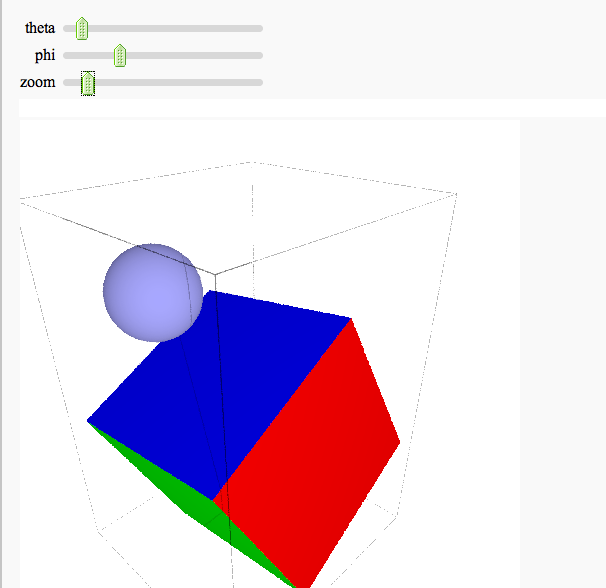
Interactive 3d plotting
var('x,y')
@interact
def example(clr=Color('orange'), f=4*x*exp(-x^2-y^2), xrange='(-2, 2)', yrange='(-2,2)',
zrot=(0,pi), xrot=(0,pi), zoom=(1,(1/2,3)), square_aspect=('Square Frame', False),
tachyon=('Ray Tracer', True)):
xmin, xmax = sage_eval(xrange); ymin, ymax = sage_eval(yrange)
P = plot3d(f, (x, xmin, xmax), (y, ymin, ymax), color=clr)
html('<h1>Plot of $f(x,y) = %s$</h1>'%latex(f))
aspect_ratio = [1,1,1] if square_aspect else [1,1,1/2]
show(P.rotate((0,0,1), -zrot).rotate((1,0,0),xrot),
viewer='tachyon' if tachyon else 'jmol',
figsize=6, zoom=zoom, frame=False,
frame_aspect_ratio=aspect_ratio)
Somewhat Silly Egg Painter
by Marshall Hampton (refereed by William Stein)
var('s,t')
g(s) = ((0.57496*sqrt(121 - 16.0*s^2))/sqrt(10.+ s))
def P(color, rng):
return parametric_plot3d((cos(t)*g(s), sin(t)*g(s), s), (s,rng[0],rng[1]), (t,0,2*pi), plot_points = [150,150], rgbcolor=color, frame = False, opacity = 1)
colorlist = ['red','blue','red','blue']@interact
def _(band_number = selector(range(1,5)), current_color = Color('red')):
html('<h1 align=center>Egg Painter</h1>')
colorlist[band_number-1] = current_color
egg = sum([P(colorlist[i],[-2.75+5.5*(i/4),-2.75+5.5*(i+1)/4]) for i in range(4)])
show(egg)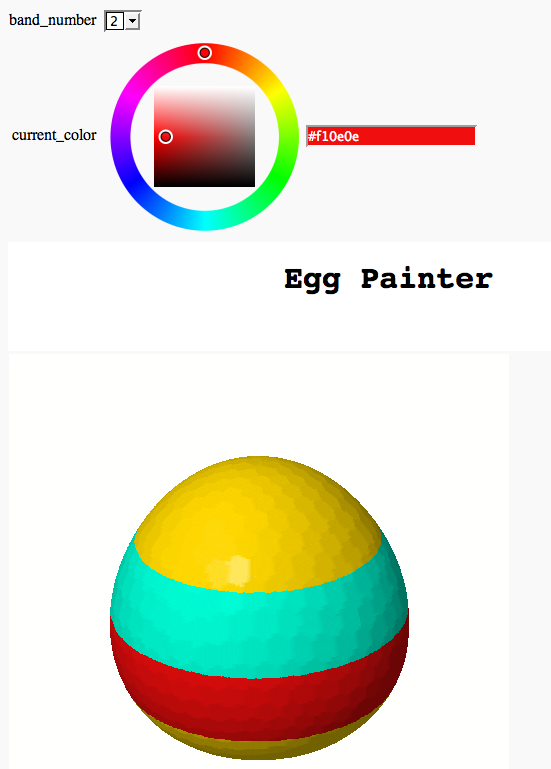
Plot Coloring
by Timothy Clemans
@interact
def color_experimenter(expression=input_box('', 'Expression', str), color=Color('red')):
if expression:
try:
plot(SR(expression), rgbcolor=color).show()
except TypeError:
print "There's a problem with your expression."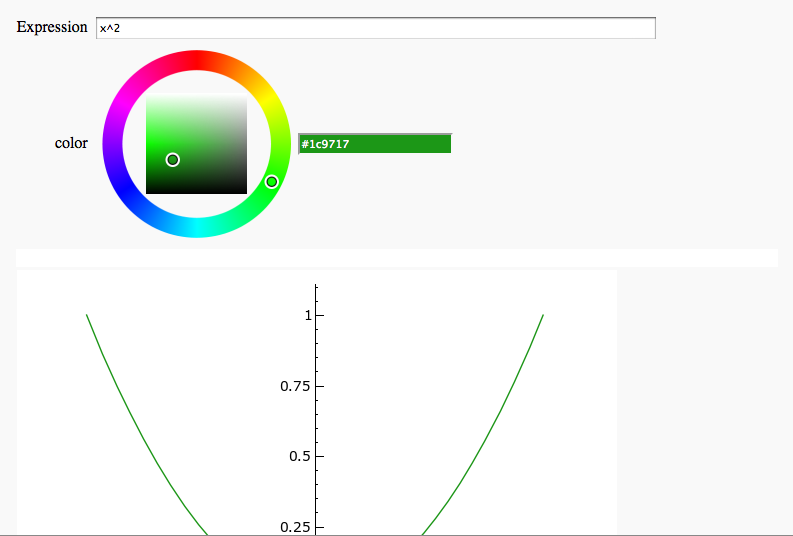
Interactive 2D Plotting
by Timothy Clemans
def error_msg(msg):
print '<html><p style="font-family:Arial, sans-serif;color:#000"><span style="color:red;font-weight:bold">Error</span>: %s</p></html>' % msg
@interact
def interactive_2d_plotter(expression=input_box('sin(x)', 'Expression', str), x_range=range_slider(-10,10,1,(0,10), label='X Range'), square=checkbox(True, 'Square'), axes=checkbox(False, 'Show Axes')):
if expression:
try:
expression = SR(expression) # turn string into a Sage expression
except TypeError:
print error_msg('This is not an expression.')
return
try:
xmin, xmax = x_range
if square or not axes:
print "var('%s')\nplot(%s).show(%s%s%s)" % (expression.variables()[0], repr(expression), 'aspect_ratio=1' if square else '', ', ' if square and not axes else '', 'axes=False' if not axes else '')
if square:
plot(expression, xmin, xmax).show(aspect_ratio=1, axes=axes)
else:
plot(expression, xmin, xmax).show(axes=axes)
else:
print "var('%s')\nplot(%s)" % (expression.variables()[0], repr(expression))
plot(expression, xmin, xmax).show(axes=axes)
except ValueError:
print error_msg('This expression has more than one variable.')
return
except TypeError:
print error_msg("This expression contains an unknown function.")
return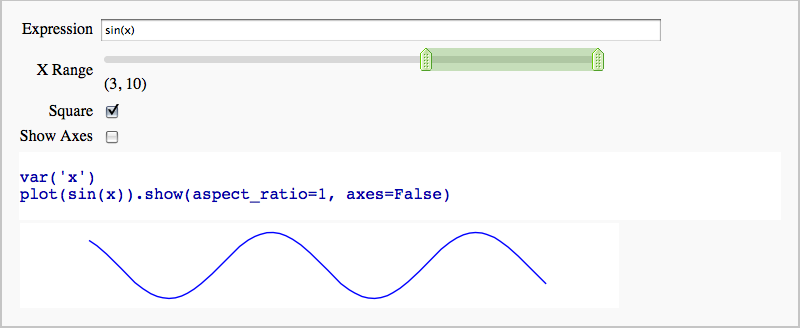
Interact with matplotlib
# Simple example demonstrating how to interact with matplotlib directly.
# Comment plt.clf() to get the plots overlay in each update.
# Gokhan Sever & Harald Schilly (2010-01-24)
from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
@interact
def plot_norm(loc=(0,(0,10)), scale=(1,(1,10))):
rv = stats.norm(loc, scale)
x = np.linspace(-10,10,1000)
plt.plot(x,rv.pdf(x))
plt.grid(True)
plt.savefig('plt.png')
plt.clf()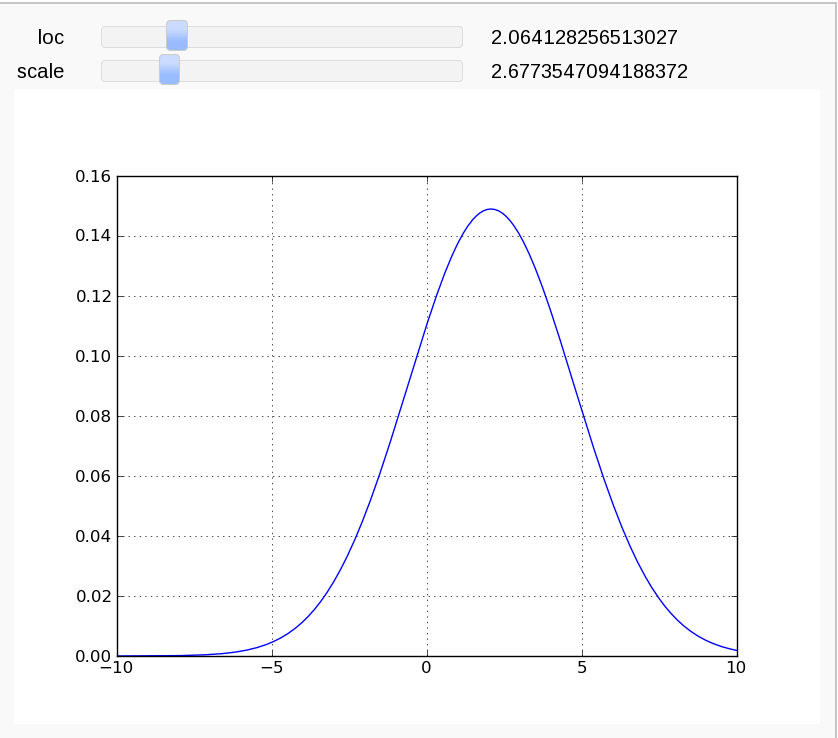
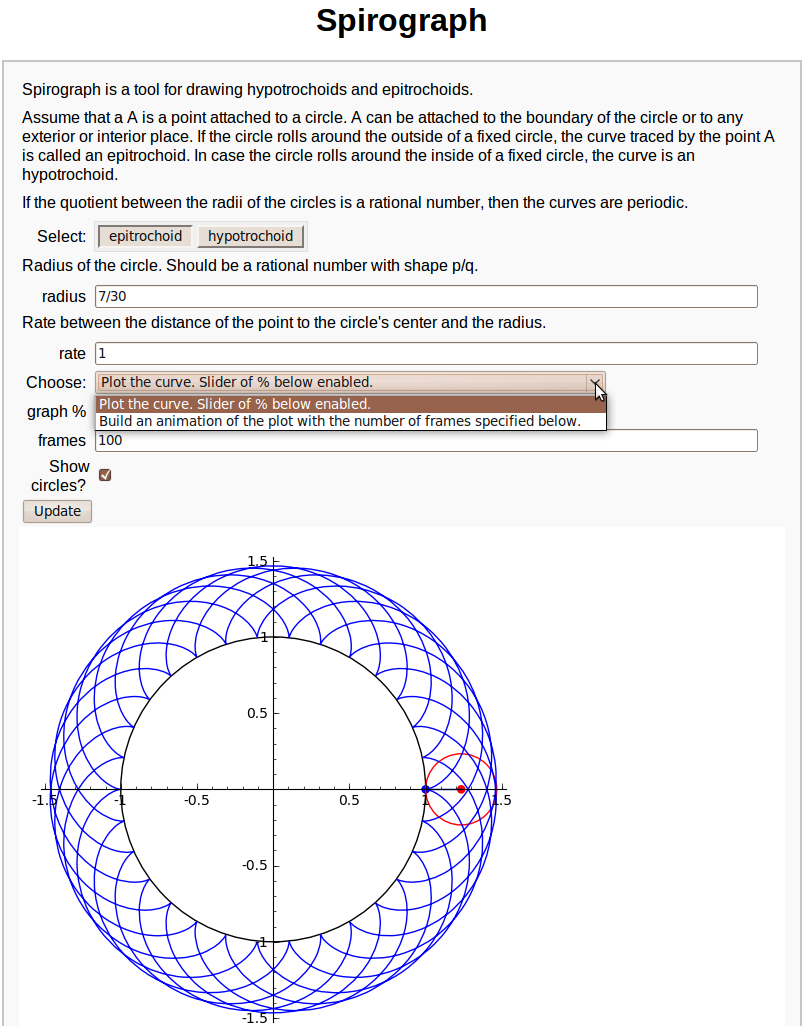
Spirograph
#---------------------------# # Javier Pérez Lázaro # # Logroño (Spain) # # [email protected] # #---------------------------# #introduction html('<h1><center>Spirograph</center></h1>') text1='Spirograph is a tool for drawing hypotrochoids and epitrochoids.' text2='Assume that a A is a point attached to a circle. A can be attached to the boundary of the circle or to any exterior or interior place. If the circle rolls around the outside of a fixed circle, the curve traced by the point A is called an epitrochoid. In case the circle rolls around the inside of a fixed circle, the curve is an hypotrochoid.' text3='If the quotient between the radii of the circles is a rational number, then the curves are periodic.' #the code @interact def fun( tex1=text_control(text1), tex2=text_control(text2), tex3=text_control(text3), h=('Select:',list(['epitrochoid','hypotrochoid'])), tex4=text_control('Radius of the circle. Should be a rational number with shape p/q.'), b=input_box(default=7/30,label='radius'), tex5=text_control("Rate between the distance of the point to the circle's center and the radius."), rate=input_box(default=1), u=selector(['Plot the curve. Slider of % below enabled.', 'Build an animation of the plot with the number of frames specified below.'],label='Choose:'), per=slider(0,100,1,default=100,label='graph %'), frames=100, cir_bool=checkbox(True, "Show circles?"), auto_update=false): draw=True if h=='hypotrochoid' and (b>=1 or b<=0): print "In a hypotrochoid, radius must be between 0 and 1." draw=False if h=='epitrochoid' and b<=0: print "In a epitrochoid, radius must be positive" draw=False if draw==True: if h=='hypotrochoid': b=-b var('t') cx=(1+b)*cos(t*b/(1+b)) cy=(1+b)*sin(t*b/(1+b)) px=cx-b*rate*cos(t) py=cy-b*rate*sin(t) axeM=1+max([0,b+abs(b)*rate]) if u=='Plot the curve. Slider of % below enabled.': tMax=pi*denominator(b/(b+1))*per/50 L=parametric_plot((px,py),(t,0,max([0.001,tMax])),plot_points=10*rate*tMax) if cir_bool: p=point((px(t=tMax),py(t=tMax)),pointsize=30,color='blue') c=point((cx(t=tMax),cy(t=tMax)),pointsize=30,color='red') cir=circle((cx(t=tMax),cy(t=tMax)),b,color='red') lin=line([(cx(t=tMax),cy(t=tMax)),(px(t=tMax),py(t=tMax))]) L+=circle((0,0),1)+cir+lin+p+c show(L,aspect_ratio=1,xmin=-axeM,xmax=axeM,ymin=-axeM,ymax=axeM) if u=='Build an animation of the plot with the number of frames specified below.': tMax=2*pi*denominator(b/(b+1)) step=tMax/(frames-1) curva=Graphics() v=[] for a in srange(step,tMax,step): curva+=parametric_plot((px,py),(t,a-step,a)) L=curva if cir_bool: cx_a=cx(t=a) cy_a=cy(t=a) px_a=cx_a-b*rate*cos(a) py_a=cy_a-b*rate*sin(a) p=point((px_a,py_a),pointsize=30,color='blue') c=point((cx_a,cy_a),pointsize=30,color='red') cir=circle((cx_a,cy_a),b,color='red') lin=line([(cx_a,cy_a),(px_a,py_a)]) L+=circle((0,0),1)+cir+lin+c+p v.append(L) animate(v,xmin=-axeM,xmax=axeM,ymin=-axeM,ymax=axeM,aspect_ratio=1).show()