|
Size: 10371
Comment:
|
Size: 14286
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 9: | Line 9: |
| {{{ | {{{#!sagecell |
| Line 11: | Line 11: |
| from math import cos,sin | |
| Line 13: | Line 12: |
| from math import cos, sin | |
| Line 51: | Line 51: |
| {{{ | {{{#!sagecell |
| Line 107: | Line 107: |
| print "Bug selecting plot?" | print("Bug selecting plot?") |
| Line 111: | Line 111: |
| html('<h2>%s</h2>'%example) | pretty_print(html('<h2>%s</h2>'%example)) |
| Line 113: | Line 113: |
| html('<h3><a target="_new" href="%s">%s</a></h3>'%(url,url)) show(P, viewer='tachyon' if tachyon else 'jmol', frame=frame) |
pretty_print(html('<h3><a target="_new" href="%s">%s</a></h3>'%(url,url))) show(P, viewer='tachyon' if tachyon else 'threejs', frame=frame) |
| Line 121: | Line 121: |
| {{{ | {{{#!sagecell |
| Line 134: | Line 134: |
| {{{ | {{{#!sagecell |
| Line 145: | Line 145: |
| viewer='tachyon' if tachyon else 'jmol', | viewer='tachyon' if tachyon else 'threejs', |
| Line 157: | Line 157: |
| {{{ | {{{#!sagecell |
| Line 163: | Line 163: |
| @interact def _(band_number = selector(range(1,5)), current_color = Color('red')): |
@interact def _(band_number = selector(range(1,5)), current_color = Color('red'), auto_update=False): |
| Line 174: | Line 175: |
| {{{ @interact def color_experimenter(expression=input_box('', 'Expression', str), color=Color('red')): |
{{{#!sagecell @interact def color_experimenter(expression=input_box('x^2', 'Expression', str), color=Color('red')): |
| Line 181: | Line 182: |
| print "There's a problem with your expression." | print("There's a problem with your expression.") else: print("Be sure to enter a plottable expression") |
| Line 185: | Line 188: |
| == Interactive 2d Plotting == | == Interactive 2D Plotting == |
| Line 187: | Line 190: |
| {{{ | {{{#!sagecell |
| Line 189: | Line 192: |
| print '<html><p style="font-family:Arial, sans-serif;color:#000"><span style="color:red;font-weight:bold">Error</span>: %s</p></html>' % msg | pretty_print(html('<p style="font-family:Arial, sans-serif;color:#000"><span style="color:red;font-weight:bold">Error</span>: %s</p>' % msg)) |
| Line 197: | Line 200: |
| print error_msg('This is not an expression.') | print(error_msg('This is not an expression.')) |
| Line 202: | Line 205: |
| print "var('%s')\nplot(%s).show(%s%s%s)" % (expression.variables()[0], repr(expression), 'aspect_ratio=1' if square else '', ', ' if square and not axes else '', 'axes=False' if not axes else '') | print("var('%s')\nplot(%s).show(%s%s%s)" % (expression.variables()[0], repr(expression), 'aspect_ratio=1' if square else '', ', ' if square and not axes else '', 'axes=False' if not axes else '')) |
| Line 208: | Line 211: |
| print "var('%s')\nplot(%s)" % (expression.variables()[0], repr(expression)) | print("var('%s')\nplot(%s)" % (expression.variables()[0], repr(expression))) |
| Line 211: | Line 214: |
| print error_msg('This expression has more than one variable.') | print(error_msg('This expression has more than one variable.')) |
| Line 214: | Line 217: |
| print error_msg("This expression contains an unknown function.") | print(error_msg("This expression contains an unknown function.")) |
| Line 220: | Line 223: |
| {{{ | {{{#!sagecell |
| Line 239: | Line 242: |
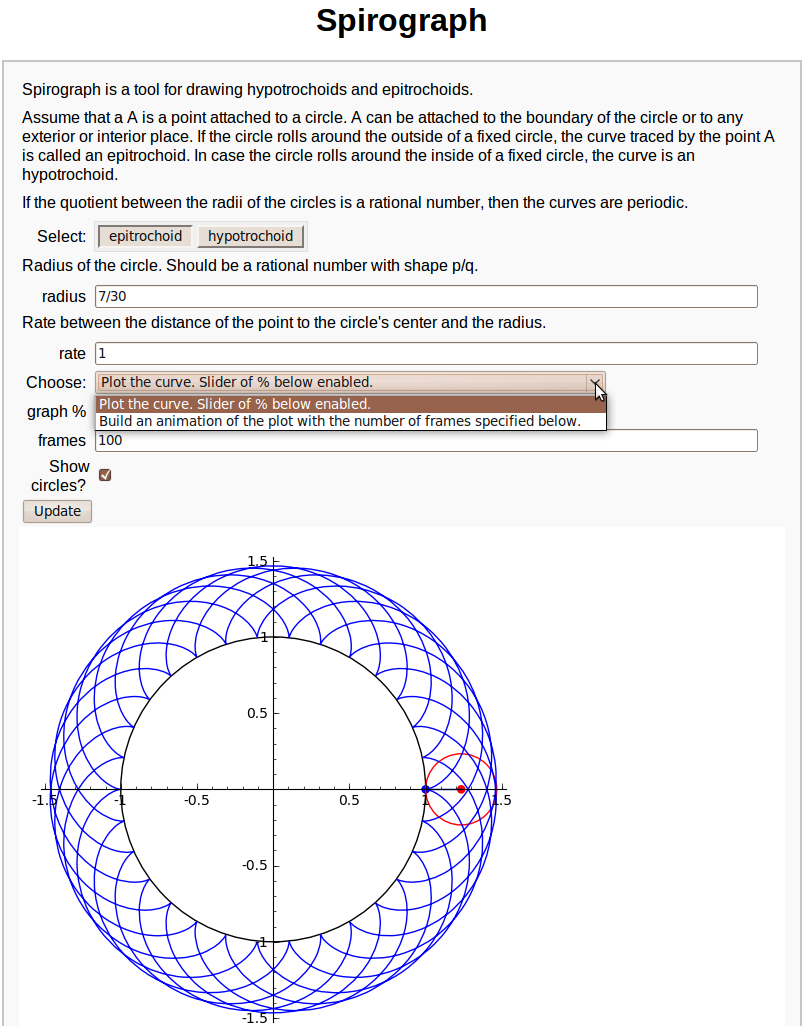
== Spirograph == {{{#!sagecell #---------------------------# # Javier Pérez Lázaro # # Logroño (Spain) # # [email protected] # #---------------------------# #introduction html('<h1><center>Spirograph</center></h1>') text1='Spirograph is a tool for drawing hypotrochoids and epitrochoids.' text2='Assume that a A is a point attached to a circle. A can be attached to the boundary of the circle or to any exterior or interior place. If the circle rolls around the outside of a fixed circle, the curve traced by the point A is called an epitrochoid. In case the circle rolls around the inside of a fixed circle, the curve is an hypotrochoid.' text3='If the quotient between the radii of the circles is a rational number, then the curves are periodic.' #the code @interact def fun( tex1=text_control(text1), tex2=text_control(text2), tex3=text_control(text3), h=('Select:',list(['epitrochoid','hypotrochoid'])), tex4=text_control('Radius of the circle. Should be a rational number with shape p/q.'), b=input_box(default=7/30,label='radius'), tex5=text_control("Rate between the distance of the point to the circle's center and the radius."), rate=input_box(default=1), u=selector(['Plot the curve. Slider of % below enabled.', 'Build an animation of the plot with the number of frames specified below.'],label='Choose:'), per=slider(0,100,1,default=100,label='graph %'), frames=100, cir_bool=checkbox(True, "Show circles?"), auto_update=false): draw=True if h == 'hypotrochoid' and (b >= 1 or b <= 0): print("In a hypotrochoid, radius must be between 0 and 1.") draw = False if h == 'epitrochoid' and b <= 0: print("In a epitrochoid, radius must be positive") draw=False if draw==True: if h=='hypotrochoid': b=-b var('t') cx=(1+b)*cos(t*b/(1+b)) cy=(1+b)*sin(t*b/(1+b)) px=cx-b*rate*cos(t) py=cy-b*rate*sin(t) axeM=1+max([0,b+abs(b)*rate]) if u=='Plot the curve. Slider of % below enabled.': tMax=pi*denominator(b/(b+1))*per/50 L=parametric_plot((px,py),(t,0,max([0.001,tMax])),plot_points=10*rate*tMax) if cir_bool: p=point((px(t=tMax),py(t=tMax)),pointsize=30,color='blue') c=point((cx(t=tMax),cy(t=tMax)),pointsize=30,color='red') cir=circle((cx(t=tMax),cy(t=tMax)),b,color='red') lin=line([(cx(t=tMax),cy(t=tMax)),(px(t=tMax),py(t=tMax))]) L+=circle((0,0),1)+cir+lin+p+c show(L,aspect_ratio=1,xmin=-axeM,xmax=axeM,ymin=-axeM,ymax=axeM) if u=='Build an animation of the plot with the number of frames specified below.': tMax=2*pi*denominator(b/(b+1)) step=tMax/(frames-1) curva=Graphics() v=[] for a in srange(step,tMax,step): curva+=parametric_plot((px,py),(t,a-step,a)) L=curva if cir_bool: cx_a=cx(t=a) cy_a=cy(t=a) px_a=cx_a-b*rate*cos(a) py_a=cy_a-b*rate*sin(a) p=point((px_a,py_a),pointsize=30,color='blue') c=point((cx_a,cy_a),pointsize=30,color='red') cir=circle((cx_a,cy_a),b,color='red') lin=line([(cx_a,cy_a),(px_a,py_a)]) L+=circle((0,0),1)+cir+lin+c+p v.append(L) animate(v,xmin=-axeM,xmax=axeM,ymin=-axeM,ymax=axeM,aspect_ratio=1).show() }}} {{attachment:interactive_animate_spirograph.png}} |
Sage Interactions - Graphics
goto interact main page
Contents
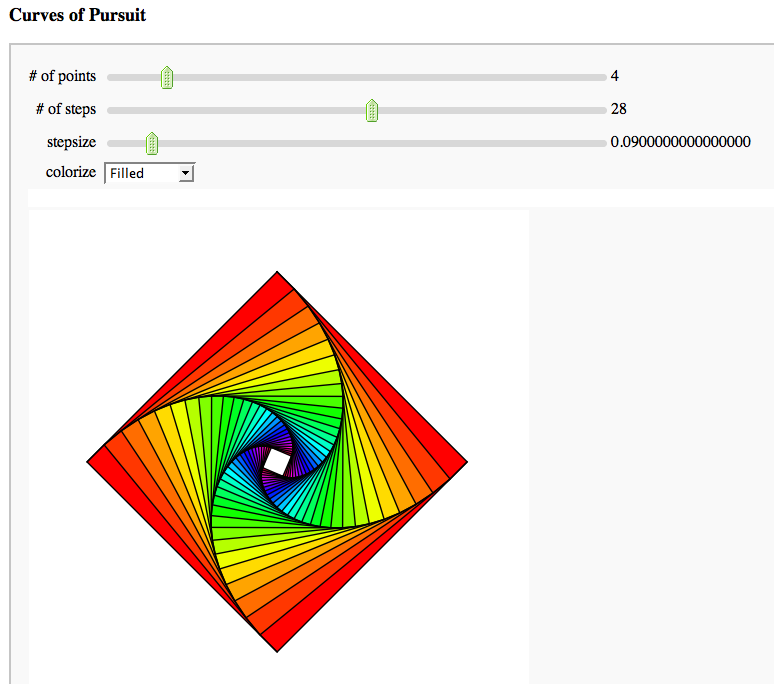
Curves of Pursuit
by Marshall Hampton.
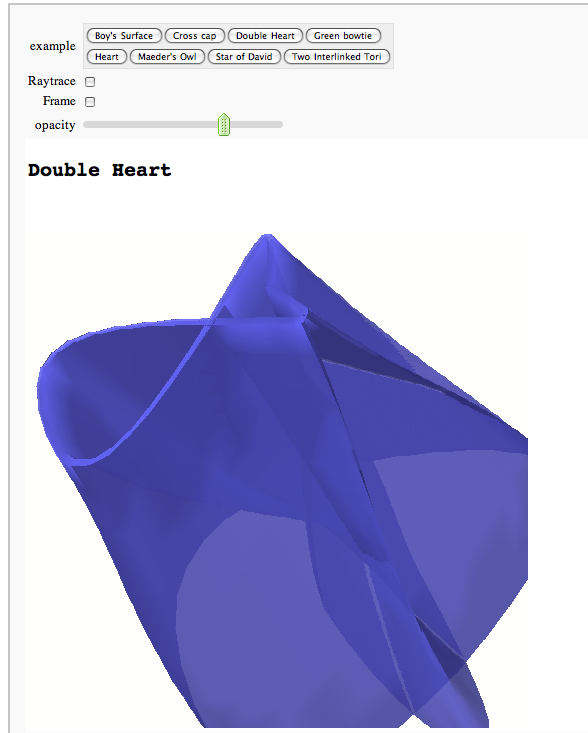
Catalog of 3D Parametric Plots
Interactive rotatable raytracing with Tachyon3d
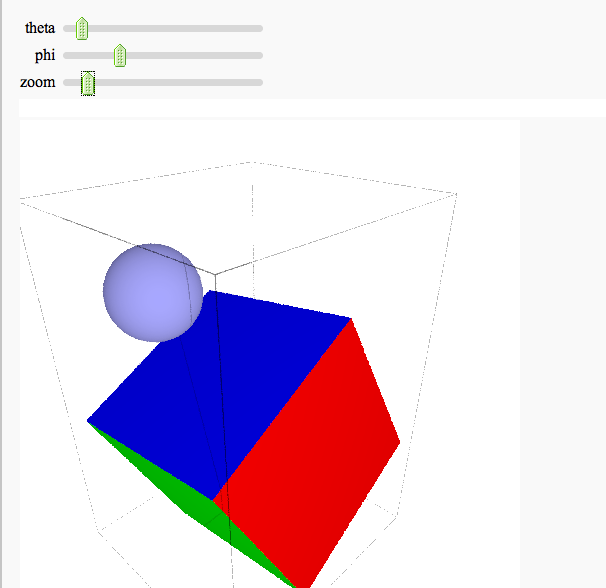
Interactive 3d plotting

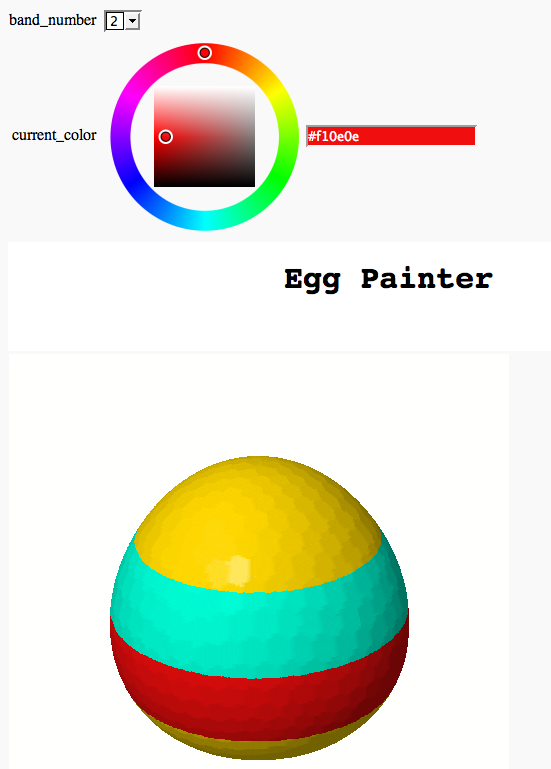
Somewhat Silly Egg Painter
by Marshall Hampton (refereed by William Stein)
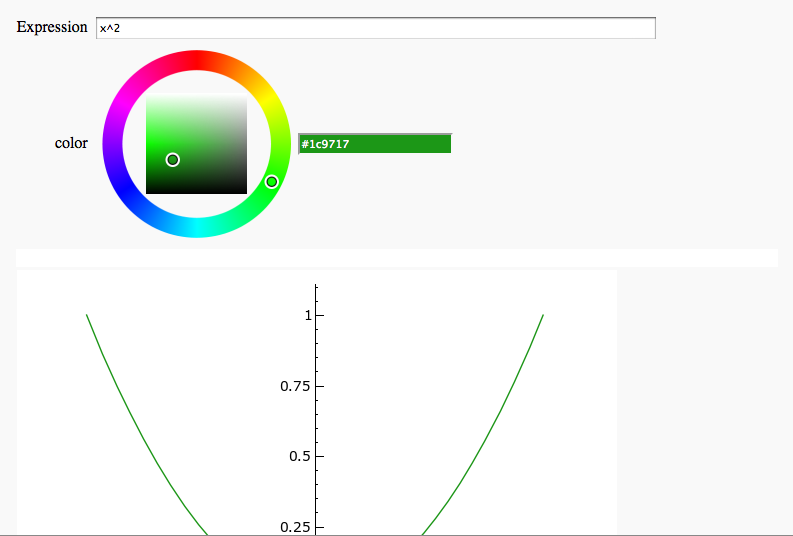
Plot Coloring
by Timothy Clemans
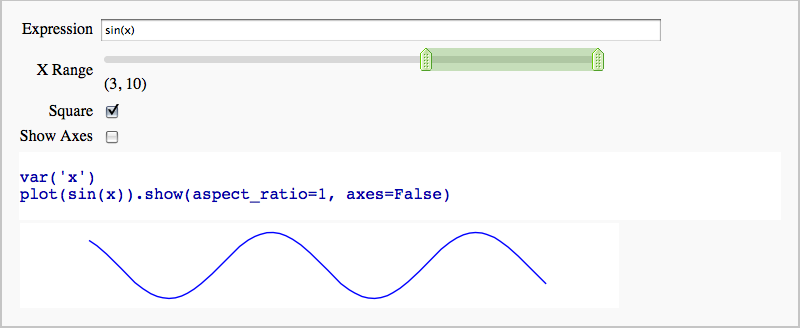
Interactive 2D Plotting
by Timothy Clemans
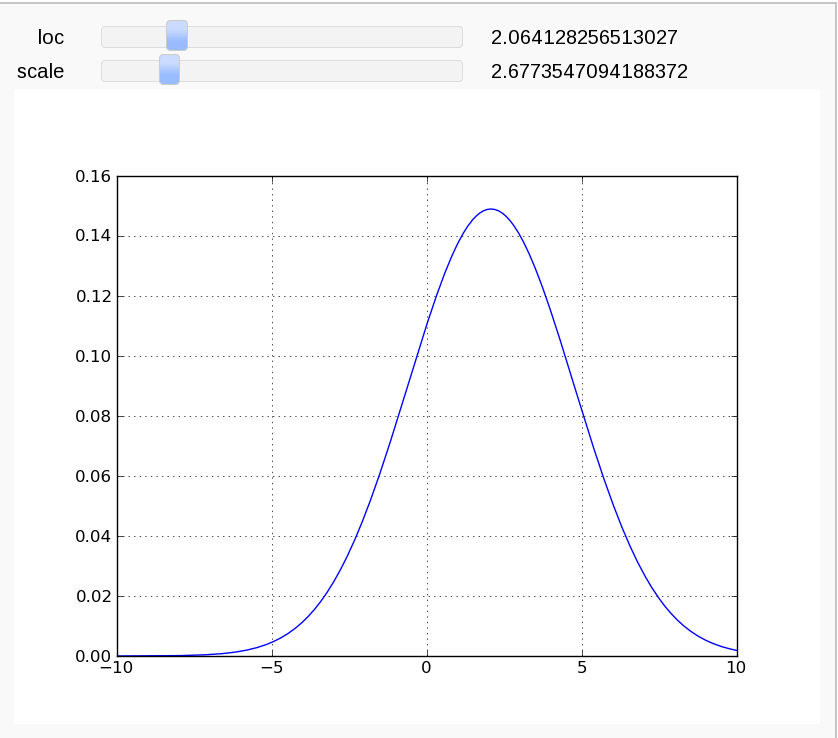
Interact with matplotlib
Spirograph