|
Size: 2287
Comment:
|
Size: 3213
Comment: converted to 1.6 markup
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| goto [:interact:interact main page] | goto [[interact|interact main page]] |
| Line 4: | Line 4: |
| [[TableOfContents]] | <<TableOfContents>> |
| Line 9: | Line 9: |
| grs = ['BalancedTree', 'BullGraph', 'ChvatalGraph', 'CirculantGraph', 'CircularLadderGraph', 'ClawGraph', 'CompleteBipartiteGraph', 'CompleteGraph', 'CubeGraph', 'CycleGraph', 'DegreeSequence', 'DegreeSequenceConfigurationModel', 'DegreeSequenceExpected', 'DegreeSequenceTree', 'DesarguesGraph', 'DiamondGraph', 'DodecahedralGraph', 'DorogovtsevGoltsevMendesGraph', 'EmptyGraph', 'FlowerSnark', 'FruchtGraph', 'Grid2dGraph', 'GridGraph', 'HeawoodGraph', 'HexahedralGraph', 'HoffmanSingletonGraph', 'HouseGraph', 'HouseXGraph', 'IcosahedralGraph', 'KrackhardtKiteGraph', 'LCFGraph', 'LadderGraph', 'LollipopGraph', 'MoebiusKantorGraph', 'OctahedralGraph', 'PappusGraph', 'PathGraph', 'PetersenGraph', 'RandomBarabasiAlbert', 'RandomGNM', 'RandomGNP', 'RandomHolmeKim', 'RandomLobster', 'RandomNewmanWattsStrogatz', 'RandomRegular', 'RandomTreePowerlaw', 'StarGraph', 'TetrahedralGraph', 'ThomsenGraph', 'WheelGraph'] | |
| Line 44: | Line 45: |
| attachment:graph_browse.png | {{attachment:graph_browse.png}} |
| Line 72: | Line 73: |
| attachment:auto_graph2.png | {{attachment:auto_graph2.png}} |
Sage Interactions - Graph Theory
goto interact main page
Graph Browser
by Marshall Hampton
grs = ['BalancedTree', 'BullGraph', 'ChvatalGraph', 'CirculantGraph', 'CircularLadderGraph', 'ClawGraph', 'CompleteBipartiteGraph', 'CompleteGraph', 'CubeGraph', 'CycleGraph', 'DegreeSequence', 'DegreeSequenceConfigurationModel', 'DegreeSequenceExpected', 'DegreeSequenceTree', 'DesarguesGraph', 'DiamondGraph', 'DodecahedralGraph', 'DorogovtsevGoltsevMendesGraph', 'EmptyGraph', 'FlowerSnark', 'FruchtGraph', 'Grid2dGraph', 'GridGraph', 'HeawoodGraph', 'HexahedralGraph', 'HoffmanSingletonGraph', 'HouseGraph', 'HouseXGraph', 'IcosahedralGraph', 'KrackhardtKiteGraph', 'LCFGraph', 'LadderGraph', 'LollipopGraph', 'MoebiusKantorGraph', 'OctahedralGraph', 'PappusGraph', 'PathGraph', 'PetersenGraph', 'RandomBarabasiAlbert', 'RandomGNM', 'RandomGNP', 'RandomHolmeKim', 'RandomLobster', 'RandomNewmanWattsStrogatz', 'RandomRegular', 'RandomTreePowerlaw', 'StarGraph', 'TetrahedralGraph', 'ThomsenGraph', 'WheelGraph']
examples = {}
for g in grs:
docs = eval('graphs.' + g + '.__doc__')
for docline in docs.split('\n'):
ex_loc = docline.find('graphs.' + g)
if ex_loc != -1:
end_paren_loc = docline[ex_loc:].find(')')
ex_str = docline[ex_loc:end_paren_loc+ex_loc+1]
ex_str = ex_str.replace('i+','2+')
ex_str = ex_str.replace('(i','(4')
break
try:
gt2 = eval(ex_str)
examples[g] = ex_str
except:
grs.remove(g)
@interact
def graph_browser(graph_name = selector(grs, label = "Graph type:"), newargs = input_box('',type=str,label='tuple of args'), output_type = selector(['2D','3D'], default='2D')):
base_g_str = 'graphs.' + graph_name
docs = eval(base_g_str + '.__doc__')
doc_ex_loc = docs.find('EXAMPLE')
if docs.find('PLOTTING') != -1:
doc_ex_loc = min(doc_ex_loc, docs.find('PLOTTING'))
print docs[0:doc_ex_loc].replace('\n ','\n')
if newargs != '':
try:
t_graph = eval(base_g_str + newargs)
except:
print "Invalid arguments, using default"
t_graph = eval(examples[graph_name])
else:
t_graph = eval(examples[graph_name])
if output_type == '2D': show(t_graph)
if output_type == '3D': t_graph.show3d()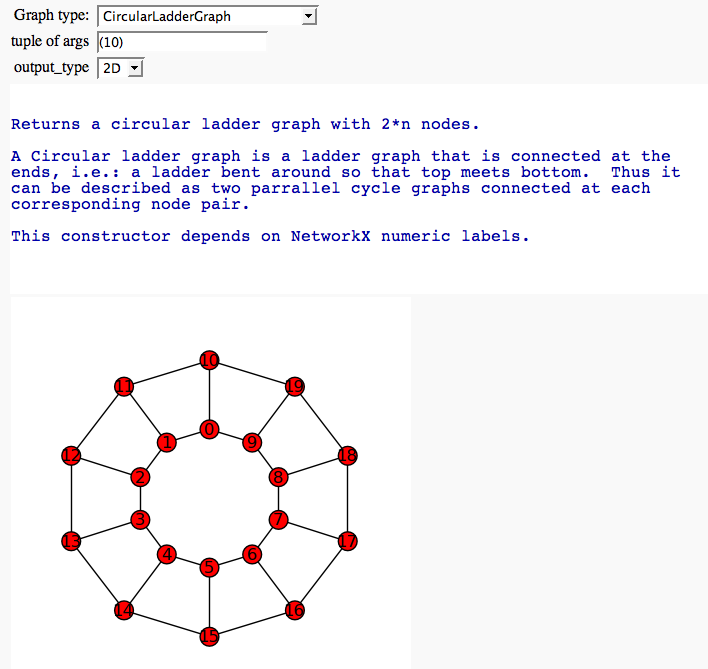
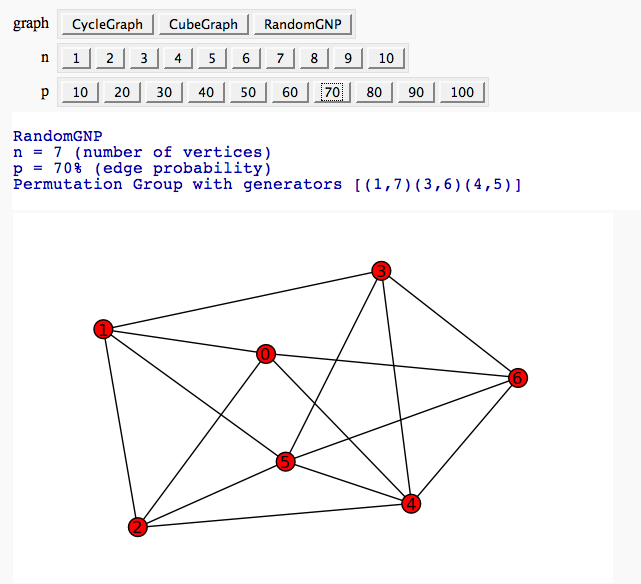
Automorphism Groups of some Graphs
by William Stein:
@interact
def _(graph=['CycleGraph', 'CubeGraph', 'RandomGNP'],
n=selector([1..10],nrows=1), p=selector([10,20,..,100],nrows=1)):
print graph
if graph == 'CycleGraph':
print "n = %s (number of vertices)"%n
G = graphs.CycleGraph(n)
elif graph == 'CubeGraph':
if n > 8:
print "n reduced to 8"
n = 8
print "n = %s (dimension)"%n
G = graphs.CubeGraph(n)
elif graph == 'RandomGNP':
print "n = %s (number of vertices)"%n
print "p = %s%% (edge probability)"%p
G = graphs.RandomGNP(n, p/100.0)
print G.automorphism_group()
show(plot(G))