|
Size: 8202
Comment:
|
Size: 8292
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 8: | Line 8: |
| {{{ | {{{#!sagecell |
| Line 45: | Line 45: |
| {{{ | {{{#!sagecell |
| Line 69: | Line 69: |
| {{{ | {{{#!sagecell |
| Line 93: | Line 93: |
| {{{ | {{{#!sagecell |
| Line 125: | Line 125: |
| {{{ | {{{#!sagecell |
| Line 154: | Line 154: |
| {{{ | {{{#!sagecell |
| Line 204: | Line 204: |
| {{{ | {{{#!sagecell |
| Line 241: | Line 241: |
| {{{ | {{{#!sagecell |
| Line 273: | Line 273: |
| {{{ | {{{#!sagecell |
Sage Interactions - Fractal
goto interact main page
Contents
-
Sage Interactions - Fractal
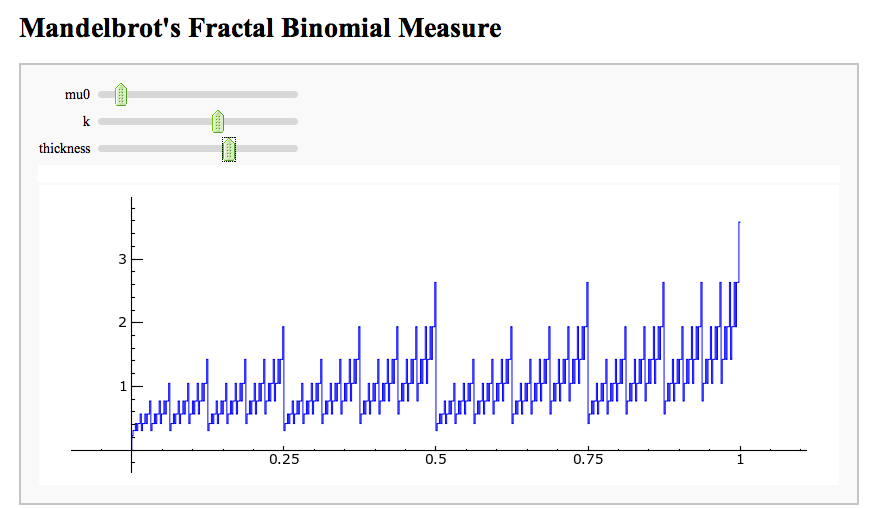
- Mandelbrot's Fractal Binomial Distribution
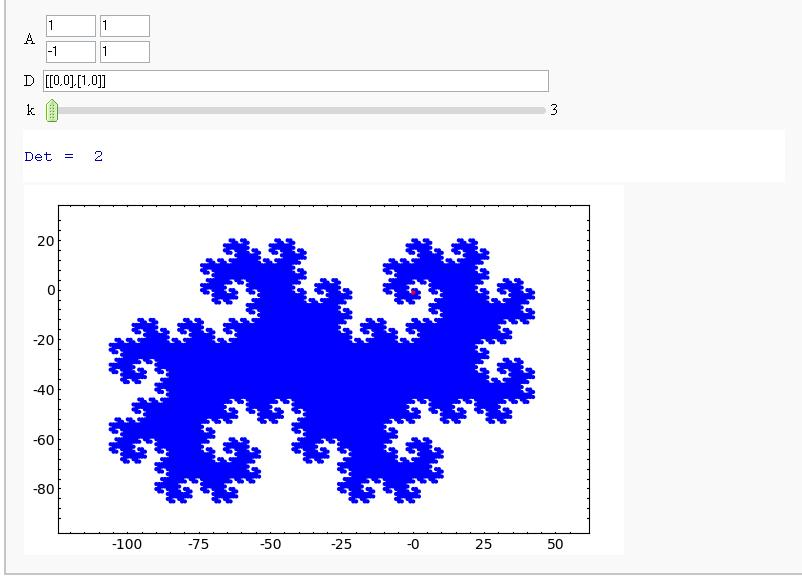
- Fractals Generated By Digit Sets and Dilation Matrices (Sage Days 9 - Avra Laarakker)
- Attempt at Generating all integer vectors with Digits D and Matrix A (How about vector([0,-1])?)
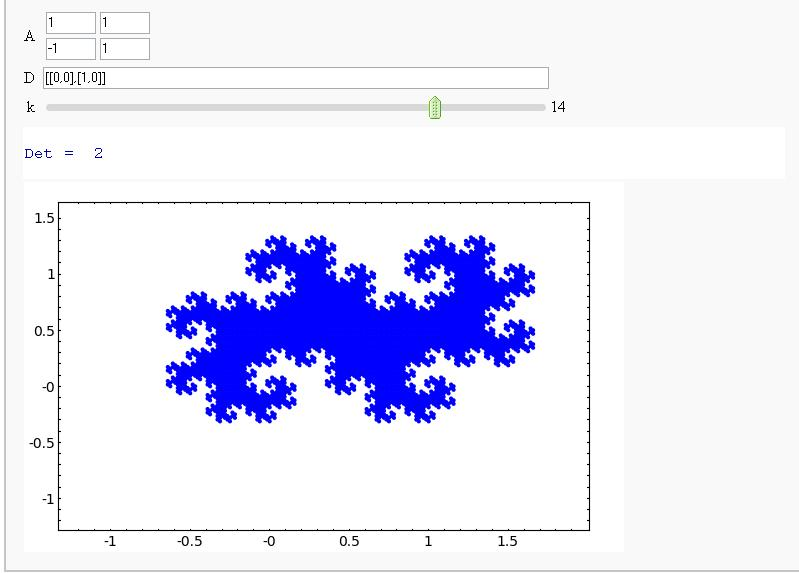
- Demonstrating that the Twin Dragon Matrix is likely to yield a Tiling of a Compact Interval of R^2 as k->infinity (It does!)
- Now in 3D
- Exploring Mandelbrot
- Mandelbrot & Julia Interact with variable exponent
- Sierpiński Triangle
Mandelbrot's Fractal Binomial Distribution
Fractals Generated By Digit Sets and Dilation Matrices (Sage Days 9 - Avra Laarakker)
Attempt at Generating all integer vectors with Digits D and Matrix A (How about vector([0,-1])?)
Demonstrating that the Twin Dragon Matrix is likely to yield a Tiling of a Compact Interval of R^2 as k->infinity (It does!)
Now in 3D
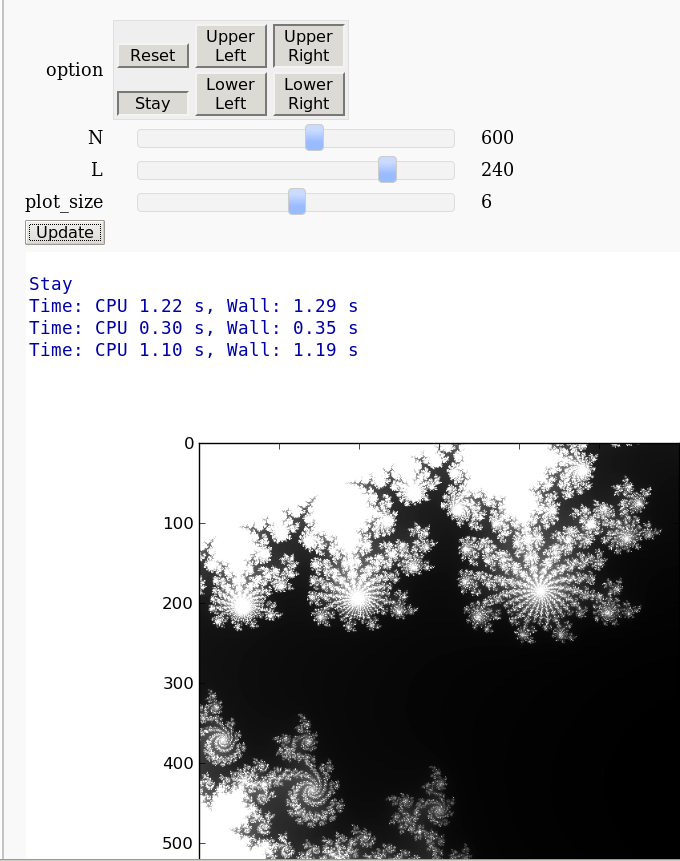
Exploring Mandelbrot
Pablo Angulo
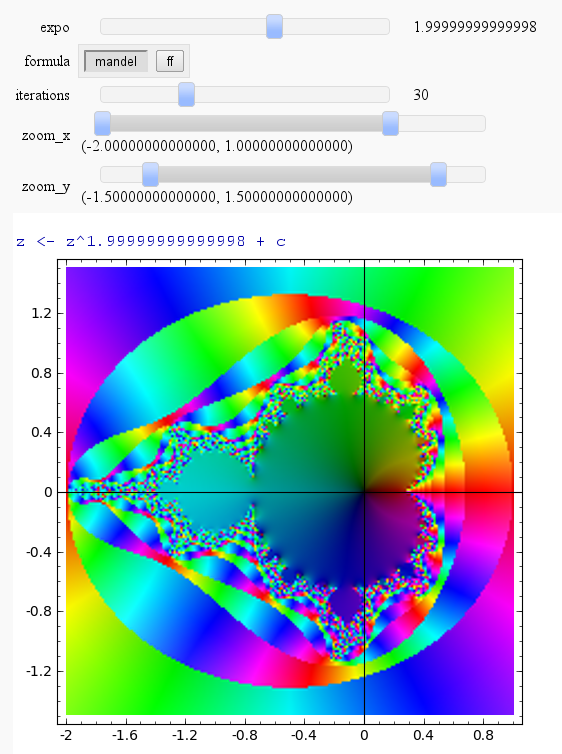
Mandelbrot & Julia Interact with variable exponent
published notebook: http://sagenb.org/pub/1299/
Mandelbrot
by Harald Schilly
Julia
by Harald Schilly
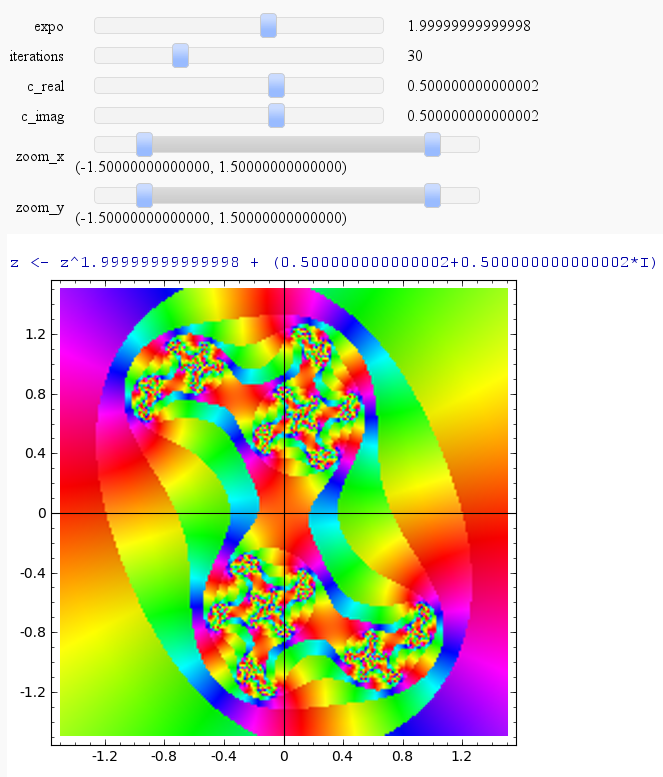
julia_plot(-7,30,0.5,0.5,(-1.5,1.5), (-1.5,1.5))
Sierpiński Triangle
by Eviatar Bach