Differences between revisions 18 and 27 (spanning 9 versions)
⇤ ← Revision 18 as of 2009-12-28 16:59:25 →
Size: 6070
Editor: schilly
Comment:
← Revision 27 as of 2012-04-18 18:02:48 → ⇥
Size: 8292
Editor: bvarberg
Comment:
Deletions are marked like this. Additions are marked like this.
Line 8: Line 8:
{{{ {{{#!sagecell
Line 45: Line 45:
{{{ {{{#!sagecell
Line 69: Line 69:
{{{ {{{#!sagecell
Line 91: Line 91:
== Now in 3d ==
    
{{{		 == Now in 3D ==
    
{{{#!sagecell
Line 125: Line 125:
{{{ {{{#!sagecell
Line 128: Line 128:
def mandelbrot_cython(float x0,float x1,float y0,float y1,int N=200, int L=50, float R=3): cimport numpy as np

def mandelbrot_cython(float x0,float x1,float y0,float y1,                     int N=200, int L=50, float R=3):
Line 131: Line 134:
    cdef int h, i, k
    m= np.zeros([N,N], dtype=np.int)
    for i in range(N):		     cdef double complex c, z, I
    cdef float deltax, deltay, R2 = R*R
    cdef int h, j, k
    cdef np.ndarray[np.uint16_t, ndim=2] m
    m = np.zeros((N,N), dtype=np.uint16)
    I = complex(0,1)
    deltax = (x1-x0)/N
    deltay = (y1-y0)/N
    for j in range(N):
Line 135: Line 144:
            c=complex(x0+i*(x1-x0)/N, y0+k*(y1-y0)/N)
            z=complex(0,0)		             c = (x0+j*deltax)+ I*(y0+k*deltay)
            z=0
Line 138: Line 147:
            while (h<L) and (abs(z)<R):             while (h<L and
                   z.real**2 + z.imag**2 < R2):
Line 141: Line 151:
            m[i,k]=h             m[j,k]=h
Line 144: Line 154:
{{{
@interact
def showme_mandelbrot(x0=-2, y0=-1.5, side=3.0,N=(100*i for i in range(1,11)), L=(20*i for i in range(1,11)) ):		 {{{#!sagecell
import pylab
x0_default = -2
y0_default = -1.5
side_default = 3.0
side = side_default
x0 = x0_default
y0 = y0_default
options = ['Reset','Upper Left', 'Upper Right', 'Stay', 'Lower Left', 'Lower Right']

@interact
def show_mandelbrot(option = selector(options, nrows = 2, width=8),
                    N = slider(100, 1000,100, 300),
                    L = slider(20, 300, 20, 60),
                    plot_size = slider(2,10,1,6),
                    auto_update = False):
    global x0, y0, side
    if option == 'Lower Right':
        x0 += side/2
        y0 += side/2
    elif option == 'Upper Right':
        y0 += side/2
    elif option == 'Lower Left':
        x0 += side/2
    if option=='Reset':
        side = side_default
        x0 = x0_default
        y0 = y0_default
    elif option != 'Stay':
        side = side/2
    
Line 148: Line 186:
    time show(matrix_plot(m)) # p = (matrix_plot(m) +
# line2d([(N/2,0),(N/2,N)], color='red', zorder=2) +
# line2d([(0,N/2),(N,N/2)], color='red', zorder=2))
# time show(p, figsize = (plot_size, plot_size))
    pylab.clf()
    pylab.imshow(m, cmap = pylab.cm.gray)
    time pylab.savefig('mandelbrot.png')
Line 160: Line 204:
{{{ {{{#!sagecell
Line 163: Line 207:
      formula = list(['mandel','ff']),\       formula = ['mandel','ff'],\
Line 197: Line 241:
{{{ {{{#!sagecell
Line 225: Line 269:

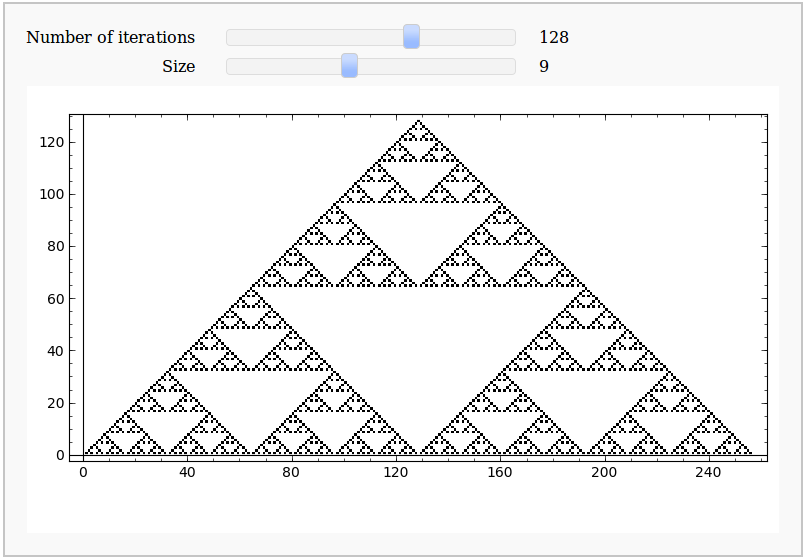
== Sierpiński Triangle ==
by Eviatar Bach

{{{#!sagecell
%python

from numpy import zeros

def sierpinski(N):
    '''Generates the Sierpiński Triangle fractal to N iterations using the Rule 90 elementary cellular automaton. N is in powers of 2 because these produce "whole" triangles.'''
    M=zeros( (N,2*N+1), dtype=int)
    M[0,N]=1
    rule=[0, 1, 0, 1, 1, 0, 1, 0]
    
    for j in range(1,N):
        for k in range(N-j,N+j+1):
            l = 4*M[j-1,k-1] + 2*M[j-1,k] + M[j-1,k+1]
            M[j,k]=rule[ l ]
    return M
    
@interact
def _(N=slider([2**a for a in range(0, 12)], label='Number of iterations',default=128), size = slider(1, 20, label= 'Size', step_size=1, default=9 )):
    M = sierpinski(N)
    plot_M = matrix_plot(M, cmap='binary')
    plot_M.show( figsize=[size,size])
}}}
{{attachment:sierpinski.png}}

Sage Interactions - Fractal

goto interact main page

Contents

  1. Sage Interactions - Fractal
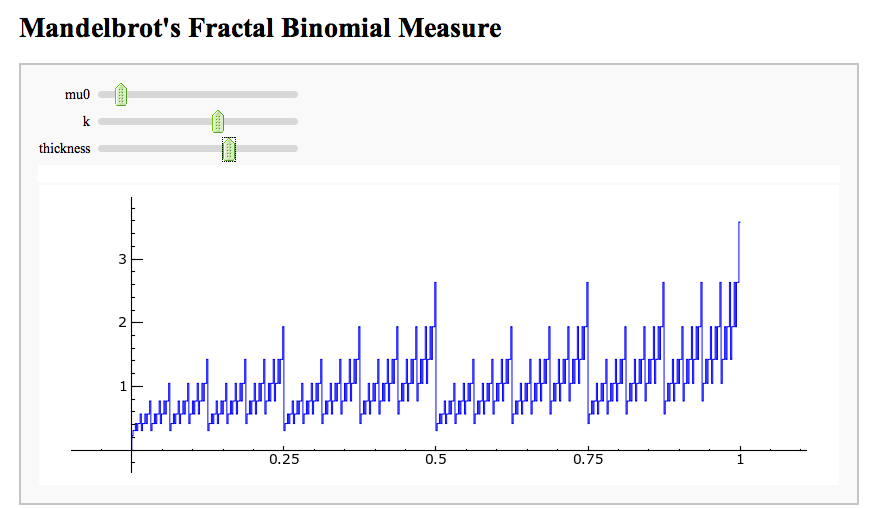
    1. Mandelbrot's Fractal Binomial Distribution
    2. Fractals Generated By Digit Sets and Dilation Matrices (Sage Days 9 - Avra Laarakker)
    3. Attempt at Generating all integer vectors with Digits D and Matrix A (How about vector([0,-1])?)
    4. Demonstrating that the Twin Dragon Matrix is likely to yield a Tiling of a Compact Interval of R^2 as k->infinity (It does!)
    5. Now in 3D
    6. Exploring Mandelbrot
    7. Mandelbrot & Julia Interact with variable exponent
      1. Mandelbrot
      2. Julia
    8. Sierpiński Triangle

Mandelbrot's Fractal Binomial Distribution

binomial.png

Fractals Generated By Digit Sets and Dilation Matrices (Sage Days 9 - Avra Laarakker)

Attempt at Generating all integer vectors with Digits D and Matrix A (How about vector([0,-1])?)

1.png

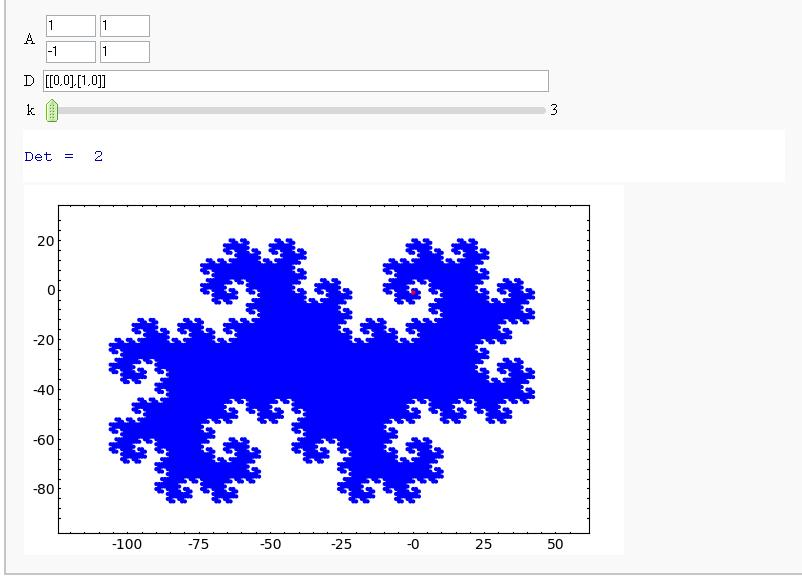
Demonstrating that the Twin Dragon Matrix is likely to yield a Tiling of a Compact Interval of R^2 as k->infinity (It does!)

2.png

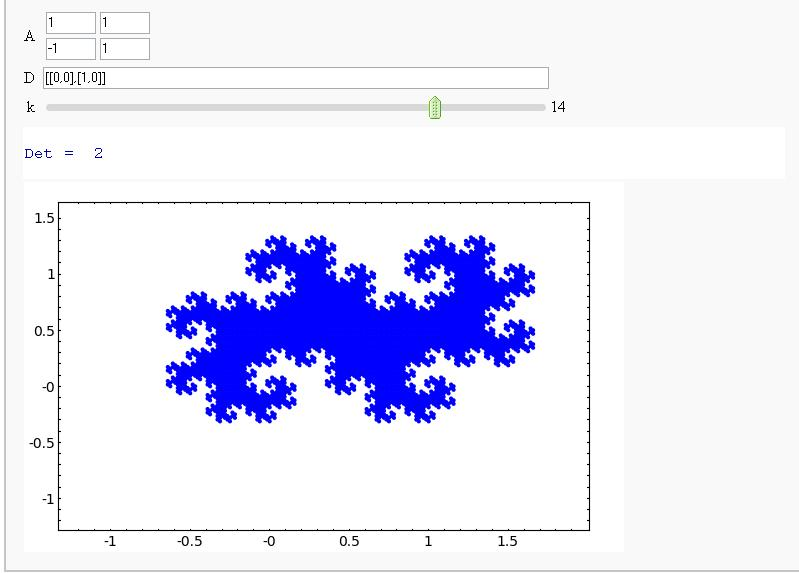
Now in 3D

3.png

4.png

CategoryCategory

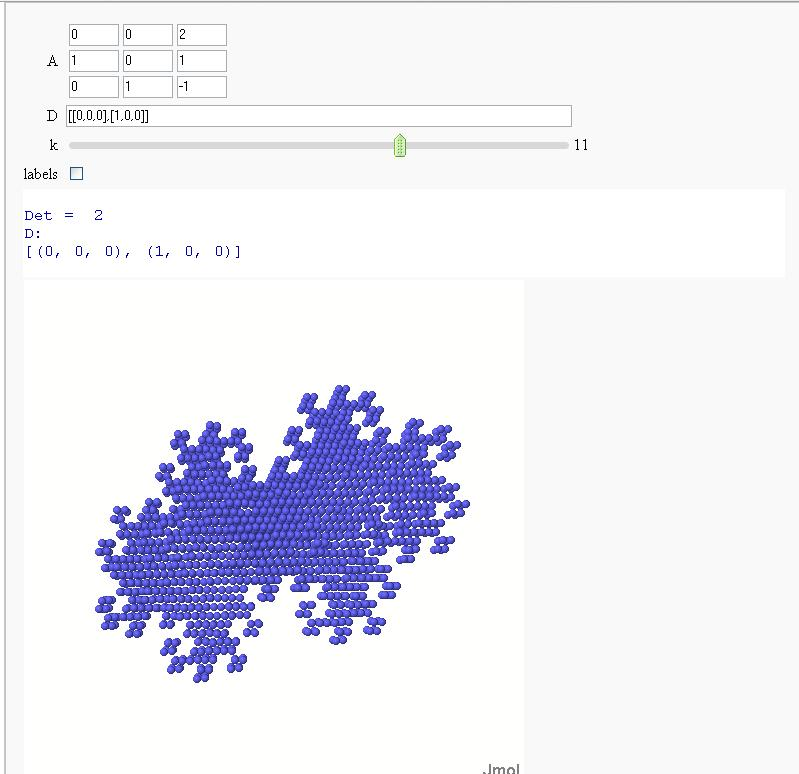
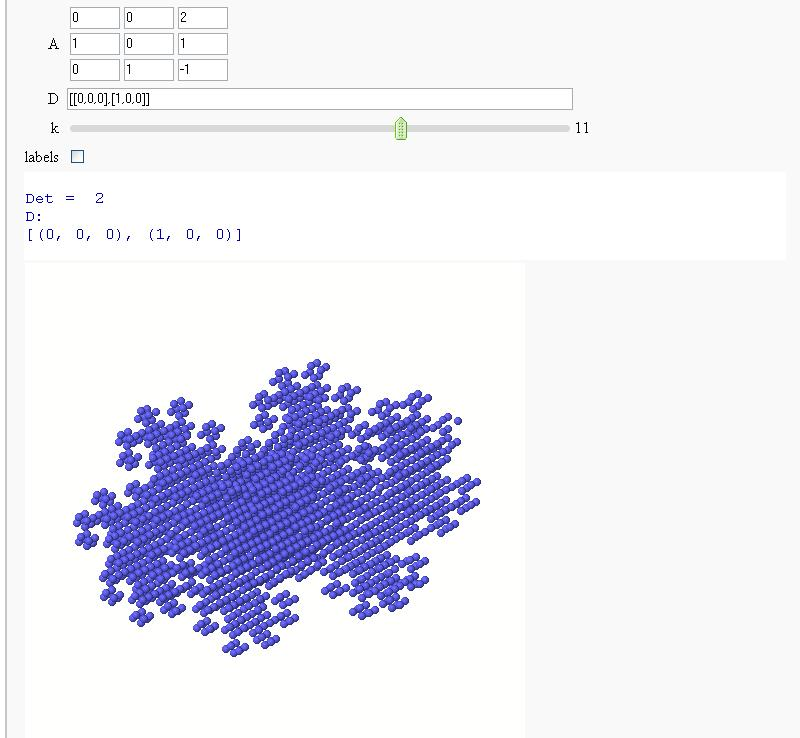
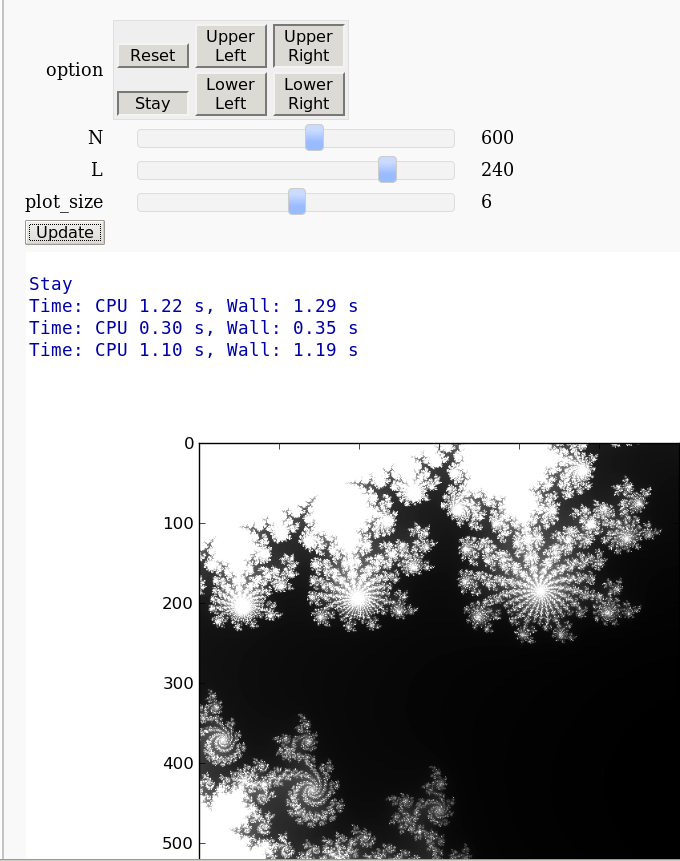
Exploring Mandelbrot

Pablo Angulo

mandelbrot_cython.png

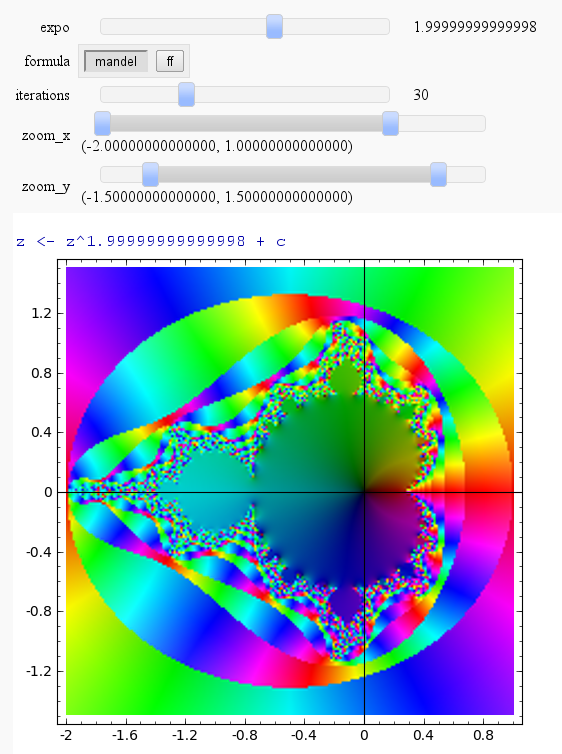
Mandelbrot & Julia Interact with variable exponent

published notebook: http://sagenb.org/pub/1299/

Mandelbrot

by Harald Schilly

mandel-interact-02.png

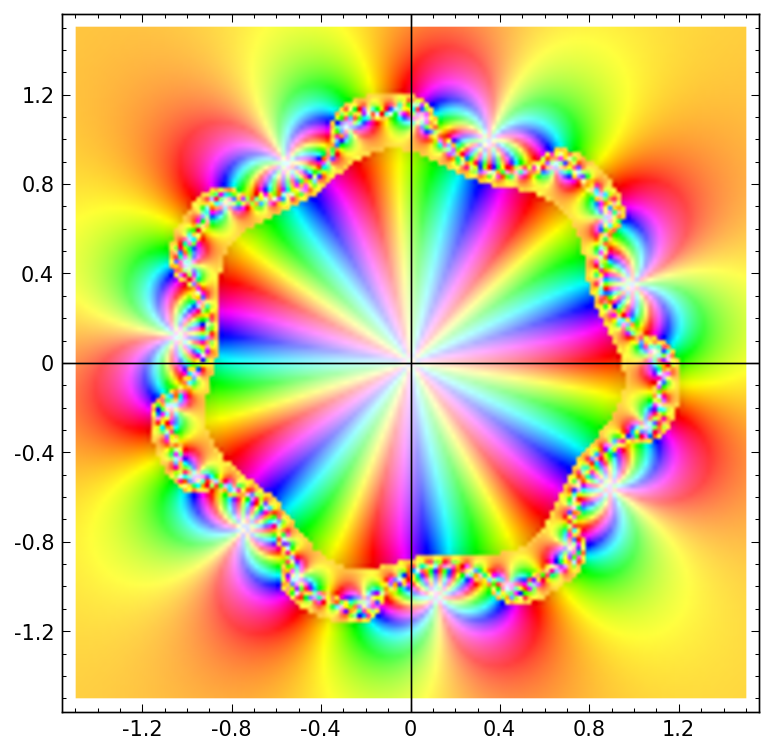
Julia

by Harald Schilly

julia-interact-01.png 

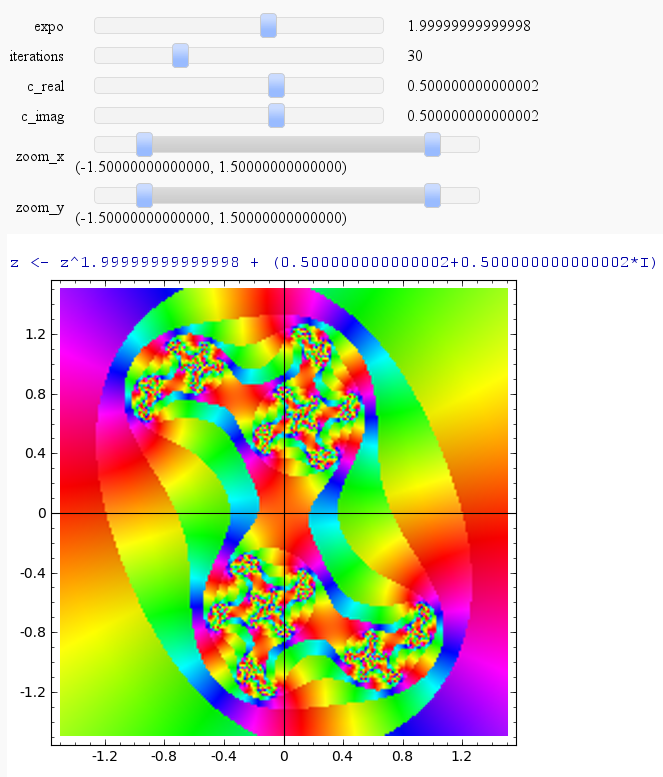
julia_plot(-7,30,0.5,0.5,(-1.5,1.5), (-1.5,1.5))

julia-fractal-exponent--7.png

Sierpiński Triangle

by Eviatar Bach

sierpinski.png

interact/fractal (last edited 2019-04-06 16:11:28 by chapoton)