|
Size: 62900
Comment: fix a NotImplementedError and a DeprecationWarning in Taylor Series
|
Size: 62928
Comment: set homogeneous label format in Illustration of the precise definition of a limit
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 549: | Line 549: |
| def delta_epsilon(f = input_box(default=(x^2-x)/(x-1)), a=input_box(default=1), L = input_box(default=1), delta=input_box(label="δ",default=0.1), epsilon=input_box(label="ε",default=0.1), xm=input_box(label="<i>x</i><sub>min</sub>",default=-1), xM=input_box(label="<i>x</i><sub>max</sub>",default=4)): | def delta_epsilon(f = input_box(default=(x^2-x)/(x-1), label=$f$), a=input_box(default=1, label=$a$), L = input_box(default=1, label=$L$), delta=input_box(label=r"$\delta$",default=0.1), epsilon=input_box(label=r"$\varepsilon$",default=0.1), xm=input_box(label=r"$x_{min}$",default=-1), xM=input_box(label=r"$x_{max}$",default=4)): |
Sage Interactions - Calculus
goto interact main page
Contents
-
Sage Interactions - Calculus
- Root Finding Using Bisection
- Newton's Method
- A contour map and 3d plot of two inverse distance functions
- A simple tangent line grapher
- Numerical integrals with the midpoint rule
- Numerical integrals with various rules
- Some polar parametric curves
- Function tool
- Newton-Raphson Root Finding
- Coordinate Transformations (FIXME in Jupyter)
- Taylor Series
- Illustration of the precise definition of a limit
- A graphical illustration of sin(x)/x -> 1 as x-> 0
- Quadric Surface Plotter
- The midpoint rule for numerically integrating a function of two variables
- Gaussian (Legendre) quadrature
- Vector Calculus, 2-D Motion
- Vector Calculus, 3-D Motion (FIXME)
- Multivariate Limits by Definition
- Directional Derivatives
- 3D graph with points and curves
- Approximating function in two variables by differential
- Taylor approximations in two variables
- Volumes over non-rectangular domains
- Lateral Surface Area (FIXME in Jupyter)
- Parametric surface example (FIXME in Jupyter)
- Line Integrals in 3D Vector Field
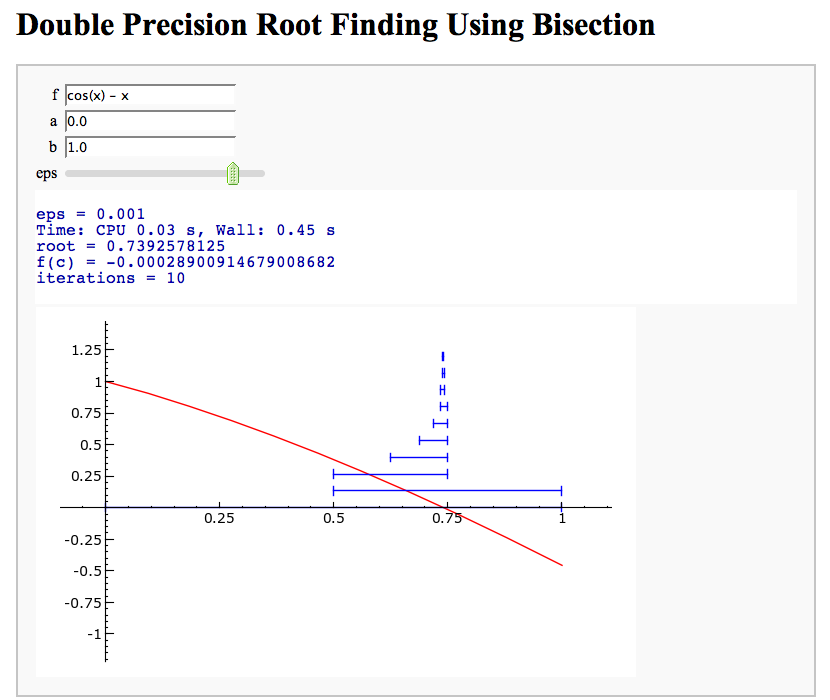
Root Finding Using Bisection
by William Stein
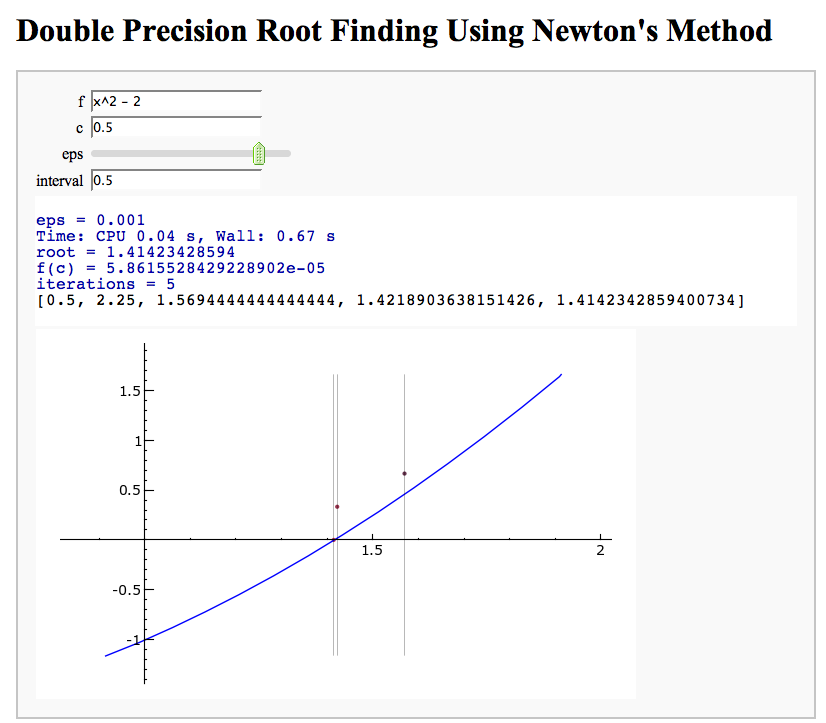
Newton's Method
Note that there is a more complicated Newton's method below.
by William Stein
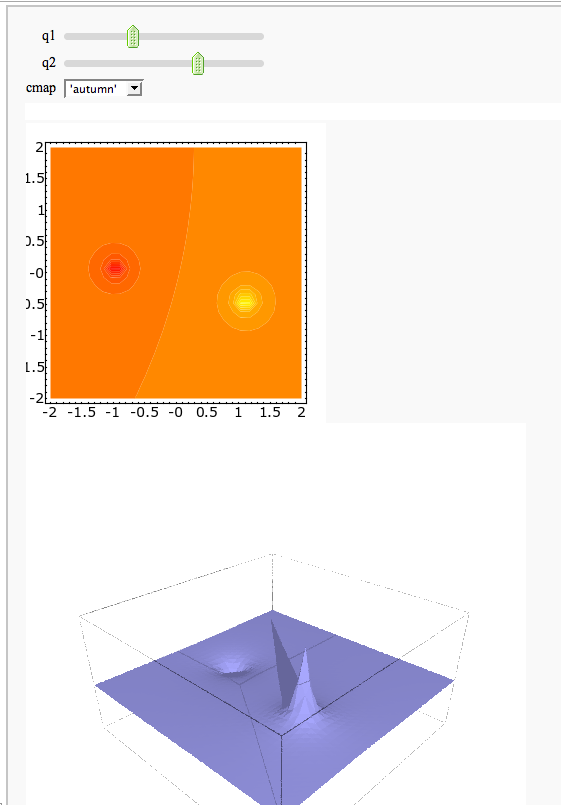
A contour map and 3d plot of two inverse distance functions
by William Stein
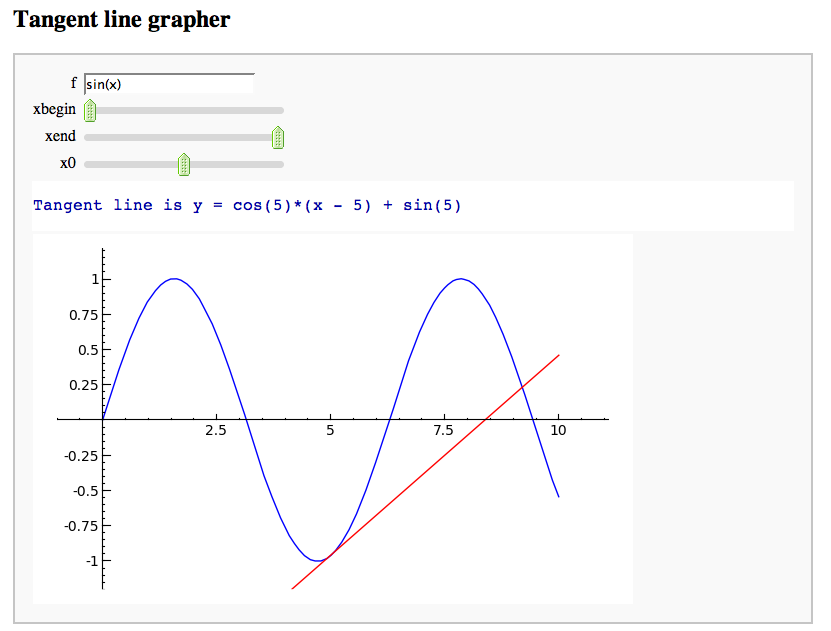
A simple tangent line grapher
by Marshall Hampton
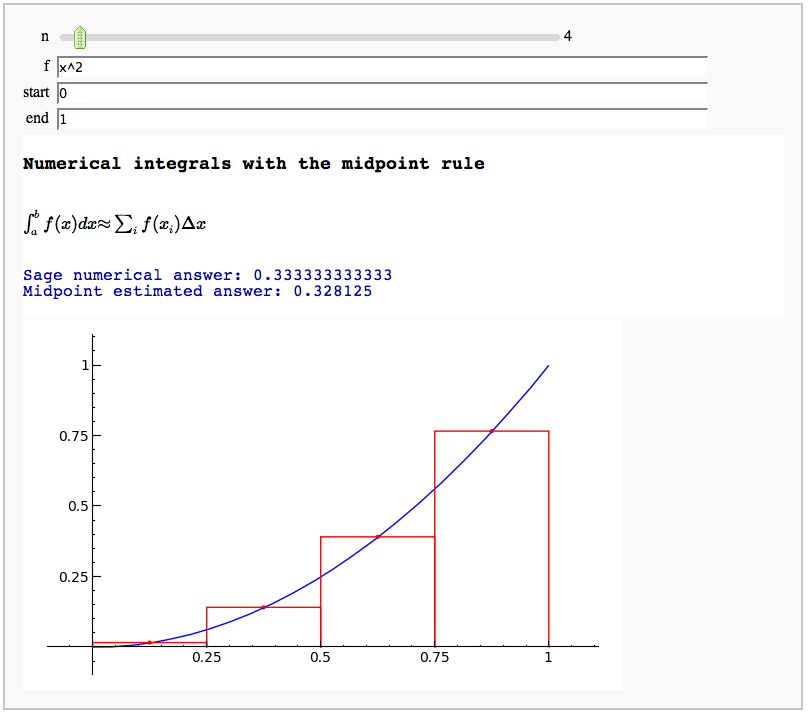
Numerical integrals with the midpoint rule
by Marshall Hampton
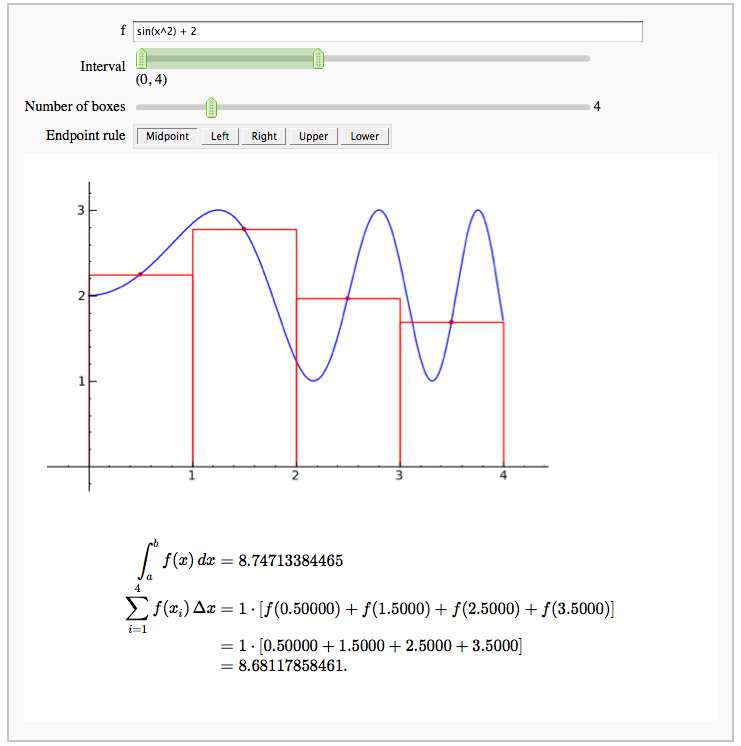
Numerical integrals with various rules
by Nick Alexander (based on the work of Marshall Hampton)
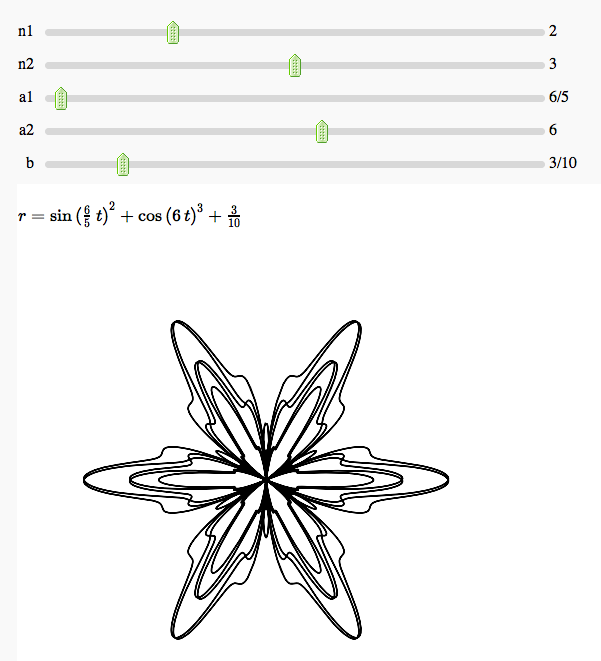
Some polar parametric curves
by Marshall Hampton. This is not very general, but could be modified to show other families of polar curves.
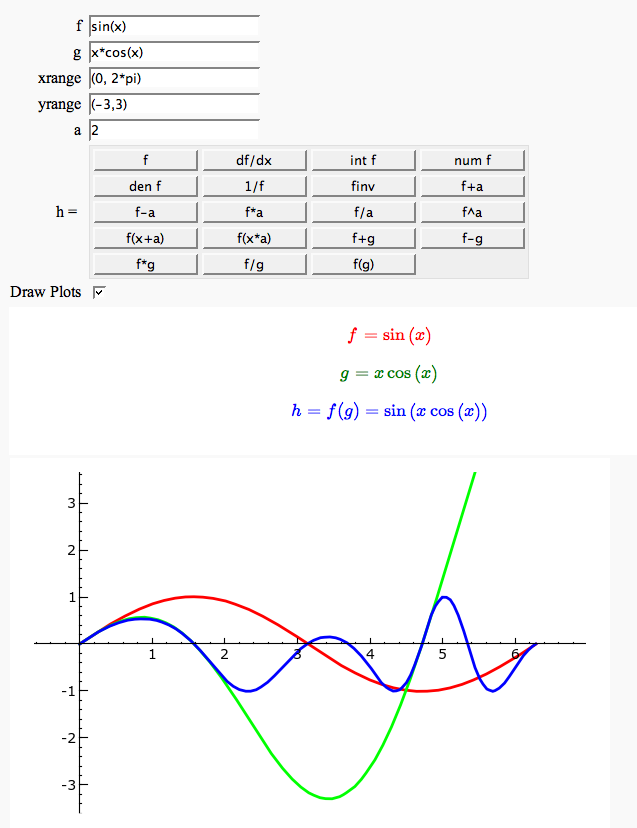
Function tool
Enter symbolic functions f, g, and a, a range, then click the appropriate button to compute and plot some combination of f, g, and a along with f and g. This is inspired by the Matlab funtool GUI.
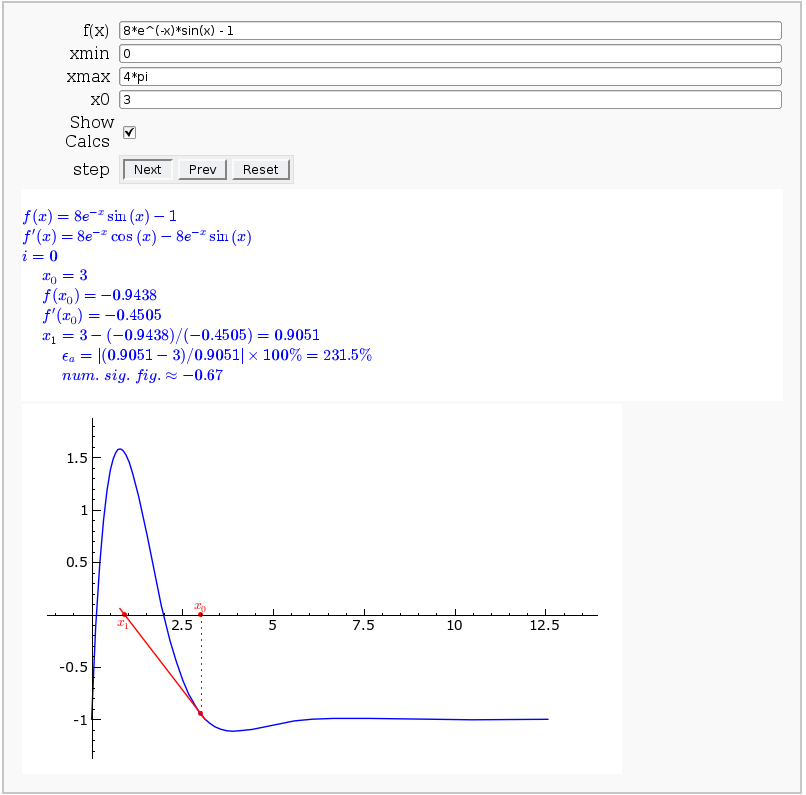
Newton-Raphson Root Finding
by Neal Holtz
This allows user to display the Newton-Raphson procedure one step at a time. It uses the heuristic that, if any of the values of the controls change, then the procedure should be re-started, else it should be continued.
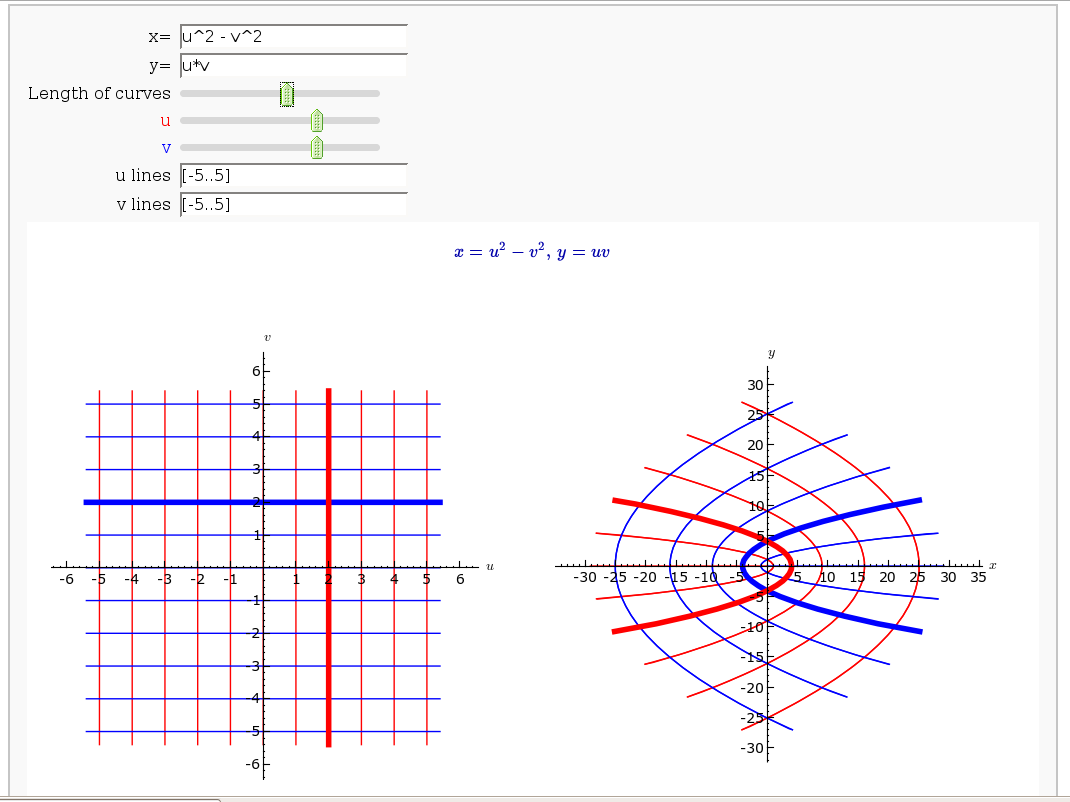
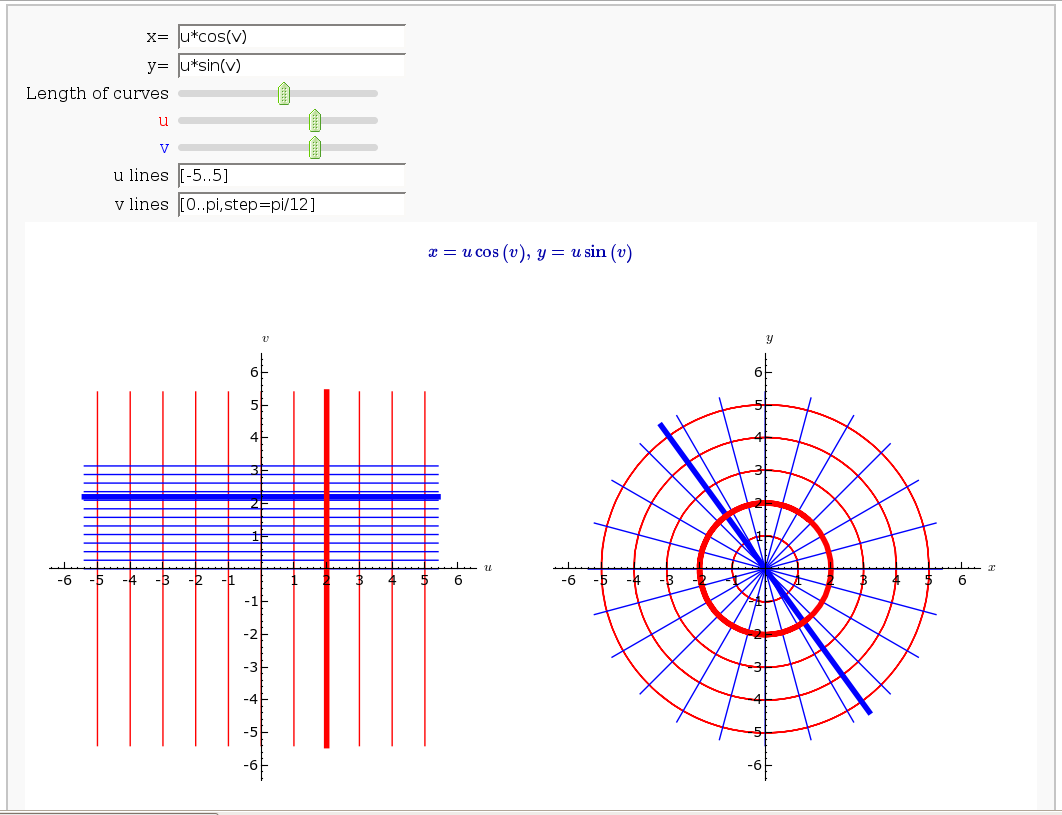
Coordinate Transformations (FIXME in Jupyter)
by Jason Grout
Taylor Series
by Harald Schilly
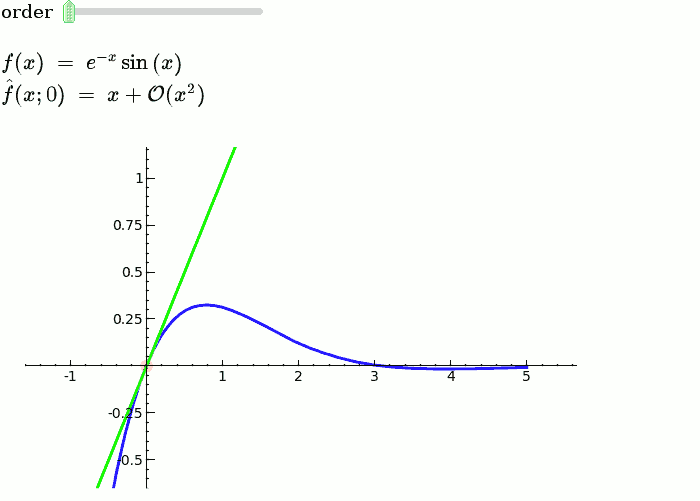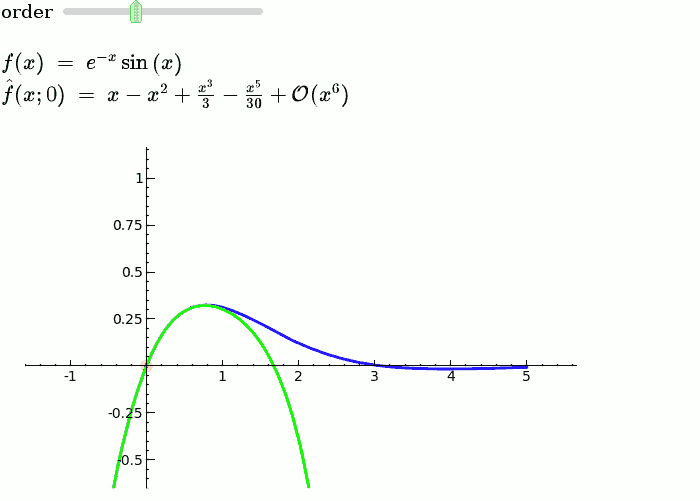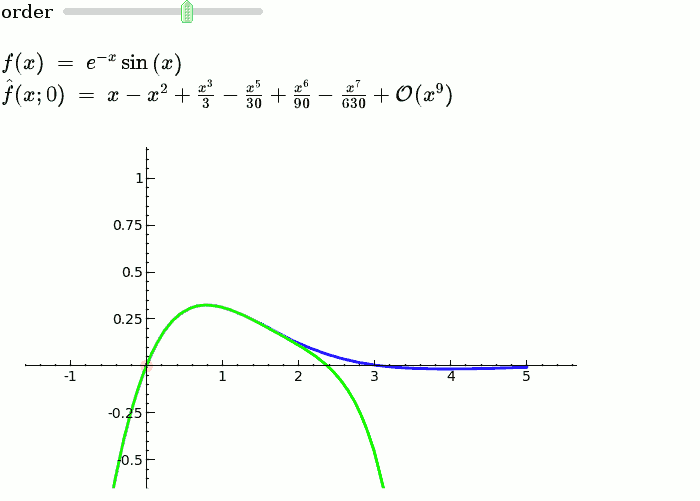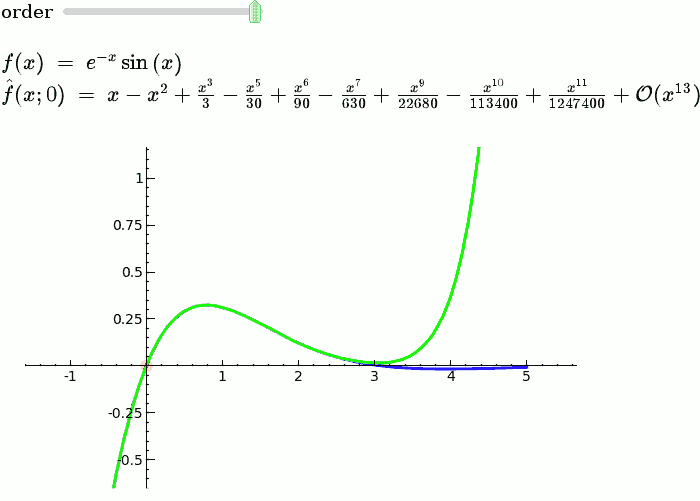
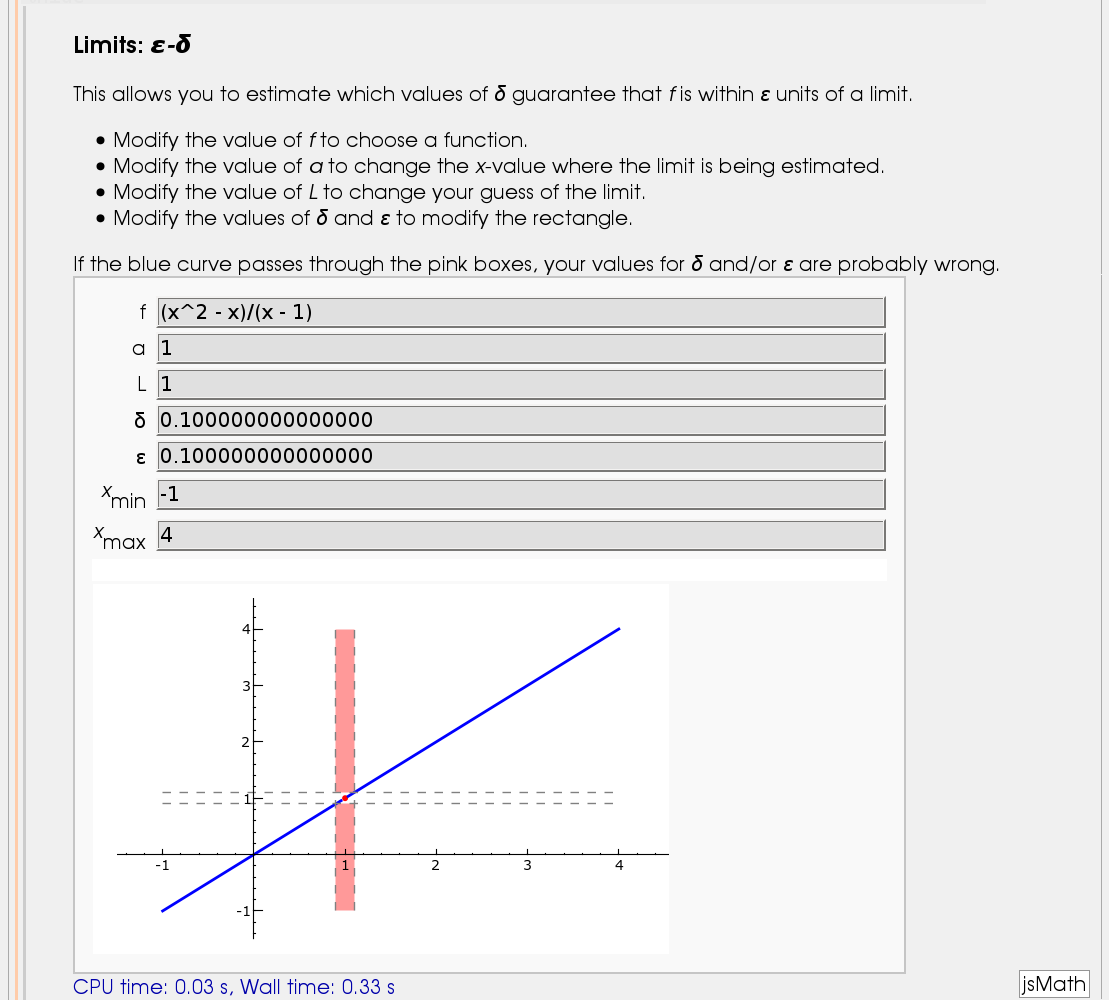
Illustration of the precise definition of a limit
by John Perry
I'll break tradition and put the image first. Apologies if this is Not A Good Thing.
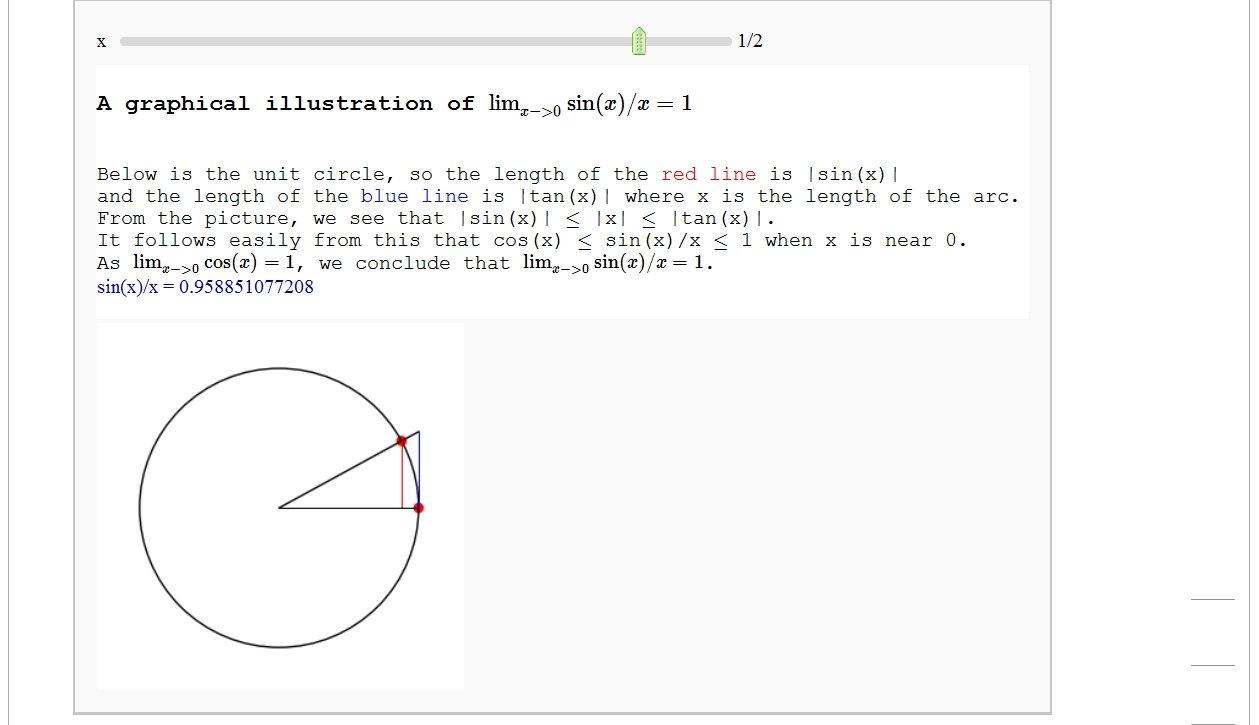
A graphical illustration of sin(x)/x -> 1 as x-> 0
by Wai Yan Pong
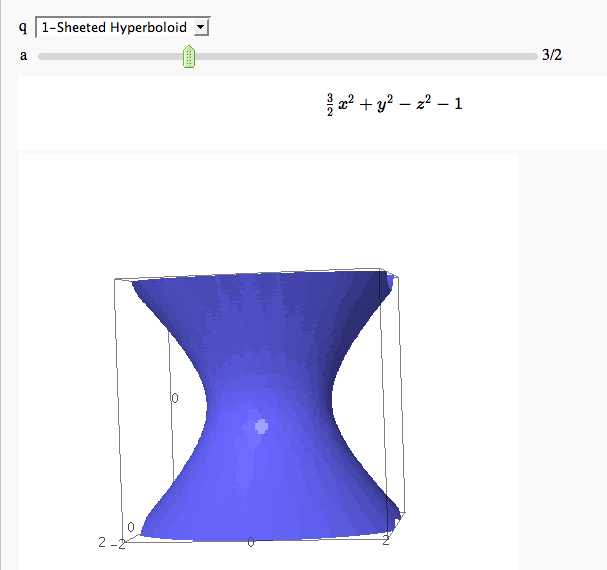
Quadric Surface Plotter
by Marshall Hampton. This is pretty simple, so I encourage people to spruce it up. In particular, it isn't set up to show all possible types of quadrics.
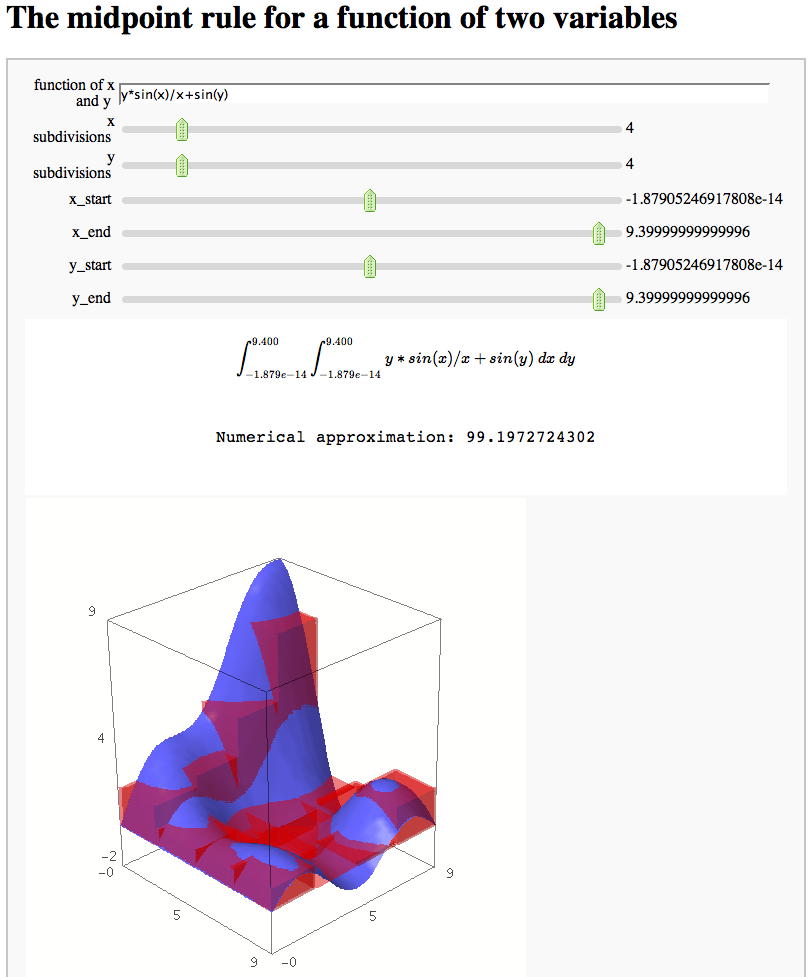
The midpoint rule for numerically integrating a function of two variables
by Marshall Hampton
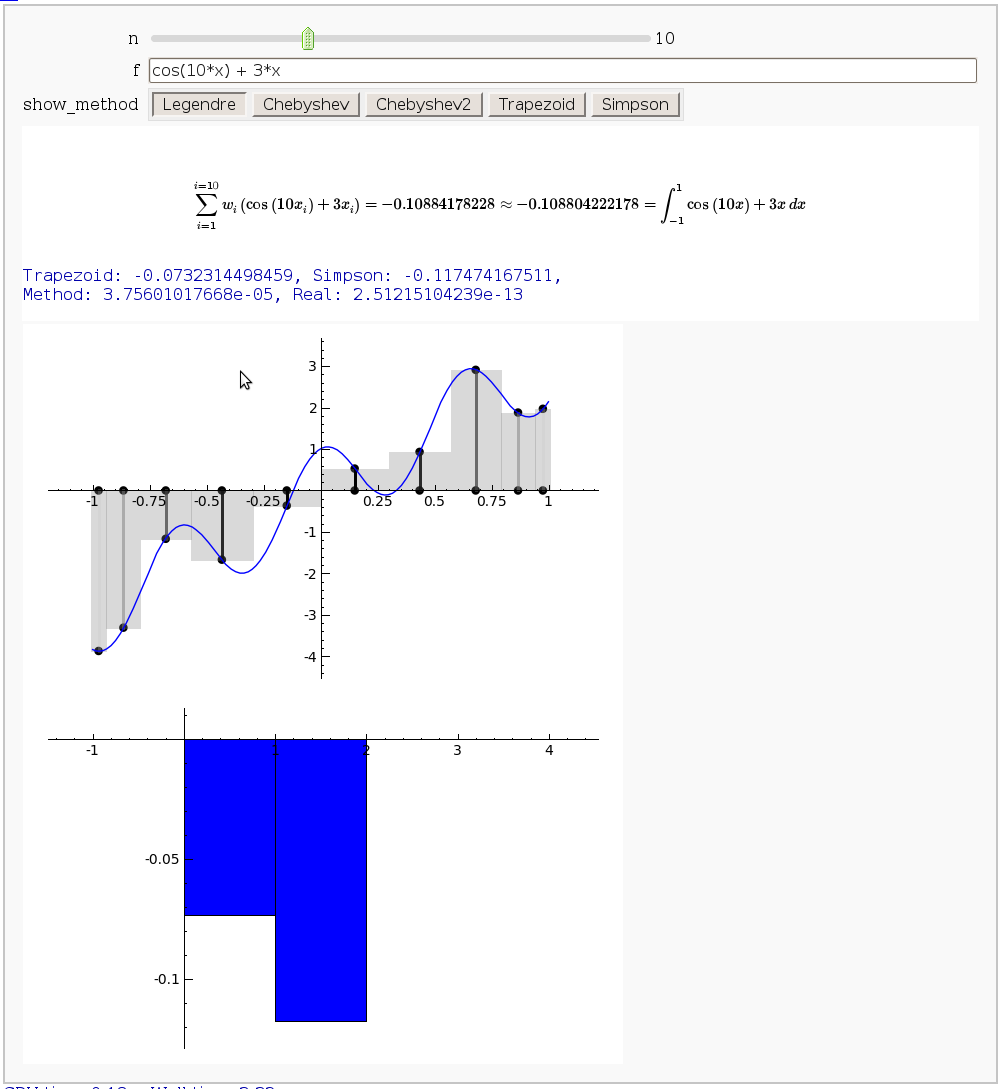
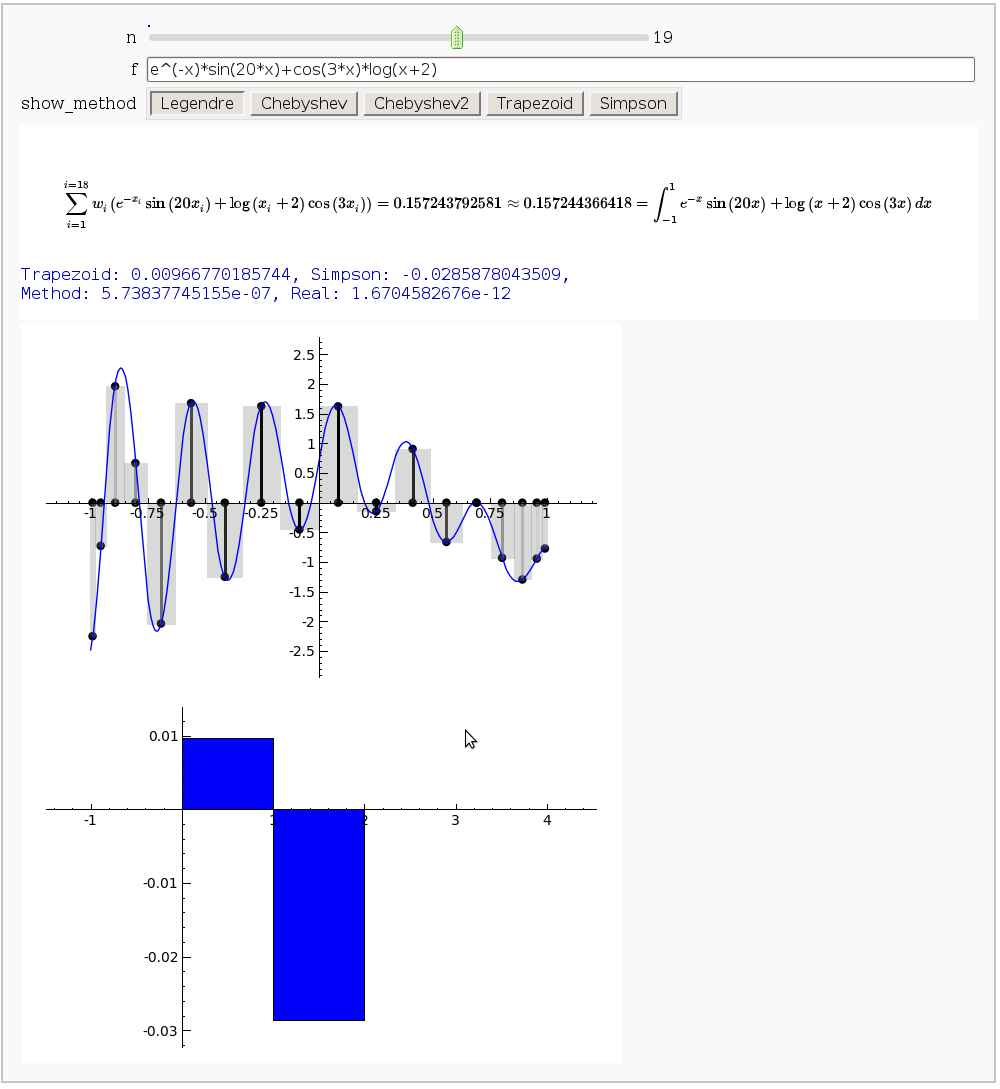
Gaussian (Legendre) quadrature
by Jason Grout
The output shows the points evaluated using Gaussian quadrature (using a weight of 1, so using Legendre polynomials). The vertical bars are shaded to represent the relative weights of the points (darker = more weight). The error in the trapezoid, Simpson, and quadrature methods is both printed out and compared through a bar graph. The "Real" error is the error returned from scipy on the definite integral.
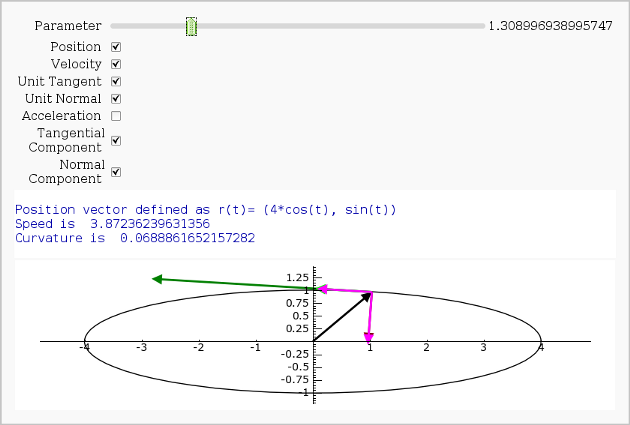
Vector Calculus, 2-D Motion
By Rob Beezer
A fast_float() version is available in a worksheet
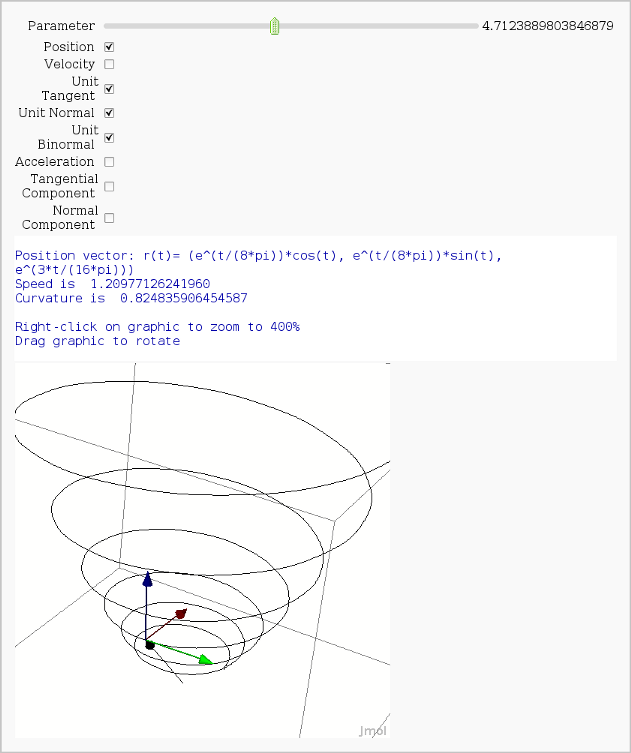
Vector Calculus, 3-D Motion (FIXME)
by Rob Beezer
Available as a worksheet
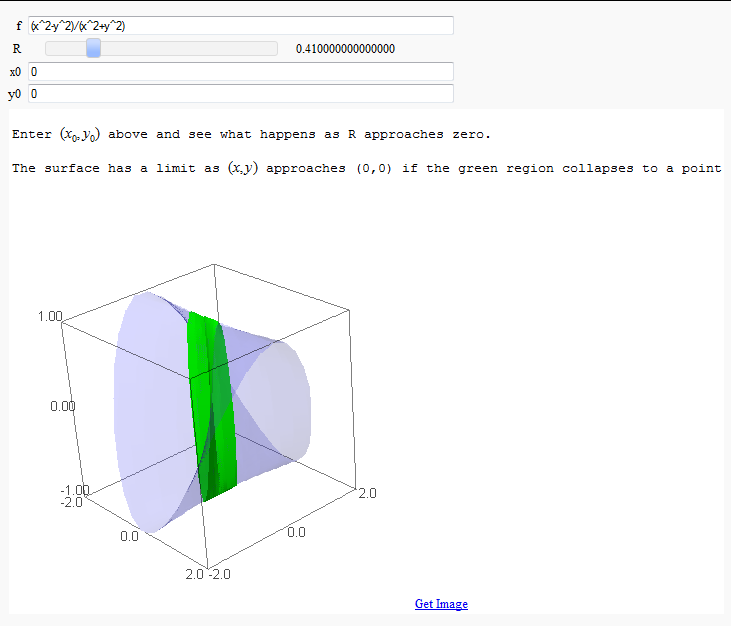
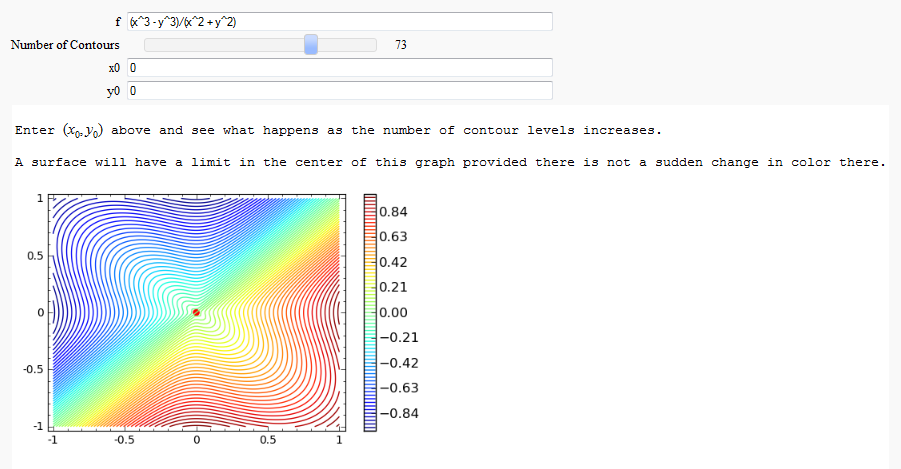
Multivariate Limits by Definition
by John Travis
http://sagenb.mc.edu/home/pub/97/
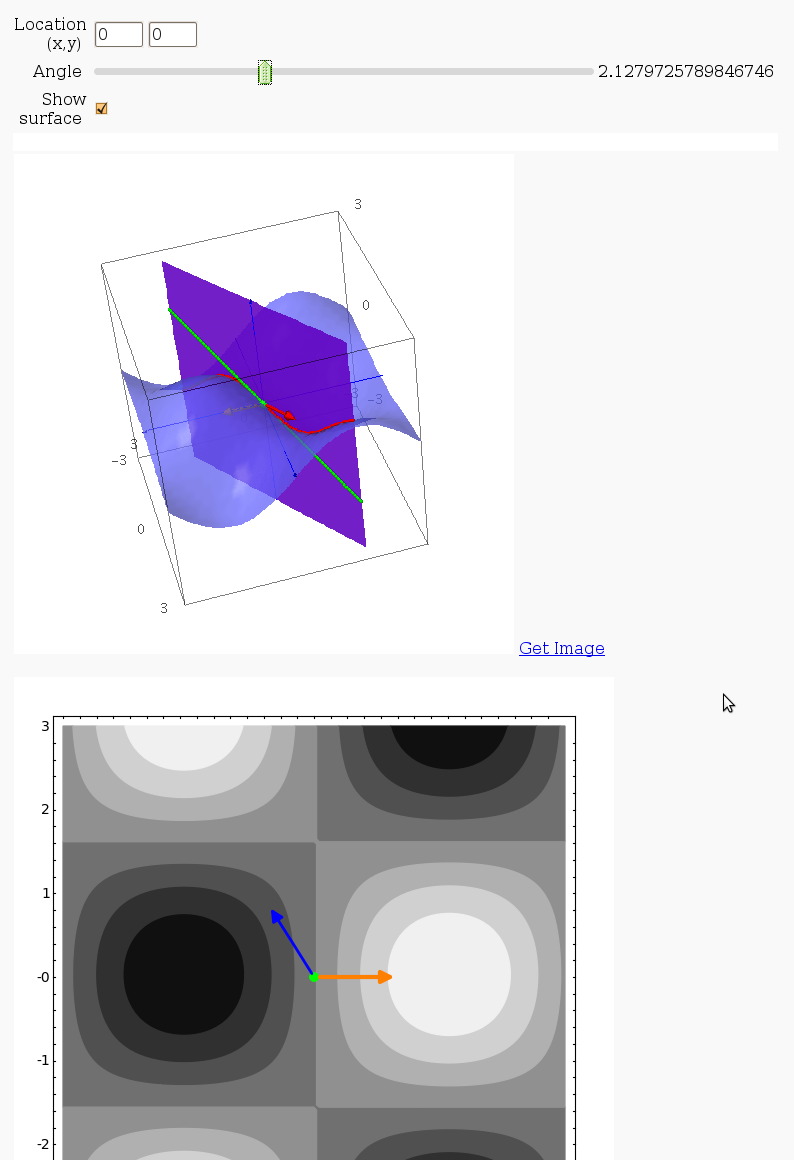
Directional Derivatives
This interact displays graphically a tangent line to a function, illustrating a directional derivative (the slope of the tangent line).
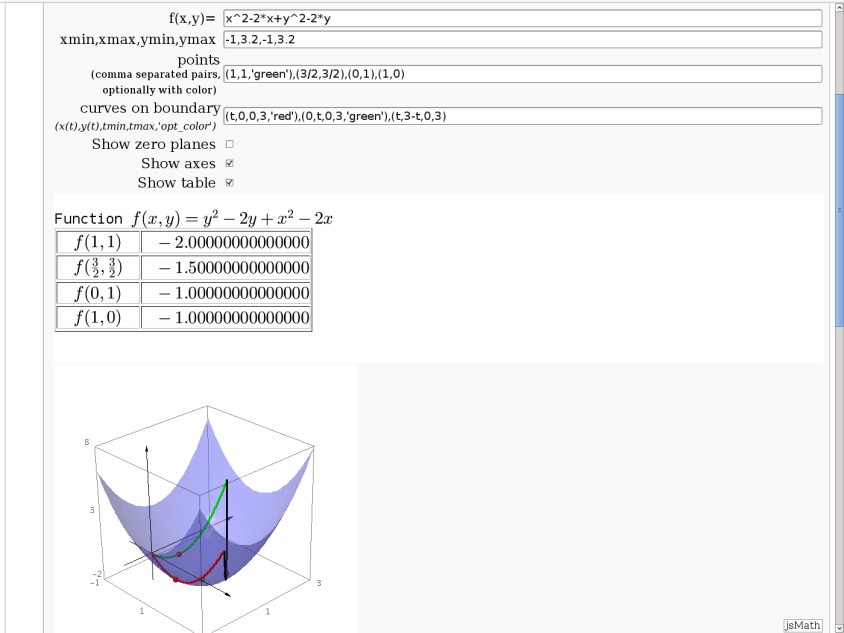
3D graph with points and curves
By Robert Marik
This sagelet is handy when showing local, constrained and absolute maxima and minima in two variables. Available as a worksheet
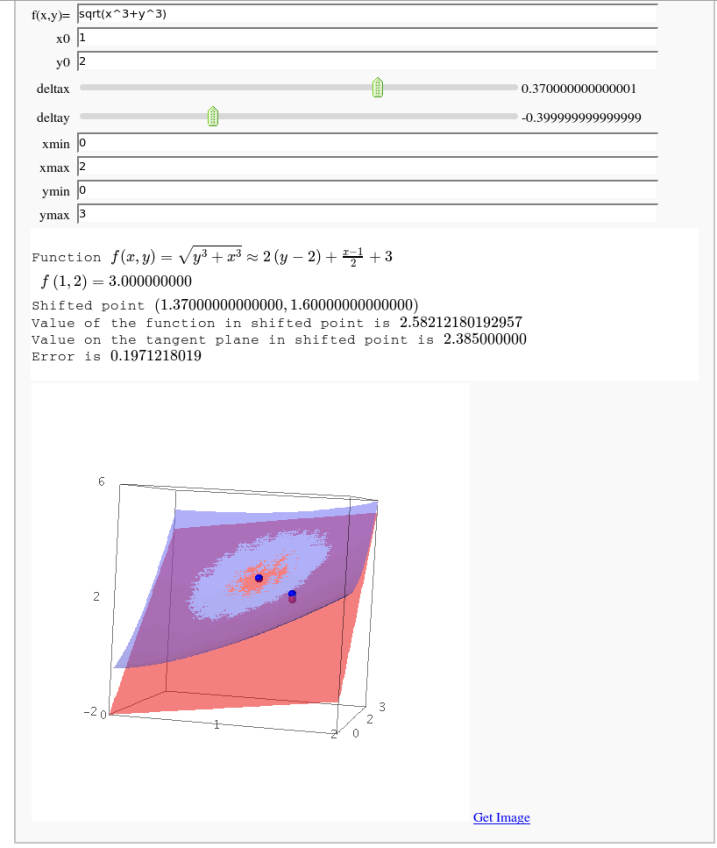
Approximating function in two variables by differential
by Robert Marik
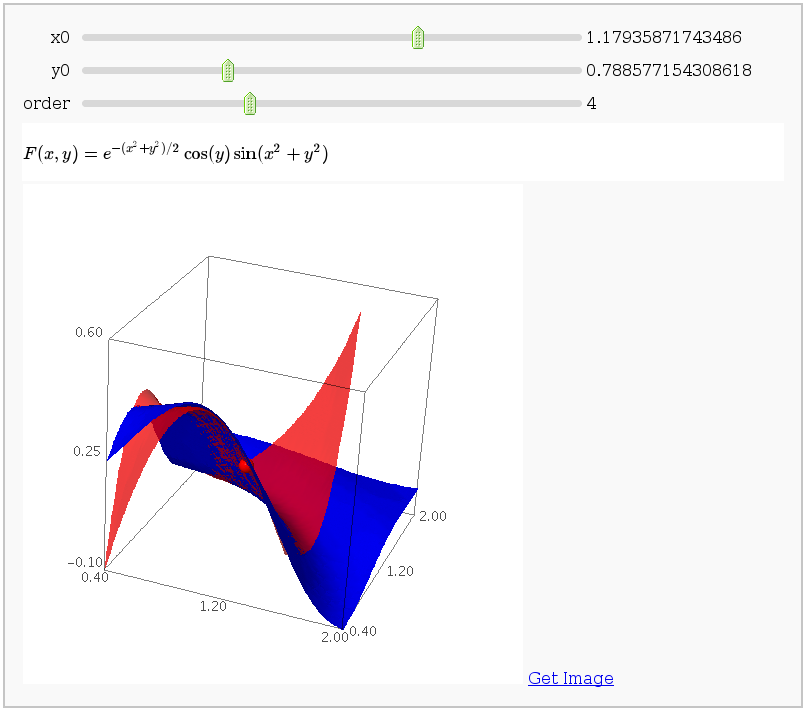
Taylor approximations in two variables
by John Palmieri
This displays the nth order Taylor approximation, for n from 1 to 10, of the function sin(x2 + y2) cos(y) exp(-(x2+y2)/2).
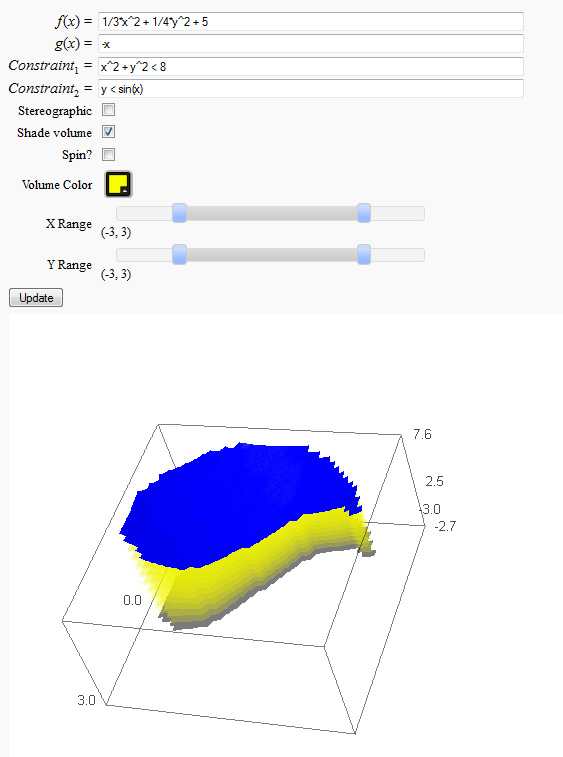
Volumes over non-rectangular domains
by John Travis
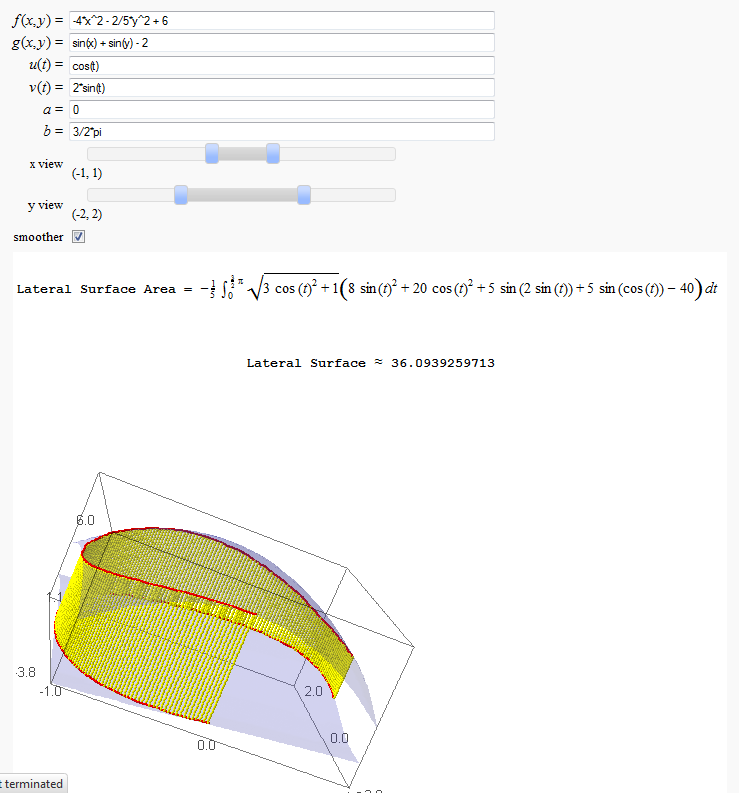
Lateral Surface Area (FIXME in Jupyter)
by John Travis
http://sagenb.mc.edu/home/pub/89/
Parametric surface example (FIXME in Jupyter)
by Marshall Hampton
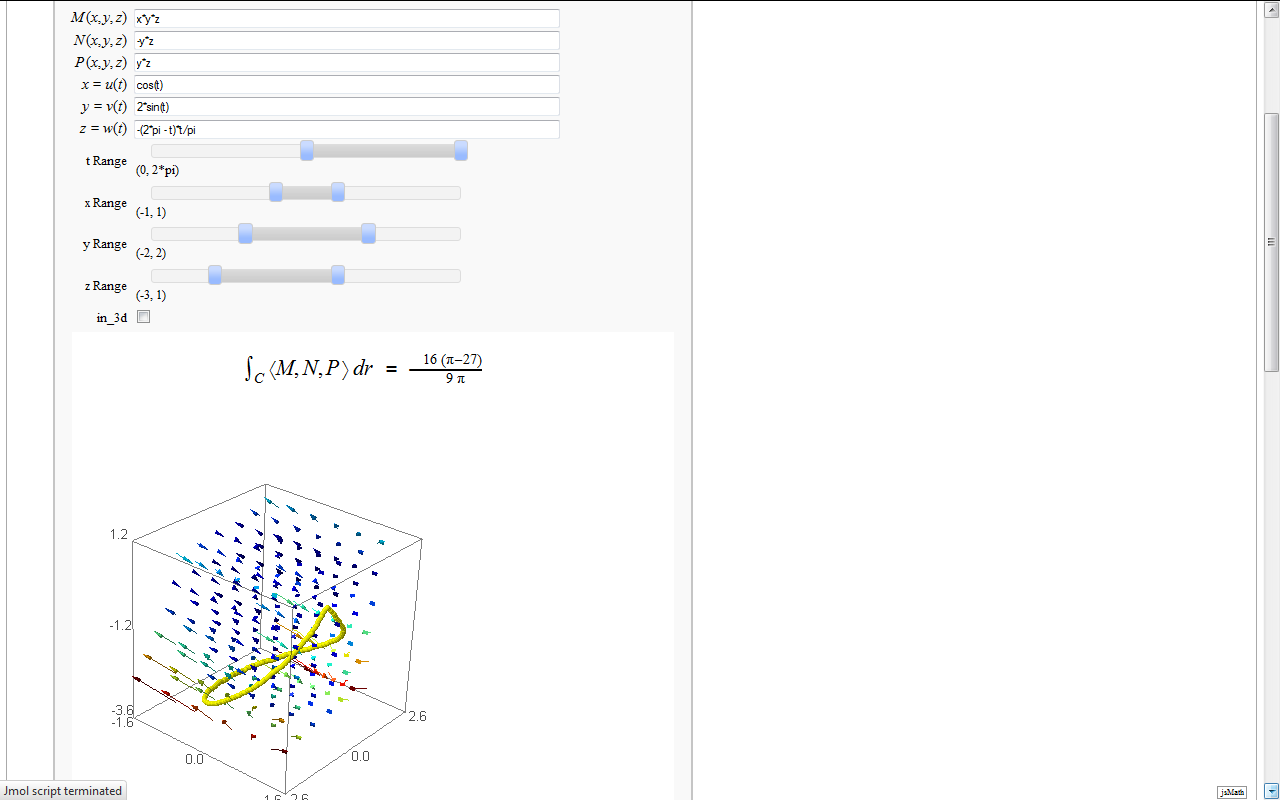
Line Integrals in 3D Vector Field
by John Travis