|
Size: 57675
Comment: Five derivatives now explicity with respect to t
|
← Revision 117 as of 2020-08-11 14:10:09 ⇥
Size: 63144
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 27: | Line 27: |
| raise ValueError, "f must have a sign change in the interval (%s,%s)"%(a,b) | raise ValueError("f must have a sign change in the interval (%s,%s)"%(a,b)) |
| Line 29: | Line 29: |
| html("<h1>Double Precision Root Finding Using Bisection</h1>") @interact def _(f = cos(x) - x, a = float(0), b = float(1), eps=(-3,(-16..-1))): |
pretty_print(html("<h1>Double Precision Root Finding Using Bisection</h1>")) @interact def _(f = cos(x) - x, a = float(0), b = float(1), eps=(-3,(-16, -1))): |
| Line 33: | Line 33: |
| print "eps = %s"%float(eps) | print("eps = %s" % float(eps)) |
| Line 35: | Line 35: |
| time c, intervals = bisect_method(f, a, b, eps) | c, intervals = bisect_method(f, a, b, eps) |
| Line 37: | Line 37: |
| print "f must have opposite sign at the endpoints of the interval" | print("f must have opposite sign at the endpoints of the interval") |
| Line 40: | Line 40: |
| print "root =", c print "f(c) = %r"%f(c) print "iterations =", len(intervals) |
print("root =", c) print("f(c) = %r" % f(x=c)) print("iterations =", len(intervals)) |
| Line 57: | Line 57: |
| http://sagenb.org/home/pub/2824/ | https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2824-Double%20Precision%20Root%20Finding%20Using%20Newton's%20Method.sagews |
| Line 69: | Line 69: |
| for i in xrange(maxiter): | for i in range(maxiter): |
| Line 77: | Line 77: |
| html("<h1>Double Precision Root Finding Using Newton's Method</h1>") @interact def _(f = x^2 - 2, c = float(0.5), eps=(-3,(-16..-1)), interval=float(0.5)): |
pretty_print(html("<h1>Double Precision Root Finding Using Newton's Method</h1>")) @interact def _(f = x^2 - 2, c = float(0.5), eps=(-3,(-16, -1)), interval=float(0.5)): |
| Line 81: | Line 81: |
| print "eps = %s"%float(eps) time z, iterates = newton_method(f, c, eps) print "root =", z print "f(c) = %r"%f(x=z) |
print("eps = %s"%float(eps)) z, iterates = newton_method(f, c, eps) print("root = {}".format(z)) print("f(c) = %r" % f(x=z)) |
| Line 86: | Line 86: |
| print "iterations =", n html(iterates) |
print("iterations = {}".format(n)) pretty_print(html(iterates)) |
| Line 99: | Line 99: |
| http://sagenb.org/home/pub/2823/ | https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2823.sagews |
| Line 118: | Line 118: |
| html('<h2>Tangent line grapher</h2>') | pretty_print(html('<h2>Tangent line grapher</h2>')) |
| Line 125: | Line 125: |
| tanf = f(x0i) + df(x0i)*(x-x0i) | tanf = f(x=x0i) + df(x=x0i)*(x-x0i) |
| Line 127: | Line 127: |
| print 'Tangent line is y = ' + tanf._repr_() | print('Tangent line is y = ' + tanf._repr_()) |
| Line 129: | Line 129: |
| fmax = f.find_maximum_on_interval(prange[0], prange[1])[0] fmin = f.find_minimum_on_interval(prange[0], prange[1])[0] |
fmax = f.find_local_maximum(prange[0], prange[1])[0] fmin = f.find_local_minimum(prange[0], prange[1])[0] |
| Line 146: | Line 146: |
| midys = [func(x_val) for x_val in midxs] | midys = [func(x=x_val) for x_val in midxs] |
| Line 152: | Line 152: |
| min_y = find_minimum_on_interval(func,a,b)[0] max_y = find_maximum_on_interval(func,a,b)[0] html('<h3>Numerical integrals with the midpoint rule</h3>') html('$\int_{a}^{b}{f(x) dx} {\\approx} \sum_i{f(x_i) \Delta x}$') print "\n\nSage numerical answer: " + str(integral_numerical(func,a,b,max_points = 200)[0]) print "Midpoint estimated answer: " + str(RDF(dx*sum([midys[q] for q in range(n)]))) |
min_y = min(0, find_local_minimum(func,a,b)[0]) max_y = max(0, find_local_maximum(func,a,b)[0]) pretty_print(html('<h3>Numerical integrals with the midpoint rule</h3>')) pretty_print(html(r'$\int_{a}^{b}{f(x) dx} {\approx} \sum_i{f(x_i) \Delta x}$')) print("\n\nSage numerical answer: " + str(integral_numerical(func,a,b,max_points = 200)[0])) print("Midpoint estimated answer: " + str(RDF(dx*sum([midys[q] for q in range(n)])))) |
| Line 166: | Line 166: |
| # by Nick Alexander (based on the work of Marshall Hampton) |
|
| Line 176: | Line 174: |
| t = sage.calculus.calculus.var('t') | t = var('t') |
| Line 190: | Line 188: |
| x = find_maximum_on_interval(func, q*dx + a, q*dx + dx + a)[1] | x = find_local_maximum(func, q*dx + a, q*dx + dx + a)[1] |
| Line 193: | Line 191: |
| x = find_minimum_on_interval(func, q*dx + a, q*dx + dx + a)[1] | x = find_local_minimum(func, q*dx + a, q*dx + dx + a)[1] |
| Line 204: | Line 202: |
| min_y = min(0, find_minimum_on_interval(func,a,b)[0]) max_y = max(0, find_maximum_on_interval(func,a,b)[0]) # html('<h3>Numerical integrals with the midpoint rule</h3>') |
min_y = min(0, find_local_minimum(func,a,b)[0]) max_y = max(0, find_local_maximum(func,a,b)[0]) pretty_print(html('<h3>Numerical integral with the {} rule</h3>'.format(endpoint_rule))) |
| Line 215: | Line 213: |
| sum_html = "%s \cdot \\left[ %s \\right]" % (dx, ' + '.join([ "f(%s)" % cap(i) for i in xs ])) num_html = "%s \cdot \\left[ %s \\right]" % (dx, ' + '.join([ str(cap(i)) for i in ys ])) |
sum_html = "%s \\cdot \\left[ %s \\right]" % (dx, ' + '.join([ "f(%s)" % cap(i) for i in xs ])) num_html = "%s \\cdot \\left[ %s \\right]" % (dx, ' + '.join([ str(cap(i)) for i in ys ])) |
| Line 221: | Line 219: |
| html(r''' <div class="math"> \begin{align*} \int_{a}^{b} {f(x) \, dx} & = %s \\\ \sum_{i=1}^{%s} {f(x_i) \, \Delta x} & = %s \\\ & = %s \\\ & = %s . \end{align*} </div> ''' % (numerical_answer, number_of_subdivisions, sum_html, num_html, estimated_answer)) |
pretty_print(html(r''' <div class="math"> \begin{align*} \int_{a}^{b} {f(x) \, dx} & = %s \\\ \sum_{i=1}^{%s} {f(x_i) \, \Delta x} & = %s \\\ & = %s \\\ & = %s . \end{align*} </div>''' % (numerical_answer, number_of_subdivisions, sum_html, num_html, estimated_answer))) |
| Line 242: | Line 237: |
| html('$r=' + latex(b+sin(a1*t)^n1 + cos(a2*t)^n2)+'$') | pretty_print(html('$r=' + latex(b+sin(a1*t)^n1 + cos(a2*t)^n2)+'$')) |
| Line 262: | Line 257: |
| except TypeError, msg: print msg[-200:] print "Unable to make sense of f,g, or a as symbolic expressions." |
except TypeError as msg: print(msg[-200:]) print("Unable to make sense of f,g, or a as symbolic expressions.") |
| Line 329: | Line 324: |
| html('<center><font color="red">$f = %s$</font></center>'%latex(f)) html('<center><font color="green">$g = %s$</font></center>'%latex(g)) html('<center><font color="blue"><b>$h = %s = %s$</b></font></center>'%(lbl, latex(h))) |
pretty_print(html('<center><font color="red">$f = %s$</font></center>'%latex(f))) pretty_print(html('<center><font color="green">$g = %s$</font></center>'%latex(g))) pretty_print(html('<center><font color="blue"><b>$h = %s = %s$</b></font></center>'%(lbl, latex(h)))) |
| Line 379: | Line 374: |
| vertical_alignment="bottom" if f(x0) < 0 else "top" ) | vertical_alignment="bottom" if f(x=x0) < 0 else "top" ) |
| Line 395: | Line 390: |
| fi = RR(f(xi)) fpi = RR(df(xi)) |
fi = RR(f(x=xi)) fpi = RR(df(x=xi)) |
| Line 431: | Line 426: |
| vertical_alignment="bottom" if f(xip1) < 0 else "top" ) | vertical_alignment="bottom" if f(x=xip1) < 0 else "top" ) |
| Line 447: | Line 442: |
| html( t ) | pretty_print(html( t )) |
| Line 457: | Line 452: |
| # polar coordinates #(x,y)=(u*cos(v),u*sin(v)); (u_range,v_range)=([0..6],[0..2*pi,step=pi/12]) # weird example (x,y)=(u^2-v^2,u*v+cos(u*v)); (u_range,v_range)=([-5..5],[-5..5]) thickness=4 square_length=.05 |
|
| Line 460: | Line 464: |
| def trans(x=input_box(u^2-v^2, label="x=",type=SR), \ y=input_box(u*v+cos(u*v), label="y=",type=SR), \ t_val=slider(0,10,0.2,6, label="Length of curves"), \ u_percent=slider(0,1,0.05,label="<font color='red'>u</font>", default=.7), v_percent=slider(0,1,0.05,label="<font color='blue'>v</font>", default=.7), u_range=input_box(range(-5,5,1), label="u lines"), v_range=input_box(range(-5,5,1), label="v lines")): thickness=4 u_val = min(u_range)+(max(u_range)-min(u_range))*u_percent v_val = min(v_range)+(max(v_range)-min(v_range))*v_percent t_min = -t_val t_max = t_val g1=sum([parametric_plot((i,v), (v,t_min,t_max), rgbcolor=(1,0,0)) for i in u_range]) g2=sum([parametric_plot((u,i), (u,t_min,t_max), rgbcolor=(0,0,1)) for i in v_range]) vline_straight=parametric_plot((u,v_val), (u,t_min,t_max), rgbcolor=(0,0,1), linestyle='-',thickness=thickness) uline_straight=parametric_plot((u_val, v), (v,t_min,t_max),rgbcolor=(1,0,0), linestyle='-',thickness=thickness) (g1+g2+vline_straight+uline_straight).save("uv_coord.png",aspect_ratio=1, figsize=[5,5], axes_labels=['$u$','$v$']) xuv = fast_float(x,'u','v') yuv = fast_float(y,'u','v') xvu = fast_float(x,'v','u') yvu = fast_float(y,'v','u') g3=sum([parametric_plot((partial(xuv,i),partial(yuv,i)), (v,t_min,t_max), rgbcolor=(1,0,0)) for i in u_range]) g4=sum([parametric_plot((partial(xvu,i),partial(yvu,i)), (u,t_min,t_max), rgbcolor=(0,0,1)) for i in v_range]) uline=parametric_plot((partial(xuv,u_val),partial(yuv,u_val)),(v,t_min,t_max),rgbcolor=(1,0,0), linestyle='-',thickness=thickness) vline=parametric_plot((partial(xvu,v_val),partial(yvu,v_val)), (u,t_min,t_max), rgbcolor=(0,0,1), linestyle='-',thickness=thickness) (g3+g4+vline+uline).save("xy_coord.png", aspect_ratio=1, figsize=[5,5], axes_labels=['$x$','$y$']) print jsmath("x=%s, \: y=%s"%(latex(x), latex(y))) print "<html><table><tr><td><img src='cell://uv_coord.png'/></td><td><img src='cell://xy_coord.png'/></td></tr></table></html>" |
def trans(x=input_box(x, label="x",type=SR), y=input_box(y, label="y",type=SR), u_percent=slider(0,1,0.05,label="u", default=.7), v_percent=slider(0,1,0.05,label="v", default=.7), t_val=slider(0,10,0.2,6, label="Length"), u_range=input_box(u_range, label="u lines"), v_range=input_box(v_range, label="v lines")): x(u,v)=x y(u,v)=y u_val = min(u_range)+(max(u_range)-min(u_range))*u_percent v_val = min(v_range)+(max(v_range)-min(v_range))*v_percent t_min = -t_val t_max = t_val uvplot=sum([parametric_plot((i,v), (v,t_min,t_max), color='red',axes_labels=['u','v'],figsize=[5,5]) for i in u_range]) uvplot+=sum([parametric_plot((u,i), (u,t_min,t_max), color='blue',axes_labels=['u','v']) for i in v_range]) uvplot+=parametric_plot((u,v_val), (u,t_min,t_max), rgbcolor=(0,0,1), linestyle='-',thickness=thickness) uvplot+=parametric_plot((u_val, v), (v,t_min,t_max),rgbcolor=(1,0,0), linestyle='-',thickness=thickness) pt=vector([u_val,v_val]) du=vector([(t_max-t_min)*square_length,0]) dv=vector([0,(t_max-t_min)*square_length]) uvplot+=polygon([pt,pt+dv,pt+du+dv,pt+du],color='purple',alpha=0.7) uvplot+=line([pt,pt+dv,pt+du+dv,pt+du],color='green') T(u,v)=(x,y) xuv = fast_float(x,'u','v') yuv = fast_float(y,'u','v') xvu = fast_float(x,'v','u') yvu = fast_float(y,'v','u') xyplot=sum([parametric_plot((partial(xuv,i),partial(yuv,i)), (v,t_min,t_max), color='red', axes_labels=['x','y'],figsize=[5,5]) for i in u_range]) xyplot+=sum([parametric_plot((partial(xvu,i),partial(yvu,i)), (u,t_min,t_max), color='blue') for i in v_range]) xyplot+=parametric_plot((partial(xuv,u_val),partial(yuv,u_val)),(v,t_min,t_max),color='red', linestyle='-',thickness=thickness) xyplot+=parametric_plot((partial(xvu,v_val),partial(yvu,v_val)), (u,t_min,t_max), color='blue', linestyle='-',thickness=thickness) jacobian(u,v)=abs(T.diff().det()).simplify_full() t_vals=[0..1,step=t_val*.01] vertices=[(x(*c),y(*c)) for c in [pt+t*dv for t in t_vals]] vertices+=[(x(*c),y(*c)) for c in [pt+dv+t*du for t in t_vals]] vertices+=[(x(*c),y(*c)) for c in [pt+(1-t)*dv+du for t in t_vals]] vertices+=[(x(*c),y(*c)) for c in [pt+(1-t)*du for t in t_vals]] xyplot+=polygon(vertices,color='purple',alpha=0.7) xyplot+=line(vertices,color='green') pretty_print(html("$T(u,v)=%s$"%(latex(T(u,v))))) pretty_print(html("Jacobian: $%s$"%latex(jacobian(u,v)))) pretty_print(html("A very small region in $xy$ plane is approximately %0.4g times the size of the corresponding region in the $uv$ plane"%jacobian(u_val,v_val).n())) show(graphics_array([uvplot,xyplot])) |
| Line 502: | Line 522: |
| dot = point((x0,f(x0)),pointsize=80,rgbcolor=(1,0,0)) @interact def _(order=(1..12)): |
dot = point((x0,f(x=x0)),pointsize=80,rgbcolor=(1,0,0)) @interact def _(order=[1..12]): |
| Line 507: | Line 527: |
| html('$f(x)\;=\;%s$'%latex(f)) html('$\hat{f}(x;%s)\;=\;%s+\mathcal{O}(x^{%s})$'%(x0,latex(ft),order+1)) |
pretty_print(html(r'$f(x)\;=\;%s$'%latex(f))) pretty_print(html(r'$\hat{f}(x;%s)\;=\;%s+\mathcal{O}(x^{%s})$'%(x0,latex(ft),order+1))) |
| Line 521: | Line 541: |
| html("<h2>Limits: <i>ε-δ</i></h2>") html("This allows you to estimate which values of <i>δ</i> guarantee that <i>f</i> is within <i>ε</i> units of a limit.") html("<ul><li>Modify the value of <i>f</i> to choose a function.</li>") html("<li>Modify the value of <i>a</i> to change the <i>x</i>-value where the limit is being estimated.</li>") html("<li>Modify the value of <i>L</i> to change your guess of the limit.</li>") html("<li>Modify the values of <i>δ</i> and <i>ε</i> to modify the rectangle.</li></ul>") html("If the blue curve passes through the pink boxes, your values for <i>δ</i> and/or <i>ε</i> are probably wrong.") @interact def delta_epsilon(f = input_box(default=(x^2-x)/(x-1)), a=input_box(default=1), L = input_box(default=1), delta=input_box(label="δ",default=0.1), epsilon=input_box(label="ε",default=0.1), xm=input_box(label="<i>x</i><sub>min</sub>",default=-1), xM=input_box(label="<i>x</i><sub>max</sub>",default=4)): |
pretty_print(html("<h2>Limits: <i>ε-δ</i></h2>")) pretty_print(html("This allows you to estimate which values of <i>δ</i> guarantee that <i>f</i> is within <i>ε</i> units of a limit.")) pretty_print(html("<ul><li>Modify the value of <i>f</i> to choose a function.</li>")) pretty_print(html("<li>Modify the value of <i>a</i> to change the <i>x</i>-value where the limit is being estimated.</li>")) pretty_print(html("<li>Modify the value of <i>L</i> to change your guess of the limit.</li>")) pretty_print(html("<li>Modify the values of <i>δ</i> and <i>ε</i> to modify the rectangle.</li></ul>")) pretty_print(html("If the blue curve passes through the pink boxes, your values for <i>δ</i> and/or <i>ε</i> are probably wrong.")) @interact def delta_epsilon(f = input_box(default=(x^2-x)/(x-1), label="$f$"), a=input_box(default=1, label="$a$"), L = input_box(default=1, label="$L$"), delta=input_box(label=r"$\delta$",default=0.1), epsilon=input_box(label=r"$\varepsilon$",default=0.1), xm=input_box(label=r"$x_{min}$",default=-1), xM=input_box(label=r"$x_{max}$",default=4)): |
| Line 551: | Line 571: |
| html('<h3>A graphical illustration of $\lim_{x -> 0} \sin(x)/x =1$</h3>') html('Below is the unit circle, so the length of the <font color=red>red line</font> is |sin(x)|') html('and the length of the <font color=blue>blue line</font> is |tan(x)| where x is the length of the arc.') html('From the picture, we see that |sin(x)| $\le$ |x| $\le$ |tan(x)|.') html('It follows easily from this that cos(x) $\le$ sin(x)/x $\le$ 1 when x is near 0.') html('As $\lim_{x ->0} \cos(x) =1$, we conclude that $\lim_{x -> 0} \sin(x)/x =1$.') |
pretty_print(html(r'<h3>A graphical illustration of $\lim_{x -> 0} \sin(x)/x =1$</h3>')) pretty_print(html(r'Below is the unit circle, so the length of the <font color=red>red line</font> is |sin(x)|')) pretty_print(html(r'and the length of the <font color=blue>blue line</font> is |tan(x)| where x is the length of the arc.')) pretty_print(html(r'From the picture, we see that |sin(x)| $\le$ |x| $\le$ |tan(x)|.')) pretty_print(html(r'It follows easily from this that cos(x) $\le$ sin(x)/x $\le$ 1 when x is near 0.')) pretty_print(html(r'As $\lim_{x ->0} \cos(x) =1$, we conclude that $\lim_{x -> 0} \sin(x)/x =1$.')) |
| Line 577: | Line 597: |
| def quads(q = selector(quadrics.keys()), a = slider(0,5,1/2,default = 1)): | def quads(q = selector(list(quadrics)), a = slider(0,5,1/2,default = 1)): |
| Line 579: | Line 599: |
| if a==0 or q=='Cone': html('<center>$'+latex(f)+' \ $'+ '(degenerate)</center>') else: html('<center>$'+latex(f)+'$ </center>') |
if a==0 or q=='Cone': pretty_print(latex(f), " (degenerate)") else: pretty_print(latex(f)) |
| Line 607: | Line 627: |
| sin,cos = math.sin,math.cos html("<h1>The midpoint rule for a function of two variables</h1>") |
pretty_print(html(r"<h1>The midpoint rule for a function of two variables</h1>")) |
| Line 623: | Line 643: |
| html("$$\int_{"+str(R16(y_start))+"}^{"+str(R16(y_end))+"} "+ "\int_{"+str(R16(x_start))+"}^{"+str(R16(x_end))+"} "+func+"\ dx \ dy$$") html('<p style="text-align: center;">Numerical approximation: ' + str(num_approx)+'</p>') |
pretty_print(html(r"$\int_{"+str(R16(y_start))+r"}^{"+str(R16(y_end))+r"} "+ r"\int_{"+str(R16(x_start))+r"}^{"+str(R16(x_end))+r"} "+latex(SR(func))+r"\ dx \ dy$")) pretty_print(html(r'<p style="text-align: center;">Numerical approximation: ' + str(num_approx)+r'</p>')) |
| Line 640: | Line 660: |
| from numpy import linspace | from numpy import linspace, asanyarray, diff |
| Line 692: | Line 712: |
| y_val = map(scaled_ff,x_val) | y_val = [*map(scaled_ff,x_val)] |
| Line 695: | Line 715: |
| html("$$\sum_{i=1}^{i=%s}w_i\left(%s\\right)= %s\\approx %s =\int_{-1}^{1}%s \,dx$$"%(n, latex(f), approximation, integral, latex(scaled_func))) |
pretty_print(html(r"$$\sum_{i=1}^{i=%s}w_i\left(%s\right)= %s\approx %s =\int_{-1}^{1}%s \,dx$$"%(n, latex(f), approximation, integral, latex(scaled_func)))) |
| Line 698: | Line 718: |
| print "Trapezoid: %s, Simpson: %s, \nMethod: %s, Real: %s"%tuple(error_data) | print("Trapezoid: %s, Simpson: %s, \nMethod: %s, Real: %s" % tuple(error_data)) |
| Line 736: | Line 756: |
| path = parametric_plot( position(t).list(), (t, start, stop), color = "black" ) | path = parametric_plot( position.list(), (t, start, stop), color = "black" ) |
| Line 740: | Line 760: |
| velocity = derivative( position(t) ) acceleration = derivative(velocity(t)) |
velocity = derivative(position, t) acceleration = derivative(velocity, t) |
| Line 743: | Line 763: |
| speed_deriv = derivative(speed) | speed_deriv = derivative(speed, t) |
| Line 745: | Line 765: |
| dT = derivative(tangent(t)) | dT = derivative(tangent, t) |
| Line 766: | Line 786: |
| pos_tzero = position(t0) | pos_tzero = position(t=t0) |
| Line 770: | Line 790: |
| speed_component = speed(t0) tangent_component = speed_deriv(t0) normal_component = sqrt( acceleration(t0).norm()^2 - tangent_component^2 ) |
speed_component = speed(t=t0) tangent_component = speed_deriv(t=t0) normal_component = sqrt( acceleration(t=t0).norm()^2 - tangent_component^2 ) |
| Line 778: | Line 798: |
| tan = arrow(pos_tzero, pos_tzero + tangent(t0), rgbcolor=(0,1,0) ) vel = arrow(pos_tzero, pos_tzero + velocity(t0), rgbcolor=(0,0.5,0)) nor = arrow(pos_tzero, pos_tzero + normal(t0), rgbcolor=(0.5,0,0)) acc = arrow(pos_tzero, pos_tzero + acceleration(t0), rgbcolor=(1,0,1)) tancomp = arrow(pos_tzero, pos_tzero + tangent_component*tangent(t0), rgbcolor=(1,0,1) ) norcomp = arrow(pos_tzero, pos_tzero + normal_component*normal(t0), rgbcolor=(1,0,1)) |
tan = arrow(pos_tzero, pos_tzero + tangent(t=t0), rgbcolor=(0,1,0) ) vel = arrow(pos_tzero, pos_tzero + velocity(t=t0), rgbcolor=(0,0.5,0)) nor = arrow(pos_tzero, pos_tzero + normal(t=t0), rgbcolor=(0.5,0,0)) acc = arrow(pos_tzero, pos_tzero + acceleration(t=t0), rgbcolor=(1,0,1)) tancomp = arrow(pos_tzero, pos_tzero + tangent_component*tangent(t=t0), rgbcolor=(1,0,1) ) norcomp = arrow(pos_tzero, pos_tzero + normal_component*normal(t=t0), rgbcolor=(1,0,1)) |
| Line 805: | Line 825: |
| print "Position vector defined as r(t)=", position(t) print "Speed is ", N(speed(t0)) print "Curvature is ", N(curvature) |
print("Position vector defined as r(t)={}".format(position)) print("Speed is {}".format(N(speed(t=t0)))) print("Curvature is {}".format(N(curvature))) |
| Line 837: | Line 857: |
| assume(t, 'real') | |
| Line 854: | Line 875: |
| path = parametric_plot3d( position(t).list(), (t, start, stop), color = "black" ) | path = parametric_plot3d( position.list(), (t, start, stop), color = "black" ) |
| Line 858: | Line 879: |
| velocity = derivative( position(t), t) acceleration = derivative(velocity(t), t) |
velocity = derivative( position, t) acceleration = derivative(velocity, t) |
| Line 863: | Line 884: |
| dT = derivative(tangent(t), t) | dT = derivative(tangent, t) |
| Line 866: | Line 887: |
| ## dB = derivative(binormal(t), t) | ## dB = derivative(binormal, t) |
| Line 887: | Line 908: |
| pos_tzero = position(t0) | pos_tzero = position(t=t0) |
| Line 891: | Line 912: |
| speed_component = speed(t0) tangent_component = speed_deriv(t0) normal_component = sqrt( acceleration(t0).norm()^2 - tangent_component^2 ) |
speed_component = speed(t=t0) tangent_component = speed_deriv(t=t0) normal_component = sqrt( acceleration(t=t0).norm()^2 - tangent_component^2 ) |
| Line 900: | Line 921: |
| tan = arrow3d(pos_tzero, pos_tzero + tangent(t0), rgbcolor=(0,1,0) ) vel = arrow3d(pos_tzero, pos_tzero + velocity(t0), rgbcolor=(0,0.5,0)) nor = arrow3d(pos_tzero, pos_tzero + normal(t0), rgbcolor=(0.5,0,0)) bin = arrow3d(pos_tzero, pos_tzero + binormal(t0), rgbcolor=(0,0,0.5)) acc = arrow3d(pos_tzero, pos_tzero + acceleration(t0), rgbcolor=(1,0,1)) tancomp = arrow3d(pos_tzero, pos_tzero + tangent_component*tangent(t0), rgbcolor=(1,0,1) ) norcomp = arrow3d(pos_tzero, pos_tzero + normal_component*normal(t0), rgbcolor=(1,0,1)) |
tan = arrow3d(pos_tzero, pos_tzero + tangent(t=t0), rgbcolor=(0,1,0) ) vel = arrow3d(pos_tzero, pos_tzero + velocity(t=t0), rgbcolor=(0,0.5,0)) nor = arrow3d(pos_tzero, pos_tzero + normal(t=t0), rgbcolor=(0.5,0,0)) bin = arrow3d(pos_tzero, pos_tzero + binormal(t=t0), rgbcolor=(0,0,0.5)) acc = arrow3d(pos_tzero, pos_tzero + acceleration(t=t0), rgbcolor=(1,0,1)) tancomp = arrow3d(pos_tzero, pos_tzero + tangent_component*tangent(t=t0), rgbcolor=(1,0,1) ) norcomp = arrow3d(pos_tzero, pos_tzero + normal_component*normal(t=t0), rgbcolor=(1,0,1)) |
| Line 930: | Line 951: |
| print "Position vector: r(t)=", position(t) print "Speed is ", N(speed(t0)) print "Curvature is ", N(curvature) ## print "Torsion is ", N(torsion) print "Right-click on graphic to zoom to 400%" print "Drag graphic to rotate" |
print("Position vector: r(t)=", position) print("Speed is ", N(speed(t=t0))) print("Curvature is ", N(curvature)) ## print("Torsion is ", N(torsion)) print() print("Right-click on graphic to zoom to 400%") print("Drag graphic to rotate") |
| Line 947: | Line 968: |
| http://www.sagenb.org/home/pub/2828/ | http://sagenb.mc.edu/home/pub/97/ |
| Line 957: | Line 978: |
| ## An updated version of this worksheet may be available at http://sagenb.mc.edu | |
| Line 962: | Line 982: |
| var('x,y,z') Rmin=1/10 |
|
| Line 964: | Line 985: |
| @interact def _(f=input_box(default=(x^3-y^3)/(x^2+y^2)),R=slider(0.1/10,Rmax,1/10,2),x0=(0),y0=(0)): |
@interact(layout=dict(top=[['f'],['x0'],['y0']], bottom=[['in_3d','curves','R','graphjmol']])) def _(f=input_box((x^2-y^2)/(x^2+y^2),width=30,label='$f(x)$'), R=slider(Rmin,Rmax,1/10,Rmax,label=', $R$'), x0=input_box(0,width=10,label='$x_0$'), y0=input_box(0,width=10,label='$y_0$'), curves=checkbox(default=false,label='Show curves'), in_3d=checkbox(default=false,label='3D'), graphjmol=checkbox(default=true,label='Interactive graph')): if graphjmol: view_method = 'jmol' else: view_method = 'tachyon' |
| Line 973: | Line 1005: |
| Line 975: | Line 1007: |
| limit = plot3d(g,(t,0,2*pi),(r,1/100,R),transformation=cylinder,rgbcolor=(0,1,0)) | collapsing_surface = plot3d(g,(t,0,2*pi),(r,1/100,R),transformation=cylinder,rgbcolor=(0,1,0)) |
| Line 977: | Line 1009: |
| show(surface+limit) print html('Enter $(x_0 ,y_0 )$ above and see what happens as R approaches zero.') print html('The surface has a limit as $(x,y)$ approaches ('+str(x0)+','+str(y0)+') if the green region collapses to a point') |
G = surface+collapsing_surface pretty_print(html('Enter $(x_0 ,y_0 )$ above and see what happens as $ R \\rightarrow 0 $.')) pretty_print(html('The surface has a limit as $(x,y) \\rightarrow $ ('+str(x0)+','+str(y0)+') if the green region collapses to a point.')) # If checked, add a couple of curves on the surface corresponding to limit as x->x0 for y=x^(3/5), # and as y->y0 for x=y^(3/5). Should make this more robust but perhaps using # these relatively obtuse curves could eliminate problems. if curves: curve_x = parametric_plot3d([x0-t,y0-t^(3/5),f(x=x0-t,y=y0-t^(3/5))],(t,Rmin,Rmax),color='red',thickness=10) curve_y = parametric_plot3d([x0+t^(3/5),y0+t,f(x=x0+t^(3/5),y=y0+t)],(t,Rmin,Rmax),color='red',thickness=10) R2 = Rmin/4 G += arrow((x0-Rmin,y0-Rmin^(3/5),f(x=x0-Rmin,y=y0-Rmin^(3/5))),(x0-R2,y0-R2^(3/5),f(x=x0-R2,y=y0-R2^(3/5))),size=30 ) G += arrow((x0+Rmin^(3/5),y0+Rmin,f(x=x0+Rmin^(3/5),y=y0+Rmin)),(x0+R2^(3/5),y0+R2,f(x=x0+R2^(3/5),y=y0+R2)),size=30 ) limit_x = limit(f(x=x0-t,y=y0-t^(3/5)),t=0) limit_y = limit(f(x=x0+t^(3/5),y=y0+t),t=0) text_x = text3d(limit_x,(x0,y0,limit_x)) text_y = text3d(limit_y,(x0,y0,limit_y)) G += curve_x+curve_y+text_x+text_y pretty_print(html('The red curves represent a couple of trajectories on the surface. If they do not meet, then')) pretty_print(html('there is also no limit. (If computer hangs up, likely the computer can not do these limits.)')) pretty_print(html(r'<center><font color="red">$\lim_{(x,?)\rightarrow(x_0,y_0)} f(x,y) =%s$</font>'%str(limit_x)+r' and <font color="red">$\lim_{(?,y)\rightarrow(x_0,y_0)} f(x,y) =%s$</font></center>'%str(limit_y))) if in_3d: show(G,stereo="redcyan",viewer=view_method) else: show(G,perspective_depth=true,viewer=view_method) |
| Line 1001: | Line 1060: |
| Rmax=2 @interact def _(f=input_box(default=(x^3-y^3)/(x^2+y^2)), N=slider(5,100,1,10,label='Number of Contours'), x0=(0),y0=(0)): print html('Enter $(x_0 ,y_0 )$ above and see what happens as the number of contour levels increases.') print html('A surface will have a limit in the center of this graph provided there is not a sudden change in color there.') |
var('x,y,z,u') @interact(layout=dict(top=[['f'],['x0'],['y0']], bottom=[['N'],['R']])) def _(f=input_box(default=(x*y^2)/(x^2+y^4),width=30,label='$f(x)$'), N=slider(5,100,1,10,label='Number of Contours'), R=slider(0.1,1,0.01,1,label='Radius of circular neighborhood'), x0=input_box(0,width=10,label='$x_0$'), y0=input_box(0,width=10,label='$y_0$')): pretty_print(html(r'Enter $(x_0 ,y_0 )$ above and see what happens as the number of contour levels $\rightarrow \infty $.')) pretty_print(html('A surface will have a limit in the center of this graph provided there is not a sudden change in color there.')) # Need to make certain the min and max contour lines are not huge due to asymptotes. If so, clip and start contours at some reasonable # values so that there are a nice collection of contours to show around the desired point. |
| Line 1011: | Line 1076: |
| surface += parametric_plot([R*cos(u),R*sin(u)],[0,2*pi],color='black') # Nice to use if f=x*y^2/(x^2 + y^4) # var('u') # surface += parametric_plot([u^2,u],[u,-1,1],color='black') |
|
| Line 1012: | Line 1081: |
| show(limit_point+surface)}}} | # show(limit_point+surface) show(surface) }}} |
| Line 1089: | Line 1160: |
| html(r'Function $ f(x,y)=%s$ '%latex(f(x,y))) | pretty_print(html(r'Function $ f(x,y)=%s$ '%latex(f(x,y)))) |
| Line 1103: | Line 1174: |
| html(r'<tr><td>$\quad f(%s,%s)\quad $</td><td>$\quad %s$</td>\ </tr>'%(latex(x0),latex(y0),z0.n())) |
pretty_print(html(r'<tr><td>$\quad f(%s,%s)\quad $</td><td>$\quad %s$</td>\ </tr>'%(latex(x0),latex(y0),z0.n()))) |
| Line 1137: | Line 1208: |
| html('Points x0 and y0 are values where the exact value of the function \ | pretty_print(html('Points x0 and y0 are values where the exact value of the function \ |
| Line 1139: | Line 1210: |
| and approximation by differential at shifted point are compared.') | and approximation by differential at shifted point are compared.')) |
| Line 1157: | Line 1228: |
| html(r'Function $ f(x,y)=%s \approx %s $ '%(latex(f(x,y)),latex(tangent(x,y)))) html(r' $f %s = %s$'%(latex((x0,y0)),latex(exact_value_ori))) html(r'Shifted point $%s$'%latex(((x0+deltax),(y0+deltay)))) html(r'Value of the function in shifted point is $%s$'%f(x0+deltax,y0+deltay)) html(r'Value on the tangent plane in shifted point is $%s$'%latex(approx_value)) html(r'Error is $%s$'%latex(abs_error)) |
pretty_print(html(r'Function $ f(x,y)=%s \approx %s $ '%(latex(f(x,y)),latex(tangent(x,y))))) pretty_print(html(r' $f %s = %s$'%(latex((x0,y0)),latex(exact_value_ori)))) pretty_print(html(r'Shifted point $%s$'%latex(((x0+deltax),(y0+deltay))))) pretty_print(html(r'Value of the function in shifted point is $%s$'%f(x0+deltax,y0+deltay))) pretty_print(html(r'Value on the tangent plane in shifted point is $%s$'%latex(approx_value))) pretty_print(html(r'Error is $%s$'%latex(abs_error))) |
| Line 1180: | Line 1251: |
| order=(1..10)): | order=[1..10]): |
| Line 1199: | Line 1270: |
| html('$F(x,y) = e^{-(x^2+y^2)/2} \\cos(y) \\sin(x^2+y^2)$') | pretty_print(html('$F(x,y) = e^{-(x^2+y^2)/2} \\cos(y) \\sin(x^2+y^2)$')) |
| Line 1209: | Line 1280: |
| http://www.sagenb.org/home/pub/2829/ | https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2829.sagews |
| Line 1316: | Line 1387: |
| http://www.sagenb.org/home/pub/2826/ | http://sagenb.mc.edu/home/pub/89/ Note that this works in Sage cell, but causes a zip file error in Jupyter |
| Line 1323: | Line 1396: |
| ## | |
| Line 1325: | Line 1399: |
| @interact def _(f=input_box(default=6-4*x^2-y^2*2/5,label='$f(x,y) = $'), g=input_box(default=-2+sin(x)+sin(y),label='$g(x,y) = $'), u=input_box(default=cos(t),label='$u(t) = $'), v=input_box(default=2*sin(t),label='$v(t) = $'), a=input_box(default=0,label='$a = $'), b=input_box(default=3*pi/2,label='$b = $'), |
@interact(layout=dict(top=[['f','u'],['g','v']], left=[['a'],['b'],['in_3d'],['smoother']], bottom=[['xx','yy']])) def _(f=input_box(default=6-4*x^2-y^2*2/5,label='Top = $f(x,y) = $',width=30), g=input_box(default=-2+sin(x)+sin(y),label='Bottom = $g(x,y) = $',width=30), u=input_box(default=cos(t),label=' $ x = u(t) = $',width=20), v=input_box(default=2*sin(t),label=' $ y = v(t) = $',width=20), a=input_box(default=0,label='$a = $',width=10), b=input_box(default=3*pi/2,label='$b = $',width=10), |
| Line 1334: | Line 1410: |
| smoother=checkbox(default=false)): | in_3d = checkbox(default=true,label='3D'), smoother=checkbox(default=false), auto_update=true): |
| Line 1336: | Line 1414: |
| ds = sqrt(derivative(u(t),t)^2+derivative(v(t),t)^2) | ds = sqrt(derivative(u,t)^2+derivative(v,t)^2) |
| Line 1340: | Line 1418: |
| A = (f(x=u(t),y=v(t))-g(x=u(t),y=v(t)))*ds.simplify_trig().simplify() | A = (f(x=u,y=v)-g(x=u,y=v))*ds.simplify_trig().simplify() |
| Line 1345: | Line 1423: |
| line_integral = integral(A,t,a,b) | # If you want Sage to try, uncomment the lines below. # line_integral = integrate(A,t,a,b) # html(r'<align=center size=+1>Lateral Surface Area = $ %s $ </font>'%latex(line_integral)) |
| Line 1347: | Line 1429: |
| html(r'<h4 align=center>Lateral Surface Area = $ %s $ </h4>'%latex(line_integral)) html(r'<h4 align=center>Lateral Surface $ \approx $ %s</h2>'%str(line_integral_approx)) |
pretty_print(html(r'<font align=center size=+1>Lateral Surface $ \approx $ %s</font>'%str(line_integral_approx))) |
| Line 1357: | Line 1437: |
| G += parametric_plot3d([u,v,g(x=u(t),y=v(t))],(t,a,b),thickness=2,color='red') G += parametric_plot3d([u,v,f(x=u(t),y=v(t))],(t,a,b),thickness=2,color='red') |
G += parametric_plot3d([u,v,g(x=u,y=v)],(t,a,b),thickness=2,color='red') G += parametric_plot3d([u,v,f(x=u,y=v)],(t,a,b),thickness=2,color='red') |
| Line 1367: | Line 1447: |
| G += parametric_plot3d([u(w),v(w),s*f(x=u(w),y=v(w))+(1-s)*g(x=u(w),y=v(w))],(s,0,1),thickness=lat_thick,color='yellow',opacity=0.9) show(G,spin=true) |
G += parametric_plot3d([u(t=w),v(t=w),s*f(x=u(t=w),y=v(t=w))+(1-s)*g(x=u(t=w),y=v(t=w))],(s,0,1),thickness=lat_thick,color='yellow',opacity=0.9) if in_3d: show(G,stereo='redcyan',spin=true) else: show(G,perspective_depth=true,spin=true) |
| Line 1375: | Line 1459: |
Note that this works in Sage cell, but causes a zip file error in Jupyter. |
|
| Line 1394: | Line 1480: |
| http://www.sagenb.org/home/pub/2827/ | https://cloud.sagemath.com/projects/19575ea0-317e-402b-be57-368d04c113db/files/pub/2801-2901/2827-$%20%5Cint_%7BC%7D%20%5Cleft%20%5Clangle%20M,N,P%20%5Cright%20%5Crangle%20dr%20$%20=%20$%20%25s%20$.sagews |
| Line 1423: | Line 1509: |
| u(t) = u v(t) = v w(t) = w |
|
| Line 1430: | Line 1519: |
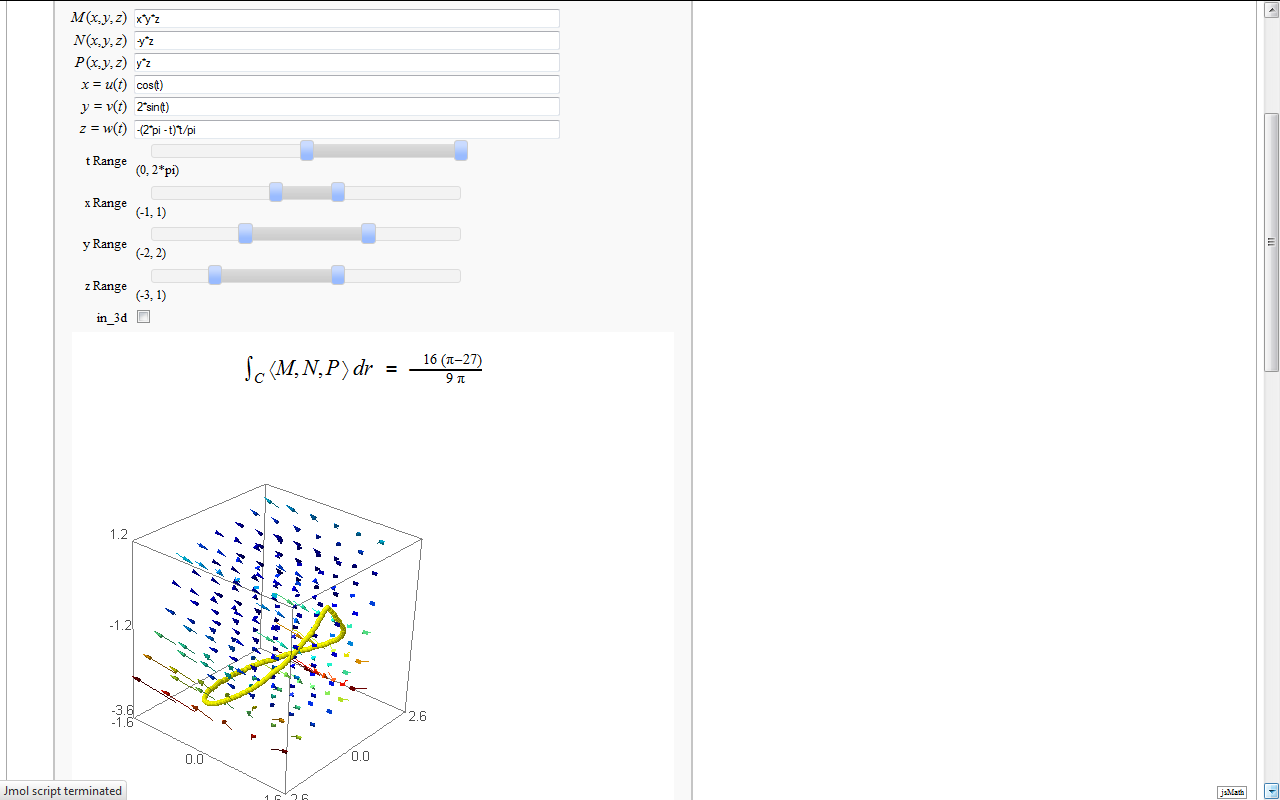
| html(r'<h2 align=center>$ \int_{C} \left \langle M,N,P \right \rangle dr $ = $ %s $ </h2>'%latex(line_integral)) | pretty_print(html(r'<h2 align=center>$ \int_{C} \left \langle M,N,P \right \rangle dr $ = $ %s $ </h2>'%latex(line_integral))) |
Sage Interactions - Calculus
goto interact main page
Contents
-
Sage Interactions - Calculus
- Root Finding Using Bisection
- Newton's Method
- A contour map and 3d plot of two inverse distance functions
- A simple tangent line grapher
- Numerical integrals with the midpoint rule
- Numerical integrals with various rules
- Some polar parametric curves
- Function tool
- Newton-Raphson Root Finding
- Coordinate Transformations
- Taylor Series
- Illustration of the precise definition of a limit
- A graphical illustration of sin(x)/x -> 1 as x-> 0
- Quadric Surface Plotter
- The midpoint rule for numerically integrating a function of two variables
- Gaussian (Legendre) quadrature
- Vector Calculus, 2-D Motion
- Vector Calculus, 3-D Motion
- Multivariate Limits by Definition
- Directional Derivatives
- 3D graph with points and curves
- Approximating function in two variables by differential
- Taylor approximations in two variables
- Volumes over non-rectangular domains
- Lateral Surface Area
- Parametric surface example
- Line Integrals in 3D Vector Field
Root Finding Using Bisection
by William Stein
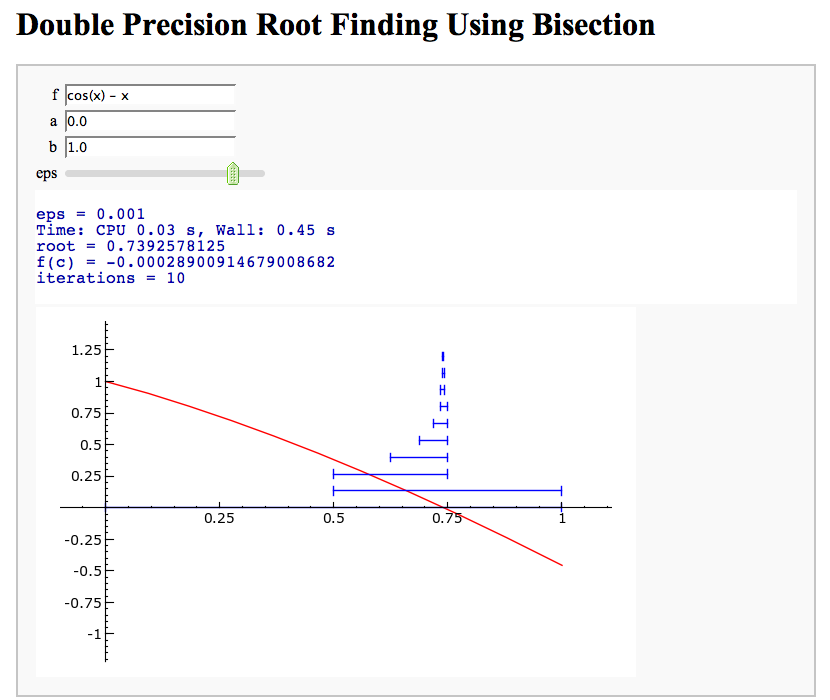
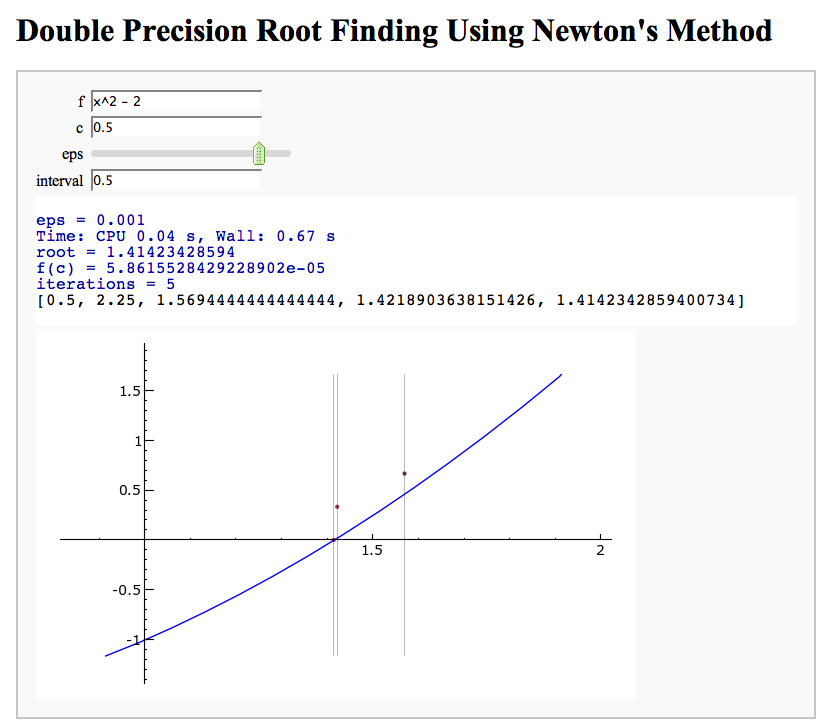
Newton's Method
Note that there is a more complicated Newton's method below.
by William Stein
A contour map and 3d plot of two inverse distance functions
by William Stein
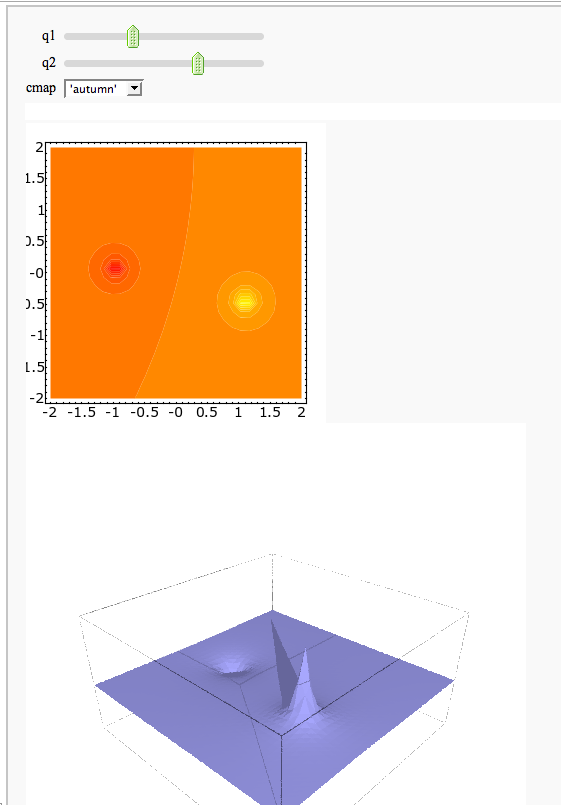
A simple tangent line grapher
by Marshall Hampton
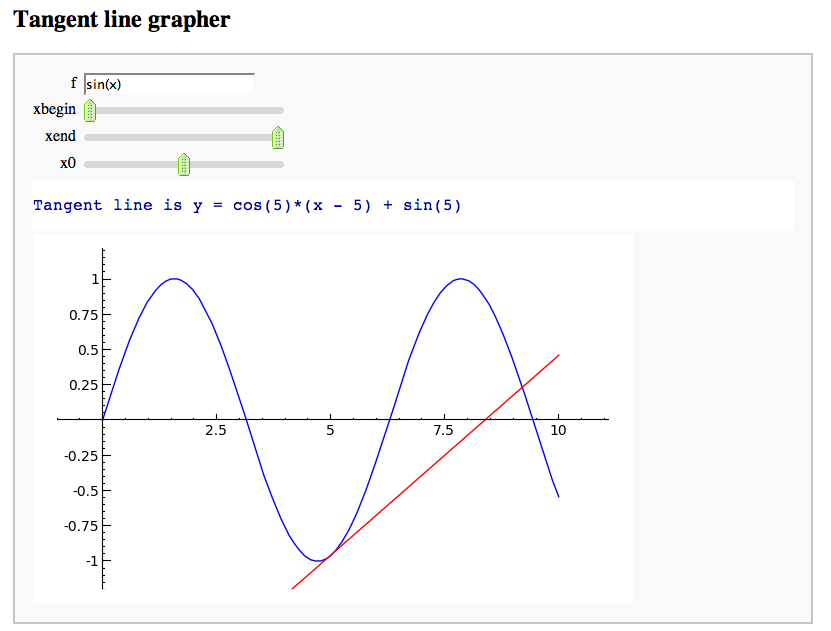
Numerical integrals with the midpoint rule
by Marshall Hampton
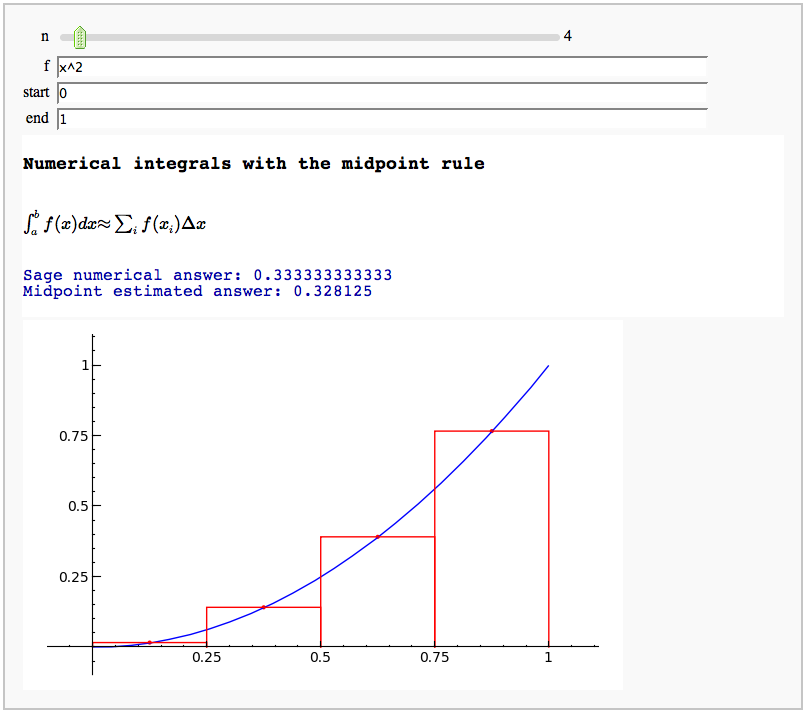
Numerical integrals with various rules
by Nick Alexander (based on the work of Marshall Hampton)
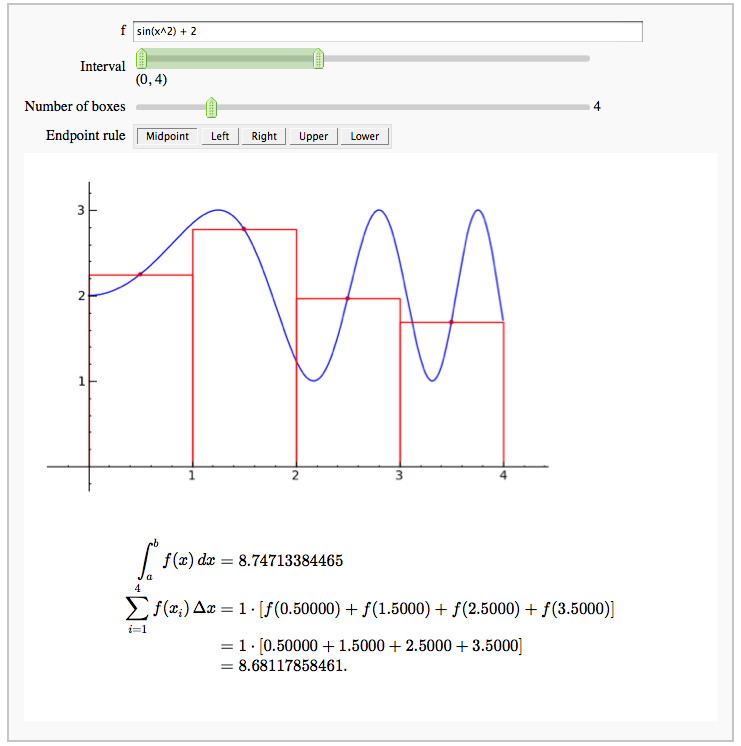
Some polar parametric curves
by Marshall Hampton. This is not very general, but could be modified to show other families of polar curves.
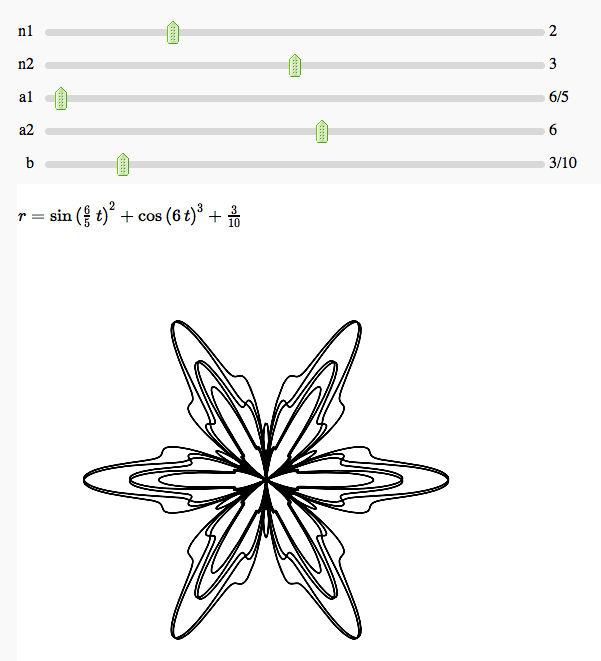
Function tool
Enter symbolic functions f, g, and a, a range, then click the appropriate button to compute and plot some combination of f, g, and a along with f and g. This is inspired by the Matlab funtool GUI.
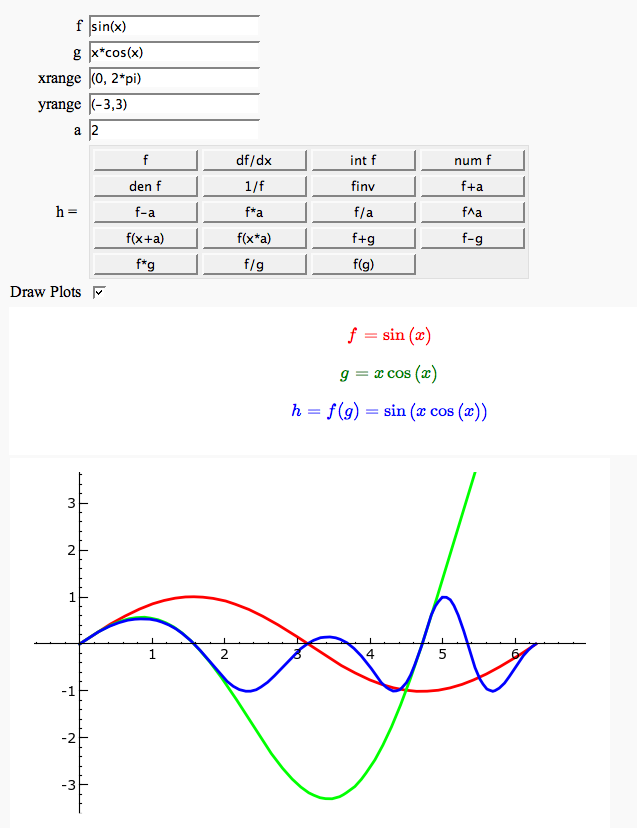
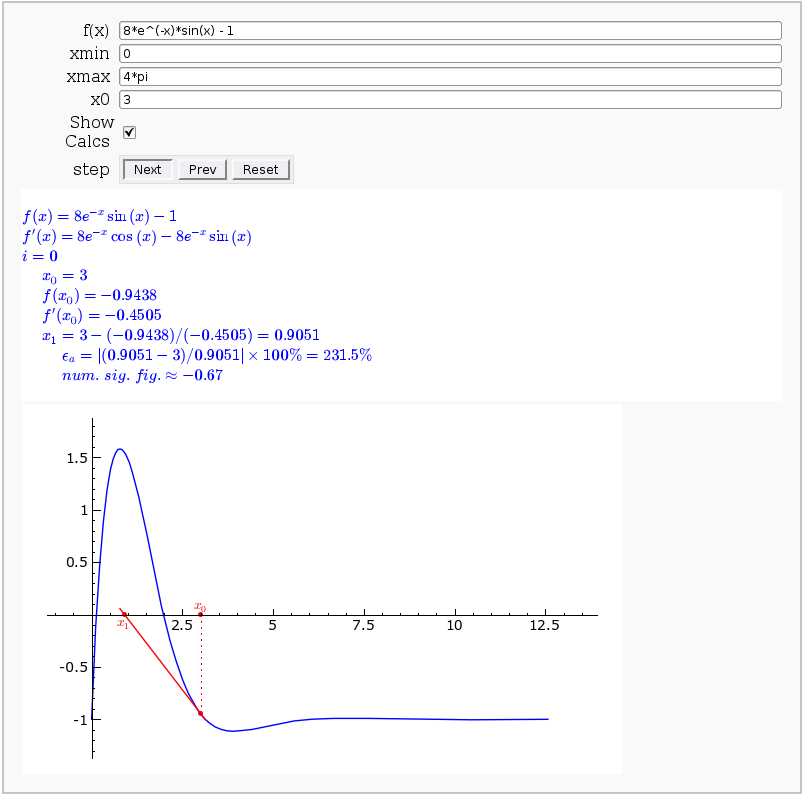
Newton-Raphson Root Finding
by Neal Holtz
This allows user to display the Newton-Raphson procedure one step at a time. It uses the heuristic that, if any of the values of the controls change, then the procedure should be re-started, else it should be continued.
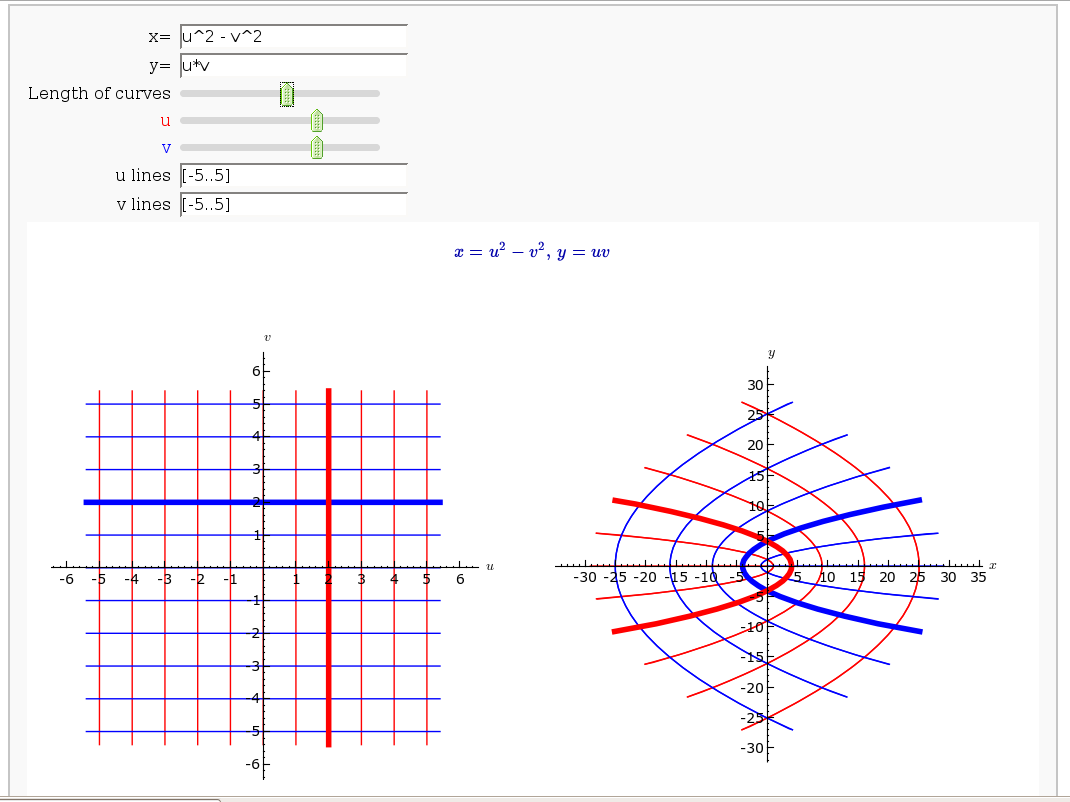
Coordinate Transformations
by Jason Grout
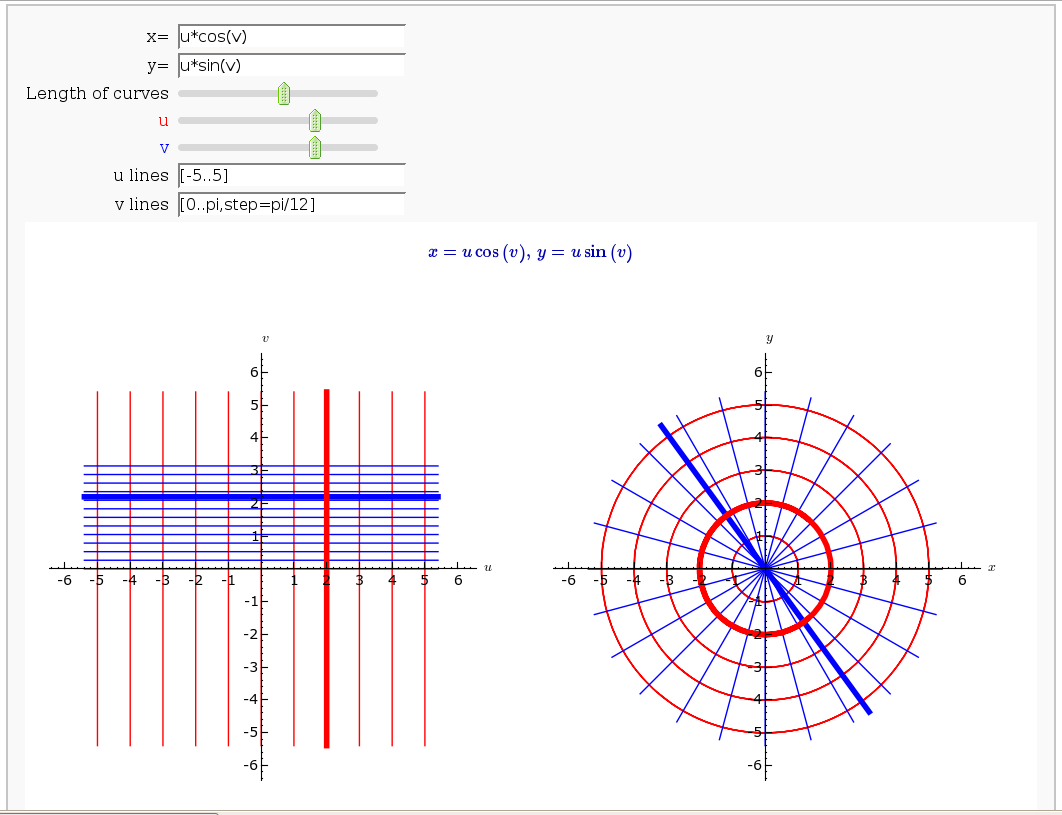
Taylor Series
by Harald Schilly
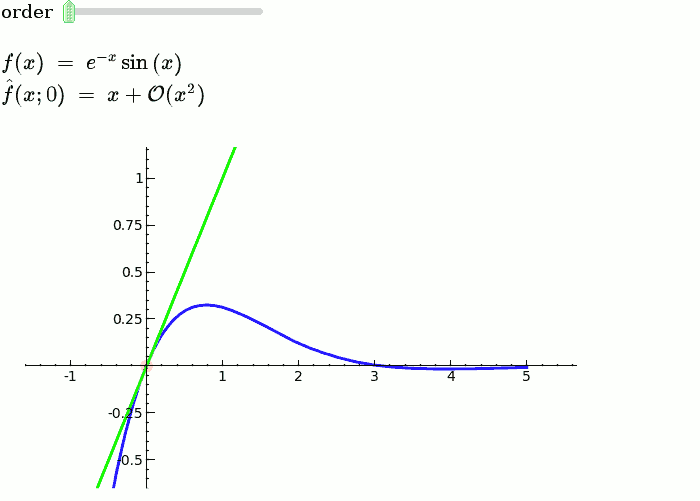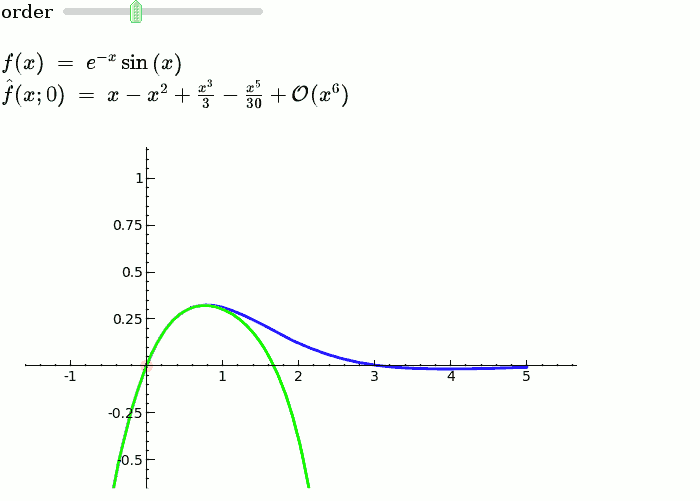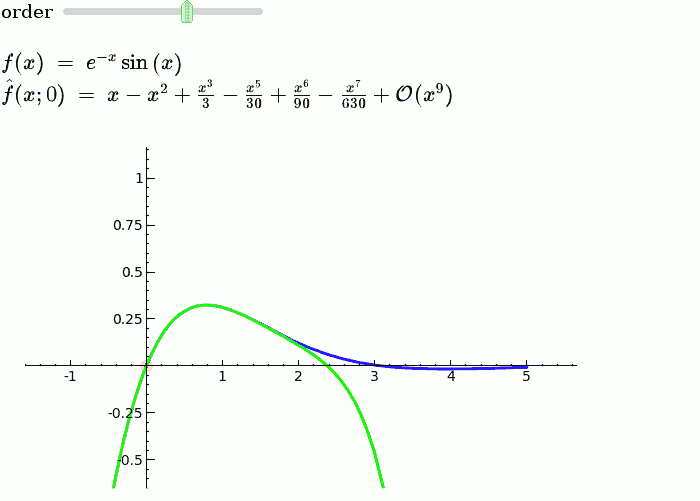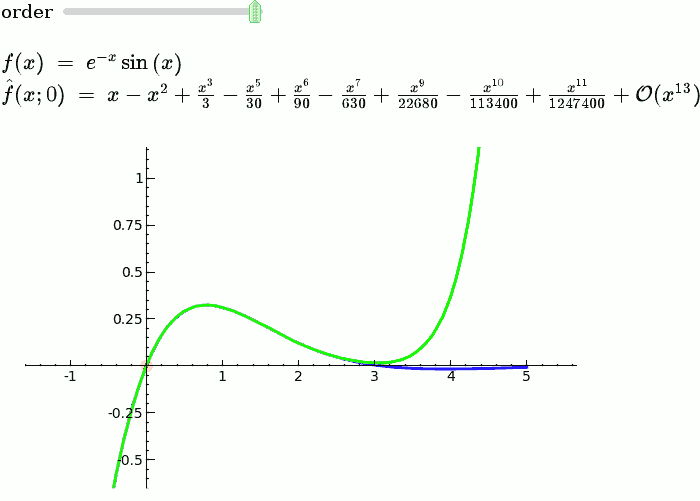
Illustration of the precise definition of a limit
by John Perry
I'll break tradition and put the image first. Apologies if this is Not A Good Thing.
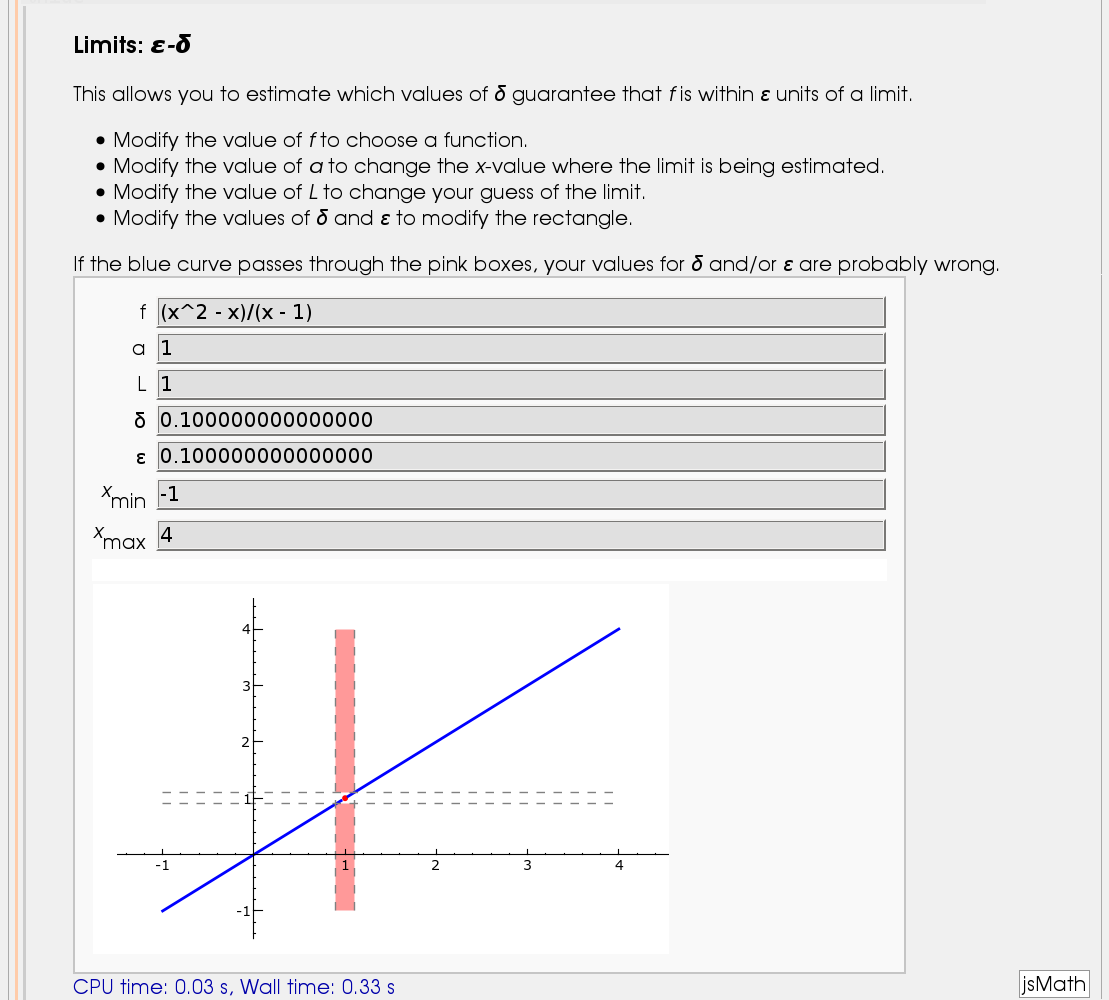
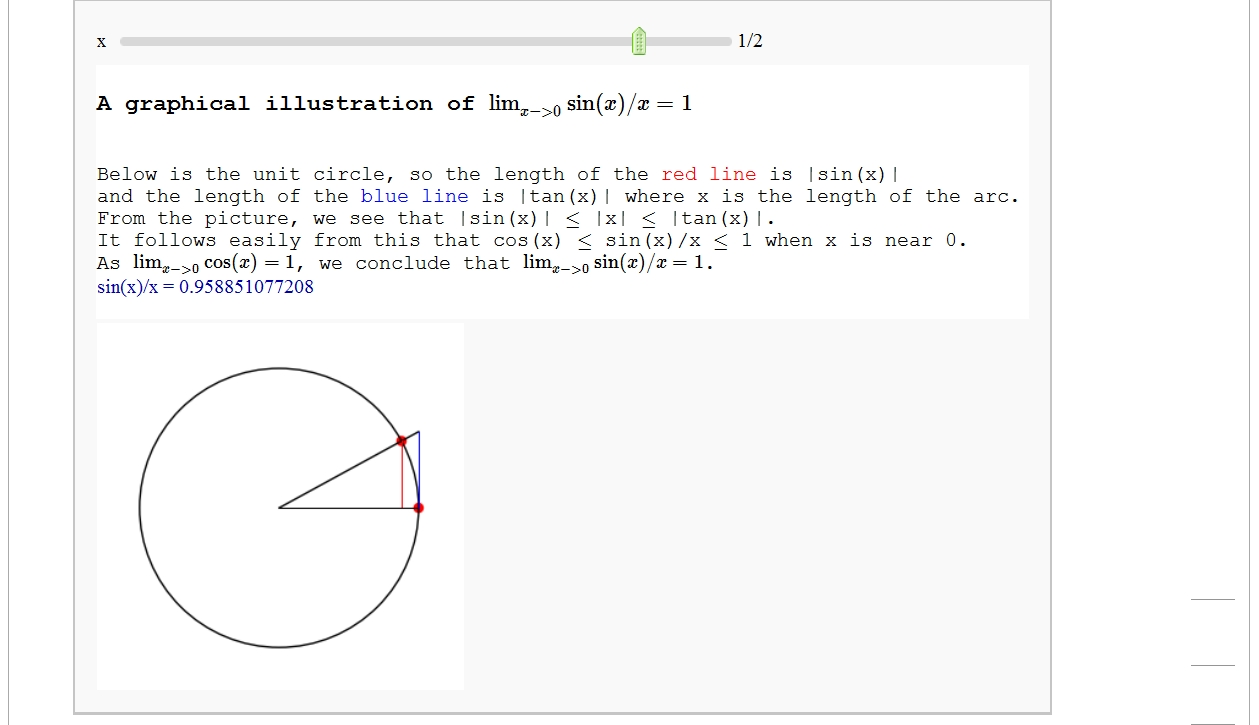
A graphical illustration of sin(x)/x -> 1 as x-> 0
by Wai Yan Pong
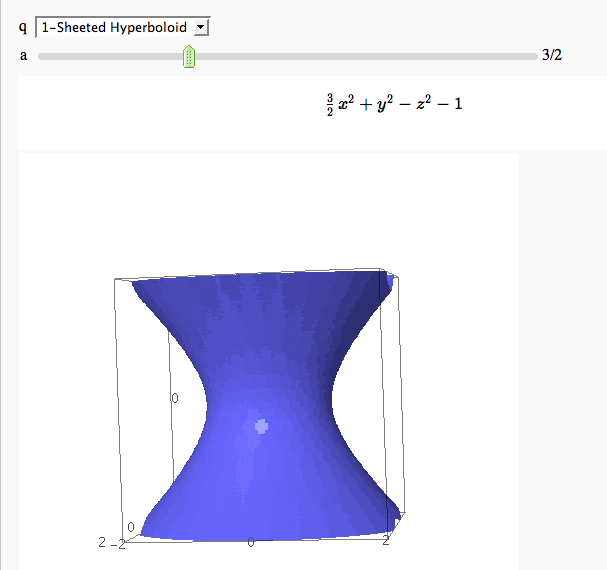
Quadric Surface Plotter
by Marshall Hampton. This is pretty simple, so I encourage people to spruce it up. In particular, it isn't set up to show all possible types of quadrics.
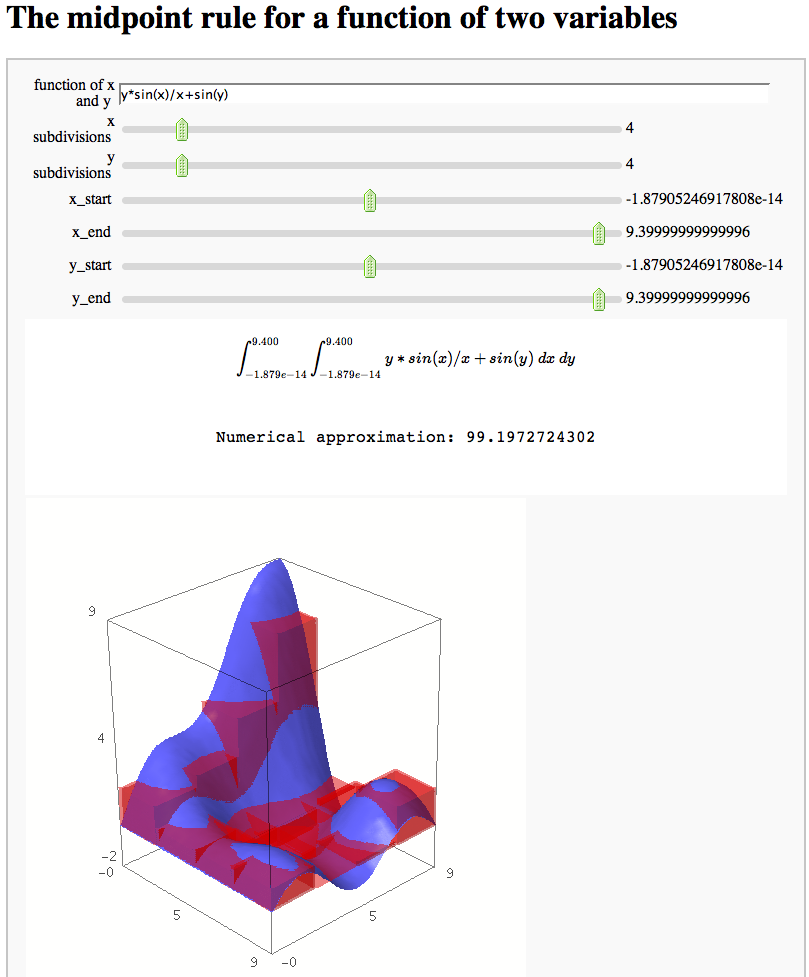
The midpoint rule for numerically integrating a function of two variables
by Marshall Hampton
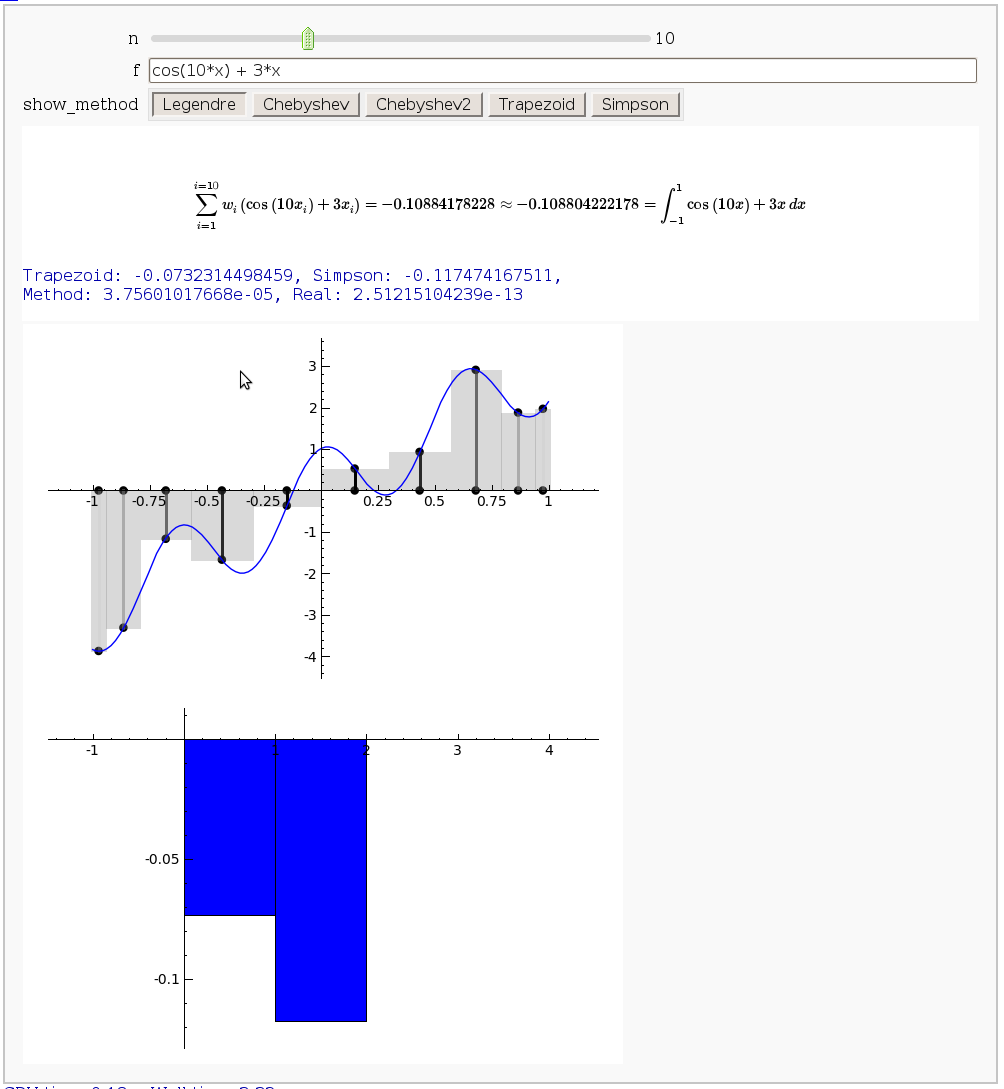
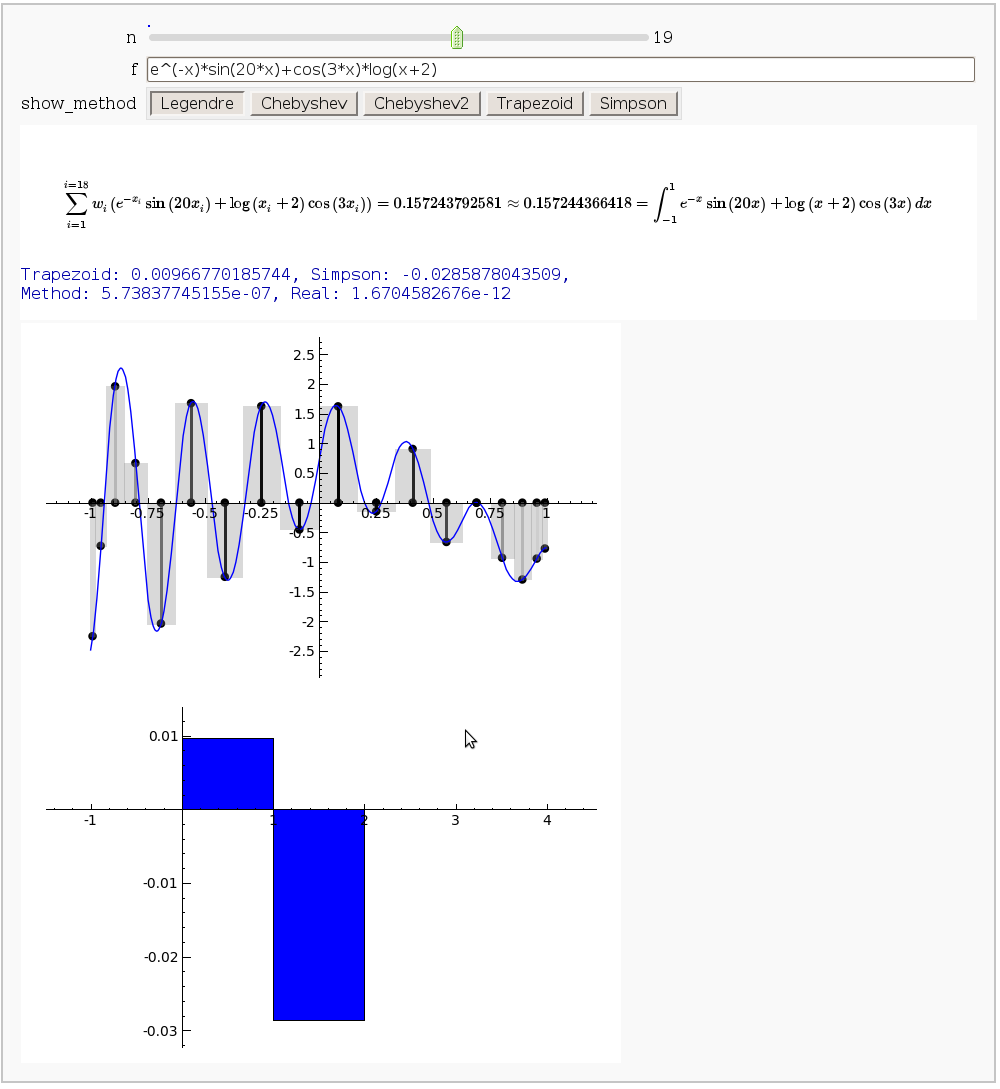
Gaussian (Legendre) quadrature
by Jason Grout
The output shows the points evaluated using Gaussian quadrature (using a weight of 1, so using Legendre polynomials). The vertical bars are shaded to represent the relative weights of the points (darker = more weight). The error in the trapezoid, Simpson, and quadrature methods is both printed out and compared through a bar graph. The "Real" error is the error returned from scipy on the definite integral.
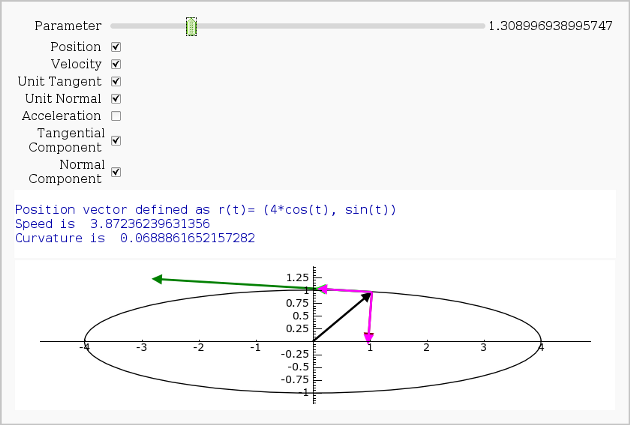
Vector Calculus, 2-D Motion
By Rob Beezer
A fast_float() version is available in a worksheet
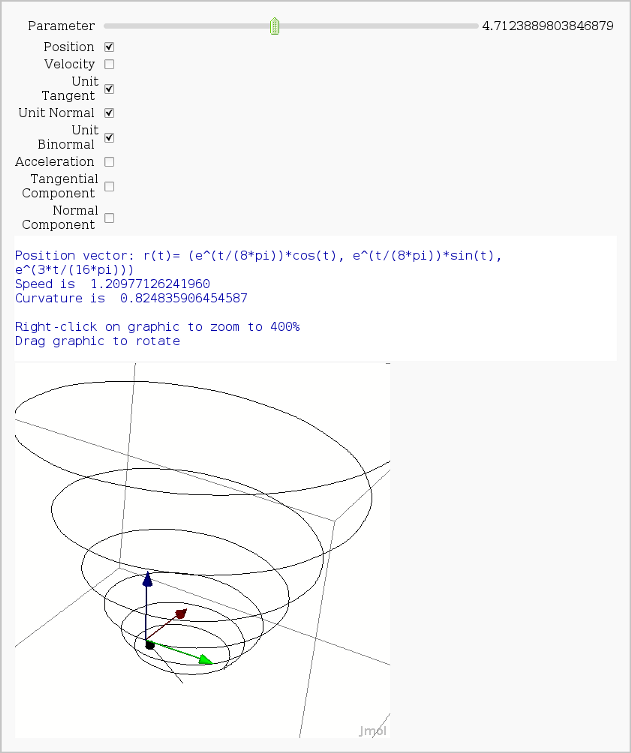
Vector Calculus, 3-D Motion
by Rob Beezer
Available as a worksheet
Multivariate Limits by Definition
by John Travis
http://sagenb.mc.edu/home/pub/97/
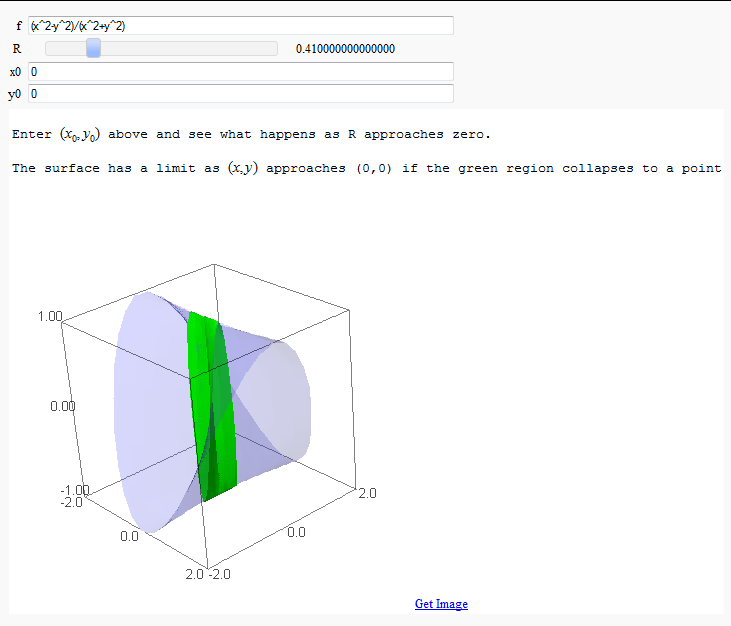
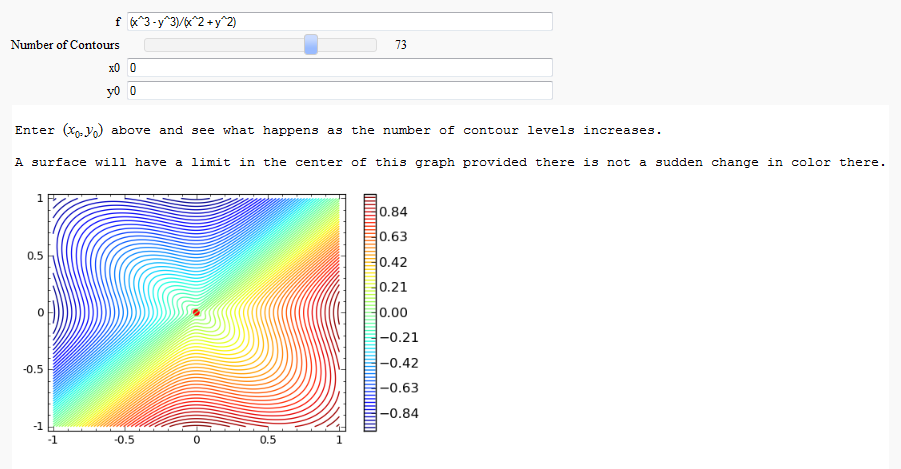
Directional Derivatives
This interact displays graphically a tangent line to a function, illustrating a directional derivative (the slope of the tangent line).
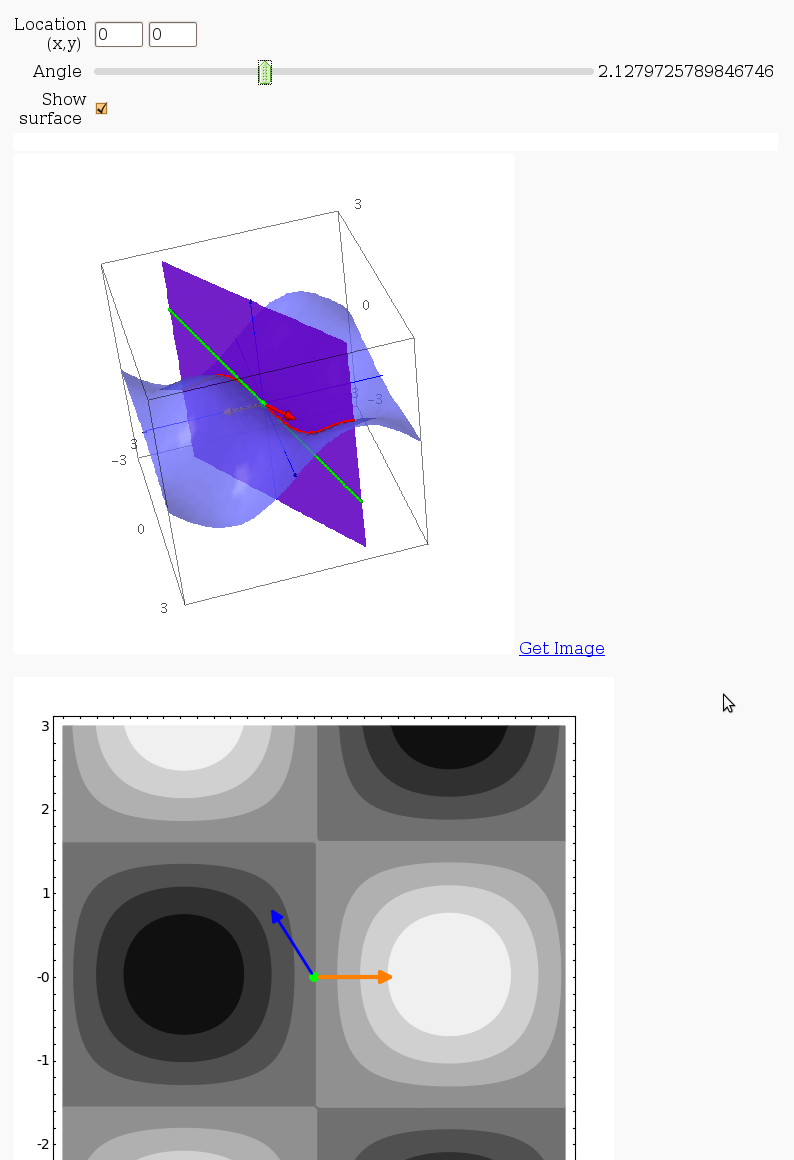
3D graph with points and curves
By Robert Marik
This sagelet is handy when showing local, constrained and absolute maxima and minima in two variables. Available as a worksheet
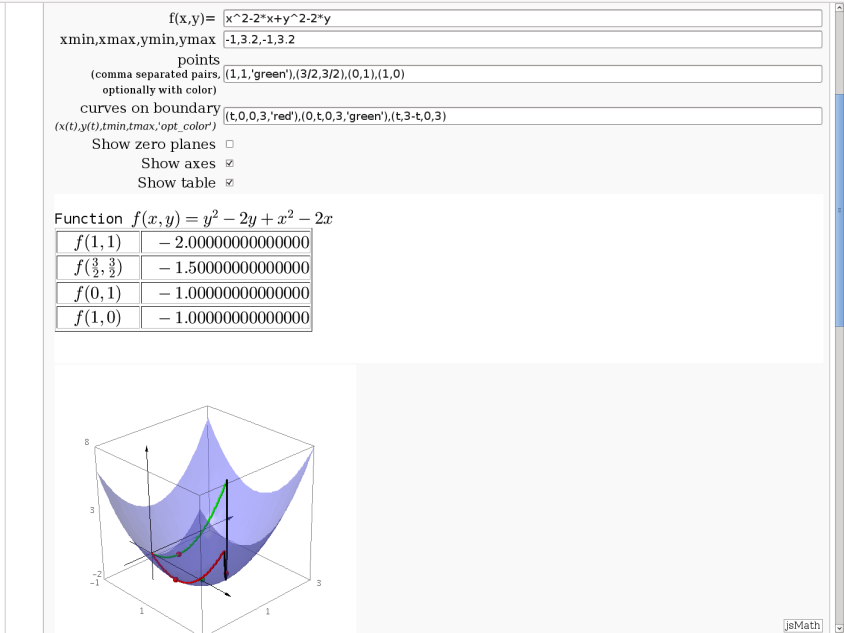
Approximating function in two variables by differential
by Robert Marik
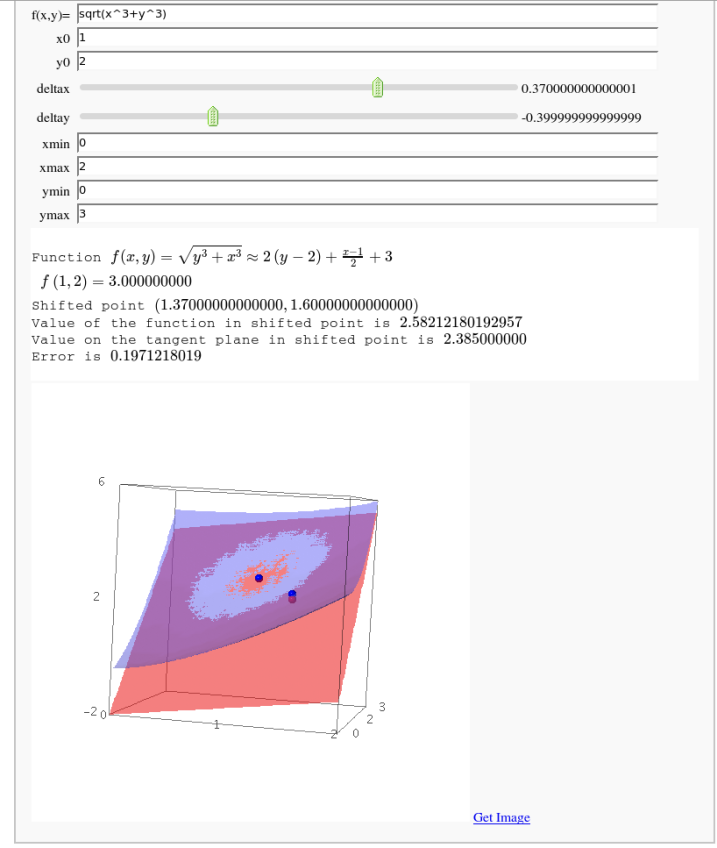
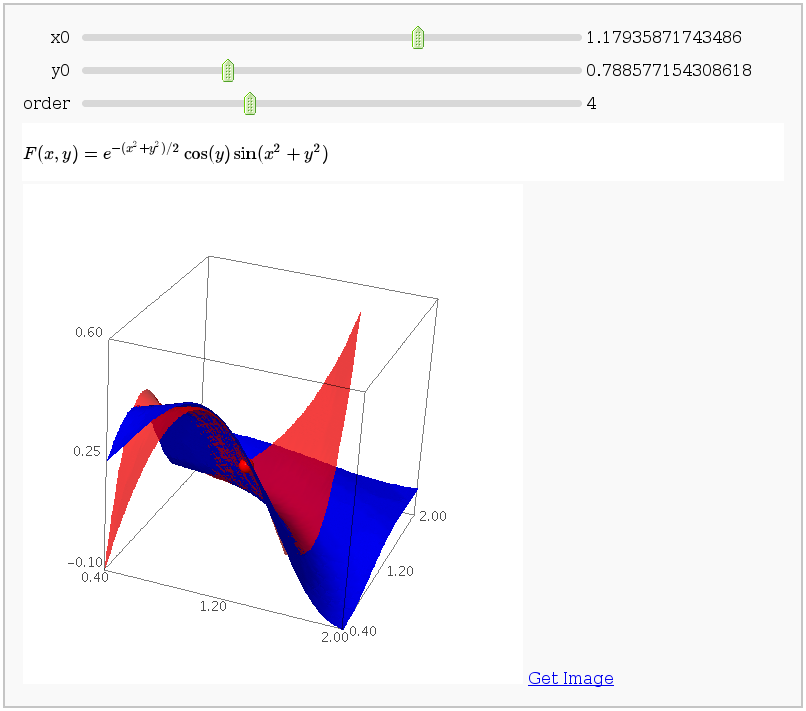
Taylor approximations in two variables
by John Palmieri
This displays the nth order Taylor approximation, for n from 1 to 10, of the function sin(x2 + y2) cos(y) exp(-(x2+y2)/2).
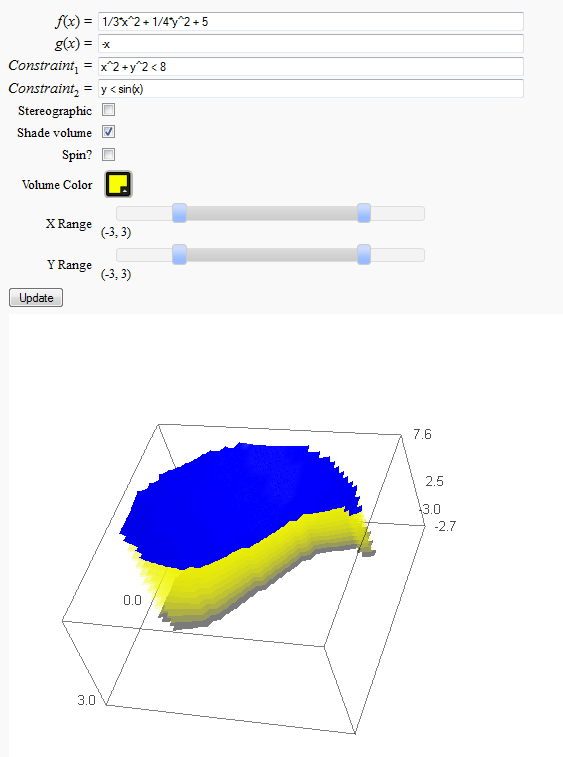
Volumes over non-rectangular domains
by John Travis
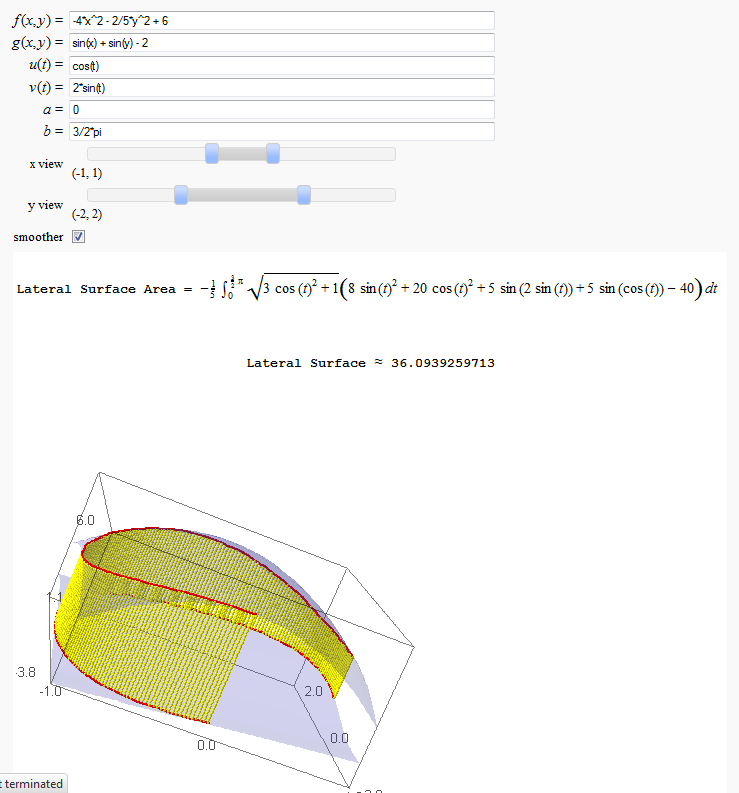
Lateral Surface Area
by John Travis
http://sagenb.mc.edu/home/pub/89/
Note that this works in Sage cell, but causes a zip file error in Jupyter
Parametric surface example
by Marshall Hampton
Note that this works in Sage cell, but causes a zip file error in Jupyter.
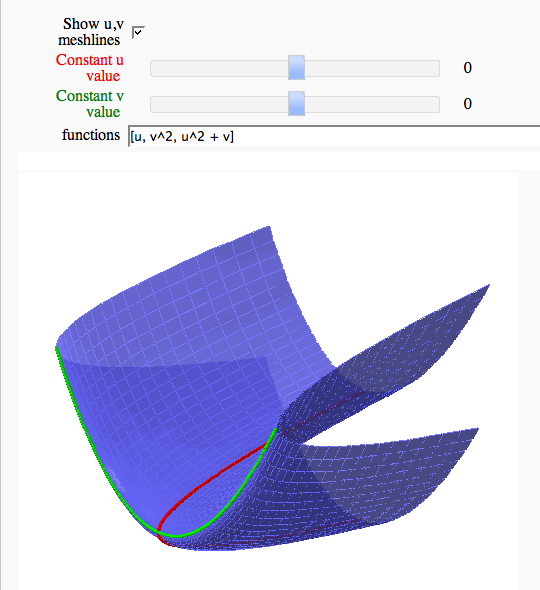
Line Integrals in 3D Vector Field
by John Travis