|
Size: 11104
Comment:
|
Size: 44752
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| goto [:interact:interact main page] |
goto [[interact|interact main page]] <<TableOfContents>> == Root Finding Using Bisection == by William Stein {{{ def bisect_method(f, a, b, eps): try: f = f._fast_float_(f.variables()[0]) except AttributeError: pass intervals = [(a,b)] two = float(2); eps = float(eps) while True: c = (a+b)/two fa = f(a); fb = f(b); fc = f(c) if abs(fc) < eps: return c, intervals if fa*fc < 0: a, b = a, c elif fc*fb < 0: a, b = c, b else: raise ValueError, "f must have a sign change in the interval (%s,%s)"%(a,b) intervals.append((a,b)) html("<h1>Double Precision Root Finding Using Bisection</h1>") @interact def _(f = cos(x) - x, a = float(0), b = float(1), eps=(-3,(-16..-1))): eps = 10^eps print "eps = %s"%float(eps) try: time c, intervals = bisect_method(f, a, b, eps) except ValueError: print "f must have opposite sign at the endpoints of the interval" show(plot(f, a, b, color='red'), xmin=a, xmax=b) else: print "root =", c print "f(c) = %r"%f(c) print "iterations =", len(intervals) P = plot(f, a, b, color='red') h = (P.ymax() - P.ymin())/ (1.5*len(intervals)) L = sum(line([(c,h*i), (d,h*i)]) for i, (c,d) in enumerate(intervals) ) L += sum(line([(c,h*i-h/4), (c,h*i+h/4)]) for i, (c,d) in enumerate(intervals) ) L += sum(line([(d,h*i-h/4), (d,h*i+h/4)]) for i, (c,d) in enumerate(intervals) ) show(P + L, xmin=a, xmax=b) }}} {{attachment:bisect.png}} == Newton's Method == Note that there is a more complicated Newton's method below. by William Stein {{{ def newton_method(f, c, eps, maxiter=100): x = f.variables()[0] fprime = f.derivative(x) try: g = f._fast_float_(x) gprime = fprime._fast_float_(x) except AttributeError: g = f; gprime = fprime iterates = [c] for i in xrange(maxiter): fc = g(c) if abs(fc) < eps: return c, iterates c = c - fc/gprime(c) iterates.append(c) return c, iterates html("<h1>Double Precision Root Finding Using Newton's Method</h1>") @interact def _(f = x^2 - 2, c = float(0.5), eps=(-3,(-16..-1)), interval=float(0.5)): eps = 10^(eps) print "eps = %s"%float(eps) time z, iterates = newton_method(f, c, eps) print "root =", z print "f(c) = %r"%f(z) n = len(iterates) print "iterations =", n html(iterates) P = plot(f, z-interval, z+interval, rgbcolor='blue') h = P.ymax(); j = P.ymin() L = sum(point((w,(n-1-float(i))/n*h), rgbcolor=(float(i)/n,0.2,0.3), pointsize=10) + \ line([(w,h),(w,j)],rgbcolor='black',thickness=0.2) for i,w in enumerate(iterates)) show(P + L, xmin=z-interval, xmax=z+interval) }}} {{attachment:newton.png}} |
| Line 7: | Line 93: |
| {{{ @interact def _(q1=(-1,(-3,3)), q2=(-2,(-3,3)), cmap=['autumn', 'bone', 'cool', 'copper', 'gray', 'hot', 'hsv', |
{{{ @interact def _(q1=(-1,(-3,3)), q2=(-2,(-3,3)), cmap=['autumn', 'bone', 'cool', 'copper', 'gray', 'hot', 'hsv', |
| Line 16: | Line 103: |
| show(plot3d(f, (x,-2,2), (y,-2,2)), figsize=5, viewer='tachyon') }}} attachment:mountains.png |
show(plot3d(f, (x,-2,2), (y,-2,2)), figsize=5, viewer='tachyon') }}} {{attachment:mountains.png}} |
| Line 22: | Line 109: |
| Line 38: | Line 126: |
| attachment:tangents.png | {{attachment:tangents.png}} == Numerical integrals with the midpoint rule == by Marshall Hampton {{{ var('x') @interact def midpoint(n = slider(1,100,1,4), f = input_box(default = "x^2", type = str), start = input_box(default = "0", type = str), end = input_box(default = "1", type = str)): a = N(start) b = N(end) func = sage_eval(f, locals={'x':x}) dx = (b-a)/n midxs = [q*dx+dx/2 + a for q in range(n)] midys = [func(x_val) for x_val in midxs] rects = Graphics() for q in range(n): xm = midxs[q] ym = midys[q] rects = rects + line([[xm-dx/2,0],[xm-dx/2,ym],[xm+dx/2,ym],[xm+dx/2,0]], rgbcolor = (1,0,0)) + point((xm,ym), rgbcolor = (1,0,0)) min_y = find_minimum_on_interval(func,a,b)[0] max_y = find_maximum_on_interval(func,a,b)[0] html('<h3>Numerical integrals with the midpoint rule</h3>') html('$\int_{a}^{b}{f(x) dx} {\\approx} \sum_i{f(x_i) \Delta x}$') print "\n\nSage numerical answer: " + str(integral_numerical(func,a,b,max_points = 200)[0]) print "Midpoint estimated answer: " + str(RDF(dx*sum([midys[q] for q in range(n)]))) show(plot(func,a,b) + rects, xmin = a, xmax = b, ymin = min_y, ymax = max_y) }}} {{attachment:num_int.png}} == Numerical integrals with various rules == by Nick Alexander (based on the work of Marshall Hampton) {{{ # by Nick Alexander (based on the work of Marshall Hampton) var('x') @interact def midpoint(f = input_box(default = sin(x^2) + 2, type = SR), interval=range_slider(0, 10, 1, default=(0, 4), label="Interval"), number_of_subdivisions = slider(1, 20, 1, default=4, label="Number of boxes"), endpoint_rule = selector(['Midpoint', 'Left', 'Right', 'Upper', 'Lower'], nrows=1, label="Endpoint rule")): a, b = map(QQ, interval) t = sage.calculus.calculus.var('t') func = fast_callable(f(x=t), RDF, vars=[t]) dx = ZZ(b-a)/ZZ(number_of_subdivisions) xs = [] ys = [] for q in range(number_of_subdivisions): if endpoint_rule == 'Left': xs.append(q*dx + a) elif endpoint_rule == 'Midpoint': xs.append(q*dx + a + dx/2) elif endpoint_rule == 'Right': xs.append(q*dx + a + dx) elif endpoint_rule == 'Upper': x = find_maximum_on_interval(func, q*dx + a, q*dx + dx + a)[1] xs.append(x) elif endpoint_rule == 'Lower': x = find_minimum_on_interval(func, q*dx + a, q*dx + dx + a)[1] xs.append(x) ys = [ func(x) for x in xs ] rects = Graphics() for q in range(number_of_subdivisions): xm = q*dx + dx/2 + a x = xs[q] y = ys[q] rects += line([[xm-dx/2,0],[xm-dx/2,y],[xm+dx/2,y],[xm+dx/2,0]], rgbcolor = (1,0,0)) rects += point((x, y), rgbcolor = (1,0,0)) min_y = min(0, find_minimum_on_interval(func,a,b)[0]) max_y = max(0, find_maximum_on_interval(func,a,b)[0]) # html('<h3>Numerical integrals with the midpoint rule</h3>') show(plot(func,a,b) + rects, xmin = a, xmax = b, ymin = min_y, ymax = max_y) def cap(x): # print only a few digits of precision if x < 1e-4: return 0 return RealField(20)(x) sum_html = "%s \cdot \\left[ %s \\right]" % (dx, ' + '.join([ "f(%s)" % cap(i) for i in xs ])) num_html = "%s \cdot \\left[ %s \\right]" % (dx, ' + '.join([ str(cap(i)) for i in ys ])) numerical_answer = integral_numerical(func,a,b,max_points = 200)[0] estimated_answer = dx * sum([ ys[q] for q in range(number_of_subdivisions)]) html(r''' <div class="math"> \begin{align*} \int_{a}^{b} {f(x) \, dx} & = %s \\\ \sum_{i=1}^{%s} {f(x_i) \, \Delta x} & = %s \\\ & = %s \\\ & = %s . \end{align*} </div> ''' % (numerical_answer, number_of_subdivisions, sum_html, num_html, estimated_answer)) }}} {{attachment:num_int2.png}} == Some polar parametric curves == by Marshall Hampton. This is not very general, but could be modified to show other families of polar curves. {{{ @interact def para(n1 = slider(1,5,1,default = 2), n2 = slider(1,5,1,default = 3), a1 = slider(1,10,1/10,6/5), a2 = slider(1,10,1/10,6), b = slider(0,2,1/50,0)): var('t') html('$r=' + latex(b+sin(a1*t)^n1 + cos(a2*t)^n2)+'$') p = parametric_plot((cos(t)*(b+sin(a1*t)^n1 + cos(a2*t)^n2), sin(t)*(b+sin(a1*t)^n1 + cos(a2*t)^n2)), (t,0, 20*pi), plot_points = 1024, rgbcolor = (0,0,0)) show(p, figsize = [5,5], xmin = -2-b, xmax = 2+b, ymin = -2-b, ymax = 2+b, axes = False) }}} {{attachment:polarcurves1.png}} |
| Line 41: | Line 242: |
| Enter symbolic functions $f$, $g$, and $a$, a range, then click the appropriate button to compute and plot some combination of $f$, $g$, and $a$ along with $f$ and $g$. This is inspired by the Matlab funtool GUI. |
Enter symbolic functions $f$, $g$, and $a$, a range, then click the appropriate button to compute and plot some combination of $f$, $g$, and $a$ along with $f$ and $g$. This is inspired by the Matlab funtool GUI. |
| Line 47: | Line 246: |
| Line 51: | Line 249: |
| 'f+a', 'f-a', 'f*a', 'f/a', 'f^a', 'f(x+a)', 'f(x*a)', 'f+g', 'f-g', 'f*g', 'f/g', 'f(g)'], |
'f+a', 'f-a', 'f*a', 'f/a', 'f^a', 'f(x+a)', 'f(x*a)', 'f+g', 'f-g', 'f*g', 'f/g', 'f(g)'], |
| Line 55: | Line 253: |
| Line 61: | Line 258: |
| return | return |
| Line 125: | Line 322: |
| Line 140: | Line 335: |
attachment:funtool.png |
{{attachment:funtool.png}} |
| Line 144: | Line 338: |
| Line 147: | Line 340: |
| This allows user to display the Newton-Raphson procedure one step at a time. It uses the heuristic that, if any of the values of the controls change, then the procedure should be re-started, else it should be continued. |
This allows user to display the Newton-Raphson procedure one step at a time. It uses the heuristic that, if any of the values of the controls change, then the procedure should be re-started, else it should be continued. |
| Line 155: | Line 346: |
| State = Data = None # globals to allow incremental additions to graphics | State = Data = None # globals to allow incremental changes in interaction data |
| Line 163: | Line 354: |
| step = ['Next','Reset'] ): | step = ['Next','Prev', 'Reset'] ): |
| Line 165: | Line 356: |
| prange = [xmin,xmax] | |
| Line 168: | Line 358: |
| X = [RR(x0)] # restart the plot df = diff(f) Fplot = plot(f, prange[0], prange[1]) Data = [X, df, Fplot] |
Data = [ 1 ] # reset the plot |
| Line 173: | Line 360: |
X, df, Fplot = Data i = len(X) - 1 # compute and append the next x value xi = X[i] fi = RR(f(xi)) fpi = RR(df(xi)) xip1 = xi - fi/fpi X.append(xip1) msg = xip1s = None # now check x value for reasonableness |
elif step == 'Next': N, = Data Data = [ N+1 ] elif step == 'Prev': N, = Data if N > 1: Data = [ N-1 ] N, = Data df = diff(f) theplot = plot( f, xmin, xmax ) theplot += text( '\n$x_0$', (x0,0), rgbcolor=(1,0,0), vertical_alignment="bottom" if f(x0) < 0 else "top" ) theplot += points( [(x0,0)], rgbcolor=(1,0,0) ) Trace = [] def Err( msg, Trace=Trace ): Trace.append( '<font color="red"><b>Error: %s!!</b></font>' % (msg,) ) def Disp( s, color="blue", Trace=Trace ): Trace.append( """<font color="%s">$ %s $</font>""" % (color,s,) ) Disp( """f(x) = %s""" % (latex(f),) ) Disp( """f'(x) = %s""" % (latex(df),) ) stop = False |
| Line 184: | Line 386: |
| if abs(xip1) > 10E6*(xmax-xmin): is_inf = True show_calcs = True msg = 'Derivative is 0!' xip1s = latex(xip1.sign()*infinity) X.pop() elif not ((xmin - 0.5*(xmax-xmin)) <= xip1 <= (xmax + 0.5*(xmax-xmin))): show_calcs = True msg = 'x value out of range; probable divergence!' if xip1s is None: xip1s = '%.4g' % (xip1,) def Disp( s, color="blue" ): if show_calcs: html( """<font color="%s">$ %s $</font>""" % (color,s,) ) Disp( """f(x) = %s""" % (latex(f),) + """~~~~f'(x) = %s""" % (latex(df),) ) Disp( """i = %d""" % (i,) + """~~~~x_{%d} = %.4g""" % (i,xi) + """~~~~f(x_{%d}) = %.4g""" % (i,fi) + """~~~~f'(x_{%d}) = %.4g""" % (i,fpi) ) if msg: html( """<font color="red"><b>%s</b></font>""" % (msg,) ) c = "red" else: c = "blue" Disp( r"""x_{%d} = %.4g - ({%.4g})/({%.4g}) = %s""" % (i+1,xi,fi,fpi,xip1s), color=c ) Fplot += line( [(xi,0),(xi,fi)], linestyle=':', rgbcolor=(1,0,0) ) # vert dotted line Fplot += points( [(xi,0),(xi,fi)], rgbcolor=(1,0,0) ) labi = text( '\nx%d\n' % (i,), (xi,0), rgbcolor=(1,0,0), vertical_alignment="bottom" if fi < 0 else "top" ) if is_inf: xl = xi - 0.05*(xmax-xmin) xr = xi + 0.05*(xmax-xmin) yl = yr = fi else: xl = min(xi,xip1) - 0.02*(xmax-xmin) xr = max(xi,xip1) + 0.02*(xmax-xmin) yl = -(xip1-xl)*fpi yr = (xr-xip1)*fpi Fplot += points( [(xip1,0)], rgbcolor=(0,0,1) ) # new x value labi += text( '\nx%d\n' % (i+1,), (xip1,0), rgbcolor=(1,0,0), vertical_alignment="bottom" if fi < 0 else "top" ) Fplot += line( [(xl,yl),(xr,yr)], rgbcolor=(1,0,0) ) # tangent show( Fplot+labi, xmin = prange[0], xmax = prange[1] ) Data = [X, df, Fplot] }}} attachment:newtraph.png |
xi = x0 for i in range(N): fi = RR(f(xi)) fpi = RR(df(xi)) theplot += points( [(xi,fi)], rgbcolor=(1,0,0) ) theplot += line( [(xi,0),(xi,fi)], linestyle=':', rgbcolor=(1,0,0) ) # vert dotted line Disp( """i = %d""" % (i,) ) Disp( """~~~~x_{%d} = %.4g""" % (i,xi) ) Disp( """~~~~f(x_{%d}) = %.4g""" % (i,fi) ) Disp( """~~~~f'(x_{%d}) = %.4g""" % (i,fpi) ) if fpi == 0.0: Err( 'Derivative is 0 at iteration %d' % (i+1,) ) is_inf = True show_calcs = True else: xip1 = xi - fi/fpi Disp( r"""~~~~x_{%d} = %.4g - ({%.4g})/({%.4g}) = %.4g""" % (i+1,xi,fi,fpi,xip1) ) if abs(xip1) > 10*(xmax-xmin): Err( 'Derivative is too close to 0!' ) is_inf = True show_calcs = True elif not ((xmin - 0.5*(xmax-xmin)) <= xip1 <= (xmax + 0.5*(xmax-xmin))): Err( 'x value out of range; probable divergence!' ) stop = True show_calcs = True if is_inf: xl = xi - 0.05*(xmax-xmin) xr = xi + 0.05*(xmax-xmin) yl = yr = fi else: xl = min(xi,xip1) - 0.01*(xmax-xmin) xr = max(xi,xip1) + 0.01*(xmax-xmin) yl = -(xip1-xl)*fpi yr = (xr-xip1)*fpi theplot += text( '\n$x_{%d}$' % (i+1,), (xip1,0), rgbcolor=(1,0,0), vertical_alignment="bottom" if f(xip1) < 0 else "top" ) theplot += points( [(xip1,0)], rgbcolor=(1,0,0) ) theplot += line( [(xl,yl),(xr,yr)], rgbcolor=(1,0,0) ) # tangent if stop or is_inf: break epsa = 100.0*abs((xip1-xi)/xip1) nsf = 2 - log(2.0*epsa)/log(10.0) Disp( r"""~~~~~~~~\epsilon_a = \left|(%.4g - %.4g)/%.4g\right|\times100\%% = %.4g \%%""" % (xip1,xi,xip1,epsa) ) Disp( r"""~~~~~~~~num.~sig.~fig. \approx %.2g""" % (nsf,) ) xi = xip1 show( theplot, xmin=xmin, xmax=xmax ) if show_calcs: for t in Trace: html( t ) }}} {{attachment:newtraph.png}} |
| Line 241: | Line 447: |
| {{{ | {{{ |
| Line 244: | Line 455: |
| @interact def trans(x=input_box(u^2-v^2, label="x=",type=SR), \ y=input_box(u*v, label="y=",type=SR), \ t_val=slider(0,10,0.2,6, label="Length of curves"), \ u_percent=slider(0,1,0.05,label="<font color='red'>u</font>", default=.7), v_percent=slider(0,1,0.05,label="<font color='blue'>v</font>", default=.7), u_range=input_box(range(-5,5,1), label="u lines"), v_range=input_box(range(-5,5,1), label="v lines")): thickness=4 u_val = min(u_range)+(max(u_range)-min(u_range))*u_percent v_val = min(v_range)+(max(v_range)-min(v_range))*v_percent t_min = -t_val t_max = t_val g1=sum([parametric_plot((SR(u.subs(u=i))._fast_float_('v'),v.subs(u=i)._fast_float_('v')), t_min,t_max, rgbcolor=(1,0,0)) for i in u_range]) g2=sum([parametric_plot((u.subs(v=i)._fast_float_('u'),SR(v.subs(v=i))._fast_float_('u')), t_min,t_max, rgbcolor=(0,0,1)) for i in v_range]) vline_straight=parametric_plot((SR(u.subs(v=v_val))._fast_float_('u'),SR(v.subs(v=v_val))._fast_float_('u')), t_min,t_max, rgbcolor=(0,0,1), linestyle='-',thickness=thickness) uline_straight=parametric_plot((SR(u.subs(u=u_val))._fast_float_('v'),SR(v.subs(u=u_val))._fast_float_('v')), t_min,t_max,rgbcolor=(1,0,0), linestyle='-',thickness=thickness) |
from functools import partial @interact def trans(x=input_box(u2-v2, label="x=",type=SR), \ y=input_box(u*v+cos(u*v), label="y=",type=SR), \ t_val=slider(0,10,0.2,6, label="Length of curves"), \ u_percent=slider(0,1,0.05,label="<font color='red'>u</font>", default=.7), v_percent=slider(0,1,0.05,label="<font color='blue'>v</font>", default=.7), u_range=input_box(range(-5,5,1), label="u lines"), v_range=input_box(range(-5,5,1), label="v lines")): thickness=4 u_val = min(u_range)+(max(u_range)-min(u_range))*u_percent v_val = min(v_range)+(max(v_range)-min(v_range))*v_percent t_min = -t_val t_max = t_val g1=sum([parametric_plot((i,v), t_min,t_max, rgbcolor=(1,0,0)) for i in u_range]) g2=sum([parametric_plot((u,i), t_min,t_max, rgbcolor=(0,0,1)) for i in v_range]) vline_straight=parametric_plot((u,v_val), t_min,t_max, rgbcolor=(0,0,1), linestyle='-',thickness=thickness) uline_straight=parametric_plot((u_val, v), t_min,t_max,rgbcolor=(1,0,0), linestyle='-',thickness=thickness) |
| Line 264: | Line 475: |
g3=sum([parametric_plot((x.subs(u=i)._fast_float_('v'),y.subs(u=i)._fast_float_('v')), t_min,t_max, rgbcolor=(1,0,0)) for i in u_range]) g4=sum([parametric_plot((x.subs(v=i)._fast_float_('u'),y.subs(v=i)._fast_float_('u')), t_min,t_max, rgbcolor=(0,0,1)) for i in v_range]) vline=parametric_plot((SR(x.subs(v=v_val))._fast_float_('u'),SR(y.subs(v=v_val))._fast_float_('u')), t_min,t_max, rgbcolor=(0,0,1), linestyle='-',thickness=thickness) uline=parametric_plot((SR(x.subs(u=u_val))._fast_float_('v'),SR(y.subs(u=u_val))._fast_float_('v')), t_min,t_max,rgbcolor=(1,0,0), linestyle='-',thickness=thickness) (g3+g4+vline+uline).save("xy_coord.png", aspect_ratio=1, figsize=[5,5], axes_labels=['$x$','$y$']) print jsmath("x=%s, \: y=%s"%(latex(x), latex(y))) print "<html><table><tr><td><img src='cell://uv_coord.png'/></td><td><img src='cell://xy_coord.png'/></td></tr></table></html>" }}} attachment:coordinate-transform-1.png attachment:coordinate-transform-2.png |
xuv = fast_float(x,'u','v') yuv = fast_float(y,'u','v') xvu = fast_float(x,'v','u') yvu = fast_float(y,'v','u') g3=sum([parametric_plot((partial(xuv,i),partial(yuv,i)), t_min,t_max, rgbcolor=(1,0,0)) for i in u_range]) g4=sum([parametric_plot((partial(xvu,i),partial(yvu,i)), t_min,t_max, rgbcolor=(0,0,1)) for i in v_range]) vline=parametric_plot((partial(xvu,v_val),partial(yvu,v_val)), t_min,t_max, rgbcolor=(0,0,1), linestyle='-',thickness=thickness) uline=parametric_plot((partial(xuv,u_val),partial(yuv,u_val)), t_min,t_max,rgbcolor=(1,0,0), linestyle='-',thickness=thickness) (g3+g4+vline+uline).save("xy_coord.png", aspect_ratio=1, figsize=[5,5], axes_labels=['$x$','$y$']) print jsmath("x=%s, \: y=%s"%(latex(x), latex(y))) print "<html><table><tr><td><img src='cell://uv_coord.png'/></td><td><img src='cell://xy_coord.png'/></td></tr></table></html>" }}} {{attachment:coordinate-transform-1.png}} {{attachment:coordinate-transform-2.png}} |
| Line 282: | Line 493: |
| Line 296: | Line 508: |
| attachment:taylor_series_animated.gif | {{attachment:taylor_series_animated.gif}} == Illustration of the precise definition of a limit == by John Perry I'll break tradition and put the image first. Apologies if this is Not A Good Thing. {{attachment:snapshot_epsilon_delta.png}} {{{ html("<h2>Limits: <i>ε-δ</i></h2>") html("This allows you to estimate which values of <i>δ</i> guarantee that <i>f</i> is within <i>ε</i> units of a limit.") html("<ul><li>Modify the value of <i>f</i> to choose a function.</li>") html("<li>Modify the value of <i>a</i> to change the <i>x</i>-value where the limit is being estimated.</li>") html("<li>Modify the value of <i>L</i> to change your guess of the limit.</li>") html("<li>Modify the values of <i>δ</i> and <i>ε</i> to modify the rectangle.</li></ul>") html("If the blue curve passes through the pink boxes, your values for <i>δ</i> and/or <i>ε</i> are probably wrong.") @interact def delta_epsilon(f = input_box(default=(x^2-x)/(x-1)), a=input_box(default=1), L = input_box(default=1), delta=input_box(label="δ",default=0.1), epsilon=input_box(label="ε",default=0.1), xm=input_box(label="<i>x</i><sub>min</sub>",default=-1), xM=input_box(label="<i>x</i><sub>max</sub>",default=4)): f_left_plot = plot(f,xm,a-delta/3,thickness=2) f_right_plot = plot(f,a+delta/3,xM,thickness=2) epsilon_line_1 = line([(xm,L-epsilon),(xM,L-epsilon)], rgbcolor=(0.5,0.5,0.5),linestyle='--') epsilon_line_2 = line([(xm,L+epsilon),(xM,L+epsilon)], rgbcolor=(0.5,0.5,0.5),linestyle='--') ym = min(f_right_plot.ymin(),f_left_plot.ymin()) yM = max(f_right_plot.ymax(),f_left_plot.ymax()) bad_region_1 = polygon([(a-delta,L+epsilon),(a-delta,yM),(a+delta,yM),(a+delta,L+epsilon)], rgbcolor=(1,0.6,0.6)) bad_region_2 = polygon([(a-delta,L-epsilon),(a-delta,ym),(a+delta,ym),(a+delta,L-epsilon)], rgbcolor=(1,0.6,0.6)) aL_point = point((a,L),rgbcolor=(1,0,0),pointsize=20) delta_line_1 = line([(a-delta,ym),(a-delta,yM)],rgbcolor=(0.5,0.5,0.5),linestyle='--') delta_line_2 = line([(a+delta,ym),(a+delta,yM)],rgbcolor=(0.5,0.5,0.5),linestyle='--') (f_left_plot +f_right_plot +epsilon_line_1 +epsilon_line_2 +delta_line_1 +delta_line_2 +aL_point +bad_region_1 +bad_region_2).show(xmin=xm,xmax=xM) }}} == A graphical illustration of sin(x)/x -> 1 as x-> 0 == by Wai Yan Pong {{{ x=var('x') @interact def _(x = slider(-7/10,7/10,1/20,1/2)): html('<h3>A graphical illustration of $\lim_{x -> 0} \sin(x)/x =1$</h3>') html('Below is the unit circle, so the length of the <font color=red>red line</font> is |sin(x)|') html('and the length of the <font color=blue>blue line</font> is |tan(x)| where x is the length of the arc.') html('From the picture, we see that |sin(x)| $\le$ |x| $\le$ |tan(x)|.') html('It follows easily from this that cos(x) $\le$ sin(x)/x $\le$ 1 when x is near 0.') html('As $\lim_{x ->0} \cos(x) =1$, we conclude that $\lim_{x -> 0} \sin(x)/x =1$.') if not (x == 0): pretty_print("sin(x)/x = "+str(sin(float(x))/float(x))) elif x == 0: pretty_print("The limit of sin(x)/x as x tends to 0 is 1.") C=circle((0,0),1, rgbcolor='black') mvp = (cos(x),sin(x));tpt = (1, tan(x)) p1 = point(mvp, pointsize=30, rgbcolor='red'); p2 = point((1,0), pointsize=30, rgbcolor='red') line1 = line([(0,0),tpt], rgbcolor='black'); line2 = line([(cos(x),0),mvp], rgbcolor='red') line3 = line([(0,0),(1,0)], rgbcolor='black'); line4 = line([(1,0),tpt], rgbcolor='blue') result = C+p1+p2+line1+line2+line3+line4 result.show(aspect_ratio=1, figsize=[3,3], axes=False) }}} {{attachment:sinelimit.png}} == Quadric Surface Plotter == by Marshall Hampton. This is pretty simple, so I encourage people to spruce it up. In particular, it isn't set up to show all possible types of quadrics. {{{ var('x,y,z') quadrics = {'Ellipsoid':x^2+y^2+z^2-1,'Elliptic paraboloid':x^2+y^2-z,'Hyperbolic paraboloid':x^2-y^2-z, '1-Sheeted Hyperboloid':x^2+y^2-z^2-1,'2-Sheeted Hyperboloid':x^2-y^2-z^2-1, 'Cone':x^2+y^2-z^2} @interact def quads(q = selector(quadrics.keys()), a = slider(0,5,1/2,default = 1)): f = quadrics[q].subs({x:x*a^(1/2)}) if a==0 or q=='Cone': html('<center>$'+latex(f)+' \ $'+ '(degenerate)</center>') else: html('<center>$'+latex(f)+'$ </center>') p = implicit_plot3d(f,(x,-2,2),(y,-2,2),(z,-2,2), plot_points = 75) show(p) }}} {{attachment:quadrics.png}} == The midpoint rule for numerically integrating a function of two variables == by Marshall Hampton {{{ from sage.plot.plot3d.platonic import index_face_set def cuboid(v1,v2,**kwds): """ Cuboid defined by corner points v1 and v2. """ ptlist = [] for vi in (v1,v2): for vj in (v1,v2): for vk in (v1,v2): ptlist.append([vi[0],vj[1],vk[2]]) f_incs = [[0, 2, 6, 4], [0, 1, 3, 2], [0, 1, 5, 4], [1, 3, 7, 5], [2, 3, 7, 6], [4, 5, 7, 6]] if 'aspect_ratio' not in kwds: kwds['aspect_ratio'] = [1,1,1] return index_face_set(f_incs,ptlist,enclosed = True, **kwds) var('x,y') R16 = RealField(16) npi = RDF(pi) sin,cos = math.sin,math.cos html("<h1>The midpoint rule for a function of two variables</h1>") @interact def midpoint2d(func = input_box('y*sin(x)/x+sin(y)',type=str,label='function of x and y'), nx = slider(2,20,1,3,label='x subdivisions'), ny = slider(2,20,1,3,label='y subdivisions'), x_start = slider(-10,10,.1,0), x_end = slider(-10,10,.1,3*npi), y_start= slider(-10,10,.1,0), y_end= slider(-10,10,.1,3*npi)): f = sage_eval('lambda x,y: ' + func) delx = (x_end - x_start)/nx dely = (y_end - y_start)/nx xvals = [RDF(x_start + (i+1.0/2)*delx) for i in range(nx)] yvals = [RDF(y_start + (i+1.0/2)*dely) for i in range(ny)] num_approx = 0 cubs = [] darea = delx*dely for xv in xvals: for yv in yvals: num_approx += f(xv,yv)*darea cubs.append(cuboid([xv-delx/2,yv-dely/2,0],[xv+delx/2,yv+dely/2,f(xv,yv)], opacity = .5, rgbcolor = (1,0,0))) html("$$\int_{"+str(R16(y_start))+"}^{"+str(R16(y_end))+"} "+ "\int_{"+str(R16(x_start))+"}^{"+str(R16(x_end))+"} "+func+"\ dx \ dy$$") html('<p style="text-align: center;">Numerical approximation: ' + str(num_approx)+'</p>') p1 = plot3d(f,(x,x_start,x_end),(y,y_start,y_end)) show(p1+sum(cubs)) }}} {{attachment:numint2d.png}} == Gaussian (Legendre) quadrature == by Jason Grout The output shows the points evaluated using Gaussian quadrature (using a weight of 1, so using Legendre polynomials). The vertical bars are shaded to represent the relative weights of the points (darker = more weight). The error in the trapezoid, Simpson, and quadrature methods is both printed out and compared through a bar graph. The "Real" error is the error returned from scipy on the definite integral. {{{ from scipy.special.orthogonal import p_roots from scipy.integrate import quad, trapz, simps from sage.ext.fast_eval import fast_float from numpy import linspace show_weight_graph=False # 'Hermite': {'w': e**(-x**2), 'xmin': -numpy.inf, 'xmax': numpy.inf, 'func': h_roots}, # 'Laguerre': {'w': e**(-x), 'xmin': 0, 'xmax': numpy.inf, 'func': l_roots}, methods = {'Legendre': {'w': 1, 'xmin': -1, 'xmax': 1, 'func': p_roots}, 'Chebyshev': {'w': 1/sqrt(1-x**2), 'xmin': -1, 'xmax': 1, 'func': t_roots}, 'Chebyshev2': {'w': sqrt(1-x**2), 'xmin': -1, 'xmax': 1, 'func': u_roots}, 'Trapezoid': {'w': 1, 'xmin': -1, 'xmax': 1, 'func': lambda n: (linspace(-1r,1,n), numpy.array([1.0r]+[2.0r]*(n-2)+[1.0r])*1.0r/n)}, 'Simpson': {'w': 1, 'xmin': -1, 'xmax': 1, 'func': lambda n: (linspace(-1r,1,n), numpy.array([1.0r]+[4.0r,2.0r]*int((n-3.0r)/2.0r)+[4.0r,1.0r])*2.0r/(3.0r*n))}} var("x") def box(center, height, area,**kwds): width2 = 1.0*area/height/2.0 return polygon([(center-width2,0),(center+width2,0),(center+width2,height),(center-width2,height)],**kwds) @interact def weights(n=slider(1,30,1,default=10),f=input_box(default=3*x+cos(10*x)),show_method=["Legendre", "Chebyshev", "Chebyshev2", "Trapezoid","Simpson"]): ff = fast_float(f,'x') method = methods[show_method] xcoords,w = (method['func'])(int(n)) xmin = method['xmin'] xmax = method['xmax'] plot_min = max(xmin, -10) plot_max = min(xmax, 10) scaled_func = f*method['w'] scaled_ff = fast_float(scaled_func) coords = zip(xcoords,w) max_weight = max(w) coords_scaled = zip(xcoords,w/max_weight) f_graph = plot(scaled_func,plot_min,plot_max) boxes = sum(box(x,ff(x),w*ff(x),rgbcolor=(0.5,0.5,0.5),alpha=0.3) for x,w in coords) stems = sum(line([(x,0),(x,scaled_ff(x))],rgbcolor=(1-y,1-y,1-y),thickness=2,markersize=6,alpha=y) for x,y in coords_scaled) points = sum([point([(x,0),(x,scaled_ff(x))],rgbcolor='black',pointsize=30) for x,_ in coords]) graph = stems+points+f_graph+boxes if show_weight_graph: graph += line([(x,y) for x,y in coords_scaled], rgbcolor='green',alpha=0.4) show(graph,xmin=plot_min,xmax=plot_max) approximation = sum([w*ff(x) for x,w in coords]) integral,integral_error = scipy.integrate.quad(scaled_ff, xmin, xmax) x_val = linspace(min(xcoords), max(xcoords),n) y_val = map(scaled_ff,x_val) trapezoid = integral-trapz(y_val, x_val) simpson = integral-simps(y_val, x_val) html("$$\sum_{i=1}^{i=%s}w_i\left(%s\\right)= %s\\approx %s =\int_{-1}^{1}%s \,dx$$"%(n,latex(f.subs(x="x_i")), approximation, integral, latex(scaled_func))) error_data = [trapezoid, simpson, integral-approximation,integral_error] print "Trapezoid: %s, Simpson: %s, \nMethod: %s, Real: %s"%tuple(error_data) show(bar_chart(error_data,width=1),ymin=min(error_data), ymax=max(error_data)) }}} {{attachment:quadrature1.png}} {{attachment:quadrature2.png}} == Vector Calculus, 2-D Motion == By Rob Beezer A fast_float() version is available in a [[http://buzzard.ups.edu/sage/motion-2d.sws|worksheet]] {{{ # 2-D motion and vector calculus # Copyright 2009, Robert A. Beezer # Creative Commons BY-SA 3.0 US # # 2009/02/15 Built on Sage 3.3.rc0 # 2009/02/17 Improvements from Jason Grout # # variable parameter is t # later at a particular value named t0 # var('t') # # parameter range # start=0 stop=2*pi # # position vector definition # edit here for new example # example is wide ellipse # adjust x, extents in final show() # position=vector( (4*cos(t), sin(t)) ) # # graphic of the motion itself # path = parametric_plot( position(t).list(), (t, start, stop), color = "black" ) # # derivatives of motion, lengths, unit vectors, etc # velocity = derivative( position(t) ) acceleration = derivative(velocity(t)) speed = velocity.norm() speed_deriv = derivative(speed) tangent = (1/speed)*velocity dT = derivative(tangent(t)) normal = (1/dT.norm())*dT # # interact section # slider for parameter, 24 settings # checkboxes for various vector displays # computations at one value of parameter, t0 # @interact def _(t0 = slider(float(start), float(stop), float((stop-start)/24), float(start) , label = "Parameter"), pos_check = ("Position", True), vel_check = ("Velocity", False), tan_check = ("Unit Tangent", False), nor_check = ("Unit Normal", False), acc_check = ("Acceleration", False), tancomp_check = ("Tangential Component", False), norcomp_check = ("Normal Component", False) ): # # location of interest # pos_tzero = position(t0) # # various scalar quantities at point # speed_component = speed(t0) tangent_component = speed_deriv(t0) normal_component = sqrt( acceleration(t0).norm()^2 - tangent_component^2 ) curvature = normal_component/speed_component^2 # # various vectors, mostly as arrows from the point # pos = arrow((0,0), pos_tzero, rgbcolor=(0,0,0)) tan = arrow(pos_tzero, pos_tzero + tangent(t0), rgbcolor=(0,1,0) ) vel = arrow(pos_tzero, pos_tzero + velocity(t0), rgbcolor=(0,0.5,0)) nor = arrow(pos_tzero, pos_tzero + normal(t0), rgbcolor=(0.5,0,0)) acc = arrow(pos_tzero, pos_tzero + acceleration(t0), rgbcolor=(1,0,1)) tancomp = arrow(pos_tzero, pos_tzero + tangent_component*tangent(t0), rgbcolor=(1,0,1) ) norcomp = arrow(pos_tzero, pos_tzero + normal_component*normal(t0), rgbcolor=(1,0,1)) # # accumulate the graphic based on checkboxes # picture = path if pos_check: picture = picture + pos if vel_check: picture = picture + vel if tan_check: picture = picture+ tan if nor_check: picture = picture + nor if acc_check: picture = picture + acc if tancomp_check: picture = picture + tancomp if norcomp_check: picture = picture + norcomp # # print textual info # print "Position vector defined as r(t)=", position(t) print "Speed is ", N(speed(t0)) print "Curvature is ", N(curvature) # # show accumulated graphical info # adjust x-,y- extents to get best plot # show(picture, xmin=-4,xmax=4, ymin=-1.5,ymax=1.5,aspect_ratio=1) }}} {{attachment:motion2d.png}} == Vector Calculus, 3-D Motion == by Rob Beezer Available as a [[http://buzzard.ups.edu/sage/motion-d.sws|worksheet]] {{{ # 3-D motion and vector calculus # Copyright 2009, Robert A. Beezer # Creative Commons BY-SA 3.0 US # # # 2009/02/15 Built on Sage 3.3.rc0 # 2009/02/17 Improvements from Jason Grout # # variable parameter is t # later at a particular value named t0 # # un-comment double hash (##) to get # time-consuming torsion computation # var('t') # # parameter range # start=-4*pi stop=8*pi # # position vector definition # edit here for new example # example is wide ellipse # adjust figsize in final show() to get accurate aspect ratio # a=1/(8*pi) c=(3/2)*a position=vector( (exp(a*t)*cos(t), exp(a*t)*sin(t), exp(c*t)) ) # # graphic of the motion itself # path = parametric_plot3d( position(t).list(), (t, start, stop), color = "black" ) # # derivatives of motion, lengths, unit vectors, etc # velocity = derivative( position(t) ) acceleration = derivative(velocity(t)) speed = velocity.norm() speed_deriv = derivative(speed) tangent = (1/speed)*velocity dT = derivative(tangent(t)) normal = (1/dT.norm())*dT binormal = tangent.cross_product(normal) ## dB = derivative(binormal(t)) # # interact section # slider for parameter, 24 settings # checkboxes for various vector displays # computations at one value of parameter, t0 # @interact def _(t0 = slider(float(start), float(stop), float((stop-start)/24), float(start) , label = "Parameter"), pos_check = ("Position", True), vel_check = ("Velocity", False), tan_check = ("Unit Tangent", False), nor_check = ("Unit Normal", False), bin_check = ("Unit Binormal", False), acc_check = ("Acceleration", False), tancomp_check = ("Tangential Component", False), norcomp_check = ("Normal Component", False) ): # # location of interest # pos_tzero = position(t0) # # various scalar quantities at point # speed_component = speed(t0) tangent_component = speed_deriv(t0) normal_component = sqrt( acceleration(t0).norm()^2 - tangent_component^2 ) curvature = normal_component/speed_component^2 ## torsion = (1/speed_component)*(dB(t0)).dot_product(normal(t0)) # # various vectors, mostly as arrows from the point # pos = arrow3d((0,0,0), pos_tzero, rgbcolor=(0,0,0)) tan = arrow3d(pos_tzero, pos_tzero + tangent(t0), rgbcolor=(0,1,0) ) vel = arrow3d(pos_tzero, pos_tzero + velocity(t0), rgbcolor=(0,0.5,0)) nor = arrow3d(pos_tzero, pos_tzero + normal(t0), rgbcolor=(0.5,0,0)) bin = arrow3d(pos_tzero, pos_tzero + binormal(t0), rgbcolor=(0,0,0.5)) acc = arrow3d(pos_tzero, pos_tzero + acceleration(t0), rgbcolor=(1,0,1)) tancomp = arrow3d(pos_tzero, pos_tzero + tangent_component*tangent(t0), rgbcolor=(1,0,1) ) norcomp = arrow3d(pos_tzero, pos_tzero + normal_component*normal(t0), rgbcolor=(1,0,1)) # # accumulate the graphic based on checkboxes # picture = path if pos_check: picture = picture + pos if vel_check: picture = picture + vel if tan_check: picture = picture+ tan if nor_check: picture = picture + nor if bin_check: picture = picture + bin if acc_check: picture = picture + acc if tancomp_check: picture = picture + tancomp if norcomp_check: picture = picture + norcomp # # print textual info # print "Position vector: r(t)=", position(t) print "Speed is ", N(speed(t0)) print "Curvature is ", N(curvature) ## print "Torsion is ", N(torsion) print "Right-click on graphic to zoom to 400%" print "Drag graphic to rotate" # # show accumulated graphical info # show(picture, aspect_ratio=[1,1,1]) }}} {{attachment:motion3d.png}} == Directional Derivatives == This interact displays graphically a tangent line to a function, illustrating a directional derivative (the slope of the tangent line). {{{ var('x,y,t,z') f(x,y)=sin(x)*cos(y) pif = float(pi) line_thickness=3 surface_color='blue' plane_color='purple' line_color='red' tangent_color='green' gradient_color='orange' @interact def myfun(location=input_grid(1, 2, default=[0,0], label = "Location (x,y)", width=2), angle=slider(0, 2*pif, label = "Angle"), show_surface=("Show surface", True)): location3d = vector(location[0]+[0]) location = location3d[0:2] direction3d = vector(RDF, [cos(angle), sin(angle), 0]) direction=direction3d[0:2] cos_angle = math.cos(angle) sin_angle = math.sin(angle) df = f.gradient() direction_vector=line3d([location3d, location3d+direction3d], arrow_head=True, rgbcolor=line_color, thickness=line_thickness) curve_point = (location+t*direction).list() curve = parametric_plot(curve_point+[f(*curve_point)], (t,-3,3),color=line_color,thickness=line_thickness) plane = parametric_plot((cos_angle*x+location[0],sin_angle*x+location[1],t), (x, -3,3), (t,-3,3),opacity=0.8, color=plane_color) pt = point3d(location3d.list(),color='green', size=10) tangent_line = parametric_plot((location[0]+t*cos_angle, location[1]+t*sin_angle, f(*location)+t*df(*location)*(direction)), (t, -3,3), thickness=line_thickness, color=tangent_color) picture3d = direction_vector+curve+plane+pt+tangent_line picture2d = contour_plot(f(x,y), (x,-3,3),(y,-3,3), plot_points=100) picture2d += arrow(location.list(), (location+direction).list()) picture2d += point(location.list(),rgbcolor='green',pointsize=40) if show_surface: picture3d += plot3d(f, (x,-3,3),(y,-3,3),opacity=0.7) dff = df(location[0], location[1]) dff3d = vector(RDF,dff.list()+[0]) picture3d += line3d([location3d, location3d+dff3d], arrow_head=True, rgbcolor=gradient_color, thickness=line_thickness) picture2d += arrow(location.list(), (location+dff).list(), rgbcolor=gradient_color, width=line_thickness) show(picture3d,aspect=[1,1,1], axes=True) show(picture2d, aspect_ratio=1) }}} {{attachment:directional derivative.png}} == 3D graph with points and curves == By Robert Marik This sagelet is handy when showing local, constrained and absolute maxima and minima in two variables. Available as a [[http://user.mendelu.cz/marik/sage/3Dgraph_with_points.sws|worksheet]] {{{ %hide %auto x,y, t, u, v =var('x y t u v') INI_func='x^2-2*x+y^2-2*y' INI_box='-1,3.2,-1,3.2' INI_points='(1,1,\'green\'),(3/2,3/2),(0,1),(1,0),(0,0,\'black\'),(3,0,\'black\'),(0,3,\'black\')' INI_curves='(t,0,0,3,\'red\'),(0,t,0,3,\'green\'),(t,3-t,0,3)' @interact def _(func=input_box(INI_func,label="f(x,y)=",type=str),\ bounds=input_box(INI_box,label="xmin,xmax,ymin,ymax",type=str),\ st_points=input_box(INI_points,\ label="points <br><small><small>(comma separated pairs, optionally with color)</small></small>", type=str),\ bnd_curves=input_box(INI_curves,label="curves on boundary<br> <small><small><i>(x(t),y(t),tmin,tmax,'opt_color')</i></small></small>", type=str),\ show_planes=("Show zero planes", False), show_axes=("Show axes", True), show_table=("Show table", True)): f=sage_eval('lambda x,y: ' + func) html(r'Function $ f(x,y)=%s$ '%latex(f(x,y))) xmin,xmax,ymin,ymax=sage_eval('('+bounds+')') A=plot3d(f(x,y),(x,xmin,xmax),(y,ymin,ymax),opacity=0.5) if not(bool(st_points=='')): st_p=sage_eval('('+st_points+',)') html(r'<table border=1>') for current in range(len(st_p)): point_color='red' if bool(len(st_p[current])==3): point_color=st_p[current][2] x0=st_p[current][0] y0=st_p[current][1] z0=f(x0,y0) if show_table: html(r'<tr><td>$\quad f(%s,%s)\quad $</td><td>$\quad %s$</td>\ </tr>'%(latex(x0),latex(y0),z0.n())) A=A+point3d((x0,y0,z0),size=9,rgbcolor=point_color) html(r'</table>') if not(bool(bnd_curves=='')): bnd_cc=sage_eval('('+bnd_curves+',)',locals={'t':t}) for current in range(len(bnd_cc)): bnd_c=bnd_cc[current]+('black',) A=A+parametric_plot3d((bnd_c[0],bnd_c[1],f(bnd_c[0],bnd_c[1])),\ (t,bnd_c[2],bnd_c[3]),thickness=3,rgbcolor=bnd_c[4]) if show_planes: A=A+plot3d(0,(x,xmin,xmax),(y,ymin,ymax),opacity=0.3,rgbcolor='gray') zmax=A.bounding_box()[1][2] zmin=A.bounding_box()[0][2] A=A+parametric_plot3d((u,0,v),(u,xmin,xmax),(v,zmin,zmax),opacity=0.3,rgbcolor='gray') A=A+parametric_plot3d((0,u,v),(u,ymin,ymax),(v,zmin,zmax),opacity=0.3,rgbcolor='gray') if show_axes: zmax=A.bounding_box()[1][2] zmin=A.bounding_box()[0][2] A=A+line3d([(xmin,0,0), (xmax,0,0)], arrow_head=True,rgbcolor='black') A=A+line3d([(0,ymin,0), (0,ymax,0)], arrow_head=True,rgbcolor='black') A=A+line3d([(0,0,zmin), (0,0,zmax)], arrow_head=True,rgbcolor='black') show(A) }}} {{attachment:3Dgraph_with_points.png}} == Approximating function in two variables by differential == by Robert Marik {{{ x,y=var('x y') html('<h2>Explaining approximation of a function in two \ variables by differential</h2>') html('Points x0 and y0 are values where the exact value of the function \ is known. Deltax and Deltay are displacements of the new point. Exact value \ and approximation by differential at shifted point are compared.') @interact def _(func=input_box('sqrt(x^3+y^3)',label="f(x,y)=",type=str), x0=1, y0=2, \ deltax=slider(-1,1,0.01,0.2),\ deltay=slider(-1,1,0.01,-0.4), xmin=0, xmax=2, ymin=0, ymax=3): f=sage_eval('lambda x,y: ' + func) derx(x,y)=diff(f(x,y),x) dery(x,y)=diff(f(x,y),y) tangent(x,y)=f(x0,y0)+derx(x0,y0)*(x-x0)+dery(x0,y0)*(y-y0) A=plot3d(f(x,y),(x,xmin,xmax),(y,ymin,ymax),opacity=0.5) B=plot3d(tangent(x,y),(x,xmin,xmax),(y,ymin,ymax),color='red',opacity=0.5) C=point3d((x0,y0,f(x0,y0)),rgbcolor='blue',size=9) CC=point3d((x0+deltax,y0+deltay,f(x0+deltax,y0+deltay)),rgbcolor='blue',size=9) D=point3d((x0+deltax,y0+deltay,tangent(x0+deltax,y0+deltay)),rgbcolor='red',size=9) exact_value_ori=f(x0,y0).n(digits=10) exact_value=f(x0+deltax,y0+deltay) approx_value=tangent(x0+deltax,y0+deltay).n(digits=10) abs_error=(abs(exact_value-approx_value)) html(r'Function $ f(x,y)=%s \approx %s $ '%(latex(f(x,y)),latex(tangent(x,y)))) html(r' $f %s = %s$'%(latex((x0,y0)),latex(exact_value_ori))) html(r'Shifted point $%s$'%latex(((x0+deltax),(y0+deltay)))) html(r'Value of the function in shifted point is $%s$'%f(x0+deltax,y0+deltay)) html(r'Value on the tangent plane in shifted point is $%s$'%latex(approx_value)) html(r'Error is $%s$'%latex(abs_error)) show(A+B+C+CC+D) }}} {{attachment:3D_differential.png}} == Taylor approximations in two variables == by John Palmieri This displays the nth order Taylor approximation, for n from 1 to 10, of the function sin(x^2^ + y^2^) cos(y) exp(-(x^2^+y^2^)/2). {{{ var('x y') var('xx yy') G = sin(xx^2 + yy^2) * cos(yy) * exp(-0.5*(xx^2+yy^2)) def F(x,y): return G.subs(xx=x).subs(yy=y) plotF = plot3d(F, (0.4, 2), (0.4, 2), adaptive=True, color='blue') @interact def _(x0=(0.5,1.5), y0=(0.5, 1.5), order=(1..10)): F0 = float(G.subs(xx=x0).subs(yy=y0)) P = (x0, y0, F0) dot = point3d(P, size=15, color='red') plot = dot + plotF approx = F0 for n in range(1, order+1): for i in range(n+1): if i == 0: deriv = G.diff(yy, n) elif i == n: deriv = G.diff(xx, n) else: deriv = G.diff(xx, i).diff(yy, n-i) deriv = float(deriv.subs(xx=x0).subs(yy=y0)) coeff = binomial(n, i)/factorial(n) approx += coeff * deriv * (x-x0)^i * (y-y0)^(n-i) plot += plot3d(approx, (x, 0.4, 1.6), (y, 0.4, 1.6), color='red', opacity=0.7) html('$F(x,y) = e^{-(x^2+y^2)/2} \\cos(y) \\sin(x^2+y^2)$') show(plot) }}} {{attachment:taylor-3d.png}} |
Sage Interactions - Calculus
goto interact main page
Contents
-
Sage Interactions - Calculus
- Root Finding Using Bisection
- Newton's Method
- A contour map and 3d plot of two inverse distance functions
- A simple tangent line grapher
- Numerical integrals with the midpoint rule
- Numerical integrals with various rules
- Some polar parametric curves
- Function tool
- Newton-Raphson Root Finding
- Coordinate Transformations
- Taylor Series
- Illustration of the precise definition of a limit
- A graphical illustration of sin(x)/x -> 1 as x-> 0
- Quadric Surface Plotter
- The midpoint rule for numerically integrating a function of two variables
- Gaussian (Legendre) quadrature
- Vector Calculus, 2-D Motion
- Vector Calculus, 3-D Motion
- Directional Derivatives
- 3D graph with points and curves
- Approximating function in two variables by differential
- Taylor approximations in two variables
Root Finding Using Bisection
by William Stein
def bisect_method(f, a, b, eps):
try:
f = f._fast_float_(f.variables()[0])
except AttributeError:
pass
intervals = [(a,b)]
two = float(2); eps = float(eps)
while True:
c = (a+b)/two
fa = f(a); fb = f(b); fc = f(c)
if abs(fc) < eps: return c, intervals
if fa*fc < 0:
a, b = a, c
elif fc*fb < 0:
a, b = c, b
else:
raise ValueError, "f must have a sign change in the interval (%s,%s)"%(a,b)
intervals.append((a,b))
html("<h1>Double Precision Root Finding Using Bisection</h1>")
@interact
def _(f = cos(x) - x, a = float(0), b = float(1), eps=(-3,(-16..-1))):
eps = 10^eps
print "eps = %s"%float(eps)
try:
time c, intervals = bisect_method(f, a, b, eps)
except ValueError:
print "f must have opposite sign at the endpoints of the interval"
show(plot(f, a, b, color='red'), xmin=a, xmax=b)
else:
print "root =", c
print "f(c) = %r"%f(c)
print "iterations =", len(intervals)
P = plot(f, a, b, color='red')
h = (P.ymax() - P.ymin())/ (1.5*len(intervals))
L = sum(line([(c,h*i), (d,h*i)]) for i, (c,d) in enumerate(intervals) )
L += sum(line([(c,h*i-h/4), (c,h*i+h/4)]) for i, (c,d) in enumerate(intervals) )
L += sum(line([(d,h*i-h/4), (d,h*i+h/4)]) for i, (c,d) in enumerate(intervals) )
show(P + L, xmin=a, xmax=b)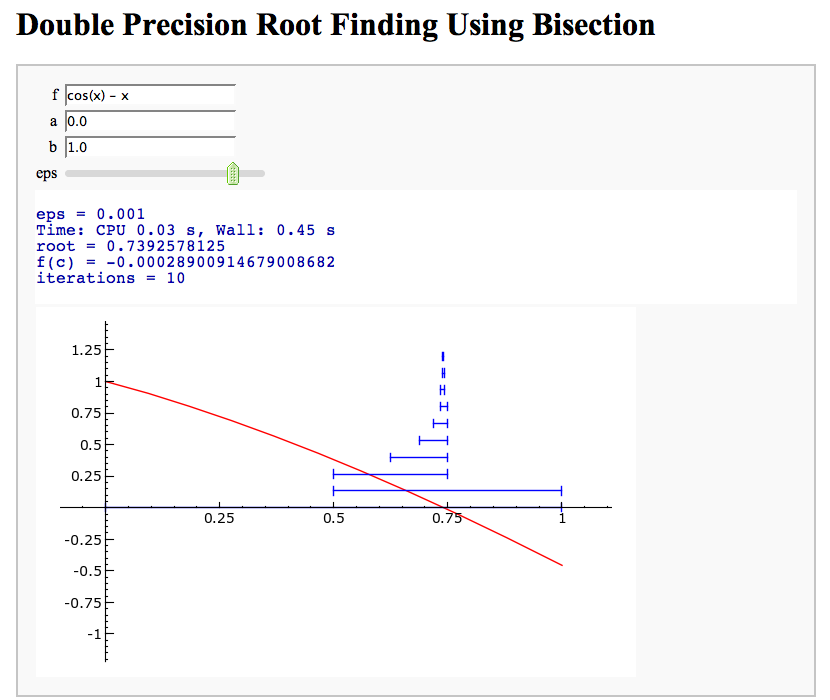
Newton's Method
Note that there is a more complicated Newton's method below.
by William Stein
def newton_method(f, c, eps, maxiter=100):
x = f.variables()[0]
fprime = f.derivative(x)
try:
g = f._fast_float_(x)
gprime = fprime._fast_float_(x)
except AttributeError:
g = f; gprime = fprime
iterates = [c]
for i in xrange(maxiter):
fc = g(c)
if abs(fc) < eps: return c, iterates
c = c - fc/gprime(c)
iterates.append(c)
return c, iterates
html("<h1>Double Precision Root Finding Using Newton's Method</h1>")
@interact
def _(f = x^2 - 2, c = float(0.5), eps=(-3,(-16..-1)), interval=float(0.5)):
eps = 10^(eps)
print "eps = %s"%float(eps)
time z, iterates = newton_method(f, c, eps)
print "root =", z
print "f(c) = %r"%f(z)
n = len(iterates)
print "iterations =", n
html(iterates)
P = plot(f, z-interval, z+interval, rgbcolor='blue')
h = P.ymax(); j = P.ymin()
L = sum(point((w,(n-1-float(i))/n*h), rgbcolor=(float(i)/n,0.2,0.3), pointsize=10) + \
line([(w,h),(w,j)],rgbcolor='black',thickness=0.2) for i,w in enumerate(iterates))
show(P + L, xmin=z-interval, xmax=z+interval)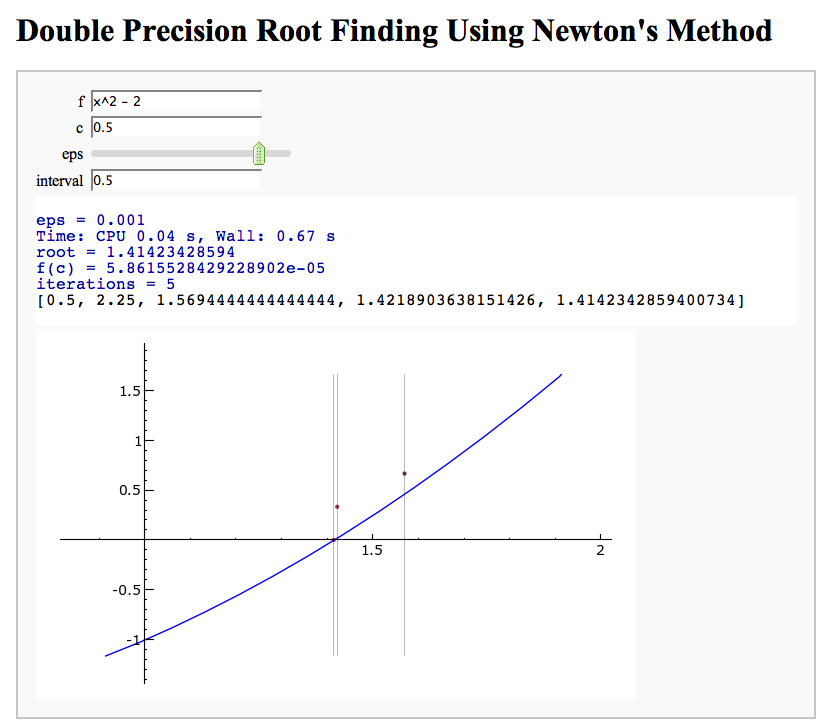
A contour map and 3d plot of two inverse distance functions
by William Stein
@interact
def _(q1=(-1,(-3,3)), q2=(-2,(-3,3)),
cmap=['autumn', 'bone', 'cool', 'copper', 'gray', 'hot', 'hsv',
'jet', 'pink', 'prism', 'spring', 'summer', 'winter']):
x,y = var('x,y')
f = q1/sqrt((x+1)^2 + y^2) + q2/sqrt((x-1)^2+(y+0.5)^2)
C = contour_plot(f, (-2,2), (-2,2), plot_points=30, contours=15, cmap=cmap)
show(C, figsize=3, aspect_ratio=1)
show(plot3d(f, (x,-2,2), (y,-2,2)), figsize=5, viewer='tachyon')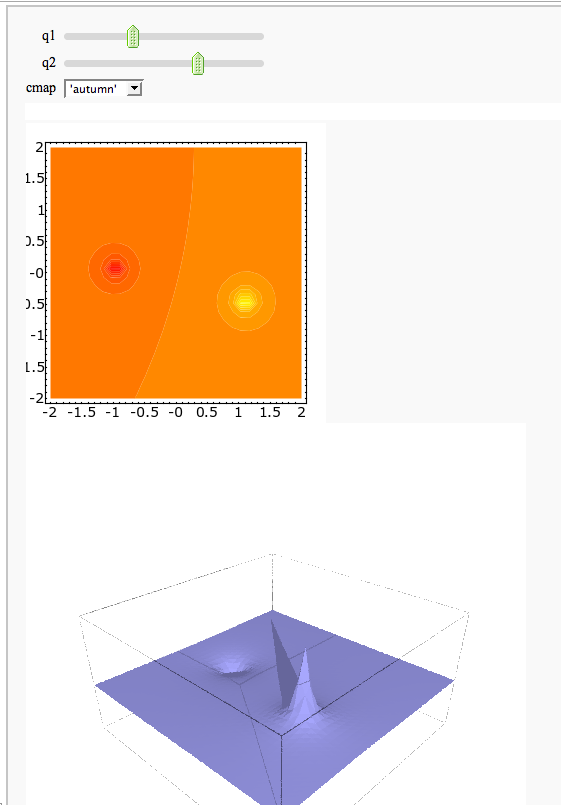
A simple tangent line grapher
by Marshall Hampton
html('<h2>Tangent line grapher</h2>')
@interact
def tangent_line(f = input_box(default=sin(x)), xbegin = slider(0,10,1/10,0), xend = slider(0,10,1/10,10), x0 = slider(0, 1, 1/100, 1/2)):
prange = [xbegin, xend]
x0i = xbegin + x0*(xend-xbegin)
var('x')
df = diff(f)
tanf = f(x0i) + df(x0i)*(x-x0i)
fplot = plot(f, prange[0], prange[1])
print 'Tangent line is y = ' + tanf._repr_()
tanplot = plot(tanf, prange[0], prange[1], rgbcolor = (1,0,0))
fmax = f.find_maximum_on_interval(prange[0], prange[1])[0]
fmin = f.find_minimum_on_interval(prange[0], prange[1])[0]
show(fplot + tanplot, xmin = prange[0], xmax = prange[1], ymax = fmax, ymin = fmin)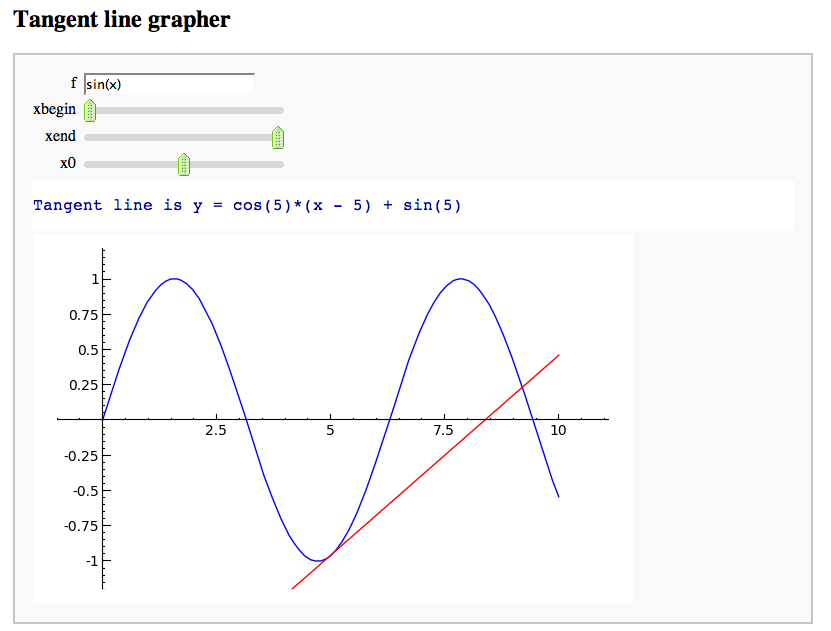
Numerical integrals with the midpoint rule
by Marshall Hampton
var('x')
@interact
def midpoint(n = slider(1,100,1,4), f = input_box(default = "x^2", type = str), start = input_box(default = "0", type = str), end = input_box(default = "1", type = str)):
a = N(start)
b = N(end)
func = sage_eval(f, locals={'x':x})
dx = (b-a)/n
midxs = [q*dx+dx/2 + a for q in range(n)]
midys = [func(x_val) for x_val in midxs]
rects = Graphics()
for q in range(n):
xm = midxs[q]
ym = midys[q]
rects = rects + line([[xm-dx/2,0],[xm-dx/2,ym],[xm+dx/2,ym],[xm+dx/2,0]], rgbcolor = (1,0,0)) + point((xm,ym), rgbcolor = (1,0,0))
min_y = find_minimum_on_interval(func,a,b)[0]
max_y = find_maximum_on_interval(func,a,b)[0]
html('<h3>Numerical integrals with the midpoint rule</h3>')
html('$\int_{a}^{b}{f(x) dx} {\\approx} \sum_i{f(x_i) \Delta x}$')
print "\n\nSage numerical answer: " + str(integral_numerical(func,a,b,max_points = 200)[0])
print "Midpoint estimated answer: " + str(RDF(dx*sum([midys[q] for q in range(n)])))
show(plot(func,a,b) + rects, xmin = a, xmax = b, ymin = min_y, ymax = max_y)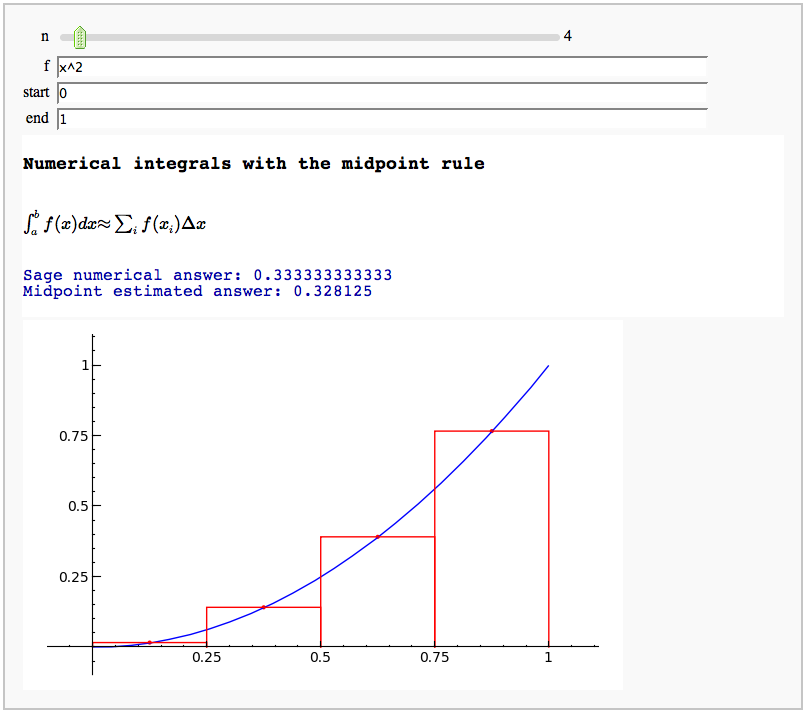
Numerical integrals with various rules
by Nick Alexander (based on the work of Marshall Hampton)
# by Nick Alexander (based on the work of Marshall Hampton)
var('x')
@interact
def midpoint(f = input_box(default = sin(x^2) + 2, type = SR),
interval=range_slider(0, 10, 1, default=(0, 4), label="Interval"),
number_of_subdivisions = slider(1, 20, 1, default=4, label="Number of boxes"),
endpoint_rule = selector(['Midpoint', 'Left', 'Right', 'Upper', 'Lower'], nrows=1, label="Endpoint rule")):
a, b = map(QQ, interval)
t = sage.calculus.calculus.var('t')
func = fast_callable(f(x=t), RDF, vars=[t])
dx = ZZ(b-a)/ZZ(number_of_subdivisions)
xs = []
ys = []
for q in range(number_of_subdivisions):
if endpoint_rule == 'Left':
xs.append(q*dx + a)
elif endpoint_rule == 'Midpoint':
xs.append(q*dx + a + dx/2)
elif endpoint_rule == 'Right':
xs.append(q*dx + a + dx)
elif endpoint_rule == 'Upper':
x = find_maximum_on_interval(func, q*dx + a, q*dx + dx + a)[1]
xs.append(x)
elif endpoint_rule == 'Lower':
x = find_minimum_on_interval(func, q*dx + a, q*dx + dx + a)[1]
xs.append(x)
ys = [ func(x) for x in xs ]
rects = Graphics()
for q in range(number_of_subdivisions):
xm = q*dx + dx/2 + a
x = xs[q]
y = ys[q]
rects += line([[xm-dx/2,0],[xm-dx/2,y],[xm+dx/2,y],[xm+dx/2,0]], rgbcolor = (1,0,0))
rects += point((x, y), rgbcolor = (1,0,0))
min_y = min(0, find_minimum_on_interval(func,a,b)[0])
max_y = max(0, find_maximum_on_interval(func,a,b)[0])
# html('<h3>Numerical integrals with the midpoint rule</h3>')
show(plot(func,a,b) + rects, xmin = a, xmax = b, ymin = min_y, ymax = max_y)
def cap(x):
# print only a few digits of precision
if x < 1e-4:
return 0
return RealField(20)(x)
sum_html = "%s \cdot \\left[ %s \\right]" % (dx, ' + '.join([ "f(%s)" % cap(i) for i in xs ]))
num_html = "%s \cdot \\left[ %s \\right]" % (dx, ' + '.join([ str(cap(i)) for i in ys ]))
numerical_answer = integral_numerical(func,a,b,max_points = 200)[0]
estimated_answer = dx * sum([ ys[q] for q in range(number_of_subdivisions)])
html(r'''
<div class="math">
\begin{align*}
\int_{a}^{b} {f(x) \, dx} & = %s \\\
\sum_{i=1}^{%s} {f(x_i) \, \Delta x}
& = %s \\\
& = %s \\\
& = %s .
\end{align*}
</div>
''' % (numerical_answer, number_of_subdivisions, sum_html, num_html, estimated_answer))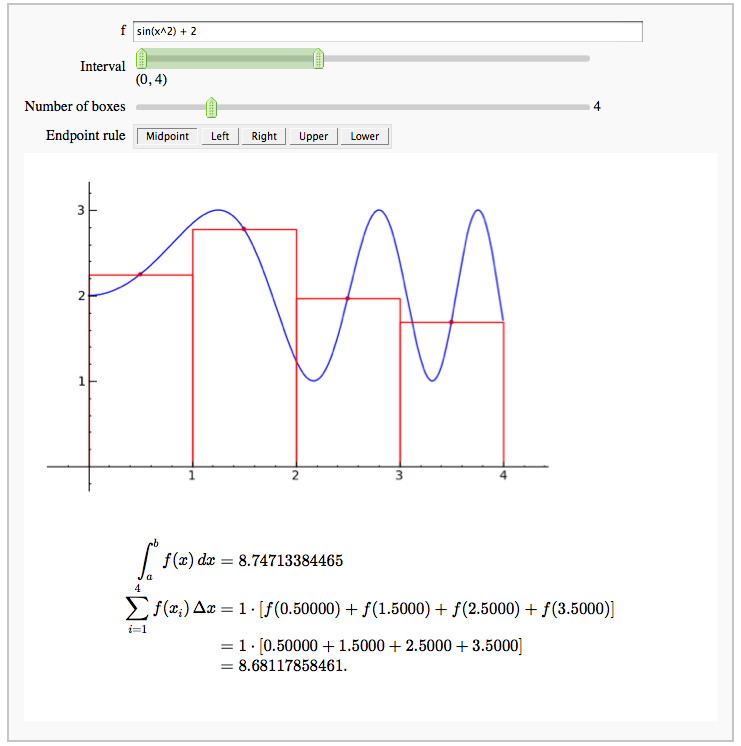
Some polar parametric curves
by Marshall Hampton. This is not very general, but could be modified to show other families of polar curves.
@interact
def para(n1 = slider(1,5,1,default = 2), n2 = slider(1,5,1,default = 3), a1 = slider(1,10,1/10,6/5), a2 = slider(1,10,1/10,6), b = slider(0,2,1/50,0)):
var('t')
html('$r=' + latex(b+sin(a1*t)^n1 + cos(a2*t)^n2)+'$')
p = parametric_plot((cos(t)*(b+sin(a1*t)^n1 + cos(a2*t)^n2), sin(t)*(b+sin(a1*t)^n1 + cos(a2*t)^n2)), (t,0, 20*pi), plot_points = 1024, rgbcolor = (0,0,0))
show(p, figsize = [5,5], xmin = -2-b, xmax = 2+b, ymin = -2-b, ymax = 2+b, axes = False)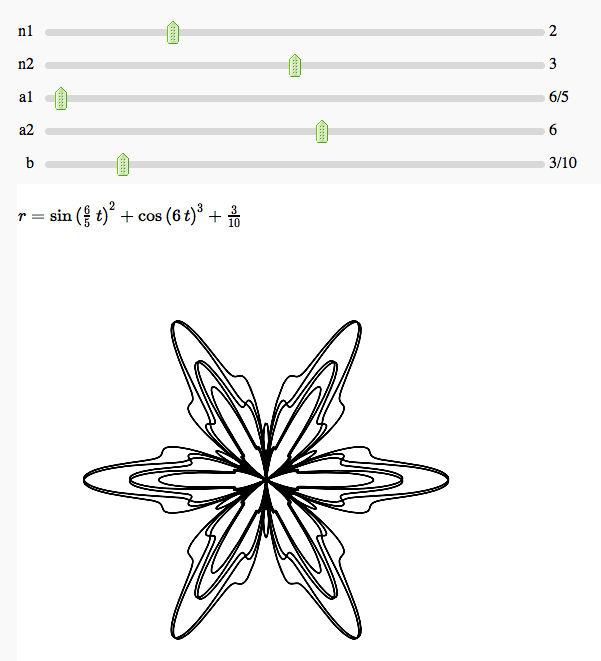
Function tool
Enter symbolic functions f, g, and a, a range, then click the appropriate button to compute and plot some combination of f, g, and a along with f and g. This is inspired by the Matlab funtool GUI.
x = var('x')
@interact
def _(f=sin(x), g=cos(x), xrange=input_box((0,1)), yrange='auto', a=1,
action=selector(['f', 'df/dx', 'int f', 'num f', 'den f', '1/f', 'finv',
'f+a', 'f-a', 'f*a', 'f/a', 'f^a', 'f(x+a)', 'f(x*a)',
'f+g', 'f-g', 'f*g', 'f/g', 'f(g)'],
width=15, nrows=5, label="h = "),
do_plot = ("Draw Plots", True)):
try:
f = SR(f); g = SR(g); a = SR(a)
except TypeError, msg:
print msg[-200:]
print "Unable to make sense of f,g, or a as symbolic expressions."
return
if not (isinstance(xrange, tuple) and len(xrange) == 2):
xrange = (0,1)
h = 0; lbl = ''
if action == 'f':
h = f
lbl = 'f'
elif action == 'df/dx':
h = f.derivative(x)
lbl = '\\frac{df}{dx}'
elif action == 'int f':
h = f.integrate(x)
lbl = '\\int f dx'
elif action == 'num f':
h = f.numerator()
lbl = '\\text{numer(f)}'
elif action == 'den f':
h = f.denominator()
lbl = '\\text{denom(f)}'
elif action == '1/f':
h = 1/f
lbl = '\\frac{1}{f}'
elif action == 'finv':
h = solve(f == var('y'), x)[0].rhs()
lbl = 'f^{-1}(y)'
elif action == 'f+a':
h = f+a
lbl = 'f + a'
elif action == 'f-a':
h = f-a
lbl = 'f - a'
elif action == 'f*a':
h = f*a
lbl = 'f \\times a'
elif action == 'f/a':
h = f/a
lbl = '\\frac{f}{a}'
elif action == 'f^a':
h = f^a
lbl = 'f^a'
elif action == 'f^a':
h = f^a
lbl = 'f^a'
elif action == 'f(x+a)':
h = f(x+a)
lbl = 'f(x+a)'
elif action == 'f(x*a)':
h = f(x*a)
lbl = 'f(xa)'
elif action == 'f+g':
h = f+g
lbl = 'f + g'
elif action == 'f-g':
h = f-g
lbl = 'f - g'
elif action == 'f*g':
h = f*g
lbl = 'f \\times g'
elif action == 'f/g':
h = f/g
lbl = '\\frac{f}{g}'
elif action == 'f(g)':
h = f(g)
lbl = 'f(g)'
html('<center><font color="red">$f = %s$</font></center>'%latex(f))
html('<center><font color="green">$g = %s$</font></center>'%latex(g))
html('<center><font color="blue"><b>$h = %s = %s$</b></font></center>'%(lbl, latex(h)))
if do_plot:
P = plot(f, xrange, color='red', thickness=2) + \
plot(g, xrange, color='green', thickness=2) + \
plot(h, xrange, color='blue', thickness=2)
if yrange == 'auto':
show(P, xmin=xrange[0], xmax=xrange[1])
else:
yrange = sage_eval(yrange)
show(P, xmin=xrange[0], xmax=xrange[1], ymin=yrange[0], ymax=yrange[1])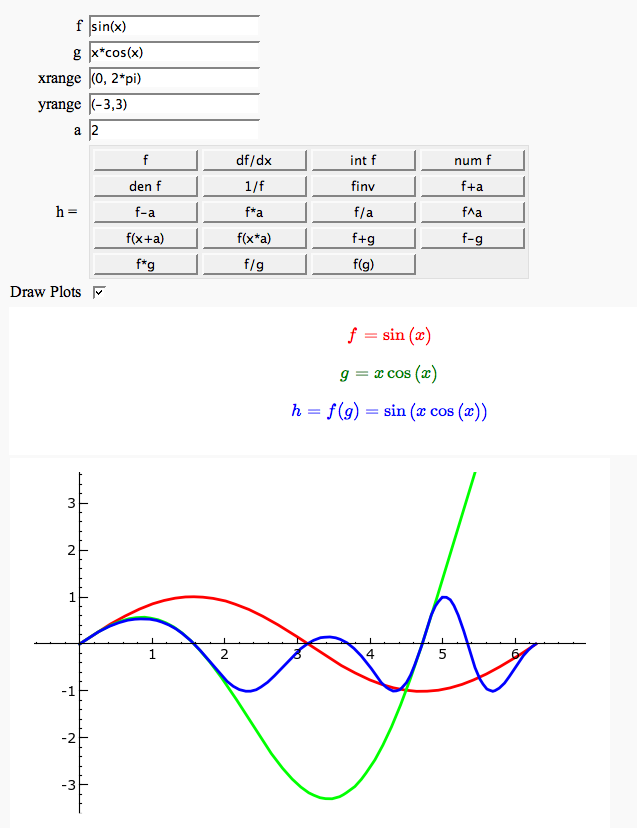
Newton-Raphson Root Finding
by Neal Holtz
This allows user to display the Newton-Raphson procedure one step at a time. It uses the heuristic that, if any of the values of the controls change, then the procedure should be re-started, else it should be continued.
# ideas from 'A simple tangent line grapher' by Marshall Hampton
# http://wiki.sagemath.org/interact
State = Data = None # globals to allow incremental changes in interaction data
@interact
def newtraph(f = input_box(default=8*sin(x)*exp(-x)-1, label='f(x)'),
xmin = input_box(default=0),
xmax = input_box(default=4*pi),
x0 = input_box(default=3, label='x0'),
show_calcs = ("Show Calcs",True),
step = ['Next','Prev', 'Reset'] ):
global State, Data
state = [f,xmin,xmax,x0,show_calcs]
if (state != State) or (step == 'Reset'): # when any of the controls change
Data = [ 1 ] # reset the plot
State = state
elif step == 'Next':
N, = Data
Data = [ N+1 ]
elif step == 'Prev':
N, = Data
if N > 1:
Data = [ N-1 ]
N, = Data
df = diff(f)
theplot = plot( f, xmin, xmax )
theplot += text( '\n$x_0$', (x0,0), rgbcolor=(1,0,0),
vertical_alignment="bottom" if f(x0) < 0 else "top" )
theplot += points( [(x0,0)], rgbcolor=(1,0,0) )
Trace = []
def Err( msg, Trace=Trace ):
Trace.append( '<font color="red"><b>Error: %s!!</b></font>' % (msg,) )
def Disp( s, color="blue", Trace=Trace ):
Trace.append( """<font color="%s">$ %s $</font>""" % (color,s,) )
Disp( """f(x) = %s""" % (latex(f),) )
Disp( """f'(x) = %s""" % (latex(df),) )
stop = False
is_inf = False
xi = x0
for i in range(N):
fi = RR(f(xi))
fpi = RR(df(xi))
theplot += points( [(xi,fi)], rgbcolor=(1,0,0) )
theplot += line( [(xi,0),(xi,fi)], linestyle=':', rgbcolor=(1,0,0) ) # vert dotted line
Disp( """i = %d""" % (i,) )
Disp( """~~~~x_{%d} = %.4g""" % (i,xi) )
Disp( """~~~~f(x_{%d}) = %.4g""" % (i,fi) )
Disp( """~~~~f'(x_{%d}) = %.4g""" % (i,fpi) )
if fpi == 0.0:
Err( 'Derivative is 0 at iteration %d' % (i+1,) )
is_inf = True
show_calcs = True
else:
xip1 = xi - fi/fpi
Disp( r"""~~~~x_{%d} = %.4g - ({%.4g})/({%.4g}) = %.4g""" % (i+1,xi,fi,fpi,xip1) )
if abs(xip1) > 10*(xmax-xmin):
Err( 'Derivative is too close to 0!' )
is_inf = True
show_calcs = True
elif not ((xmin - 0.5*(xmax-xmin)) <= xip1 <= (xmax + 0.5*(xmax-xmin))):
Err( 'x value out of range; probable divergence!' )
stop = True
show_calcs = True
if is_inf:
xl = xi - 0.05*(xmax-xmin)
xr = xi + 0.05*(xmax-xmin)
yl = yr = fi
else:
xl = min(xi,xip1) - 0.01*(xmax-xmin)
xr = max(xi,xip1) + 0.01*(xmax-xmin)
yl = -(xip1-xl)*fpi
yr = (xr-xip1)*fpi
theplot += text( '\n$x_{%d}$' % (i+1,), (xip1,0), rgbcolor=(1,0,0),
vertical_alignment="bottom" if f(xip1) < 0 else "top" )
theplot += points( [(xip1,0)], rgbcolor=(1,0,0) )
theplot += line( [(xl,yl),(xr,yr)], rgbcolor=(1,0,0) ) # tangent
if stop or is_inf:
break
epsa = 100.0*abs((xip1-xi)/xip1)
nsf = 2 - log(2.0*epsa)/log(10.0)
Disp( r"""~~~~~~~~\epsilon_a = \left|(%.4g - %.4g)/%.4g\right|\times100\%% = %.4g \%%""" % (xip1,xi,xip1,epsa) )
Disp( r"""~~~~~~~~num.~sig.~fig. \approx %.2g""" % (nsf,) )
xi = xip1
show( theplot, xmin=xmin, xmax=xmax )
if show_calcs:
for t in Trace:
html( t )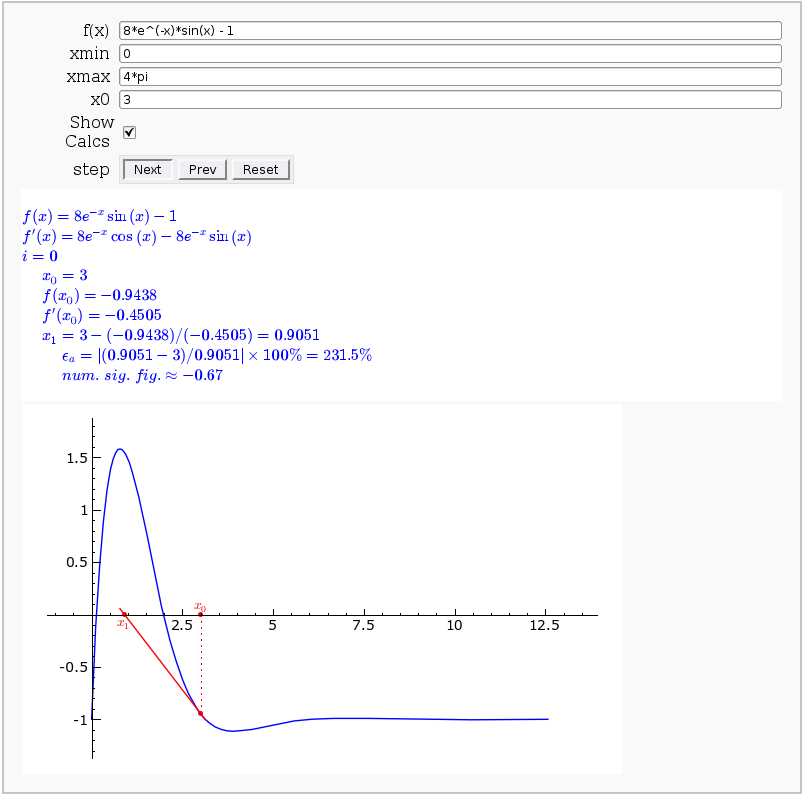
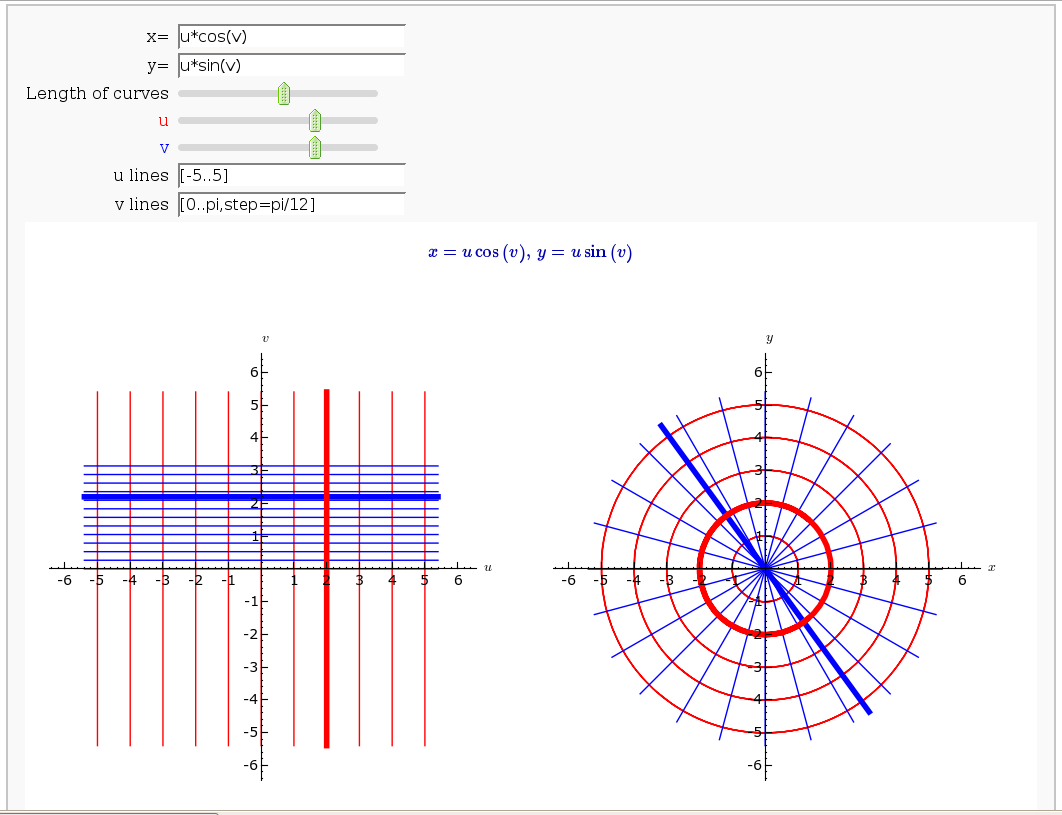
Coordinate Transformations
by Jason Grout
var('u v')
from sage.ext.fast_eval import fast_float
from functools import partial
@interact
def trans(x=input_box(u2-v2, label="x=",type=SR), \
y=input_box(u*v+cos(u*v), label="y=",type=SR), \
t_val=slider(0,10,0.2,6, label="Length of curves"), \
u_percent=slider(0,1,0.05,label="<font color='red'>u</font>", default=.7),
v_percent=slider(0,1,0.05,label="<font color='blue'>v</font>", default=.7),
u_range=input_box(range(-5,5,1), label="u lines"),
v_range=input_box(range(-5,5,1), label="v lines")):
thickness=4
u_val = min(u_range)+(max(u_range)-min(u_range))*u_percent
v_val = min(v_range)+(max(v_range)-min(v_range))*v_percent
t_min = -t_val
t_max = t_val
g1=sum([parametric_plot((i,v), t_min,t_max, rgbcolor=(1,0,0)) for i in u_range])
g2=sum([parametric_plot((u,i), t_min,t_max, rgbcolor=(0,0,1)) for i in v_range])
vline_straight=parametric_plot((u,v_val), t_min,t_max, rgbcolor=(0,0,1), linestyle='-',thickness=thickness)
uline_straight=parametric_plot((u_val, v), t_min,t_max,rgbcolor=(1,0,0), linestyle='-',thickness=thickness)
(g1+g2+vline_straight+uline_straight).save("uv_coord.png",aspect_ratio=1, figsize=[5,5], axes_labels=['$u$','$v$'])
xuv = fast_float(x,'u','v')
yuv = fast_float(y,'u','v')
xvu = fast_float(x,'v','u')
yvu = fast_float(y,'v','u')
g3=sum([parametric_plot((partial(xuv,i),partial(yuv,i)), t_min,t_max, rgbcolor=(1,0,0)) for i in u_range])
g4=sum([parametric_plot((partial(xvu,i),partial(yvu,i)), t_min,t_max, rgbcolor=(0,0,1)) for i in v_range])
vline=parametric_plot((partial(xvu,v_val),partial(yvu,v_val)), t_min,t_max, rgbcolor=(0,0,1), linestyle='-',thickness=thickness)
uline=parametric_plot((partial(xuv,u_val),partial(yuv,u_val)), t_min,t_max,rgbcolor=(1,0,0), linestyle='-',thickness=thickness)
(g3+g4+vline+uline).save("xy_coord.png", aspect_ratio=1, figsize=[5,5], axes_labels=['$x$','$y$'])
print jsmath("x=%s, \: y=%s"%(latex(x), latex(y)))
print "<html><table><tr><td><img src='cell://uv_coord.png'/></td><td><img src='cell://xy_coord.png'/></td></tr></table></html>"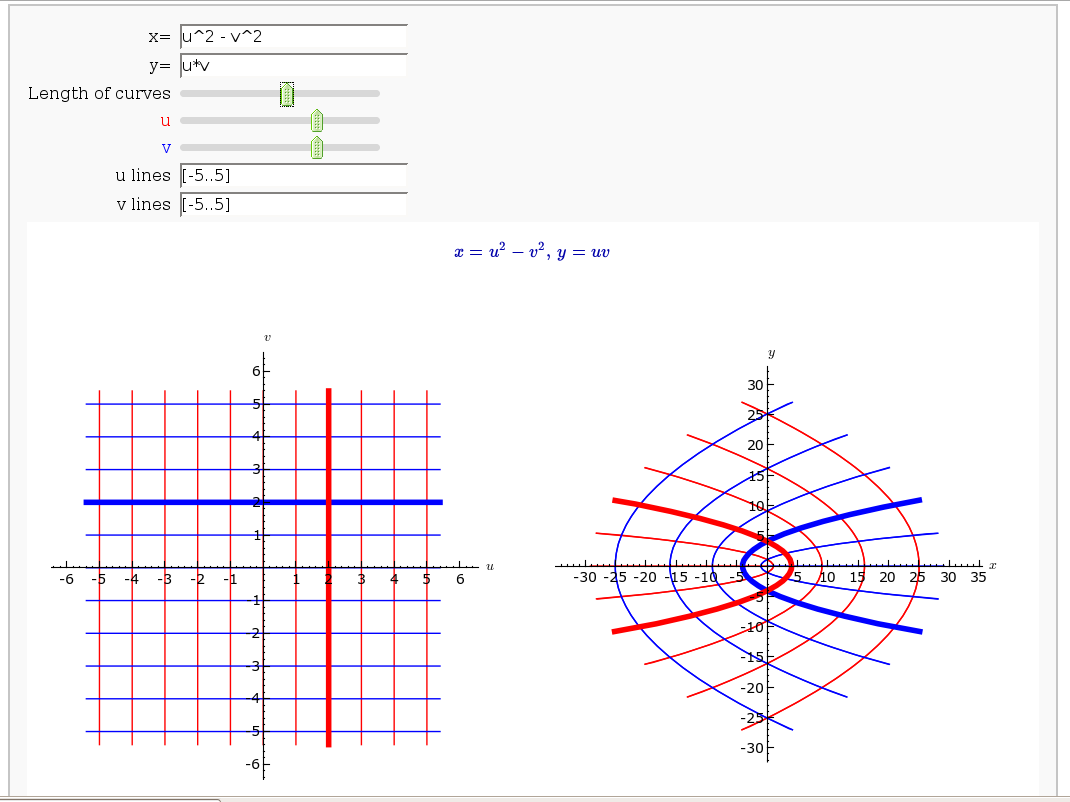
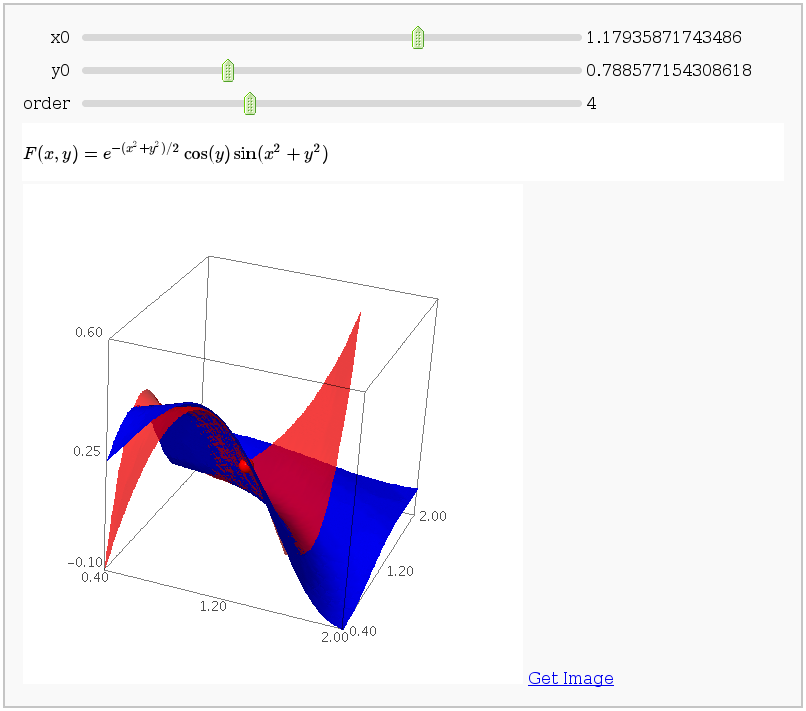
Taylor Series
by Harald Schilly
var('x')
x0 = 0
f = sin(x)*e^(-x)
p = plot(f,-1,5, thickness=2)
dot = point((x0,f(x0)),pointsize=80,rgbcolor=(1,0,0))
@interact
def _(order=(1..12)):
ft = f.taylor(x,x0,order)
pt = plot(ft,-1, 5, color='green', thickness=2)
html('$f(x)\;=\;%s$'%latex(f))
html('$\hat{f}(x;%s)\;=\;%s+\mathcal{O}(x^{%s})$'%(x0,latex(ft),order+1))
show(dot + p + pt, ymin = -.5, ymax = 1)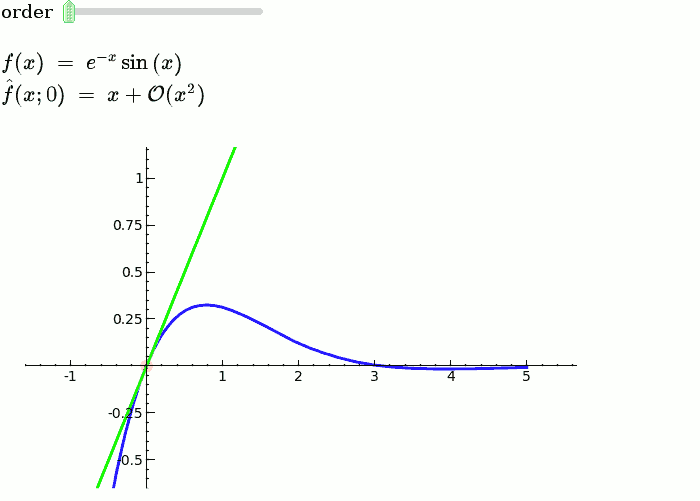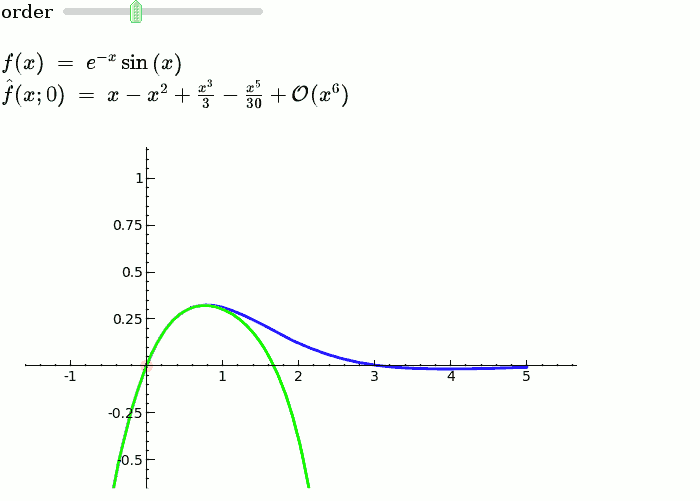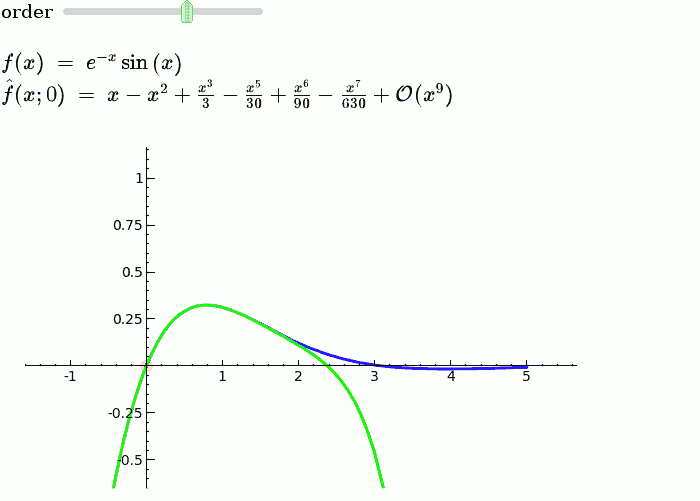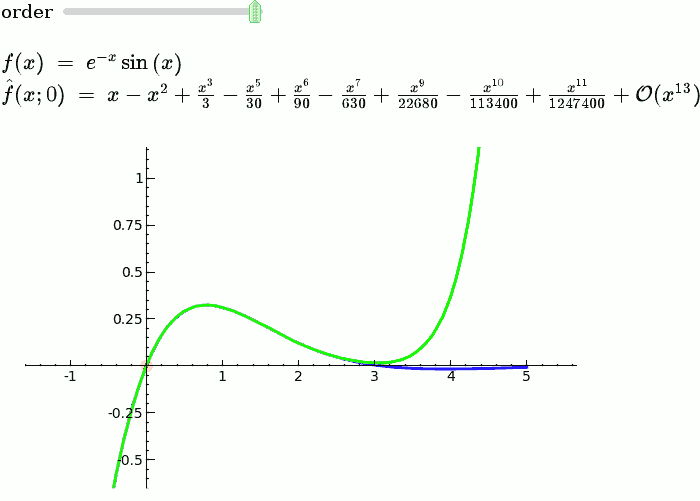
Illustration of the precise definition of a limit
by John Perry
I'll break tradition and put the image first. Apologies if this is Not A Good Thing.
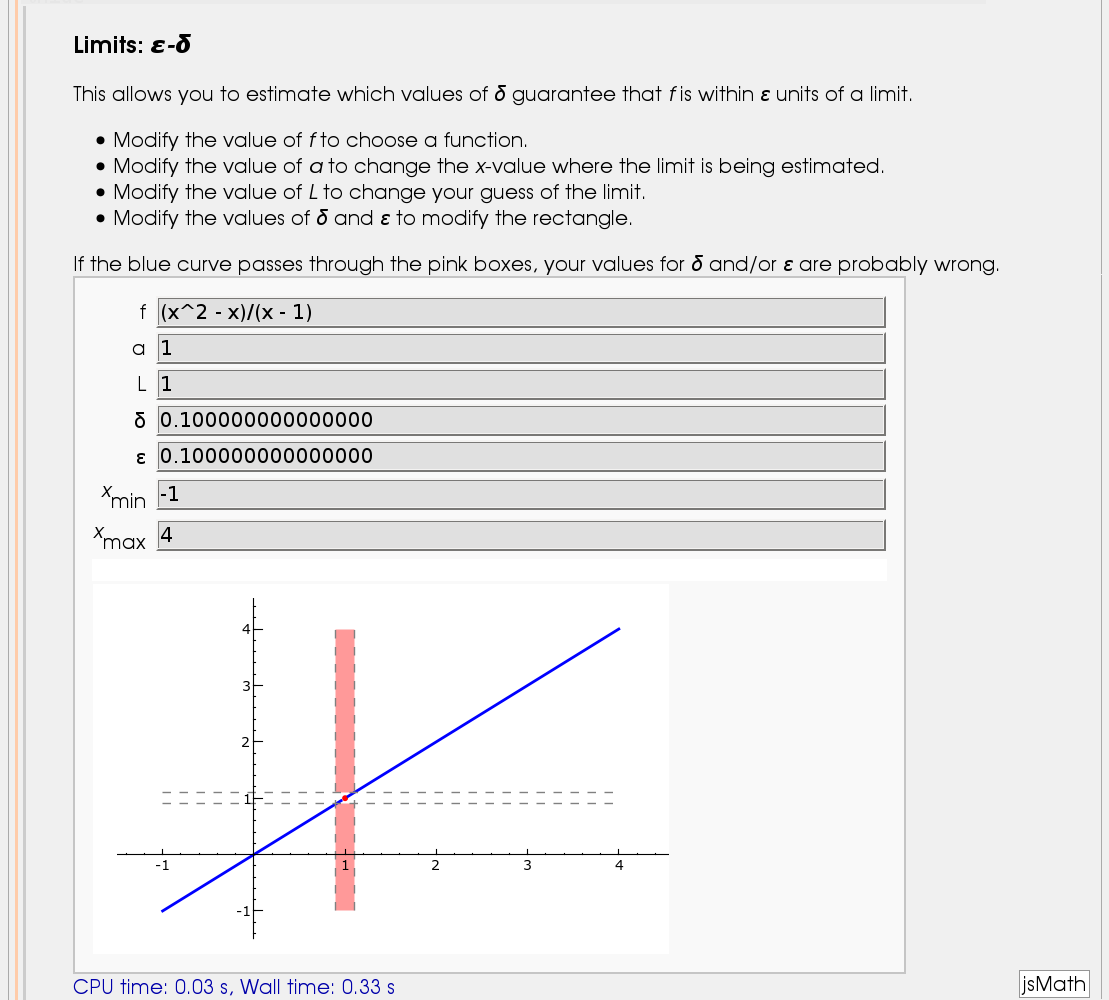
html("<h2>Limits: <i>ε-δ</i></h2>")
html("This allows you to estimate which values of <i>δ</i> guarantee that <i>f</i> is within <i>ε</i> units of a limit.")
html("<ul><li>Modify the value of <i>f</i> to choose a function.</li>")
html("<li>Modify the value of <i>a</i> to change the <i>x</i>-value where the limit is being estimated.</li>")
html("<li>Modify the value of <i>L</i> to change your guess of the limit.</li>")
html("<li>Modify the values of <i>δ</i> and <i>ε</i> to modify the rectangle.</li></ul>")
html("If the blue curve passes through the pink boxes, your values for <i>δ</i> and/or <i>ε</i> are probably wrong.")
@interact
def delta_epsilon(f = input_box(default=(x^2-x)/(x-1)), a=input_box(default=1), L = input_box(default=1), delta=input_box(label="δ",default=0.1), epsilon=input_box(label="ε",default=0.1), xm=input_box(label="<i>x</i><sub>min</sub>",default=-1), xM=input_box(label="<i>x</i><sub>max</sub>",default=4)):
f_left_plot = plot(f,xm,a-delta/3,thickness=2)
f_right_plot = plot(f,a+delta/3,xM,thickness=2)
epsilon_line_1 = line([(xm,L-epsilon),(xM,L-epsilon)], rgbcolor=(0.5,0.5,0.5),linestyle='--')
epsilon_line_2 = line([(xm,L+epsilon),(xM,L+epsilon)], rgbcolor=(0.5,0.5,0.5),linestyle='--')
ym = min(f_right_plot.ymin(),f_left_plot.ymin())
yM = max(f_right_plot.ymax(),f_left_plot.ymax())
bad_region_1 = polygon([(a-delta,L+epsilon),(a-delta,yM),(a+delta,yM),(a+delta,L+epsilon)], rgbcolor=(1,0.6,0.6))
bad_region_2 = polygon([(a-delta,L-epsilon),(a-delta,ym),(a+delta,ym),(a+delta,L-epsilon)], rgbcolor=(1,0.6,0.6))
aL_point = point((a,L),rgbcolor=(1,0,0),pointsize=20)
delta_line_1 = line([(a-delta,ym),(a-delta,yM)],rgbcolor=(0.5,0.5,0.5),linestyle='--')
delta_line_2 = line([(a+delta,ym),(a+delta,yM)],rgbcolor=(0.5,0.5,0.5),linestyle='--')
(f_left_plot +f_right_plot +epsilon_line_1 +epsilon_line_2 +delta_line_1 +delta_line_2 +aL_point +bad_region_1 +bad_region_2).show(xmin=xm,xmax=xM)
A graphical illustration of sin(x)/x -> 1 as x-> 0
by Wai Yan Pong
x=var('x')
@interact
def _(x = slider(-7/10,7/10,1/20,1/2)):
html('<h3>A graphical illustration of $\lim_{x -> 0} \sin(x)/x =1$</h3>')
html('Below is the unit circle, so the length of the <font color=red>red line</font> is |sin(x)|')
html('and the length of the <font color=blue>blue line</font> is |tan(x)| where x is the length of the arc.')
html('From the picture, we see that |sin(x)| $\le$ |x| $\le$ |tan(x)|.')
html('It follows easily from this that cos(x) $\le$ sin(x)/x $\le$ 1 when x is near 0.')
html('As $\lim_{x ->0} \cos(x) =1$, we conclude that $\lim_{x -> 0} \sin(x)/x =1$.')
if not (x == 0):
pretty_print("sin(x)/x = "+str(sin(float(x))/float(x)))
elif x == 0:
pretty_print("The limit of sin(x)/x as x tends to 0 is 1.")
C=circle((0,0),1, rgbcolor='black')
mvp = (cos(x),sin(x));tpt = (1, tan(x))
p1 = point(mvp, pointsize=30, rgbcolor='red'); p2 = point((1,0), pointsize=30, rgbcolor='red')
line1 = line([(0,0),tpt], rgbcolor='black'); line2 = line([(cos(x),0),mvp], rgbcolor='red')
line3 = line([(0,0),(1,0)], rgbcolor='black'); line4 = line([(1,0),tpt], rgbcolor='blue')
result = C+p1+p2+line1+line2+line3+line4
result.show(aspect_ratio=1, figsize=[3,3], axes=False)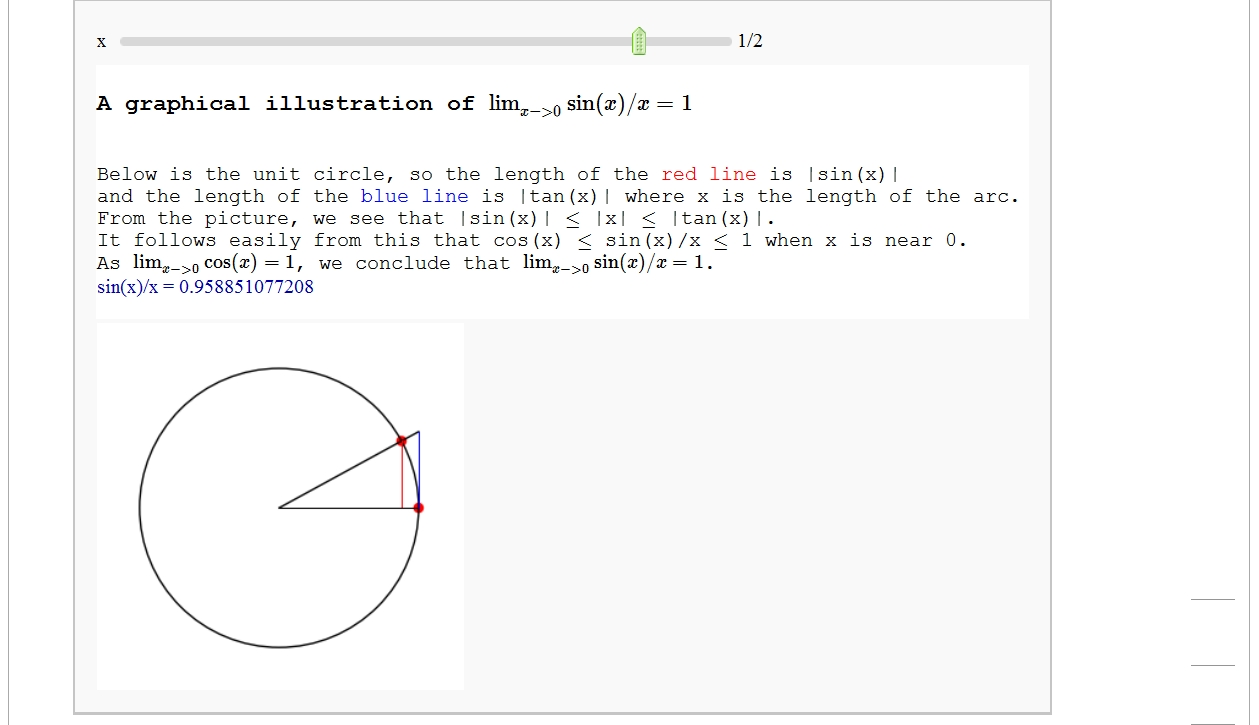
Quadric Surface Plotter
by Marshall Hampton. This is pretty simple, so I encourage people to spruce it up. In particular, it isn't set up to show all possible types of quadrics.
var('x,y,z')
quadrics = {'Ellipsoid':x^2+y^2+z^2-1,'Elliptic paraboloid':x^2+y^2-z,'Hyperbolic paraboloid':x^2-y^2-z, '1-Sheeted Hyperboloid':x^2+y^2-z^2-1,'2-Sheeted Hyperboloid':x^2-y^2-z^2-1, 'Cone':x^2+y^2-z^2}
@interact
def quads(q = selector(quadrics.keys()), a = slider(0,5,1/2,default = 1)):
f = quadrics[q].subs({x:x*a^(1/2)})
if a==0 or q=='Cone': html('<center>$'+latex(f)+' \ $'+ '(degenerate)</center>')
else: html('<center>$'+latex(f)+'$ </center>')
p = implicit_plot3d(f,(x,-2,2),(y,-2,2),(z,-2,2), plot_points = 75)
show(p)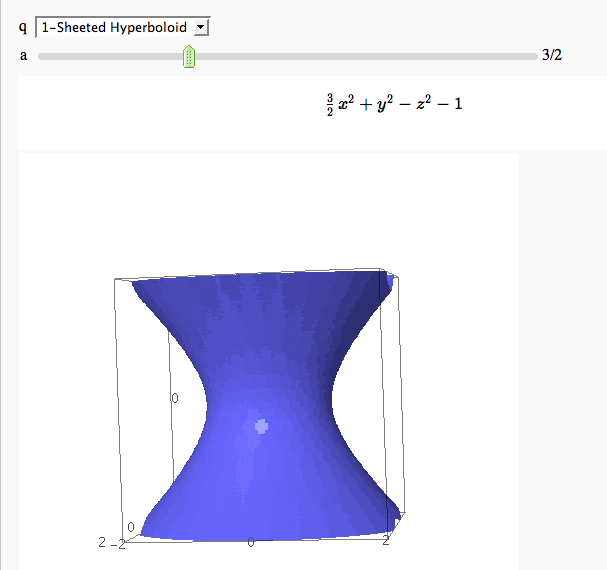
The midpoint rule for numerically integrating a function of two variables
by Marshall Hampton
from sage.plot.plot3d.platonic import index_face_set
def cuboid(v1,v2,**kwds):
"""
Cuboid defined by corner points v1 and v2.
"""
ptlist = []
for vi in (v1,v2):
for vj in (v1,v2):
for vk in (v1,v2):
ptlist.append([vi[0],vj[1],vk[2]])
f_incs = [[0, 2, 6, 4], [0, 1, 3, 2], [0, 1, 5, 4], [1, 3, 7, 5], [2, 3, 7, 6], [4, 5, 7, 6]]
if 'aspect_ratio' not in kwds:
kwds['aspect_ratio'] = [1,1,1]
return index_face_set(f_incs,ptlist,enclosed = True, **kwds)
var('x,y')
R16 = RealField(16)
npi = RDF(pi)
sin,cos = math.sin,math.cos
html("<h1>The midpoint rule for a function of two variables</h1>")
@interact
def midpoint2d(func = input_box('y*sin(x)/x+sin(y)',type=str,label='function of x and y'), nx = slider(2,20,1,3,label='x subdivisions'), ny = slider(2,20,1,3,label='y subdivisions'), x_start = slider(-10,10,.1,0), x_end = slider(-10,10,.1,3*npi), y_start= slider(-10,10,.1,0), y_end= slider(-10,10,.1,3*npi)):
f = sage_eval('lambda x,y: ' + func)
delx = (x_end - x_start)/nx
dely = (y_end - y_start)/nx
xvals = [RDF(x_start + (i+1.0/2)*delx) for i in range(nx)]
yvals = [RDF(y_start + (i+1.0/2)*dely) for i in range(ny)]
num_approx = 0
cubs = []
darea = delx*dely
for xv in xvals:
for yv in yvals:
num_approx += f(xv,yv)*darea
cubs.append(cuboid([xv-delx/2,yv-dely/2,0],[xv+delx/2,yv+dely/2,f(xv,yv)], opacity = .5, rgbcolor = (1,0,0)))
html("$$\int_{"+str(R16(y_start))+"}^{"+str(R16(y_end))+"} "+ "\int_{"+str(R16(x_start))+"}^{"+str(R16(x_end))+"} "+func+"\ dx \ dy$$")
html('<p style="text-align: center;">Numerical approximation: ' + str(num_approx)+'</p>')
p1 = plot3d(f,(x,x_start,x_end),(y,y_start,y_end))
show(p1+sum(cubs))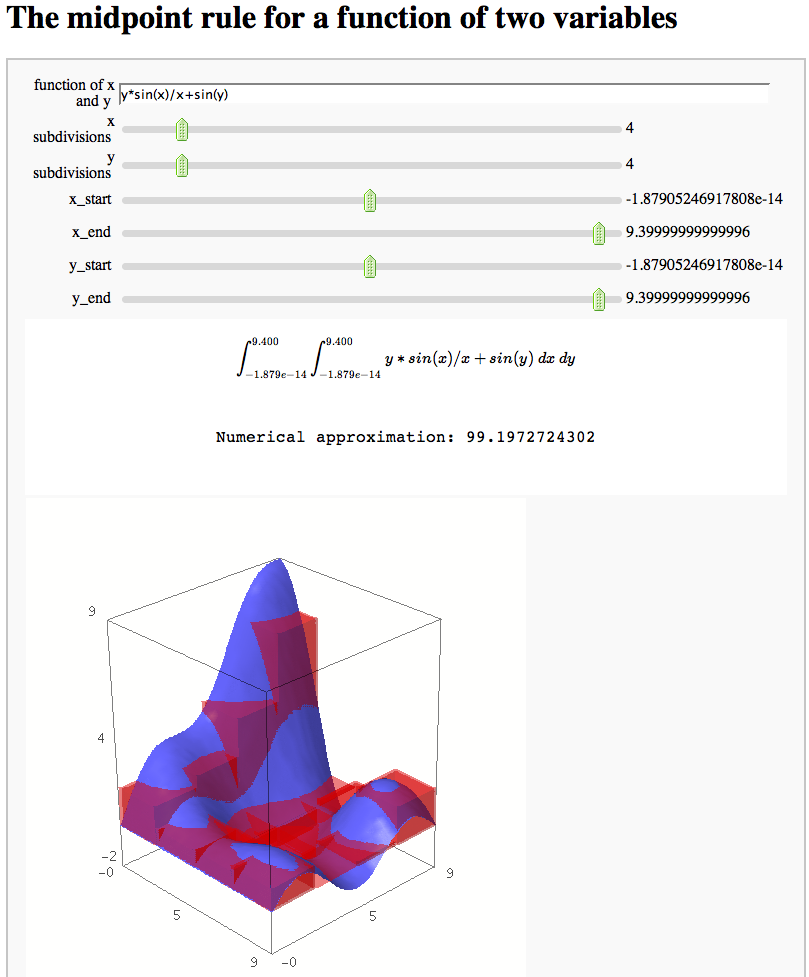
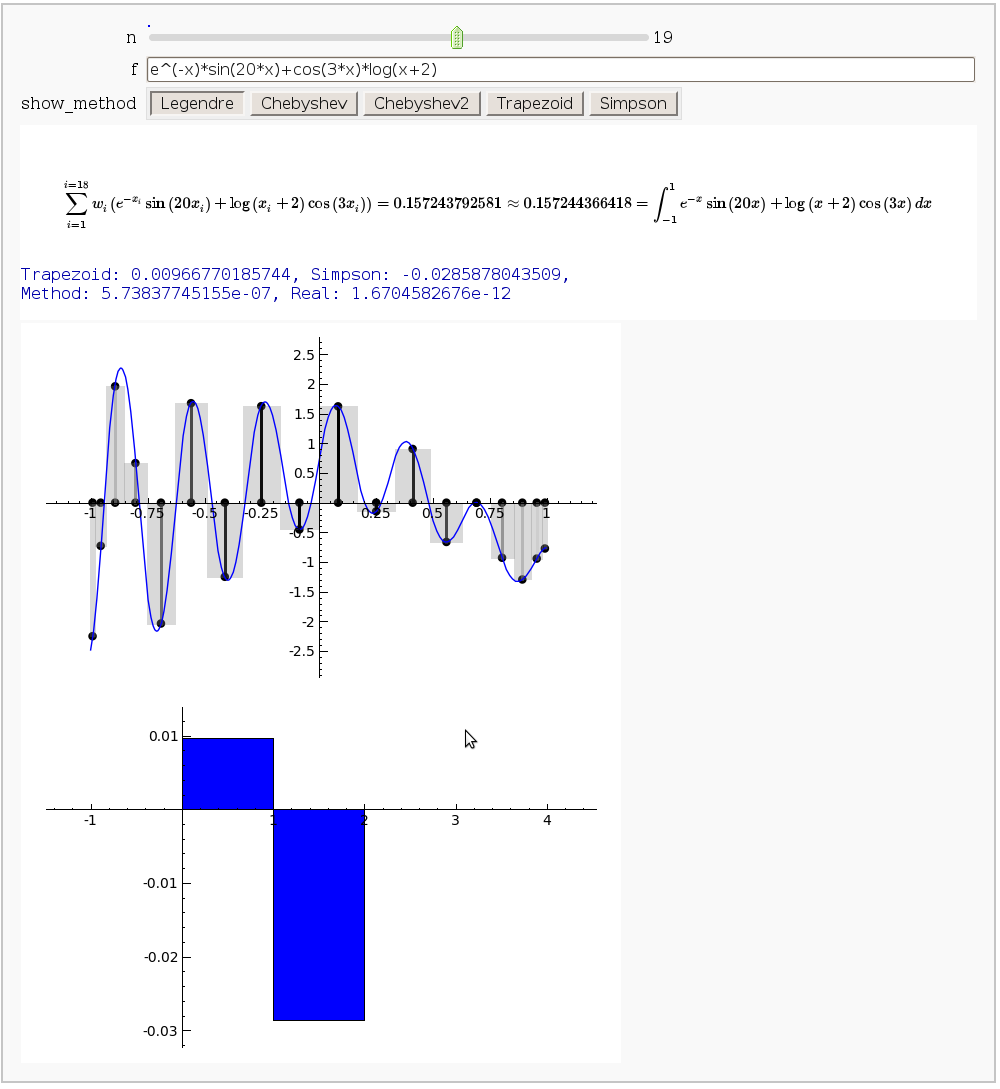
Gaussian (Legendre) quadrature
by Jason Grout
The output shows the points evaluated using Gaussian quadrature (using a weight of 1, so using Legendre polynomials). The vertical bars are shaded to represent the relative weights of the points (darker = more weight). The error in the trapezoid, Simpson, and quadrature methods is both printed out and compared through a bar graph. The "Real" error is the error returned from scipy on the definite integral.
from scipy.special.orthogonal import p_roots
from scipy.integrate import quad, trapz, simps
from sage.ext.fast_eval import fast_float
from numpy import linspace
show_weight_graph=False
# 'Hermite': {'w': e**(-x**2), 'xmin': -numpy.inf, 'xmax': numpy.inf, 'func': h_roots},
# 'Laguerre': {'w': e**(-x), 'xmin': 0, 'xmax': numpy.inf, 'func': l_roots},
methods = {'Legendre': {'w': 1, 'xmin': -1, 'xmax': 1, 'func': p_roots},
'Chebyshev': {'w': 1/sqrt(1-x**2), 'xmin': -1, 'xmax': 1, 'func': t_roots},
'Chebyshev2': {'w': sqrt(1-x**2), 'xmin': -1, 'xmax': 1, 'func': u_roots},
'Trapezoid': {'w': 1, 'xmin': -1, 'xmax': 1, 'func': lambda n: (linspace(-1r,1,n), numpy.array([1.0r]+[2.0r]*(n-2)+[1.0r])*1.0r/n)},
'Simpson': {'w': 1, 'xmin': -1, 'xmax': 1, 'func': lambda n: (linspace(-1r,1,n), numpy.array([1.0r]+[4.0r,2.0r]*int((n-3.0r)/2.0r)+[4.0r,1.0r])*2.0r/(3.0r*n))}}
var("x")
def box(center, height, area,**kwds):
width2 = 1.0*area/height/2.0
return polygon([(center-width2,0),(center+width2,0),(center+width2,height),(center-width2,height)],**kwds)
@interact
def weights(n=slider(1,30,1,default=10),f=input_box(default=3*x+cos(10*x)),show_method=["Legendre", "Chebyshev", "Chebyshev2", "Trapezoid","Simpson"]):
ff = fast_float(f,'x')
method = methods[show_method]
xcoords,w = (method['func'])(int(n))
xmin = method['xmin']
xmax = method['xmax']
plot_min = max(xmin, -10)
plot_max = min(xmax, 10)
scaled_func = f*method['w']
scaled_ff = fast_float(scaled_func)
coords = zip(xcoords,w)
max_weight = max(w)
coords_scaled = zip(xcoords,w/max_weight)
f_graph = plot(scaled_func,plot_min,plot_max)
boxes = sum(box(x,ff(x),w*ff(x),rgbcolor=(0.5,0.5,0.5),alpha=0.3) for x,w in coords)
stems = sum(line([(x,0),(x,scaled_ff(x))],rgbcolor=(1-y,1-y,1-y),thickness=2,markersize=6,alpha=y) for x,y in coords_scaled)
points = sum([point([(x,0),(x,scaled_ff(x))],rgbcolor='black',pointsize=30) for x,_ in coords])
graph = stems+points+f_graph+boxes
if show_weight_graph:
graph += line([(x,y) for x,y in coords_scaled], rgbcolor='green',alpha=0.4)
show(graph,xmin=plot_min,xmax=plot_max)
approximation = sum([w*ff(x) for x,w in coords])
integral,integral_error = scipy.integrate.quad(scaled_ff, xmin, xmax)
x_val = linspace(min(xcoords), max(xcoords),n)
y_val = map(scaled_ff,x_val)
trapezoid = integral-trapz(y_val, x_val)
simpson = integral-simps(y_val, x_val)
html("$$\sum_{i=1}^{i=%s}w_i\left(%s\\right)= %s\\approx %s =\int_{-1}^{1}%s \,dx$$"%(n,latex(f.subs(x="x_i")), approximation, integral, latex(scaled_func)))
error_data = [trapezoid, simpson, integral-approximation,integral_error]
print "Trapezoid: %s, Simpson: %s, \nMethod: %s, Real: %s"%tuple(error_data)
show(bar_chart(error_data,width=1),ymin=min(error_data), ymax=max(error_data))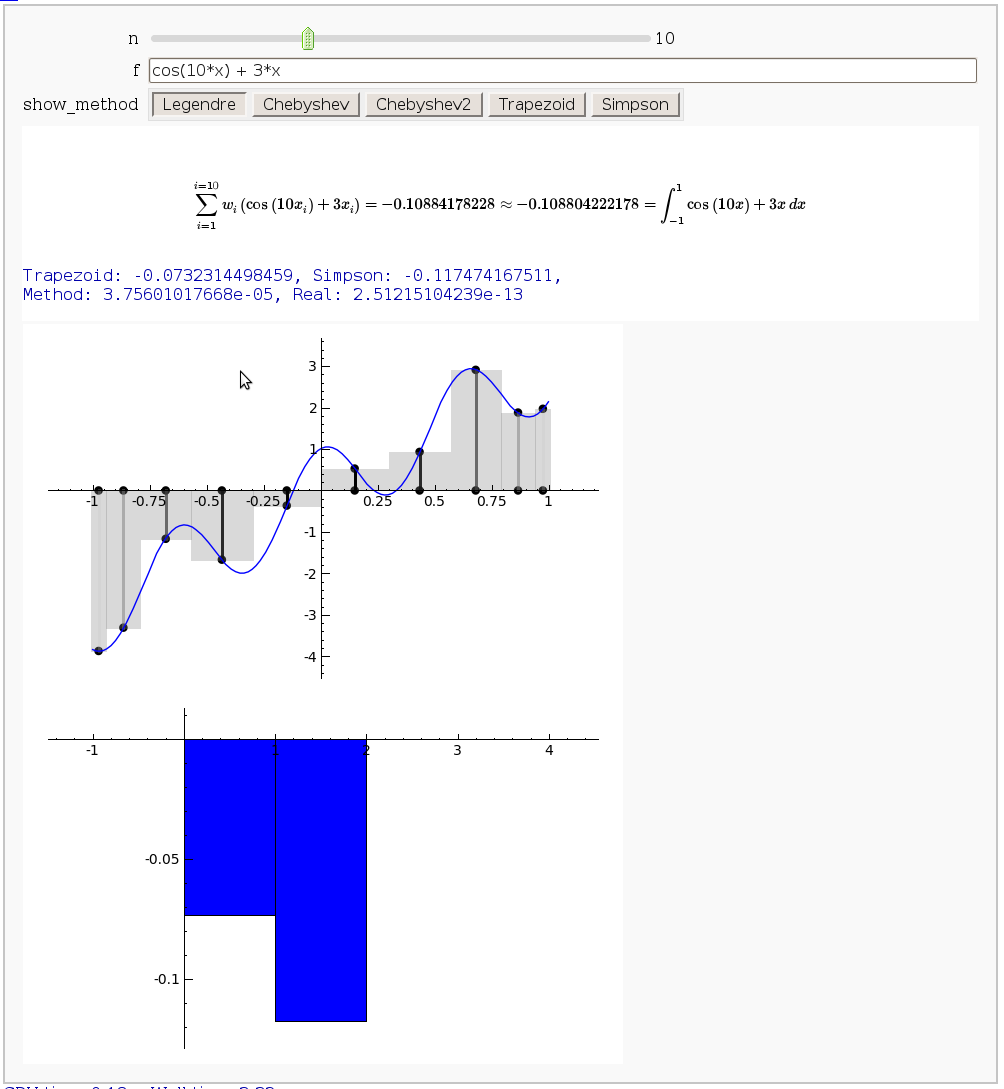
Vector Calculus, 2-D Motion
By Rob Beezer
A fast_float() version is available in a worksheet
# 2-D motion and vector calculus
# Copyright 2009, Robert A. Beezer
# Creative Commons BY-SA 3.0 US
#
# 2009/02/15 Built on Sage 3.3.rc0
# 2009/02/17 Improvements from Jason Grout
#
# variable parameter is t
# later at a particular value named t0
#
var('t')
#
# parameter range
#
start=0
stop=2*pi
#
# position vector definition
# edit here for new example
# example is wide ellipse
# adjust x, extents in final show()
#
position=vector( (4*cos(t), sin(t)) )
#
# graphic of the motion itself
#
path = parametric_plot( position(t).list(), (t, start, stop), color = "black" )
#
# derivatives of motion, lengths, unit vectors, etc
#
velocity = derivative( position(t) )
acceleration = derivative(velocity(t))
speed = velocity.norm()
speed_deriv = derivative(speed)
tangent = (1/speed)*velocity
dT = derivative(tangent(t))
normal = (1/dT.norm())*dT
#
# interact section
# slider for parameter, 24 settings
# checkboxes for various vector displays
# computations at one value of parameter, t0
#
@interact
def _(t0 = slider(float(start), float(stop), float((stop-start)/24), float(start) , label = "Parameter"),
pos_check = ("Position", True),
vel_check = ("Velocity", False),
tan_check = ("Unit Tangent", False),
nor_check = ("Unit Normal", False),
acc_check = ("Acceleration", False),
tancomp_check = ("Tangential Component", False),
norcomp_check = ("Normal Component", False)
):
#
# location of interest
#
pos_tzero = position(t0)
#
# various scalar quantities at point
#
speed_component = speed(t0)
tangent_component = speed_deriv(t0)
normal_component = sqrt( acceleration(t0).norm()^2 - tangent_component^2 )
curvature = normal_component/speed_component^2
#
# various vectors, mostly as arrows from the point
#
pos = arrow((0,0), pos_tzero, rgbcolor=(0,0,0))
tan = arrow(pos_tzero, pos_tzero + tangent(t0), rgbcolor=(0,1,0) )
vel = arrow(pos_tzero, pos_tzero + velocity(t0), rgbcolor=(0,0.5,0))
nor = arrow(pos_tzero, pos_tzero + normal(t0), rgbcolor=(0.5,0,0))
acc = arrow(pos_tzero, pos_tzero + acceleration(t0), rgbcolor=(1,0,1))
tancomp = arrow(pos_tzero, pos_tzero + tangent_component*tangent(t0), rgbcolor=(1,0,1) )
norcomp = arrow(pos_tzero, pos_tzero + normal_component*normal(t0), rgbcolor=(1,0,1))
#
# accumulate the graphic based on checkboxes
#
picture = path
if pos_check:
picture = picture + pos
if vel_check:
picture = picture + vel
if tan_check:
picture = picture+ tan
if nor_check:
picture = picture + nor
if acc_check:
picture = picture + acc
if tancomp_check:
picture = picture + tancomp
if norcomp_check:
picture = picture + norcomp
#
# print textual info
#
print "Position vector defined as r(t)=", position(t)
print "Speed is ", N(speed(t0))
print "Curvature is ", N(curvature)
#
# show accumulated graphical info
# adjust x-,y- extents to get best plot
#
show(picture, xmin=-4,xmax=4, ymin=-1.5,ymax=1.5,aspect_ratio=1)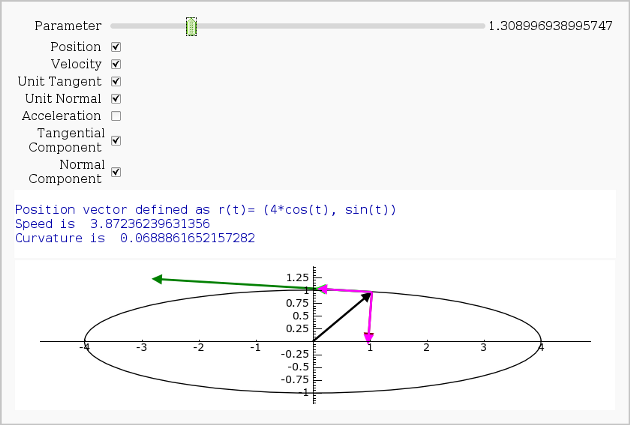
Vector Calculus, 3-D Motion
by Rob Beezer
Available as a worksheet
# 3-D motion and vector calculus
# Copyright 2009, Robert A. Beezer
# Creative Commons BY-SA 3.0 US
#
#
# 2009/02/15 Built on Sage 3.3.rc0
# 2009/02/17 Improvements from Jason Grout
#
# variable parameter is t
# later at a particular value named t0
#
# un-comment double hash (##) to get
# time-consuming torsion computation
#
var('t')
#
# parameter range
#
start=-4*pi
stop=8*pi
#
# position vector definition
# edit here for new example
# example is wide ellipse
# adjust figsize in final show() to get accurate aspect ratio
#
a=1/(8*pi)
c=(3/2)*a
position=vector( (exp(a*t)*cos(t), exp(a*t)*sin(t), exp(c*t)) )
#
# graphic of the motion itself
#
path = parametric_plot3d( position(t).list(), (t, start, stop), color = "black" )
#
# derivatives of motion, lengths, unit vectors, etc
#
velocity = derivative( position(t) )
acceleration = derivative(velocity(t))
speed = velocity.norm()
speed_deriv = derivative(speed)
tangent = (1/speed)*velocity
dT = derivative(tangent(t))
normal = (1/dT.norm())*dT
binormal = tangent.cross_product(normal)
## dB = derivative(binormal(t))
#
# interact section
# slider for parameter, 24 settings
# checkboxes for various vector displays
# computations at one value of parameter, t0
#
@interact
def _(t0 = slider(float(start), float(stop), float((stop-start)/24), float(start) , label = "Parameter"),
pos_check = ("Position", True),
vel_check = ("Velocity", False),
tan_check = ("Unit Tangent", False),
nor_check = ("Unit Normal", False),
bin_check = ("Unit Binormal", False),
acc_check = ("Acceleration", False),
tancomp_check = ("Tangential Component", False),
norcomp_check = ("Normal Component", False)
):
#
# location of interest
#
pos_tzero = position(t0)
#
# various scalar quantities at point
#
speed_component = speed(t0)
tangent_component = speed_deriv(t0)
normal_component = sqrt( acceleration(t0).norm()^2 - tangent_component^2 )
curvature = normal_component/speed_component^2
## torsion = (1/speed_component)*(dB(t0)).dot_product(normal(t0))
#
# various vectors, mostly as arrows from the point
#
pos = arrow3d((0,0,0), pos_tzero, rgbcolor=(0,0,0))
tan = arrow3d(pos_tzero, pos_tzero + tangent(t0), rgbcolor=(0,1,0) )
vel = arrow3d(pos_tzero, pos_tzero + velocity(t0), rgbcolor=(0,0.5,0))
nor = arrow3d(pos_tzero, pos_tzero + normal(t0), rgbcolor=(0.5,0,0))
bin = arrow3d(pos_tzero, pos_tzero + binormal(t0), rgbcolor=(0,0,0.5))
acc = arrow3d(pos_tzero, pos_tzero + acceleration(t0), rgbcolor=(1,0,1))
tancomp = arrow3d(pos_tzero, pos_tzero + tangent_component*tangent(t0), rgbcolor=(1,0,1) )
norcomp = arrow3d(pos_tzero, pos_tzero + normal_component*normal(t0), rgbcolor=(1,0,1))
#
# accumulate the graphic based on checkboxes
#
picture = path
if pos_check:
picture = picture + pos
if vel_check:
picture = picture + vel
if tan_check:
picture = picture+ tan
if nor_check:
picture = picture + nor
if bin_check:
picture = picture + bin
if acc_check:
picture = picture + acc
if tancomp_check:
picture = picture + tancomp
if norcomp_check:
picture = picture + norcomp
#
# print textual info
#
print "Position vector: r(t)=", position(t)
print "Speed is ", N(speed(t0))
print "Curvature is ", N(curvature)
## print "Torsion is ", N(torsion)
print
print "Right-click on graphic to zoom to 400%"
print "Drag graphic to rotate"
#
# show accumulated graphical info
#
show(picture, aspect_ratio=[1,1,1])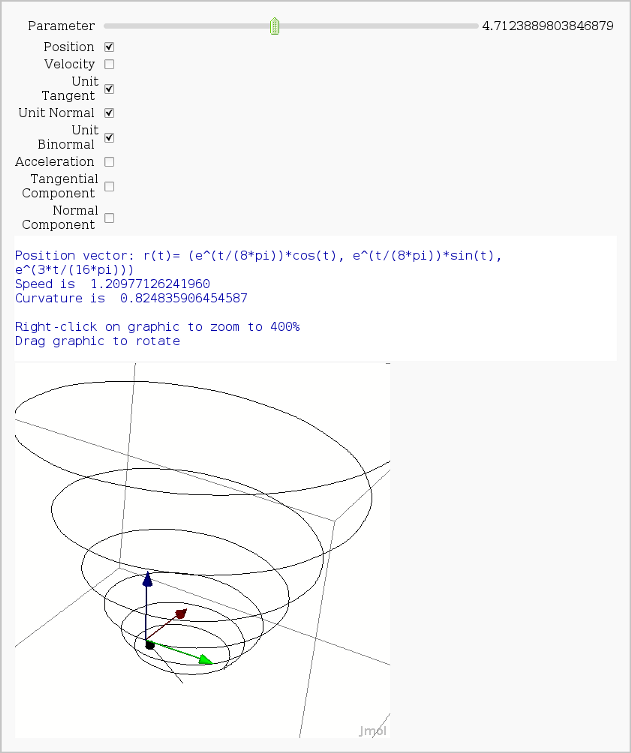
Directional Derivatives
This interact displays graphically a tangent line to a function, illustrating a directional derivative (the slope of the tangent line).
var('x,y,t,z')
f(x,y)=sin(x)*cos(y)
pif = float(pi)
line_thickness=3
surface_color='blue'
plane_color='purple'
line_color='red'
tangent_color='green'
gradient_color='orange'
@interact
def myfun(location=input_grid(1, 2, default=[0,0], label = "Location (x,y)", width=2), angle=slider(0, 2*pif, label = "Angle"),
show_surface=("Show surface", True)):
location3d = vector(location[0]+[0])
location = location3d[0:2]
direction3d = vector(RDF, [cos(angle), sin(angle), 0])
direction=direction3d[0:2]
cos_angle = math.cos(angle)
sin_angle = math.sin(angle)
df = f.gradient()
direction_vector=line3d([location3d, location3d+direction3d], arrow_head=True, rgbcolor=line_color, thickness=line_thickness)
curve_point = (location+t*direction).list()
curve = parametric_plot(curve_point+[f(*curve_point)], (t,-3,3),color=line_color,thickness=line_thickness)
plane = parametric_plot((cos_angle*x+location[0],sin_angle*x+location[1],t), (x, -3,3), (t,-3,3),opacity=0.8, color=plane_color)
pt = point3d(location3d.list(),color='green', size=10)
tangent_line = parametric_plot((location[0]+t*cos_angle, location[1]+t*sin_angle, f(*location)+t*df(*location)*(direction)), (t, -3,3), thickness=line_thickness, color=tangent_color)
picture3d = direction_vector+curve+plane+pt+tangent_line
picture2d = contour_plot(f(x,y), (x,-3,3),(y,-3,3), plot_points=100)
picture2d += arrow(location.list(), (location+direction).list())
picture2d += point(location.list(),rgbcolor='green',pointsize=40)
if show_surface:
picture3d += plot3d(f, (x,-3,3),(y,-3,3),opacity=0.7)
dff = df(location[0], location[1])
dff3d = vector(RDF,dff.list()+[0])
picture3d += line3d([location3d, location3d+dff3d], arrow_head=True, rgbcolor=gradient_color, thickness=line_thickness)
picture2d += arrow(location.list(), (location+dff).list(), rgbcolor=gradient_color, width=line_thickness)
show(picture3d,aspect=[1,1,1], axes=True)
show(picture2d, aspect_ratio=1)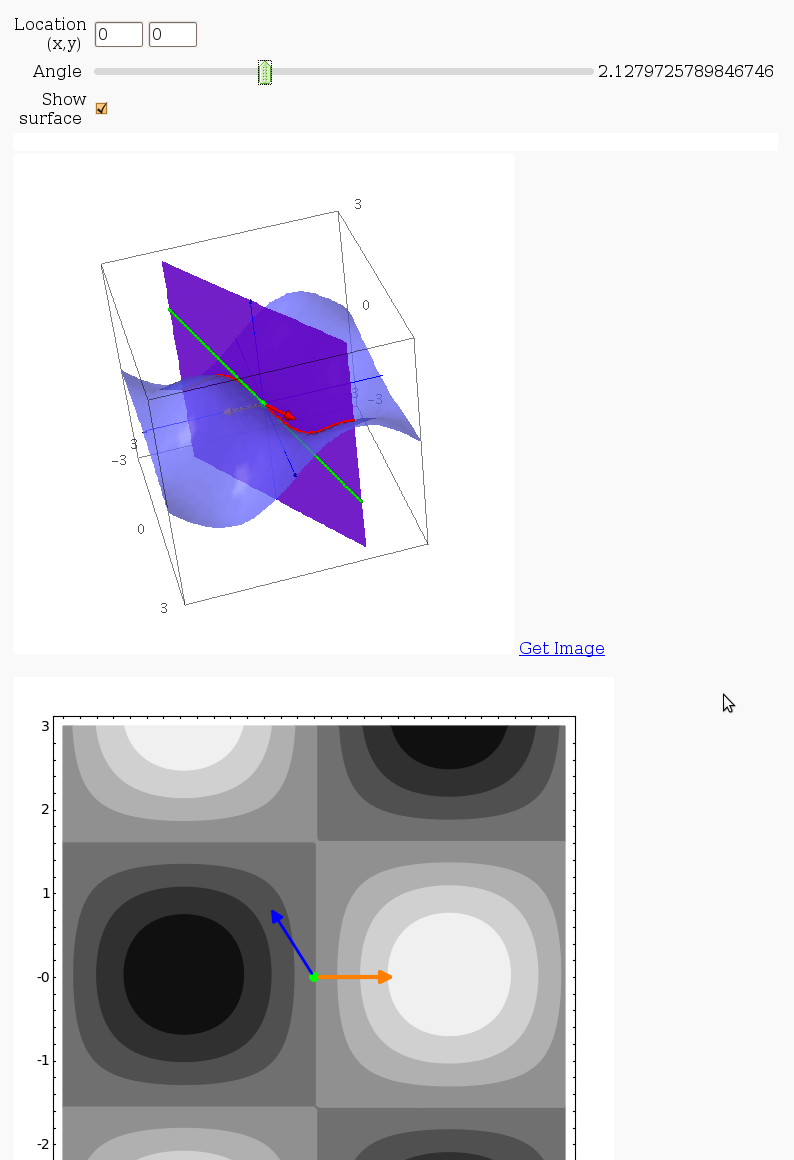
3D graph with points and curves
By Robert Marik
This sagelet is handy when showing local, constrained and absolute maxima and minima in two variables. Available as a worksheet
%hide
%auto
x,y, t, u, v =var('x y t u v')
INI_func='x^2-2*x+y^2-2*y'
INI_box='-1,3.2,-1,3.2'
INI_points='(1,1,\'green\'),(3/2,3/2),(0,1),(1,0),(0,0,\'black\'),(3,0,\'black\'),(0,3,\'black\')'
INI_curves='(t,0,0,3,\'red\'),(0,t,0,3,\'green\'),(t,3-t,0,3)'
@interact
def _(func=input_box(INI_func,label="f(x,y)=",type=str),\
bounds=input_box(INI_box,label="xmin,xmax,ymin,ymax",type=str),\
st_points=input_box(INI_points,\
label="points <br><small><small>(comma separated pairs, optionally with color)</small></small>", type=str),\
bnd_curves=input_box(INI_curves,label="curves on boundary<br> <small><small><i>(x(t),y(t),tmin,tmax,'opt_color')</i></small></small>", type=str),\
show_planes=("Show zero planes", False), show_axes=("Show axes", True),
show_table=("Show table", True)):
f=sage_eval('lambda x,y: ' + func)
html(r'Function $ f(x,y)=%s$ '%latex(f(x,y)))
xmin,xmax,ymin,ymax=sage_eval('('+bounds+')')
A=plot3d(f(x,y),(x,xmin,xmax),(y,ymin,ymax),opacity=0.5)
if not(bool(st_points=='')):
st_p=sage_eval('('+st_points+',)')
html(r'<table border=1>')
for current in range(len(st_p)):
point_color='red'
if bool(len(st_p[current])==3):
point_color=st_p[current][2]
x0=st_p[current][0]
y0=st_p[current][1]
z0=f(x0,y0)
if show_table:
html(r'<tr><td>$\quad f(%s,%s)\quad $</td><td>$\quad %s$</td>\
</tr>'%(latex(x0),latex(y0),z0.n()))
A=A+point3d((x0,y0,z0),size=9,rgbcolor=point_color)
html(r'</table>')
if not(bool(bnd_curves=='')):
bnd_cc=sage_eval('('+bnd_curves+',)',locals={'t':t})
for current in range(len(bnd_cc)):
bnd_c=bnd_cc[current]+('black',)
A=A+parametric_plot3d((bnd_c[0],bnd_c[1],f(bnd_c[0],bnd_c[1])),\
(t,bnd_c[2],bnd_c[3]),thickness=3,rgbcolor=bnd_c[4])
if show_planes:
A=A+plot3d(0,(x,xmin,xmax),(y,ymin,ymax),opacity=0.3,rgbcolor='gray')
zmax=A.bounding_box()[1][2]
zmin=A.bounding_box()[0][2]
A=A+parametric_plot3d((u,0,v),(u,xmin,xmax),(v,zmin,zmax),opacity=0.3,rgbcolor='gray')
A=A+parametric_plot3d((0,u,v),(u,ymin,ymax),(v,zmin,zmax),opacity=0.3,rgbcolor='gray')
if show_axes:
zmax=A.bounding_box()[1][2]
zmin=A.bounding_box()[0][2]
A=A+line3d([(xmin,0,0), (xmax,0,0)], arrow_head=True,rgbcolor='black')
A=A+line3d([(0,ymin,0), (0,ymax,0)], arrow_head=True,rgbcolor='black')
A=A+line3d([(0,0,zmin), (0,0,zmax)], arrow_head=True,rgbcolor='black')
show(A)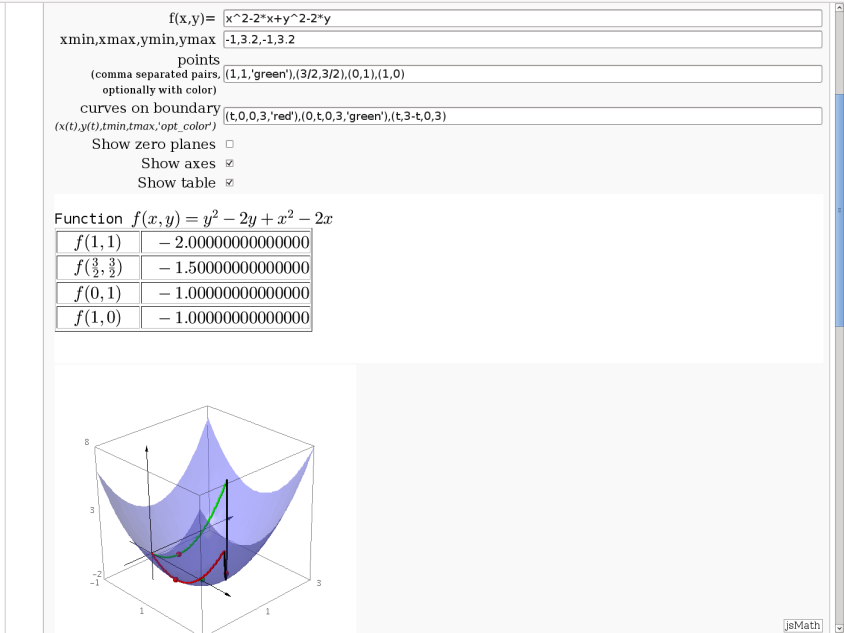
Approximating function in two variables by differential
by Robert Marik
x,y=var('x y')
html('<h2>Explaining approximation of a function in two \
variables by differential</h2>')
html('Points x0 and y0 are values where the exact value of the function \
is known. Deltax and Deltay are displacements of the new point. Exact value \
and approximation by differential at shifted point are compared.')
@interact
def _(func=input_box('sqrt(x^3+y^3)',label="f(x,y)=",type=str), x0=1, y0=2, \
deltax=slider(-1,1,0.01,0.2),\
deltay=slider(-1,1,0.01,-0.4), xmin=0, xmax=2, ymin=0, ymax=3):
f=sage_eval('lambda x,y: ' + func)
derx(x,y)=diff(f(x,y),x)
dery(x,y)=diff(f(x,y),y)
tangent(x,y)=f(x0,y0)+derx(x0,y0)*(x-x0)+dery(x0,y0)*(y-y0)
A=plot3d(f(x,y),(x,xmin,xmax),(y,ymin,ymax),opacity=0.5)
B=plot3d(tangent(x,y),(x,xmin,xmax),(y,ymin,ymax),color='red',opacity=0.5)
C=point3d((x0,y0,f(x0,y0)),rgbcolor='blue',size=9)
CC=point3d((x0+deltax,y0+deltay,f(x0+deltax,y0+deltay)),rgbcolor='blue',size=9)
D=point3d((x0+deltax,y0+deltay,tangent(x0+deltax,y0+deltay)),rgbcolor='red',size=9)
exact_value_ori=f(x0,y0).n(digits=10)
exact_value=f(x0+deltax,y0+deltay)
approx_value=tangent(x0+deltax,y0+deltay).n(digits=10)
abs_error=(abs(exact_value-approx_value))
html(r'Function $ f(x,y)=%s \approx %s $ '%(latex(f(x,y)),latex(tangent(x,y))))
html(r' $f %s = %s$'%(latex((x0,y0)),latex(exact_value_ori)))
html(r'Shifted point $%s$'%latex(((x0+deltax),(y0+deltay))))
html(r'Value of the function in shifted point is $%s$'%f(x0+deltax,y0+deltay))
html(r'Value on the tangent plane in shifted point is $%s$'%latex(approx_value))
html(r'Error is $%s$'%latex(abs_error))
show(A+B+C+CC+D)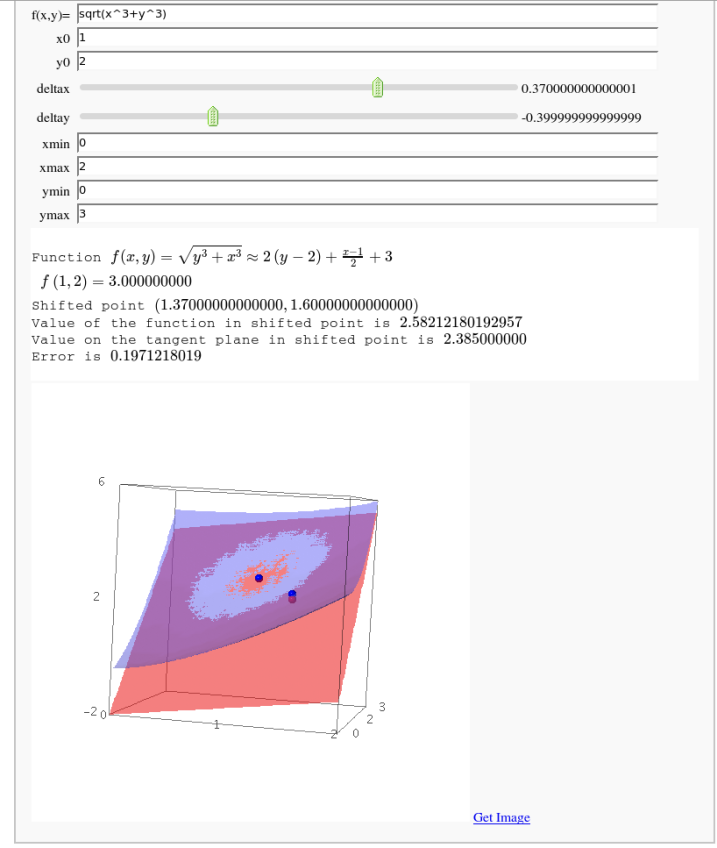
Taylor approximations in two variables
by John Palmieri
This displays the nth order Taylor approximation, for n from 1 to 10, of the function sin(x2 + y2) cos(y) exp(-(x2+y2)/2).
var('x y')
var('xx yy')
G = sin(xx^2 + yy^2) * cos(yy) * exp(-0.5*(xx^2+yy^2))
def F(x,y):
return G.subs(xx=x).subs(yy=y)
plotF = plot3d(F, (0.4, 2), (0.4, 2), adaptive=True, color='blue')
@interact
def _(x0=(0.5,1.5), y0=(0.5, 1.5),
order=(1..10)):
F0 = float(G.subs(xx=x0).subs(yy=y0))
P = (x0, y0, F0)
dot = point3d(P, size=15, color='red')
plot = dot + plotF
approx = F0
for n in range(1, order+1):
for i in range(n+1):
if i == 0:
deriv = G.diff(yy, n)
elif i == n:
deriv = G.diff(xx, n)
else:
deriv = G.diff(xx, i).diff(yy, n-i)
deriv = float(deriv.subs(xx=x0).subs(yy=y0))
coeff = binomial(n, i)/factorial(n)
approx += coeff * deriv * (x-x0)^i * (y-y0)^(n-i)
plot += plot3d(approx, (x, 0.4, 1.6),
(y, 0.4, 1.6), color='red', opacity=0.7)
html('$F(x,y) = e^{-(x^2+y^2)/2} \\cos(y) \\sin(x^2+y^2)$')
show(plot)