|
Size: 8456
Comment:
|
← Revision 15 as of 2019-04-06 06:18:49 ⇥
Size: 7597
Comment: py3 print
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| goto [:interact:interact main page] | goto [[interact|interact main page]] |
| Line 4: | Line 4: |
| [[TableOfContents]] | <<TableOfContents>> |
| Line 8: | Line 8: |
| {{{ | {{{#!sagecell |
| Line 18: | Line 18: |
| attachment:gfan_interact.png | {{attachment:gfan_interact.png}} |
| Line 20: | Line 20: |
| == 3D Groebner fan browser == | == 3D Groebner fan browser FIXME == |
| Line 22: | Line 22: |
| {{{ | {{{#!sagecell |
| Line 24: | Line 24: |
| """ A utility function that takes a 4d polytope, projects it to 3d, and returns a list of edges. INPUT: polyhedral_data -- an object with 4d vertex and adjacency information OUTPUT: """ |
|
| Line 46: | Line 37: |
| """ Returns solid 3d rendering of a 3d polytope. """ |
|
| Line 54: | Line 42: |
| """ For a Groebner fan of an ideal in a ring with four variables, this function intersects the fan with the standard simplex perpendicular to (1,1,1,1), creating a 3d polytope, which is then projected into 3 dimensions. The edges of this projected polytope are returned as lines. EXAMPLES: sage: R4.<w,x,y,z> = PolynomialRing(QQ,4) sage: gf = R4.ideal([w^2-x,x^2-y,y^2-z,z^2-x]).groebner_fan() sage: three_d = gf.render3d() """ |
|
| Line 73: | Line 49: |
| print x.ieqs() + [[1,1,0,0,0],[1,0,1,0,0],[1,0,0,1,0],[1,0,0,0,1]] print x.linearities() print "" |
print(x.ieqs() + [[1,1,0,0,0],[1,0,1,0,0],[1,0,0,1,0],[1,0,0,0,1]]) print(x.linearities()) print("") |
| Line 82: | Line 58: |
| degs = [[max([q.degree(avar) for q in b]) for avar in our_vars] for b in a_gf.reduced_groebner_bases()] maxdegs = [max([float(q[i]) for q in degs]) for i in range(len(our_vars))] |
degs = [[max(q.degree(avar) for q in b) for avar in our_vars] for b in a_gf.reduced_groebner_bases()] maxdegs = [max(float(q[i]) for q in degs) for i in range(len(our_vars))] |
| Line 85: | Line 61: |
| color_list = [tuple([c[i]/max(c) for i in range(3)]) for c in color_list] #print color_list |
color_list = [tuple(c[i]/max(c) for i in range(3)) for c in color_list] |
| Line 94: | Line 69: |
| #print cone_data | |
| Line 100: | Line 74: |
| if color_fan == True: #using fixed color scheme #print i, faces, color_list[i], cone_verts |
if color_fan == True: |
| Line 107: | Line 79: |
| print cone_data._rays | print(cone_data._rays) |
| Line 127: | Line 99: |
| print id_gens | print(id_gens) |
| Line 142: | Line 114: |
| attachment:gb3d.png | {{attachment:gb3d.png}} |
| Line 144: | Line 116: |
| == Numerical Solutions of Polynomial Systems with PHCpack == | == Numerical Solutions of Polynomial Systems with PHCpack FIXME == |
| Line 147: | Line 119: |
| {{{ | {{{#!sagecell from sage.interfaces.phc import phc |
| Line 189: | Line 162: |
| for i in len(pols): | for i in range(len(pols)): |
| Line 192: | Line 165: |
| attachment:pathtrack.png | {{attachment:pathtrack.png}} |
Sage Interactions - Algebra
goto interact main page
Contents
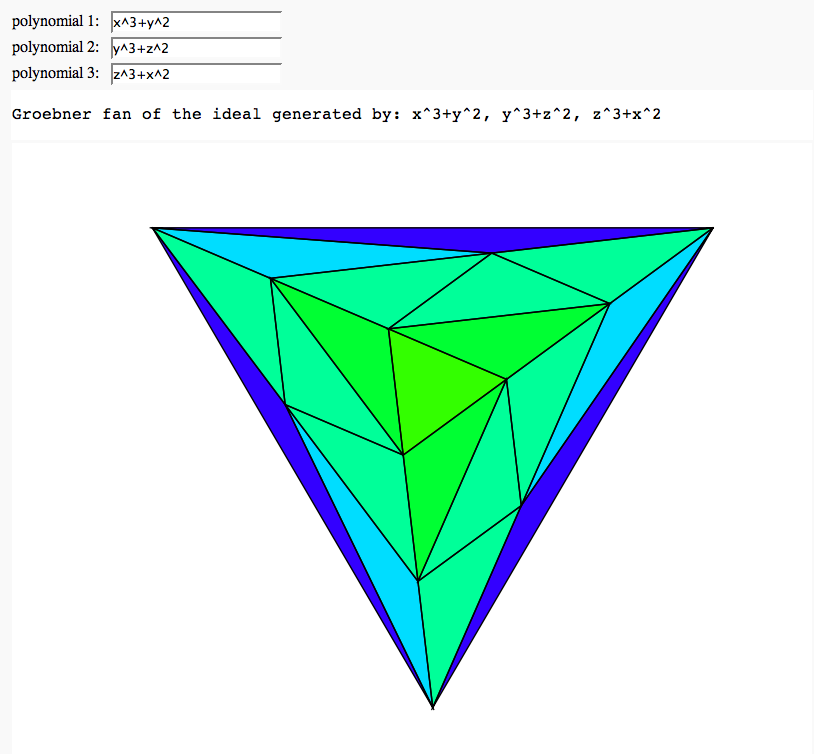
Groebner fan of an ideal
by Marshall Hampton; (needs sage-2.11 or higher, with gfan-0.3 interface)
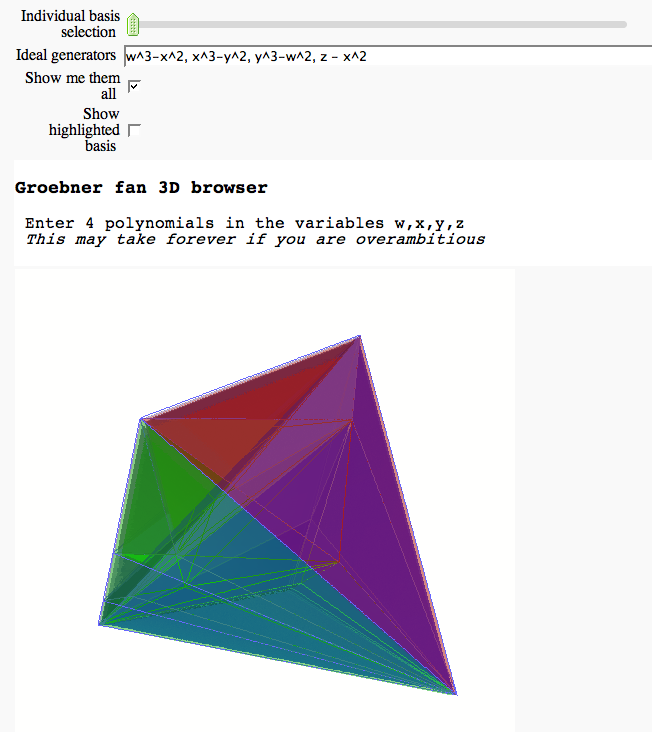
3D Groebner fan browser FIXME
by Marshall Hampton
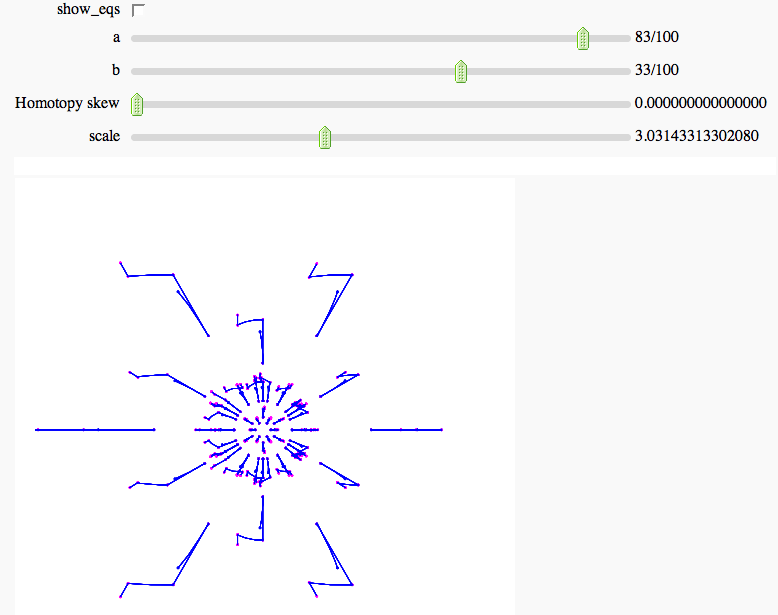
Numerical Solutions of Polynomial Systems with PHCpack FIXME
by Marshall Hampton; requires phcpack optional package (PHCpack written by Jan Verschelde). The example below is a two-parameter deformation of the cyclic-6 problem. Solution paths are tracked through the parameter homotopy.