|
Size: 3198
Comment:
|
← Revision 15 as of 2019-04-06 06:18:49 ⇥
Size: 7597
Comment: py3 print
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 2: | Line 2: |
| goto [:interact:interact main page] | goto [[interact|interact main page]] |
| Line 4: | Line 4: |
| [[TableOfContents]] | <<TableOfContents>> |
| Line 8: | Line 8: |
| {{{ | {{{#!sagecell |
| Line 18: | Line 18: |
| attachment:gfan_interact.png | {{attachment:gfan_interact.png}} |
| Line 20: | Line 20: |
| == Numerical Solutions of Polynomial Systems with PHCpack == | == 3D Groebner fan browser FIXME == by Marshall Hampton {{{#!sagecell def proj4_to_3(gfanobj, poly4): fpoints = poly4.vertices() tpoints = [gfanobj._embed_tetra(q) for q in fpoints] adj_data = poly4.vertex_adjacencies() edges = [] for adj in adj_data: for vert in adj[1]: if vert > adj[0]: edges.append([tpoints[adj[0]],tpoints[vert]]) return edges, tpoints from sage.plot.plot3d.index_face_set import IndexFaceSet def render_solid(poly, color = 'blue', opacity = .5): tri_faces = poly.triangulated_facial_incidences() from sage.plot.plot3d.index_face_set import IndexFaceSet return IndexFaceSet([q[1] for q in tri_faces], poly.vertices(), enclosed = True, color = color, opacity = opacity) def render3d(a_gf, color_fan = True, verbose = False, highlights = 'all'): g_cones = [q.groebner_cone() for q in a_gf.reduced_groebner_bases()] g_cones_facets = [q.facets() for q in g_cones] g_cones_ieqs = [a_gf._cone_to_ieq(q) for q in g_cones_facets] # Now the cones are intersected with a plane: cone_info = [ieq_to_vert(q,linearities=[[1,-1,-1,-1,-1]]) for q in g_cones_ieqs] if verbose: for x in cone_info: print(x.ieqs() + [[1,1,0,0,0],[1,0,1,0,0],[1,0,0,1,0],[1,0,0,0,1]]) print(x.linearities()) print("") cone_info = [Polyhedron(ieqs = x.ieqs() + [[1,1,0,0,0],[1,0,1,0,0],[1,0,0,1,0],[1,0,0,0,1]], linearities = x.linearities()) for x in cone_info] if color_fan == True: #using fixed color scheme color_list = [] our_vars = list(a_gf.ring().gens()) degs = [[max(q.degree(avar) for q in b) for avar in our_vars] for b in a_gf.reduced_groebner_bases()] maxdegs = [max(float(q[i]) for q in degs) for i in range(len(our_vars))] color_list = [[b[0]/maxdegs[0],b[1]/maxdegs[1],(b[2]+b[3])/(maxdegs[2]+maxdegs[3])] for b in degs] color_list = [tuple(c[i]/max(c) for i in range(3)) for c in color_list] faces = [] if highlights == 'all': highlights = range(len(cone_info)) all_lines = [] i = 0 for cone_data in cone_info: # cone_data is a Polyhedron. try: pdata = proj4_to_3(a_gf,cone_data) cone_lines = pdata[0] cone_verts = pdata[1] if color_fan == True: if i in highlights: faces.append(render_solid(Polyhedron(vertices = cone_verts), color = color_list[i])) i = i + 1 except: print(cone_data._rays) raise RuntimeError for a_line in cone_lines: all_lines.append(a_line) if faces == []: faceadds = Graphics() else: faceadds = sum(faces) return sum([line3d(a_line) for a_line in all_lines]) + faceadds R4.<w,x,y,z> = PolynomialRing(QQ,4) temp_id = R4.ideal([w^3-x^2, x^3-y^21, y^3-w^2, z - x^2]) temp_gf4 = temp_id.groebner_fan() temp_gf4_rbs = temp_gf4.reduced_groebner_bases() gbdict = dict([['w^3-x^2, x^3-y^2, y^3-w^2, z - x^2',(temp_gf4,temp_gf4_rbs)]]) @interact def Groebner_fan_browser(bsel = slider(0,100,.1,0,label='Individual basis selection', display_value = False), ideal_gens = input_box(default = 'w^3-x^2, x^3-y^2, y^3-w^2, z - x^2', type = str, label = "Ideal generators"), showall = checkbox(True, "Show me them all"), showbases = checkbox(False, "Show highlighted basis")): html('<h3>Groebner fan 3D browser</h3> Enter 4 polynomials in the variables w,x,y,z<BR> <em>This may take forever if you are overambitious</em>') R4.<w,x,y,z> = PolynomialRing(QQ,4) if ideal_gens not in gbdict: id_gens = R4.ideal(list(ideal_gens.split(','))) print(id_gens) gf4 = id_gens.groebner_fan() gf4rbs = gf4.reduced_groebner_bases() gbdict[ideal_gens] = (gf4,gf4rbs) else: gf4 = gbdict[ideal_gens][0] gf4rbs = gbdict[ideal_gens][1] bnumbers = len(gf4rbs) b_select = [int(bsel*bnumbers/100.0)] if showall: b_select = range(bnumbers) if showbases: for b in b_select: show(gf4rbs[b]) show(render3d(gf4, highlights = b_select), frame = False) }}} {{attachment:gb3d.png}} == Numerical Solutions of Polynomial Systems with PHCpack FIXME == |
| Line 23: | Line 119: |
| {{{ | {{{#!sagecell from sage.interfaces.phc import phc |
| Line 65: | Line 162: |
| for i in len(pols): | for i in range(len(pols)): |
| Line 68: | Line 165: |
| attachment:pathtrack.png | {{attachment:pathtrack.png}} |
Sage Interactions - Algebra
goto interact main page
Contents
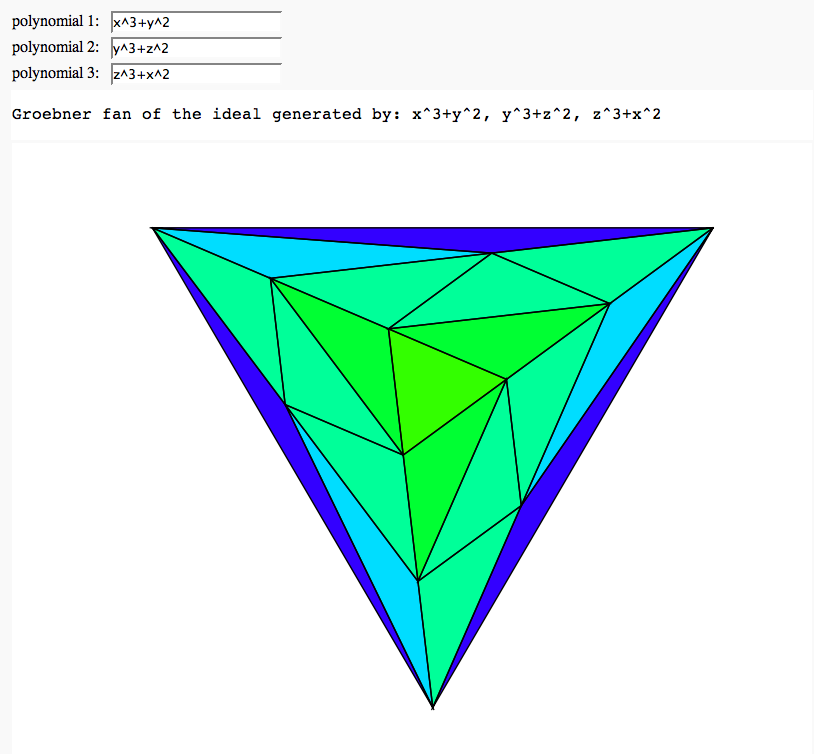
Groebner fan of an ideal
by Marshall Hampton; (needs sage-2.11 or higher, with gfan-0.3 interface)
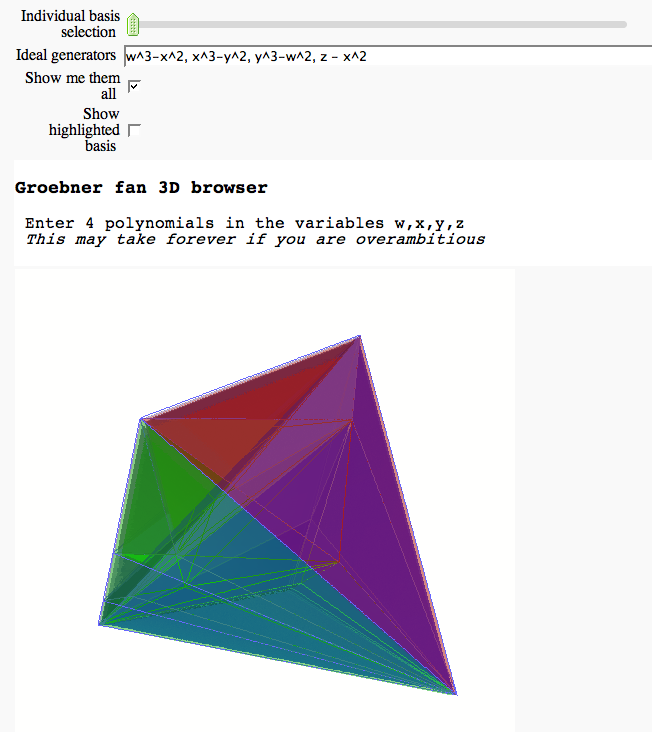
3D Groebner fan browser FIXME
by Marshall Hampton
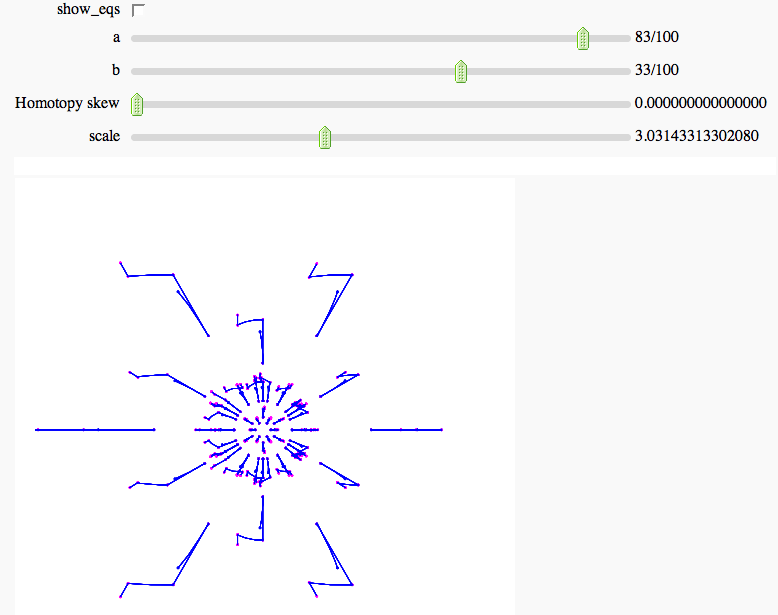
Numerical Solutions of Polynomial Systems with PHCpack FIXME
by Marshall Hampton; requires phcpack optional package (PHCpack written by Jan Verschelde). The example below is a two-parameter deformation of the cyclic-6 problem. Solution paths are tracked through the parameter homotopy.