Differences between revisions 19 and 28 (spanning 9 versions)
⇤ ← Revision 19 as of 2007-06-12 21:12:12 →
Size: 9244
Editor: anonymous
Comment:
← Revision 28 as of 2008-11-14 13:41:50 → ⇥
Size: 12645
Editor: anonymous
Comment: converted to 1.6 markup
Deletions are marked like this. Additions are marked like this.
Line 1: Line 1:
Emily Kirkman is working on this project. [http://sage.math.washington.edu:9001/graph Back to main wiki.] The Cayley graph for $A_5$:

{{{
sage: G = sage.groups.perm_gps.permgroup.AlternatingGroup(5)
sage: C = G.cayley_graph()
sage: C.show3d(bgcolor=(0,0,0), arc_color=(1,1,1), vertex_size=0.02, arc_size=0.007, arc_size2=0.01, xres=1000, yres=800, iterations=200)
}}}

{{attachment:A5.jpg}}

Emily Kirkman and Robert Miller are working on this project. [[http://wiki.sagemath.org/graph|Back to main wiki.]]
Line 5: Line 15:
We currently have 30 constructors of named graphs and basic structures. Most of these graphs are constructed with a preset dictionary of x-y coordinates of each node. This is advantageous for both style and time. (The default graph plotting in SAGE uses the spring-layout algorithm). SAGE graphs all have an associated graphics object, and examples of plotting options are shown on the graphs below. We currently have 54 constructors of named graphs and basic structures. Most of these graphs are constructed with a preset dictionary of x-y coordinates of each node. This is advantageous for both style and time. (The default graph plotting in SAGE uses the spring-layout algorithm). SAGE graphs all have an associated graphics object, and examples of plotting options are shown on the graphs below.
Line 9: Line 19:
Due to the volume of graphs now in the generators class, this wiki page is now intended to give status updates and serve as a gallery of graphs currently implemented. To see information on a specific graph, run SAGE or the SAGE [http://sage.math.washington.edu:8100 notebook]. For a list of graph constructors, type "graphs." and hit tab. For docstrings, type the graph name and one question mark (i.e.: "graphs.!CubeGraph?") then shift + enter. For source code, do likewise with two question marks.

[[TableOfContents]]		 Due to the volume of graphs now in the generators class, this wiki page is now intended to give status updates and serve as a gallery of graphs currently implemented. To see information on a specific graph, run SAGE or the SAGE [[http://sage.math.washington.edu:8100|notebook]]. For a list of graph constructors, type "graphs." and hit tab. For docstrings, type the graph name and one question mark (i.e.: "graphs.!CubeGraph?") then shift + enter. For source code, do likewise with two question marks.

<<TableOfContents>>
Line 20: Line 30:
 * Balanced tree
 * Dorogovstev golstev mendes graph
Line 23: Line 31:
 * Chvatal
 * Desargues
 * Pappus
Line 30: Line 35:
 * Also many more random generators and gens from degree sequence to sort through
Line 42: Line 46:
 * Icosahedron
Line 55: Line 58:
{{{
sage: (graphs.ChvatalGraph()).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:chvatal.png}}
Line 57: Line 64:
{{{
sage: (graphs.DesarguesGraph()).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:desargues.png}}
Line 64: Line 75:
attachment:flower.png {{attachment:flower.png}}
Line 71: Line 82:
attachment:frucht.png {{attachment:frucht.png}}
Line 78: Line 89:
attachment:heawood.png
 {{attachment:heawood.png}}
Line 86: Line 96:
attachment:moebiuskantor.png {{attachment:moebiuskantor.png}}
Line 89: Line 99:
{{{
sage: (graphs.PappusGraph()).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:pappus.png}}
Line 95: Line 109:
attachment:petersen.png {{attachment:petersen.png}}
Line 102: Line 116:
attachment:thomsen.png {{attachment:thomsen.png}}
Line 115: Line 129:
attachment:compbip.png {{attachment:compbip.png}}
Line 125: Line 139:
attachment:complete.png {{attachment:complete.png}}
Line 135: Line 149:
attachment:cube.png {{attachment:cube.png}}
Line 141: Line 155:
attachment:biggercube.png {{attachment:biggercube.png}}
Line 144: Line 158:
{{{
sage: (graphs.BalancedTree(3,5)).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)
}}}
{{attachment:baltree.png}}
Line 146: Line 164:
{{{
sage: (graphs.LCFGraph(20, [-10,-7,-5,4,7,-10,-7,-4,5,7,-10,-7,6,-5,7,-10,-7,5,-6,7], 1)).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:lcf.png}}
Line 154: Line 176:
attachment:tetrahedral.png {{attachment:tetrahedral.png}}
Line 157: Line 179:
{{{
sage: (graphs.HexahedralGraph()).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:hexahedral.png}}
Line 163: Line 189:
attachment:octahedral.png {{attachment:octahedral.png}}
Line 166: Line 192:
{{{
sage: (graphs.IcosahedralGraph()).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:icosahedral.png}}
Line 172: Line 202:
attachment:dodecahedral.png {{attachment:dodecahedral.png}}
Line 177: Line 207:
{{{
sage: (graphs.DorogovtsevGoltsevMendesGraph(5)).show(figsize=[4,4], graph_border=True, vertex_size=10, vertex_labels=False)
}}}
{{attachment:tmp_6.png}}
Line 189: Line 223:
attachment:barbell.png {{attachment:barbell.png}}
Line 196: Line 230:
attachment:bull.png {{attachment:bull.png}}
Line 203: Line 237:
attachment:circladder.png {{attachment:circladder.png}}
Line 210: Line 244:
attachment:claw.png {{attachment:claw.png}}
Line 217: Line 251:
attachment:cycle.png {{attachment:cycle.png}}
Line 224: Line 258:
attachment:diamond.png {{attachment:diamond.png}}
Line 231: Line 265:
attachment:empty.png {{attachment:empty.png}}
Line 238: Line 272:
attachment:grid.png {{attachment:grid.png}}
Line 245: Line 279:
attachment:house.png {{attachment:house.png}}
Line 252: Line 286:
attachment:housex.png {{attachment:housex.png}}
Line 259: Line 293:
attachment:krack.png {{attachment:krack.png}}
Line 266: Line 300:
attachment:ladder.png {{attachment:ladder.png}}
Line 277: Line 311:
attachment:lollipop.png {{attachment:lollipop.png}}
Line 287: Line 321:
attachment:path.png {{attachment:path.png}}
Line 297: Line 331:
attachment:star.png {{attachment:star.png}}
Line 307: Line 341:
attachment:wheel.png {{attachment:wheel.png}}
Line 319: Line 353:
attachment:random.png {{attachment:random.png}}
Line 329: Line 363:
attachment:randomfast.png {{attachment:randomfast.png}}
Line 332: Line 366:
{{{
sage: (graphs.RandomBarabasiAlbert(7,3)).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:barabasi.png}}
Line 334: Line 372:

=== Random Neewman Watts Strogatz ===		 {{{
sage: (graphs.RandomGNM(7,16)).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:gnm.png}}

=== Random Newman Watts Strogatz ===
{{{
sage: (graphs.RandomNewmanWattsStrogatz(7,3,.5)).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:newman.png}}
Line 338: Line 384:
{{{
sage: (graphs.RandomHolmeKim(12,3,.4)).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:holme.png}}
Line 340: Line 390:
{{{
sage: (graphs.RandomHolmeKim(12,3,.4)).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:lobster.png}}
Line 342: Line 396:
{{{
sage: (graphs.RandomTreePowerlaw(15)).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:powerlaw.png}}
Line 344: Line 402:
{{{
sage: (graphs.RandomRegular(3,20)).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)
}}}
{{attachment:randreg.png}}
Line 346: Line 408:
{{{
sage: (graphs.RandomShell([(10,20,0.8),(20,40,0.8)])).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)
}}}
{{attachment:shell.png}}
Line 350: Line 416:
{{{
sage: (graphs.RandomDirectedGN(12)).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)
}}}
{{attachment:randdirgn.png}}
Line 352: Line 422:
{{{
sage: (graphs.RandomDirectedGNC(12)).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)
}}}
{{attachment:randdirgnc.png}}
Line 354: Line 428:
{{{
sage: (graphs.RandomDirectedGNR(12,.15)).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)
}}}
{{attachment:randdirgnr.png}}
Line 358: Line 436:
{{{
sage: (graphs.DegreeSequence([3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3])).show(vertex_labels=False, node_size=30, figsize=[4,4], graph_border=True)
}}}
{{attachment:degseq.png}}
Line 360: Line 442:
{{{
sage: (graphs.DegreeSequenceConfigurationModel([3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3])).show(vertex_labels=False, node_size=30, figsize=[4,4], graph_border=True)
}}}
{{attachment:degseqconf.png}}
Line 362: Line 448:
{{{
sage: (graphs.DegreeSequenceTree([3,1,3,3,1,1,1,2,1])).show(figsize=[4,4], graph_border=True)
}}}
{{attachment:degseqtree.png}}
Line 364: Line 454:
{{{
sage: (graphs.DegreeSequenceExpected([1,2,3,2,3])).show(figsize=[4,4],graph_border=True)
}}}
{{attachment:degseqexp.png}}

The Cayley graph for A_5: 

sage: G = sage.groups.perm_gps.permgroup.AlternatingGroup(5)
sage: C = G.cayley_graph()
sage: C.show3d(bgcolor=(0,0,0), arc_color=(1,1,1), vertex_size=0.02, arc_size=0.007, arc_size2=0.01, xres=1000, yres=800, iterations=200)

A5.jpg

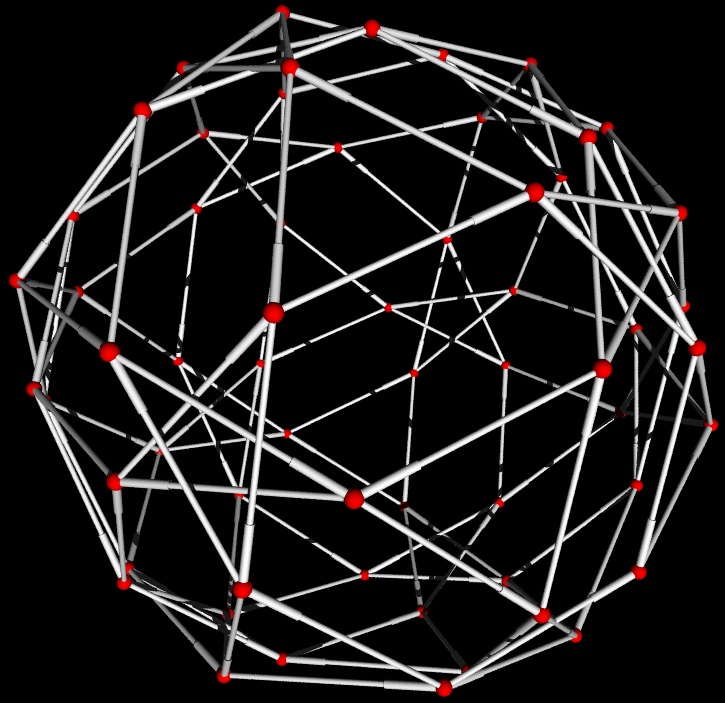
Emily Kirkman and Robert Miller are working on this project. Back to main wiki.

The goal of the Graph Generators Class is to implement constructors for many common graphs, as well as thorough docstrings that can be used for reference. The graph generators will grow as the Graph Theory Project does. So please check back for additions and feel free to leave requests in the suggestions section.

We currently have 54 constructors of named graphs and basic structures. Most of these graphs are constructed with a preset dictionary of x-y coordinates of each node. This is advantageous for both style and time. (The default graph plotting in SAGE uses the spring-layout algorithm). SAGE graphs all have an associated graphics object, and examples of plotting options are shown on the graphs below.

As we implement algorithms into the Graph Theory Package, the constructors of known graphs would set their properties upon instantiation as well. For example, if someone created a very large complete bipartite graph and then asked if it is a bipartite graph (not currently implemented), then instead of running through an algorithm to check it, we could return a value set at instantiation. Further, this will improve the reference use of the docstrings as we would list the properties of each named graph.

Due to the volume of graphs now in the generators class, this wiki page is now intended to give status updates and serve as a gallery of graphs currently implemented. To see information on a specific graph, run SAGE or the SAGE notebook. For a list of graph constructors, type "graphs." and hit tab. For docstrings, type the graph name and one question mark (i.e.: "graphs.CubeGraph?") then shift + enter. For source code, do likewise with two question marks.

Contents

  1. Suggestions
  2. Graphs I Plan to Add
    1. Inherited from NetworkX
    2. Families of Graphs
    3. Named Graphs
  3. Gallery of Graph Generators in SAGE
    1. Named Graphs
      1. Chvatal Graph
      2. Desargues Graph
      3. Flower Snark
      4. Frucht
      5. Heawood
      6. Möbius Kantor
      7. Pappus Graph
      8. Petersen
      9. Thomsen
    2. Graph Families
      1. Complete Bipartite Graphs
      2. Complete Graphs
      3. Cube Graphs
      4. Balanced Tree
      5. LCF Graph
    3. Platonic Solids
      1. Tetrahedral Graph
      2. Hexahedral Graph
      3. Octahedral Graph
      4. Icosahedral Graph
      5. Dodecahedral Graph
    4. Pseudofractal Graphs
      1. Dorogovtsev Goltsev Mendes Graph
    5. Basic Structures
      1. Barbell Graph
      2. Bull Graph
      3. Circular Ladder Graph
      4. Claw Graph
      5. Cycle Graphs
      6. Diamond Graph
      7. Empty Graph
      8. Grid 2d Graph
      9. House Graph
      10. House X Graph
      11. Krackhardt Kite Graph
      12. Ladder Graph
      13. Lollipop Graph
      14. Path Graph
      15. Star Graph
      16. Wheel Graph
    6. Random Generators
      1. Random GNP
      2. Random GNP Fast
      3. Random Barabasi Albert
      4. Random GNM
      5. Random Newman Watts Strogatz
      6. Random Holme Kim
      7. Random Lobster
      8. Random Tree Powerlaw
      9. Random Regular
      10. Random Shell
    7. Random Directed Graphs
      1. Random Directed GN
      2. Random Directed GNC
      3. Random Directed GNR
    8. Graphs With a Given Degree Sequence
      1. Degree Sequence
      2. Degree Sequence Configuration Model
      3. Degree Sequence Tree
      4. Degree Sequence Expected

Suggestions

  • ???

Graphs I Plan to Add

Inherited from NetworkX

  • Bipartite Generators
  • Grid (n-dim)
  • Sedgewick
  • Truncated cube
  • Truncated tetrahedron
  • Tutte

Families of Graphs

  • Generalized Petersen graphs
  • Petersen Graph family
  • Trees (Directed – not simple. Maybe Balanced tree constructor and query isTree)
  • Cayley (Requires Edge Coloring)
  • Paley

Named Graphs

  • Brinkman
  • Clebsch
  • Grötzsch graph
  • Tutte eight-cage
  • Szekeres snark
  • Thomassen graph
  • Johnson (maybe own class)
  • Turan

Gallery of Graph Generators in SAGE

Named Graphs

Chvatal Graph

sage: (graphs.ChvatalGraph()).show(figsize=[4,4], graph_border=True)

chvatal.png

Desargues Graph

sage: (graphs.DesarguesGraph()).show(figsize=[4,4], graph_border=True)

desargues.png

Flower Snark

sage: flower_snark = graphs.FlowerSnark()
sage: flower_snark.set_boundary([15,16,17,18,19])
sage: flower_snark.show(figsize=[4,4], graph_border=True)

flower.png

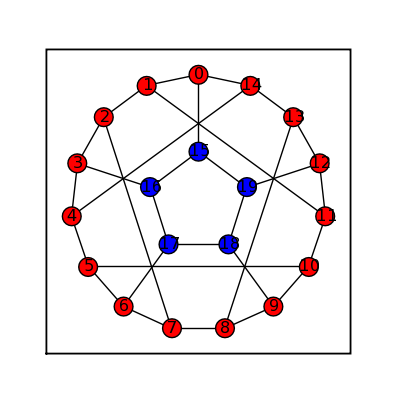
Frucht

sage: frucht = graphs.FruchtGraph()
sage: frucht.show(figsize=[4,4], graph_border=True)

frucht.png

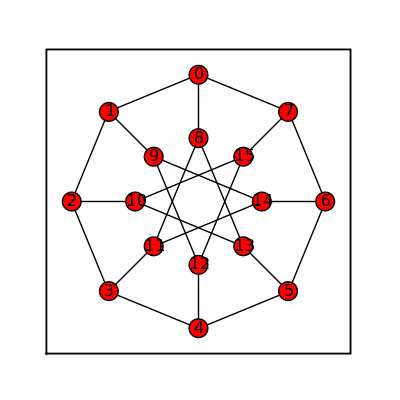
Heawood

sage: heawood = graphs.HeawoodGraph()
sage: heawood.show(figsize=[4,4], graph_border=True)

heawood.png

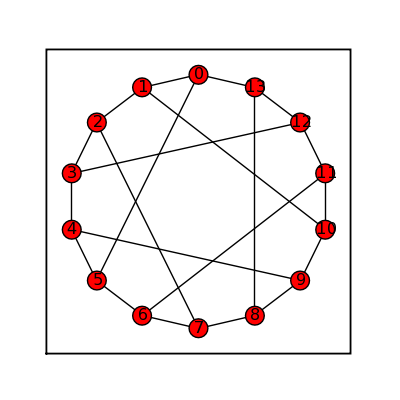
Möbius Kantor

sage: moebius_kantor = graphs.MoebiusKantorGraph()
sage: moebius_kantor.show(figsize=[4,4], graph_border=True)

moebiuskantor.png

Pappus Graph

sage: (graphs.PappusGraph()).show(figsize=[4,4], graph_border=True)

pappus.png

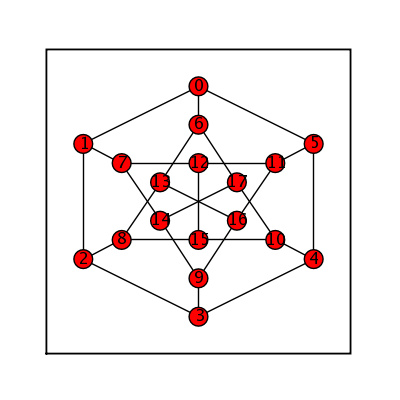
Petersen

sage: petersen = graphs.PetersenGraph()
sage: petersen.show(figsize=[4,4], graph_border=True)

petersen.png

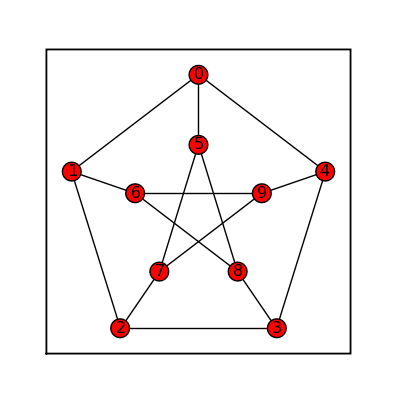
Thomsen

sage: thomsen = graphs.ThomsenGraph()
sage: thomsen.show(figsize=[4,4], graph_border=True)

thomsen.png

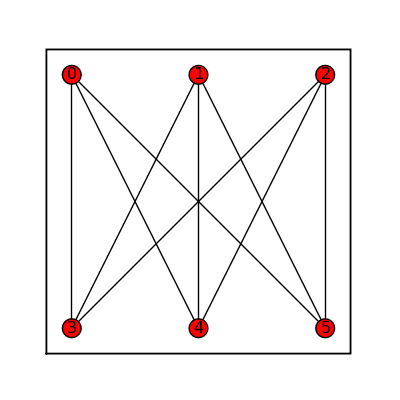
Graph Families

Complete Bipartite Graphs

sage: comp_bip_list = []
sage: for i in range (2):
... for j in range (4):
...  comp_bip_list.append(graphs.CompleteBipartiteGraph(i+3,j+1))
...
sage: graphs_list.show_graphs(comp_bip_list)

compbip.png

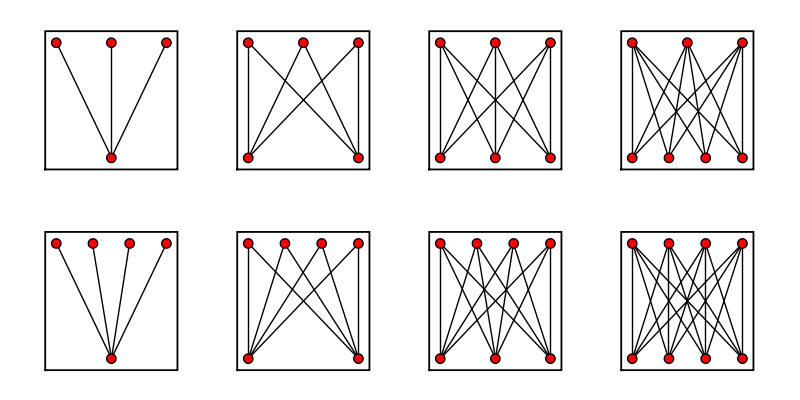
Complete Graphs

sage: comp_list = []
sage: for i in range(13)[1:]:
... comp_list.append(graphs.CompleteGraph(i))
...
sage: graphs_list.show_graphs(comp_list)

complete.png

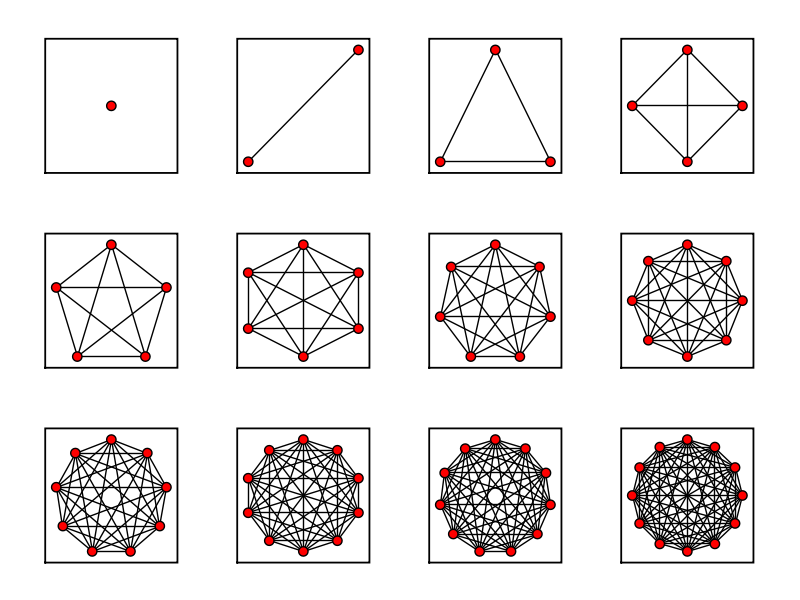
Cube Graphs

sage: cube_list = []
sage: for i in range(6)[2:]:
... cube_list.append(graphs.CubeGraph(i))
...
sage: graphs_list.show_graphs(cube_list)

cube.png 

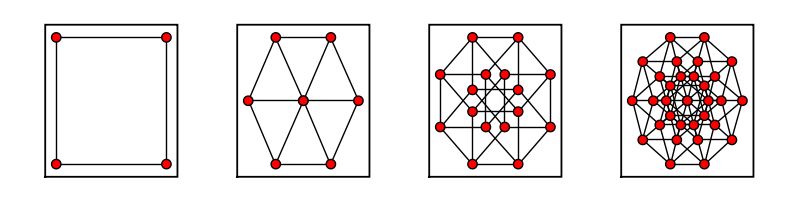
sage: bigger_cube = graphs.CubeGraph(8)
sage: bigger_cube.show(figsize=[8,8], node_size=20, vertex_labels=False, graph_border=True)

biggercube.png

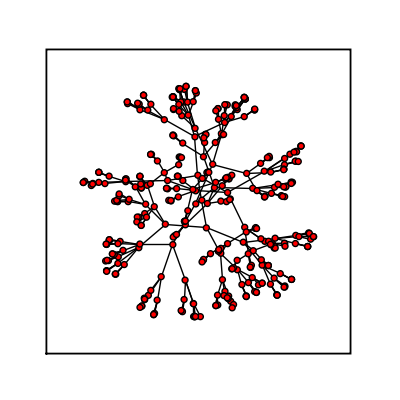
Balanced Tree

sage: (graphs.BalancedTree(3,5)).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)

baltree.png

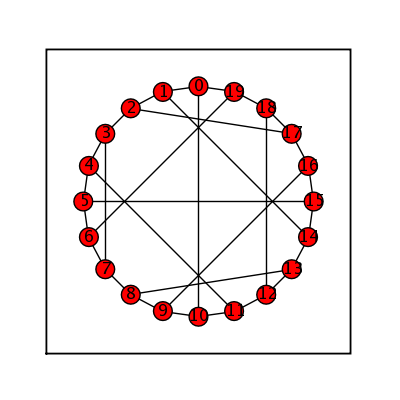
LCF Graph

sage: (graphs.LCFGraph(20, [-10,-7,-5,4,7,-10,-7,-4,5,7,-10,-7,6,-5,7,-10,-7,5,-6,7], 1)).show(figsize=[4,4], graph_border=True)

lcf.png

Platonic Solids

Tetrahedral Graph

sage: tetrahedral = graphs.TetrahedralGraph()
sage: tetrahedral.show(figsize=[4,4], graph_border=True)

tetrahedral.png

Hexahedral Graph

sage: (graphs.HexahedralGraph()).show(figsize=[4,4], graph_border=True)

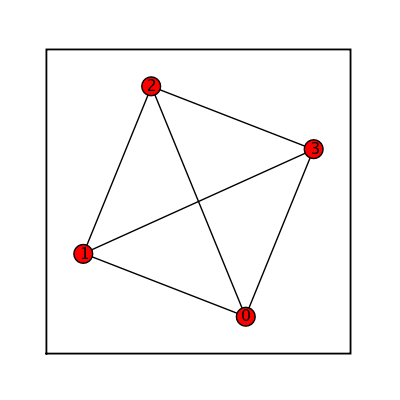
hexahedral.png

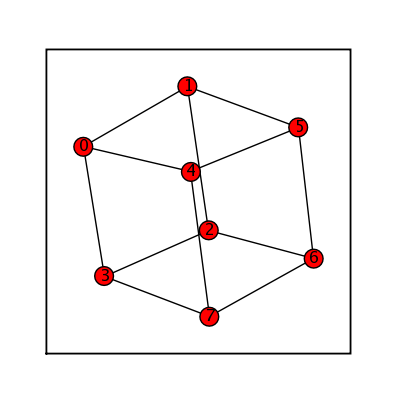
Octahedral Graph

sage: octahedral = graphs.OctahedralGraph()
sage: octahedral.show(figsize=[4,4], vertex_labels=False, node_size=50, graph_border=True)

octahedral.png

Icosahedral Graph

sage: (graphs.IcosahedralGraph()).show(figsize=[4,4], graph_border=True)

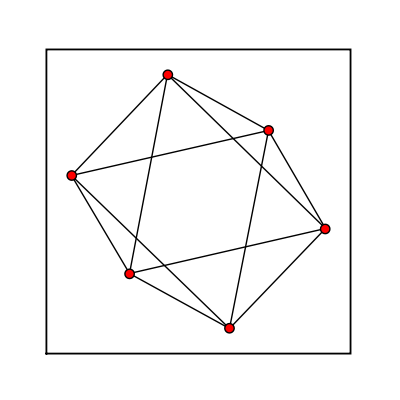
icosahedral.png

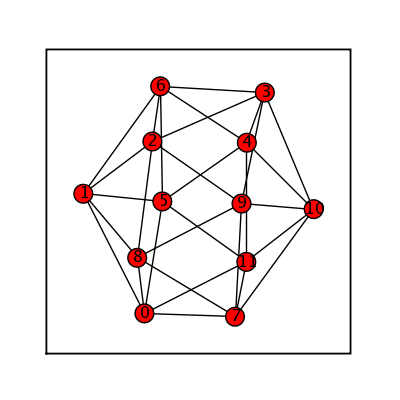
Dodecahedral Graph

sage: dodecahedral = graphs.DodecahedralGraph()
sage: dodecahedral.show(figsize=[4,4], vertex_labels=False, node_size=50, graph_border=True)

dodecahedral.png

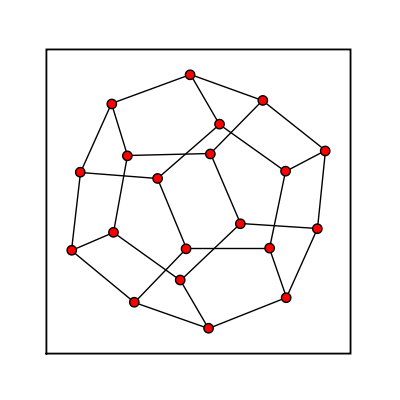
Pseudofractal Graphs

Dorogovtsev Goltsev Mendes Graph

sage: (graphs.DorogovtsevGoltsevMendesGraph(5)).show(figsize=[4,4], graph_border=True, vertex_size=10, vertex_labels=False)

tmp_6.png

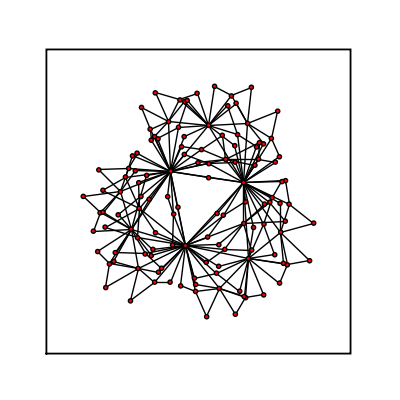
Basic Structures

Barbell Graph

sage: barbell_list = []
sage: for i in range (4):
... for j in range (2):
...  barbell_list.append(graphs.BarbellGraph(i+3, j+2))
...
sage: graphs_list.show_graphs(barbell_list)

barbell.png

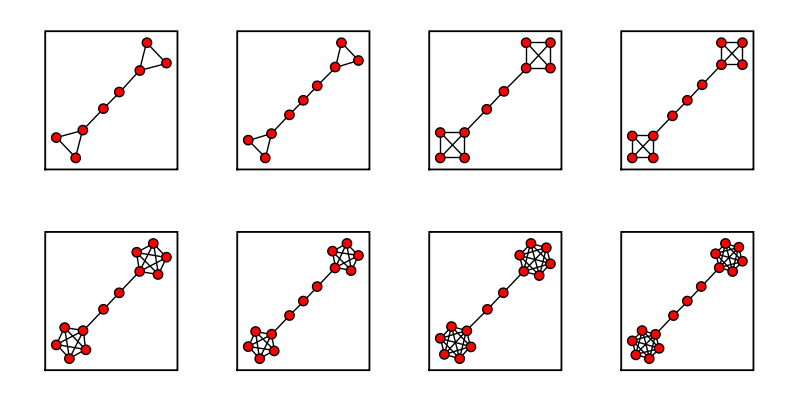
Bull Graph

sage: bull = graphs.BullGraph()
sage: bull.show(figsize=[4,4], graph_border=True)

bull.png

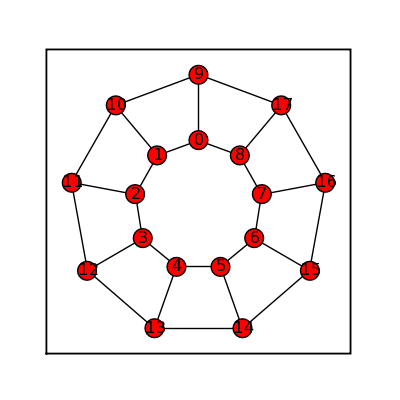
Circular Ladder Graph

sage: circ_ladder = graphs.CircularLadderGraph(9)
sage: circ_ladder.show(figsize=[4,4], graph_border=True)

circladder.png

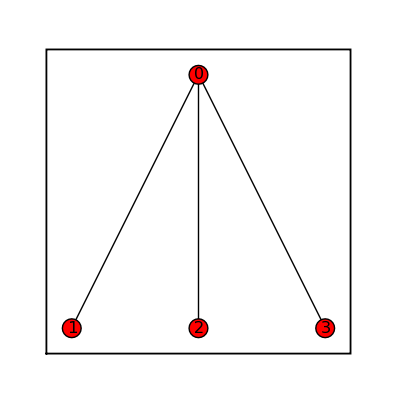
Claw Graph

sage: claw = graphs.ClawGraph()
sage: claw.show(figsize=[4,4], graph_border=True)

claw.png

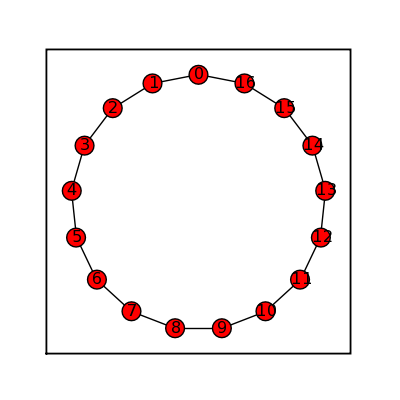
Cycle Graphs

sage: cycle = graphs.CycleGraph(17)
sage: cycle.show(figsize=[4,4], graph_border=True)

cycle.png

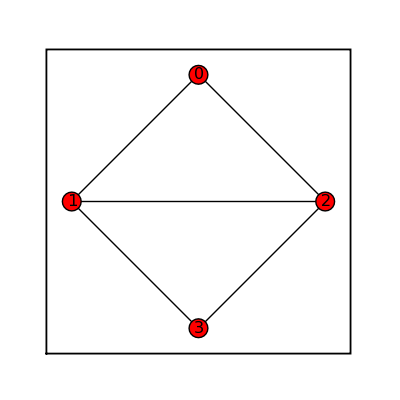
Diamond Graph

sage: diamond = graphs.DiamondGraph()
sage: diamond.show(figsize=[4,4], graph_border=True)

diamond.png

Empty Graph

sage: empty = graphs.EmptyGraph()
sage: empty.show(figsize=[1,1], graph_border=True)

empty.png

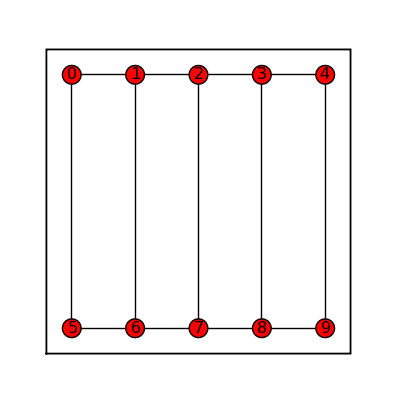
Grid 2d Graph

sage: grid = graphs.Grid2dGraph(3,5)
sage: grid.show(figsize=[5,3])

grid.png

House Graph

sage: house = graphs.HouseGraph()
sage: house.show(figsize=[4,4], graph_border=True)

house.png

House X Graph

sage: houseX = graphs.HouseXGraph()
sage: houseX.show(figsize=[4,4], graph_border=True)

housex.png

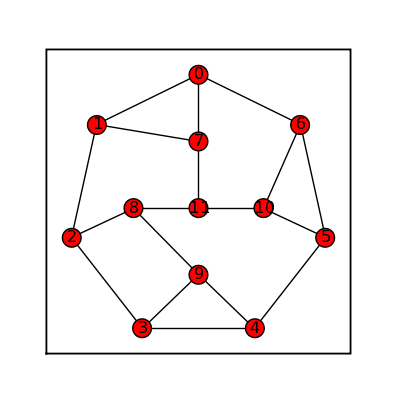
Krackhardt Kite Graph

sage: krackhardt = graphs.KrackhardtKiteGraph()
sage: krackhardt.show(figsize=[4,4], graph_border=True)

krack.png

Ladder Graph

sage: ladder = graphs.LadderGraph(5)
sage: ladder.show(figsize=[4,4], graph_border=True)

ladder.png

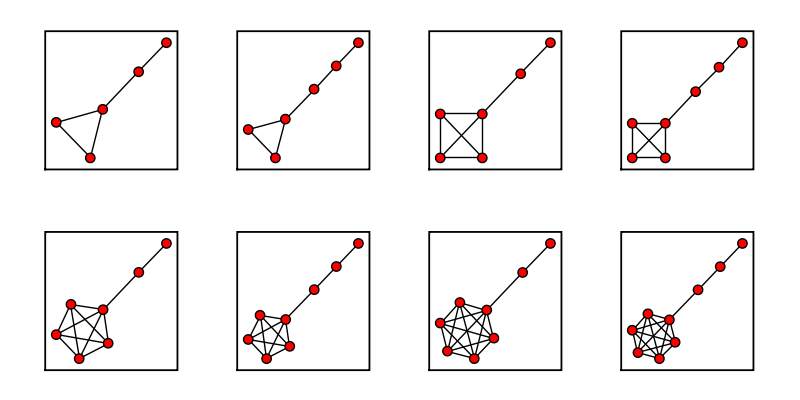
Lollipop Graph

sage: lollipop_list = []
sage: for i in range (4):
... for j in range (2):
...  lollipop_list.append(graphs.LollipopGraph(i+3, j+2))
...
sage: graphs_list.show_graphs(lollipop_list)

lollipop.png

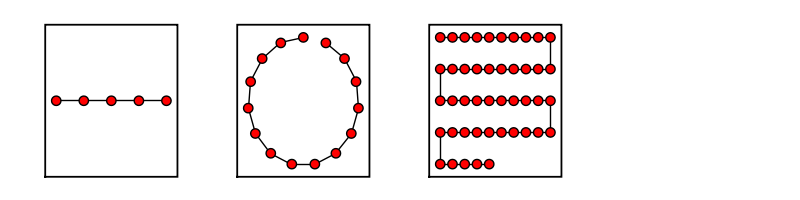
Path Graph

sage: path_line = graphs.PathGraph(5)
sage: path_circle = graphs.PathGraph(15)
sage: path_maze = graphs.PathGraph(45)
sage: path_list = [path_line, path_circle, path_maze]
sage: graphs_list.show_graphs(path_list)

path.png

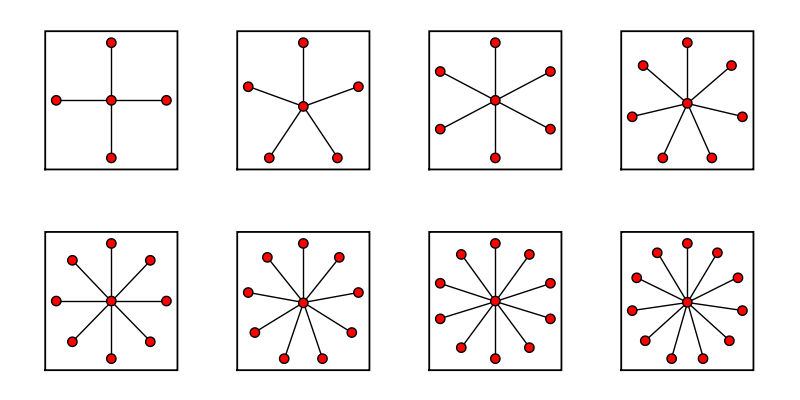
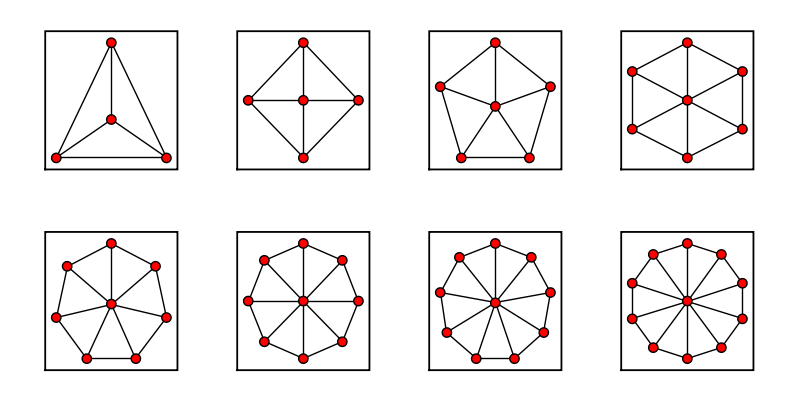
Star Graph

sage: star_list = []
sage: for i in range (12)[4:]:
... star_list.append(graphs.StarGraph(i))
...
sage: graphs_list.show_graphs(star_list)

star.png

Wheel Graph

sage: wheel_list = []
sage: for i in range (12)[4:]:
... wheel_list.append(graphs.WheelGraph(i))
...
sage: graphs_list.show_graphs(wheel_list)

wheel.png

Random Generators

Random GNP

Use for dense graphs: 

time
sage: (graphs.RandomGNP(16,.77)).show(figsize=[4,4], graph_border=True)

My results: CPU time: 0.74 s, Wall time: 0.73 s 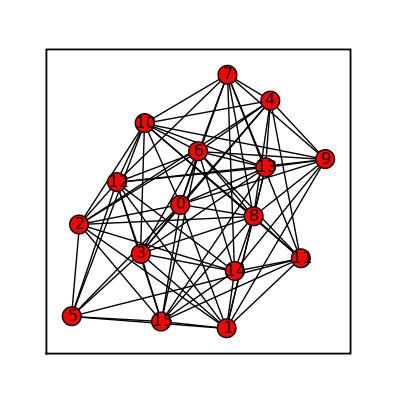random.png

Random GNP Fast

Use for sparse graphs: 

time
sage: (graphs.RandomGNPFast(16,.19)).show(figsize=[4,4], graph_border=True)

My results: CPU time: 0.63 s, Wall time: 0.62 s 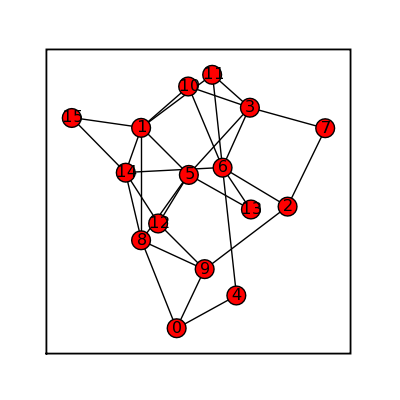randomfast.png

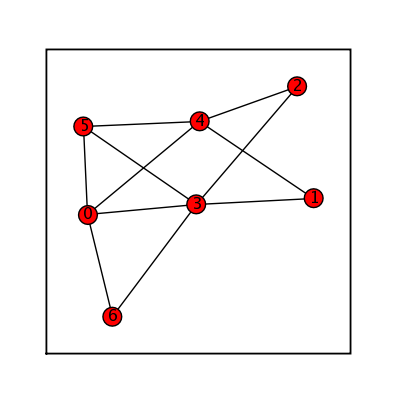
Random Barabasi Albert

sage: (graphs.RandomBarabasiAlbert(7,3)).show(figsize=[4,4], graph_border=True)

barabasi.png

Random GNM

sage: (graphs.RandomGNM(7,16)).show(figsize=[4,4], graph_border=True)

gnm.png

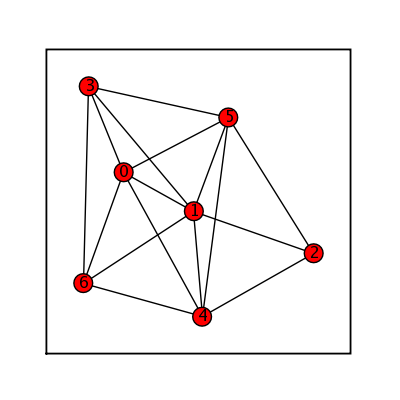
Random Newman Watts Strogatz

sage: (graphs.RandomNewmanWattsStrogatz(7,3,.5)).show(figsize=[4,4], graph_border=True)

newman.png

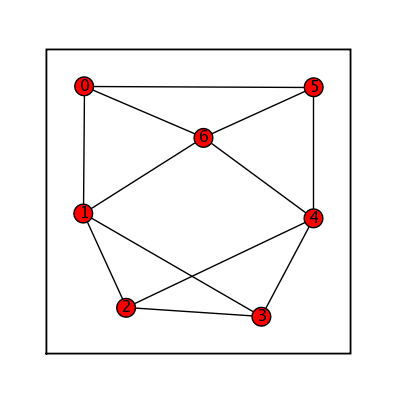
Random Holme Kim

sage: (graphs.RandomHolmeKim(12,3,.4)).show(figsize=[4,4], graph_border=True)

holme.png

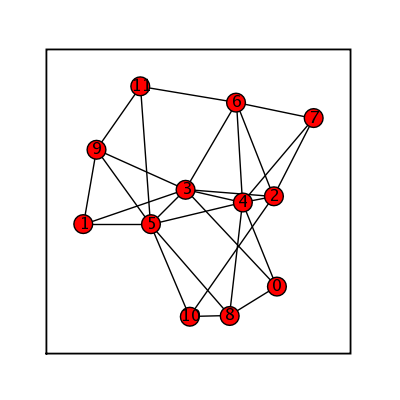
Random Lobster

sage: (graphs.RandomHolmeKim(12,3,.4)).show(figsize=[4,4], graph_border=True)

lobster.png

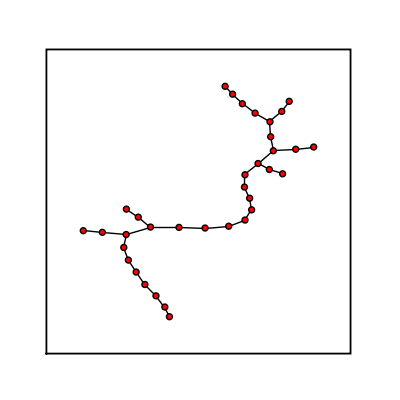
Random Tree Powerlaw

sage: (graphs.RandomTreePowerlaw(15)).show(figsize=[4,4], graph_border=True)

powerlaw.png

Random Regular

sage: (graphs.RandomRegular(3,20)).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)

randreg.png

Random Shell

sage: (graphs.RandomShell([(10,20,0.8),(20,40,0.8)])).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)

shell.png

Random Directed Graphs

Random Directed GN

sage: (graphs.RandomDirectedGN(12)).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)

randdirgn.png

Random Directed GNC

sage: (graphs.RandomDirectedGNC(12)).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)

randdirgnc.png

Random Directed GNR

sage: (graphs.RandomDirectedGNR(12,.15)).show(node_size=20, vertex_labels=False, figsize=[4,4], graph_border=True)

randdirgnr.png

Graphs With a Given Degree Sequence

Degree Sequence

sage: (graphs.DegreeSequence([3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3])).show(vertex_labels=False, node_size=30, figsize=[4,4], graph_border=True)

degseq.png

Degree Sequence Configuration Model

sage: (graphs.DegreeSequenceConfigurationModel([3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3,3])).show(vertex_labels=False, node_size=30, figsize=[4,4], graph_border=True)

degseqconf.png

Degree Sequence Tree

sage: (graphs.DegreeSequenceTree([3,1,3,3,1,1,1,2,1])).show(figsize=[4,4], graph_border=True)

degseqtree.png

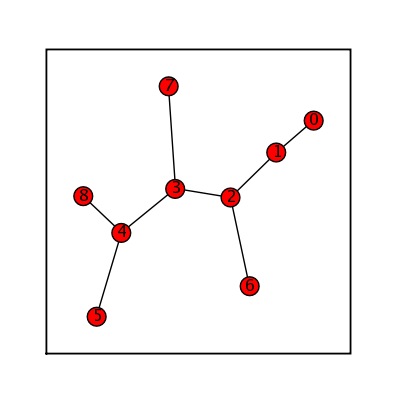
Degree Sequence Expected

sage: (graphs.DegreeSequenceExpected([1,2,3,2,3])).show(figsize=[4,4],graph_border=True)

degseqexp.png

graph_generators (last edited 2008-11-14 13:41:50 by anonymous)