|
Size: 21214
Comment:
|
← Revision 128 as of 2009-11-29 06:48:46 ⇥
Size: 3792
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| <<TableOfContents>> The SAGE Graph Theory Project |
|
| Line 2: | Line 6: |
| . We are implementing graph objects and algorithms in [[SAGE]]. The main people working on this project are Emily Kirkman and Robert Miller. | |
| Line 3: | Line 8: |
| The SAGE Graph Theory Project aims to implement Graph objects and algorithms in ["SAGE"]. | == Current Status == * NetworkX base classes have been interfaced, and all functions are soon to follow. * Jason Grout's (Brigham Young) SQL lite graph database is almost finished, and when it is done, it will be interfaced by Emily. * Jim Morrow (UW) has expressed interest in using SAGE for his [[http://www.math.washington.edu/~morrow/reu07/reu.html|summer REU]] on graphs. Robert is working on implementing electrical networks, which includes implementing edge weights and graphs with boundary. * Chris Godsil (Waterloo) has expressed interest in helping design a more general discrete math package in SAGE. * Brendan !McKay's isomorphism algorithm has been replicated for the open source community (it is called "nice", as opposed to "nauty"). * Graph plotting has been implemented in two dimensions: |
| Line 5: | Line 16: |
| The main people working on this project are Emily Kirkman and Robert Miller. | {{{ C = graphs.CubeGraph(9) color = {} for v in C.vertices(): b = v.count('1')/9 g = 1 - b if (0, g, b) in color: color[(0, g, b)].append(v) else: color[(0, g, b)] = [v] C.show(vertex_labels=False, node_size=60, graph_border=True, color_dict=color, figsize=[9,8]) }}} |
| Line 7: | Line 27: |
| == Survey of existing Graph Theory software == | {{attachment:9_cube.png}} |
| Line 9: | Line 29: |
| A. Software included with SAGE I. GAP I. Maxima I. Singular I. PARI, MWRANK, NTL I. Matplotlib I. GSL, Numeric |
== Talks == * On Oct. 20, 2006, Robert gave a [[http://sage.math.washington.edu/home/rlmill/talk_2001-10-20/2006-10-20SAGE.pdf|talk]] about the state of affairs for existing software which shared a few benchmarks and discussed some implementation ideas. * On Feb. 15, 2007, Robert and Emily gave an Informal Introduction to the Graph Theory Package. This talk was essentially a review of newly available features. * On Feb. 17, 2007, Robert gave a [[http://www.robertlmiller.com/talks/graph_intro.pdf|talk]] at Sage Days 3. * On Mar. 2, 2007, Robert gave a talk entitled "Opening Graph Automorphisms". * On Mar. 29, 2007, he followed up with a [[http://www.robertlmiller.com/talks/nauty.pdf|part two]] of this talk, after implementing "nice". * On Apr. 21, 2007, Emily presented a [[http://sage.math.washington.edu/home/ekirkman/talks/ECCAD.ppt|poster (ppt)]] introducing the SAGE graph theory package at East Coast Computer Algebra Day. * On Apr. 27, 2007, Emily gave a [[http://sage.math.washington.edu/home/ekirkman/talks/2007_04_27.html|talk]] introducing the (almost complete) sqlite database. |
| Line 17: | Line 38: |
| A. Software SAGE interfaces with (but does not include) | == Other wiki pages == * Surveys . [[http://wiki.sagemath.org/graph_survey|Existing Software]]: We are always seeking additions and comments. . [[http://wiki.sagemath.org/graph_db_survey|Existing Databases]]: Includes comments by Jason Grout. |
| Line 19: | Line 43: |
| I. [http://magma.maths.usyd.edu.au/magma/htmlhelp/text1452.htm Magma] 1. '''Representation''' . Sparse support; function computes memory requirement for graph with n verts and m edges; consists of graph itself, vertex set, and edge set 1. '''Storage/Pipes''' . one function opens either file or stream, files stored in [http://cs.anu.edu.au/~bdm/data/formats.html Graph6 and Sparse6 format] 1. '''Construction''' . From matrix; from edge tuples; from vertex neighbors; from edges of other graphs; subgraphs; quotient graphs; incremental construction; complement; contraction; breaking edges; line graph; switch nbrs for non-nbrs of a vertex; disjoint unions, edge unions; complete unions; cartesian, lexicographic and tensor products; n-th power (same vert set, incident iff dist $\leq$ n); graph $\leftrightarrow$ digraph; Cayley graph constructor; Schreier graph constructor; Orbital graph constructor; Closure graph constructor (given G, add edges to make G invariant under a given permutation group); Paley graphs and tournaments; graphs from incidence structures; converse(reverse digraph); n-th odd graph; n-th triangular graph; n-th square lattice graph; Clebsch, Shrikhande, Gewirtz and Chang graphs; 1. '''Decorations''' (Coloring, Weight, Flow, etc.) . Vertices have labels only; Edges have labels, capacity(non-negative integers, loops=0) and weights(totally ordered ring); 1. '''Invariants''' . #verts, #edges; characteristic polynomial; spectrum 1. '''Predicates''' . 2 verts incident, 2 edges incident, 1 vertex and 1 edge incident, subgraph, bipartite, complete, Eulerian, tree, forest, empty, null, path, polygon, regular 1. '''Subgraphs and Subsets''' . has k-clique, clique number, all cliques, maximum clique ([http://magma.maths.usyd.edu.au/magma/htmlhelp/text1473.htm "When comparing both algorithms in the situation where the problem is to find a maximum clique one observes that in general BranchAndBound does better. However Dynamic outperforms BranchAndBound when the graphs under consideration are large (more then 400 vertices) random graphs with high density (larger than 0.5%). So far, it can only be said that the comparative behaviour of both algorithms is highly dependent on the structure of the graphs."]), independent sets and number, 1. '''Adjacency, etc.''' . (in- & out-) degree, degree vector, valence (if regular), vertex nbrs, edge nbrs, bipartition, dominating sets 1. '''Connectivity''' . (strongly) connected, components, separable, 2-connected, 2-components, triconnectivity ([http://magma.maths.usyd.edu.au/magma/htmlhelp/text1466.htm "The linear-time triconnectivity algorithm by Hopcroft and Tarjan (HT73) has been implemented with corrections of our own and from C. Gutwenger and P. Mutzel (GM01). This algorithm requires that the graph has a sparse representation."]), k-vertex connectivity, vertex separator, k-edge connectivity, edge separator 1. '''Paths, etc.''' . distance and geodesic, diameter and corr. path, ball and sphere, distance partition, equitable partition, girth and corr. cycle 1. '''Trees, etc.''' . spanning tree, breadth first and depth first searches, rooted, root, parent, vertex paths 1. '''Colorings'''(see also Decorations) . chromatic number and index, optimal vertex and edge colorings, chromatic polynomial 1. '''Optimization''' . Max flow min cut (2 algorithms: [http://magma.maths.usyd.edu.au/magma/htmlhelp/text1499.htm#15274 Dinic & push-relabel]), maximum matching for bipartite, 1. '''Embedding''' (Planar graphs, etc.) . planarity, Kuratowski subgraphs, faces of a planar graph, embedding info as orientation of edges from a vertex 1. '''Algebra''' . adjacency matrix, distance matrix, incidence matrix, intersection matrix 1. '''Morphisms/Group Actions''' . interfaces ''nauty'' 1. '''Symmetry''' . vertex, edge and distance transitivity; orbit partitions; primitivity; symmetric; distance regularity and intersection array 1. '''Geometry''' . Go back and forth between incidence and coset geometries and their graphs; finite planes; 1. '''Generation/Random Graphs''' . interfaces ''nauty'' 1. '''Database''' . database interface, strongly regular graph DB, random graph from DB, slick implementation of for loops ("for G in D do ... end for;") |
* [[http://wiki.sagemath.org/graph_benchmark|Benchmarks]] . Initial Benchmarks indicated that NetworkX was the appropriate package for inclusion in SAGE. They were designed to compare the constructions and very basic functionality found in our survey of existing software. |
| Line 61: | Line 46: |
| I. Maple: '''networks''' package, which includes: 1. '''Representation''' . ? 1. '''Construction''' . new (0 verts), void (n verts, 0 edges), incremental construction, complement, complete, contraction, hypercubes, cycle, petersen, cube, icosahedron, dodecahedron, octahedron, tetrahedron, simplify a multigraph, union, subgraphs, 1. '''Decorations''' (Coloring, Weight, Flow, etc.) . vertex weights default to 0, edge weights default to 1 (can be any valid maple expression) 1. '''Invariants''' . characteristic polynomial 1. '''Adjacency, etc.''' . in-nbrs(arrivals), out-nbrs(departures), degree sequence, endpoints, graphical ("tests whether intlist is the degree sequence of a simple graph"), edge-nbrs, vert-nbrs, in-degree, out-degree, max & min degree, edge span & span polynomial ("The span polynomial in variable p gives the probability that G is spanning when each edge operates with probability p.", "When G is connected, this is the all-terminal reliability polynomial of G, and gives the probability that G is connected when each edge operates independently with probability p."), 1. '''Connectivity''' . components, edge-connectivity, 2-components, count minimal cutsets, rank ("The rank of an edgeset e is the number of vertices of G minus the number of components of the subgraph induced by e."), Whitney rank polynomial ("The rank polynomial is a sum over all subgraphs H of G of $x^{(rank(G) - rank(H))} y^{corank(H)}$."), 1. '''Paths, etc.''' . diameter, fundcyc ("Given a subset e of edges forming a unicyclic subgraph of a graph G, the edges forming the unique cycle are returned as a set. It is assumed that only one cycle is present."), girth, find path from a to b, 1. '''Trees, etc.''' . ancestor, daughter, count spanning trees (Kirchoff Matrix-Tree theorem), cycle base ("A spanning tree is found, and fundcyc() is then used to find all fundamental cycles with respect to this tree. They are returned as a set of cycles with each cycle being represented by a set of edges."), edge disjoint spanning tree, shortest path spanning tree, min weight spanning tree, Tutte polynomial ("The Tutte polynomial is a sum over all maximal forests H of G of $t^{ia(H)} z^{ea(H)}$ where $ia(H)$ is the internal activity of H and $ea(H)$ is the external activity of H.") 1. '''Colorings''' . chromatic polynomial, 1. '''Optimization''' . maximum flow (flow), Dinic algorithm for max flow (see Magma), flow polynomial ("The flow polynomial in variable h gives the number of nowhere-zero flows on G with edge labels chosen from integers modulo h."), minimum cut, 1. '''Embedding''' (Planar graphs, etc.) . isplanar, 1. '''Algebra''' . acycpoly ("The acyclicity polynomial in variable p gives the probability that G is acyclic when each edge operates with probability p."), adjacency matrix, distance table (allpairs- optional table gives shortest path trees, rooted at each vertex), incidence matrix, 1. '''Generation/Random Graphs''' . random graphs- specify #verts and prob of edge occuring, or #verts and #edges 1. '''Database''' . show command shows a table of known information about a network 1. '''Visualization''' . plots graphs either in lines (Linear) or in concentric circles (Concentric), ability to give specific graphs specific plotting procedures, 3d plots ("The location of the vertices of the graph is determined as follows. Let A be the adjacency matrix of G and let u, v and w be three eigenvectors of A with corresponding second, third, and fourth largest eigenvalue in absolute value. Then the (x,y,z) coordinates of the ith vertex of G is (u[i],v[i],w[i])."; "Sometimes other symmetries in the graph can be seen by using other eigenvectors. If the optional argument eigenvectors = [e1, e2, e3] is specified, where e1, e2, and e3 are vertex numbers (integers from 1 through the number of vertices), the eigenvectors corresponding to the eigenvalues of these relative magnitudes are used.") |
* [[http://wiki.sagemath.org/graph_plotting|Plotting]] * 2D plotting is implemented using matplotlib. * 3D plotting via Tachyon is coming soon. * 3D interactive viewing is on its way, via Java applets (pending some serious implementation issues). |
| Line 93: | Line 51: |
| I. Mathematica: [http://documents.wolfram.com/mathematica/Built-inFunctions/AdvancedDocumentation/DiscreteMath/GraphPlot/ GraphPlot] ([http://documents.wolfram.com/mathematica/Built-inFunctions/AdvancedDocumentation/DiscreteMath/GraphPlot/AdvancedDocumentationGraphPlotReferences.html biblio]) is built-in: also a few functions for "applications" (?); designed to work well with large graphs; also supports graphs from ''Combinatorica'' 1. '''Representation''' . graph simply ''is'' an adjacency matrix (could be sparse), or a list of rules (e.g. {1->2, 2->3, 3->4, 4->1}) 1. '''Construction''' . N/A (see representation) 1. '''Predicates''' . vertex list (apparently only nontrivial when graph is a rule list, see representation) 1. '''Subgraphs and Subsets''' . maximal independent vertex sets and edge sets, 1. '''Connectivity''' . list strongly connected components, 1. '''Paths, etc.''' . distance, pseudo-diameter (see [http://documents.wolfram.com/mathematica/Built-inFunctions/AdvancedDocumentation/DiscreteMath/GraphPlot/AdvancedDocumentationGraphPlotPseudoDiameter.html Documentation]) 1. '''Trees, etc.''' . [http://documents.wolfram.com/mathematica/Built-inFunctions/AdvancedDocumentation/DiscreteMath/GraphPlot/AdvancedDocumentationGraphPlotTreePlot.html TreePlot] uses the layered drawing algorithm, implements more control: 1. '''Optimization''' . maximum matching for bipartite, [http://documents.wolfram.com/mathematica/Built-inFunctions/AdvancedDocumentation/DiscreteMath/GraphPlot/AdvancedDocumentationGraphPlotMinCut.html min cut] problem 1. '''Visualization''' . [http://documents.wolfram.com/mathematica/Built-inFunctions/AdvancedDocumentation/DiscreteMath/GraphPlot/AdvancedDocumentationGraphPlotGraphPlotAndGraphPlot3D.html ALGORITHMS] include spring model, spring-electrical model, high-dimensional embedding (random seeds can be given for spring models, link includes options for the spring models); tree algorithms include radial drawing, layered drawing (see G. Di Battista, P. Eades, R. Tamassia, and I. G. Tollis, Algorithms for the Visualization of Graphs, Prentice-Hall, 1999.); vertex styles and colors, edge styles and colors; function to return coordinates without drawing |
* [[http://wiki.sagemath.org/graph_generators|Graph Generators]] * So far: Basic graph structures with intuitive graphics. * Extensive educational docstrings and many graph constructors. * Native positionings allow standard layouts and quicker plotting |
| Line 113: | Line 56: |
| A. Extensions of software that SAGE interfaces with I. Magma I. Maple a. [http://www.math.uga.edu/~mbaker/REU/maple/laplacian-guide.html 'laplacian.mpl']; [http://www.fmf.uni-lj.si/~mohar/Papers/Spec.pdf here] is a paper on the Laplacian Spectrum 1. '''Storage/Pipes''' . creation of certain spreadsheets, such as known eigenvalues and eigenvalues of increasing subdivisions of the graph 1. '''Construction''' . banana graphs, star graphs, bouquets and flowers, hypercubes, supercirc (see docs), subdivide edges into n edges, contract, assign directions (apparently in a random way) 1. '''Decorations''' (Coloring, Weight, Flow, etc.) . normalilze (so sum of weights = 1) 1. '''Algebra''' . discrete laplacian matrix (this function may fight with the built-in laplacian in 'linalg'), compute its eigenvalues given a measure, 1. '''Topology''' . (laplacian matrix), effective resistance between vertices, discrete and continuous canonical measure [http://www.math.uga.edu/~mbaker/REU/tex/canonical.pdf#search=%22graph%20tau%22 an unrelated explanation?] and tau (also, taushorten "Investigates the behavior of tau as an edge is shortened"), discrete dx measure a. [http://www.cecm.sfu.ca/CAG/papers/GTpaper.pdf GraphTheory] and [http://www.cecm.sfu.ca/CAG/papers/GT2006.pdf Part II] of the paper (haven't yet found the actual package...) I. Mathematica a. [http://www.combinatorica.com/ Combinatorica] - for a list of functions, see [http://www.cs.sunysb.edu/~skiena/combinatorica/help.pdf help.pdf], page 13-14, 18, 21, 23, 25 - for a [http://www.amazon.com/exec/obidos/ASIN/0521806860/ref=nosim/thealgorithmrepo/ book] |
* [[http://wiki.sagemath.org/graph_database|Database]] . Emily has provided a provisional database of graphs on up to seven vertices: |
| Line 131: | Line 59: |
| A. Software that SAGE can now include as is (not as an optional package...) I. [http://gato.sourceforge.net/ Gato], a tool that animates algorithms, perhaps SAGE cannot actually include right now as is, but license is LGPL, and it requires Python and Tcl/Tk . seems that you can write your algorithm in one window and watch it go, supports 3d I. [https://networkx.lanl.gov/ NetworkX], seems pretty comprehensive, released under "GNU Lesser General Public License", works on Python $\geq$ 2.3, interfaces with Matplotlib, Pygraphviz, Graphviz, Pydot, numpy or Numeric, Ipython, SciPy, PyGSL, sAsync, PyYAML 1. '''Representation''' * in Graph and DiGraph, "data structures based on an adjacency list implemented as a node-centric dictionary of dictionaries. The dictionary contains keys corresponding to the nodes and the values are dictionaries of neighboring node keys with the value None (the Python None type). This allows fast addition, deletion and lookup of nodes and neighbors in large graphs" * "The XGraph and XDiGraph classes are extensions of the Graph and DiGraph classes in base.py. The key difference is that an XGraph edge is a 3-tuple e=(n1,n2,x), representing an undirected edge between nodes n1 and n2 that is decorated with the object x. Here n1 and n2 are (hashable) node objects and x is a (not necessarily hashable) edge object. Since the edge is undirected, edge (n1,n2,x) is equivalent to edge (n2,n1,x). An XDiGraph edge is a similar 3-tuple e=(n1,n2,x), with the additional property of directedness. I.e. e=(n1,n2,x) is a directed edge from n1 to n2 decorated with the object x, and is not equivalent to the edge (n2,n1,x). Whether a graph or digraph allow self-loops or multiple edges is determined at the time of object instantiation via specifying the parameters selfloops=True/False and multiedges=True/False." 1. '''Storage/Pipes''' 1. '''Construction''' 1. '''Decorations''' (Coloring, Weight, Flow, etc.) 1. '''Invariants''' 1. '''Predicates''' 1. '''Subgraphs and Subsets''' 1. '''Adjacency, etc.''' 1. '''Connectivity''' 1. '''Paths, etc.''' 1. '''Trees, etc.''' 1. '''Colorings''' 1. '''Optimization''' 1. '''Embedding''' (Planar graphs, etc.) 1. '''Algebra''' 1. '''Morphisms/Group Actions''' 1. '''Symmetry''' 1. '''Geometry''' 1. '''Topology''' 1. '''Generation/Random Graphs''' 1. '''Database''' 1. '''Visualization''' A. Software that SAGE should include (or maybe interface with, or include as optional), pending stuff (e.g. licensing) I. [http://cs.anu.edu.au/~bdm/nauty/ Nauty] a. Benchmark program a. Source posted, but no public license - should contact Brendan !McKay a. Written in portable subset of C, python wrapper already in existence (see pynauty) a. Nauty interfaces with MAGMA and GRAPE (GAP package) 1. '''Construction''' includes gtools - quick generators for non-isomorphic graphs, also generates bipartite graphs and digraphs 1. '''Invariants''' canonical labelling 1. '''Morphisms/Group Actions''' Computing automorphism groups of graphs and digraphs, isomorphism testing I. [http://www.graphviz.org GraphViz] a. open source, Common Public License Version 1.0 a. poorly documented, at least on the web 1. '''Visualization''' DOT makes "hierarchical" drawings of directed graphs. Algorithm aims edges in same direction and attempts to not cross edges and reduce length. NEATO uses spring method, via the Kamada-Kawai algorithm (statistical multi-dimensional scaling) fdp also uses the spring model, via the Fruchterman-Reingold heuristic (handles larger graphs and undirected, clustered graphs) I. [http://cs.anu.edu.au/people/bdm/plantri/ plantri and fullgen] written in C, tested mainly on UNIX, weird license ('free for all purposes other than sale for profit. However, they remain subject to our copyright and are not "public domain".'): interesting note, co-authored by Brendan !McKay, of ''nauty'' 1. '''Generation/Random Graphs''' * plantri: "exactly one member of each isomorphism class is output without the need for storing them. The speed of generation is more than 100,000 graphs per second in most cases, so extremely large classes of graph can be exhaustively listed.", classes include planar triangulations, quadrangulations, simple graphs, triangulations of a disc, planar cubic and quartic graphs * fullgen generates fullerenes * see also [http://hep.physics.indiana.edu/~tsulanke/graphs/surftri/ surftri], which generates triangulations of surfaces of higher genus A. Software that is incompatible with SAGE but still useful (e.g. web-based applets) I. [http://www.geocities.com/pechv_ru/ GRIN] a. for windows only a. not open-source, but free download 1. '''Connectivity''' bridges and cutpoints 1. '''Paths, etc.''' Paths and Cycles (Eulerian and Hamiltonian), Shortest Paths, Max Capacity Path, K Shortest paths, Critical path 1. '''Trees, etc.''' Minimal spanning tree 1. '''Optimization''' Max Flow 1. '''Morphisms/Group Actions''' Automorphism group 1. '''Topology''' Metrics of the graph Density, Undensity and so on...) 1. '''Visualization''' 2d only, Clipboard edit, decomposition of edges, resize I. [http://prolland.free.fr/works/research/dsatphp/dsat.html DSATUR], a program for computing graph colorings, algorithm [http://prolland.free.fr/works/research/dsat/index.html#anchor38034 documentation] in French, input in [http://mat.gsia.cmu.edu/COLOR/general/ccformat.ps DIMACS] format, [http://prolland.free.fr/works/research/dsatphp/dsat.txt source code] A. Algorithm descriptions for specific problems I. [http://rtm.science.unitn.it/intertools/ InterTools] 1. Maximum Clique in Graphs (MAX-CLIQUE) 1. Graph Partitioning (equicut) 1. Quadratic Assignment Problem (QAP) A. Apparently useless / and/or misc. / and/or etc. I. [http://www.npac.syr.edu/NPAC1/PUB/ranka/part/part.html Scalable Libraries for Graph Partitioning], no software yet, but good references on page: "Efficient methods for graph partitioning and incremental graph partitioning are important for parallelization of a large number of unstructured and/or adaptive applications." == Functionality categories == 1. '''Representation''' 1. '''Storage/Pipes''' 1. '''Construction''' 1. '''Decorations''' (Coloring, Weight, Flow, etc.) 1. '''Invariants''' 1. '''Predicates''' 1. '''Subgraphs and Subsets''' 1. '''Adjacency, etc.''' 1. '''Connectivity''' 1. '''Paths, etc.''' 1. '''Trees, etc.''' 1. '''Colorings''' 1. '''Optimization''' 1. '''Embedding''' (Planar graphs, etc.) 1. '''Algebra''' 1. '''Morphisms/Group Actions''' 1. '''Symmetry''' 1. '''Geometry''' 1. '''Topology''' 1. '''Generation/Random Graphs''' 1. '''Database''' 1. '''Visualization''' |
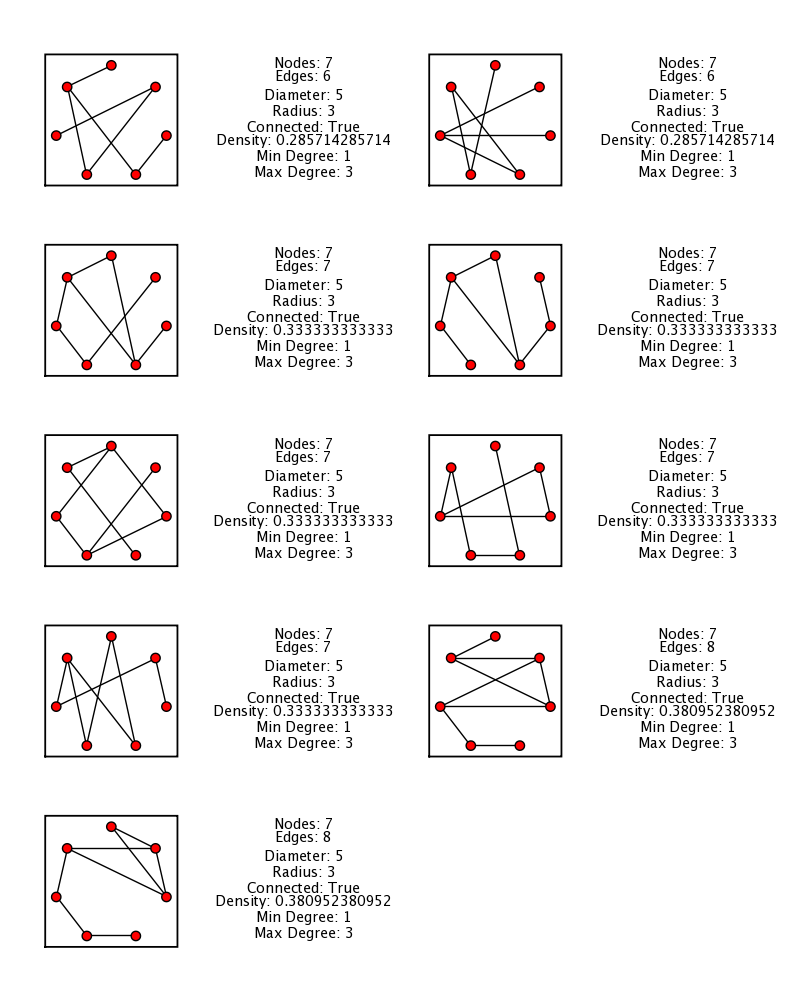
{{{ graphs_query.show_graphs(with_properties=True, nodes=7, diameter=5) }}} {{attachment:database.png}} |
Contents
The SAGE Graph Theory Project
Introduction
We are implementing graph objects and algorithms in SAGE. The main people working on this project are Emily Kirkman and Robert Miller.
Current Status
- NetworkX base classes have been interfaced, and all functions are soon to follow.
- Jason Grout's (Brigham Young) SQL lite graph database is almost finished, and when it is done, it will be interfaced by Emily.
Jim Morrow (UW) has expressed interest in using SAGE for his summer REU on graphs. Robert is working on implementing electrical networks, which includes implementing edge weights and graphs with boundary.
- Chris Godsil (Waterloo) has expressed interest in helping design a more general discrete math package in SAGE.
Brendan McKay's isomorphism algorithm has been replicated for the open source community (it is called "nice", as opposed to "nauty").
- Graph plotting has been implemented in two dimensions:
C = graphs.CubeGraph(9)
color = {}
for v in C.vertices():
b = v.count('1')/9
g = 1 - b
if (0, g, b) in color: color[(0, g, b)].append(v)
else: color[(0, g, b)] = [v]
C.show(vertex_labels=False, node_size=60, graph_border=True, color_dict=color, figsize=[9,8])
Talks
On Oct. 20, 2006, Robert gave a talk about the state of affairs for existing software which shared a few benchmarks and discussed some implementation ideas.
- On Feb. 15, 2007, Robert and Emily gave an Informal Introduction to the Graph Theory Package. This talk was essentially a review of newly available features.
On Feb. 17, 2007, Robert gave a talk at Sage Days 3.
- On Mar. 2, 2007, Robert gave a talk entitled "Opening Graph Automorphisms".
On Mar. 29, 2007, he followed up with a part two of this talk, after implementing "nice".
On Apr. 21, 2007, Emily presented a poster (ppt) introducing the SAGE graph theory package at East Coast Computer Algebra Day.
On Apr. 27, 2007, Emily gave a talk introducing the (almost complete) sqlite database.
Other wiki pages
- Surveys
Existing Software: We are always seeking additions and comments.
Existing Databases: Includes comments by Jason Grout.
- Initial Benchmarks indicated that NetworkX was the appropriate package for inclusion in SAGE. They were designed to compare the constructions and very basic functionality found in our survey of existing software.
- 2D plotting is implemented using matplotlib.
- 3D plotting via Tachyon is coming soon.
- 3D interactive viewing is on its way, via Java applets (pending some serious implementation issues).
- So far: Basic graph structures with intuitive graphics.
- Extensive educational docstrings and many graph constructors.
- Native positionings allow standard layouts and quicker plotting
- Emily has provided a provisional database of graphs on up to seven vertices:
graphs_query.show_graphs(with_properties=True, nodes=7, diameter=5)