|
Size: 8725
Comment:
|
← Revision 45 as of 2009-06-27 14:41:17 ⇥
Size: 9285
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 79: | Line 79: |
| Line 103: | Line 104: |
| patch available at [[http://trac.sagemath.org/sage_trac/ticket/5133|issue 5133]] on trac | |
| Line 146: | Line 148: |
| Rewrite LinBox wrappers using C++ wrappers of Cython directly | * Change LinBox wrappers -> new spkg * New classes `matrix_modn_dense_double`, `matrix_modn_dense_float` [[http://sage.math.washington.edu/home/burcin/linbox_interface.patch|patch available on sage.math]] * bindings still under construction Timings: Multiplying 3000x3000 matrices over GF(101) * Sage proper implementation (default): 30.24s * Old LinBox wrappers (using double): 5.93s * New LinBox wrappers: (using double): 5.3s * New LinBox wrappers: (using float 3.52s |
Sage Days 16 Project Idea Page
Create a Cython class for points on elliptic curves and optimize basic arithmetic
PEOPLE: William Stein, wouter, dkohel
- Right now basic arithmetic on elliptic curves is way too slow. It could be sped up by moving the point class to Cython, and possibly by using better formulas for arithmetic, e.g., using projective coordinates.
Create elliptic curve classes for elliptic curve models in the Explicit-Formulas Database
PEOPLE: David Kohel, Wouter Castryck
- In order to optimize and compare arithmetic, we should first implement alternative models and verify relative performance. The isomorphisms between different models should also be implemented, and classes for isogenies of these models developed, making use first of the new isogenies code, and eventually putting in place special optimized code for specific models.
(Wouter) As a comment to that, none of these alternative models cover the whole range of elliptic curves (as far as I know). E.g. an elliptic curve can be shaped into Edwards form only if it has a rational point of order 4. So one should in any case optimize arithmetic on pure Weierstrass curves (using weighted projective coordinates or so).
See the EFD: http://www.hyperelliptic.org/EFD/
Rewrite abelian groups (hard)
PEOPLE: William Stein, rlmiller, dkohel, wstein, dloeffler, bjarke
It would be possible to use trac 5882 to rewrite abelian groups natively in Sage (not using GAP), in a way that is much more flexible than the current implementation. This could be useful for many number theory applications.
- This project is "hard", since many have tried and always failed. The reason for this is the temptation to rewrite the current implementation all at once. See more details for the new plan, which avoids this pitfall...
Multisets
PEOPLE: dkohel, rlmiller, brian
Optimize/better document/generally improve graph theory library in Sage
PEOPLE: Robert Miller
Ticket #6085 contains a lot of work so that a graph created by Graph(implementation='c_graph') is just as functional as a Sage graph. I will be sporadically working on improving documentation and optimizing graphs all week, and anyone interested is welcome to join.
Cliquer SPKG for Sage
PEOPLE: Robert Miller, Nathann Cohen (remotely), brian, ncohen, rlmiller, bjarke
Take a look at the possibility of making GAP a dynamically loadable library
PEOPLE: Robert Miller, wstein
Robert Miller and William Stein succeeded in making a first very rough Cython module that links in GAP as a library and allows one to type commands to the interpreter. See http://trac.sagemath.org/sage_trac/ticket/6391/. This proof-of-concept that not only can GAP be linked as a library instead of used via pexpect, but that the result is likely to be *better* than libPARI and libSingular, in that one has full access to the GAP interpreter scripts and capabilities (just like embedding Python allows for that). Also, it turns out that so far there are no issues because of the GAP memory manager.
Python implementation of Ford-Fulkerson algorithm
PEOPLE: Robert Miller, brian, michael, tom
I plan on at least copying the Python implementation on wikipedia, since now we have nothing at all for max flow problems. Hopefully then someone who really cares about it will try to use it, realize it is slow, start improving it, etc. etc. etc.
There were several algorithms created - Edmonds-Karp (tom, michal), Push-Relabel (from wikipedia - brian - now optimizing the code), Dinic (tom - performs better on dense graph, needs? improvement), Malhotra, Pramodh Kumar, and Maheshwari's (MPM - michal - not yet finished) and some general framework (tom still? working on it)
Frobenius number and genus of numerical semigroups using toric Grobner bases
PEOPLE: Bjarke Hammersholt Roune
- I plan to code Frobenius number (largest gap) and genus (number of gaps) functions for numerical semigrups using two related algorithms based on toric ideals. These algorithms can handle random numerical semigroups generated by numbers with thousands of digits, as long as there are not too many minimal generators. I'm happy to explain either algorithm if you want to help or are just curious. The steps needed are these:
- Find the best way to compute toric Grobner bases in Sage (4ti2?)
- Improve the integration of the library Frobby for monomial ideal computations.
- Code the algorithms (should be easy at this point)
A Cython interface to Frobby was written and submitted to track along with an spkg. A preexisting command-line based interface to 4ti2 by Mike Hansen that was floating around was improved and submitted to trac. This allowed the easy implementation of the Frobenius number computation, while time ran out on coding the genus, though this should not be too hard to do.
PolyBoRi and Singular
PEOPLE: Martin Albrecht, Burcin Erocal
Both PolyBoRi's (Gröbner bases in GF(2)[x_i]/<x_i^2+x_i>) and Singular's interface need some (engineering) work & documentation.
Elliptic curves isogenies -- greatly improve usability
PEOPLE: William Stein, dkohel, wouter, rlmiller, hamish
Dan Shumow wrote new code for computing isogenies between elliptic curves, but it is still very rough around the edges. Fix it up. See e.g., http://trac.sagemath.org/sage_trac/ticket/6384
Siegel Theta Functions
PEOPLE: guardia, holuk, drkohel, rlmiller, preston, schulze-pillot
See http://trac.sagemath.org/sage_trac/ticket/6371 for code that calculates classical theta functions, their derivatives, and some related functions I'm interested in, to arbitrary precision.
Multimodular reconstruction implementation
PEOPLE: clement, wstein, burcin, rlmiller, dloeffler, sebastian, brian
- CRT in rings/arith.py is unsanely slow
MultimodularBasis class is broken
patch available at issue 5133 on trac
Fix / Unify code / optimize the hell out of it
Add the early termination technique for the reconstruction of multiple values Apply it to Burcin's computation of nullspace over Z[x]
PEOPLE: Burcin Erocal, Clément Pernet
Minpoly over small finite field
PEOPLE: clement, michael, brian, preston, emmanuel
#6296 Implement a certified computation of minpoly over a small finite field.
PEOPLE: Clément Pernet
Refactor symbolic functions
PEOPLE: burcin, wstein, tom
Merge the PrimitiveFunction and SFunction classes in sage.symbolic.function and make it easier to define new special functions with custom evaluation, printing, etc. methods. This also involves adding capability to represent symbolic sums and integrals in Sage as a first step to adding native Sage code to deal with these.
M4RI: improvement of PLUQ factorization
PEOPLE: Martin Albrecht, Clément Pernet
Change/improve the slow column swap in PLUQ factorization
- We improved the PLUQ/LQUP base case by using up to four tables now instead of only two.
- We improved the implementation for various column swaps and permutation matrix multiplications.
- We moved from PLUQ to LQUP because it requires less column swaps.


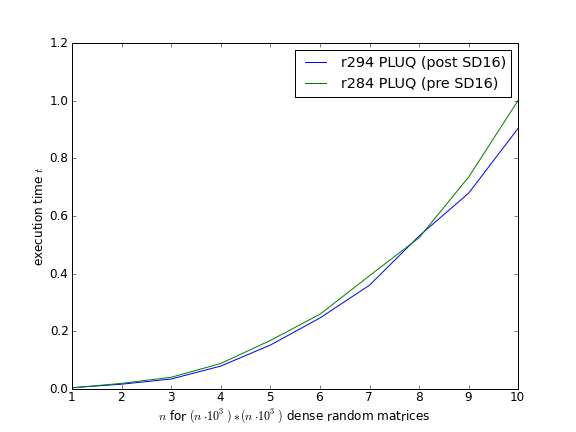
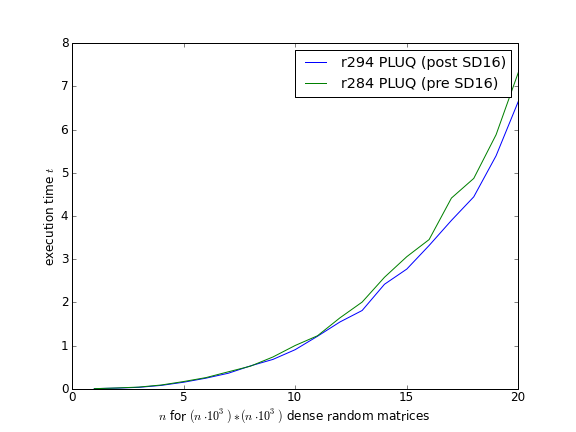
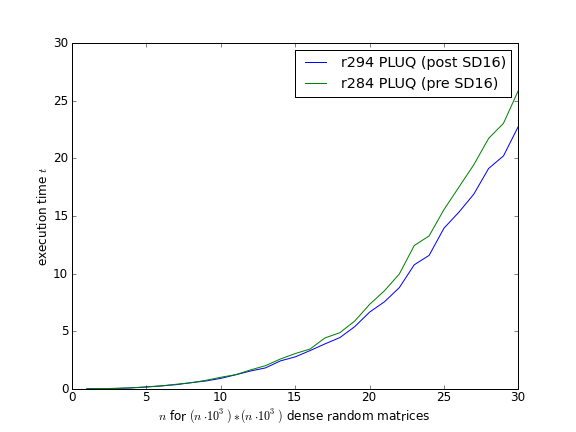
LinBox wrappers
Change LinBox wrappers -> new spkg
New classes matrix_modn_dense_double, matrix_modn_dense_float
- bindings still under construction
Timings: Multiplying 3000x3000 matrices over GF(101)
- Sage proper implementation (default): 30.24s
Old LinBox wrappers (using double): 5.93s
New LinBox wrappers: (using double): 5.3s
New LinBox wrappers: (using float 3.52s
PEOPLE: Burcin Erocal, Clément Pernet, rlmiller, malb
Ray class groups and Groessencharacters
Implement computations of the ray class group modulo an ideal of a number field, and the corresponding character group.
PEOPLE: David Loeffler, rlmiller, wstein, dkohel, haluk, michael
Pari 2.4 Upgrade
- PEOPLE: wstein, dloeffler, hamish, michael
Sage notebook security
- PEOPLE: Yoav, malb
- We had some nice design discussions.
Texmacs --> Sage Worksheet converter
- PEOPLE: Offray
SPD (simple python distro)
- PEOPLE Offray
