|
Size: 21592
Comment:
|
Size: 20759
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 11: | Line 11: |
=== The witch of Maria Agnesi === |
= Animated = == The witch of Maria Agnesi == |
| Line 158: | Line 158: |
| === The Towers of Hanoi === | == The Towers of Hanoi == |
| Line 215: | Line 215: |
| === Fibonacci Tiles === | == Fibonacci Tiles == |
| Line 230: | Line 230: |
| === Pencil of conics === | == Pencil of conics == |
| Line 259: | Line 259: |
| == Pictures drawn by Sage == | = Pictures drawn by Sage = |
| Line 263: | Line 263: |
| <<TableOfContents>> === Everywhere continuous, nowhere differentiable function === |
== Everywhere continuous, nowhere differentiable function == |
| Line 278: | Line 276: |
| === Mirrored balls in tachyon === | == Mirrored balls in tachyon == |
| Line 296: | Line 294: |
| === Math art by Tom Boothby === | == Math art by Tom Boothby == |
| Line 323: | Line 321: |
| === Twisted cubic in tachyon === | == Twisted cubic in tachyon == |
| Line 340: | Line 338: |
| === Reflections from four spheres in tachyon === | == Reflections from four spheres in tachyon == |
| Line 357: | Line 355: |
| === A cone inside a sphere === | == A cone inside a sphere == |
| Line 367: | Line 365: |
| === A cylinder inside a cone === | == A cylinder inside a cone == |
| Line 377: | Line 375: |
| === A hypotrochoid animation by Dean Moore === Hypotrochoid. Written by Dean Moore, February 2008 This animation was moved to the section on the animate command : [[http://wiki.sagemath.org/animate#AhypotrochoidanimationbyDeanMoore]] === A simpler hypotrochoid === This animation was moved to the section on the animate command : [[http://wiki.sagemath.org/animate#Asimplerhypotrochoid]] === The witch of Maria Agnesi === by Marshall Hampton This animation was moved to the section on the animate command : [[http://wiki.sagemath.org/animate#ThewitchofMariaAgnesi]] === p-adic Seasons Greetings === |
== p-adic Seasons Greetings == |
| Line 407: | Line 391: |
| === Lorentz butterfly === | == Lorentz butterfly == |
| Line 463: | Line 447: |
| === Feigenbaum diagram === | == Feigenbaum diagram == |
| Line 494: | Line 478: |
| === Sierpinski triangle === | == Sierpinski triangle == |
| Line 534: | Line 518: |
| === The Tamer and the Lion by Provencal and Labbe === This animation was moved to the section on the animate command : [[http://wiki.sagemath.org/animate#TheTamerandtheLionbyProvencalandLabbe]] === Integral Curvature Apollonian Circle Packing === |
== Integral Curvature Apollonian Circle Packing == |
| Line 617: | Line 597: |
| === Call graph of a recursive function === | == Call graph of a recursive function == |
see the attachments
This page contains animations drawn using Sage. One can create an animation (.gif) in Sage from a list of graphics objects using the animate command. Currently, to export an animation in .gif format, you might need to install the ImageMagick command line tools package (the convert command). See the documentation for more information:
sage: animate?
Contents
- Animated
-
Pictures drawn by Sage
- Everywhere continuous, nowhere differentiable function
- Mirrored balls in tachyon
- Math art by Tom Boothby
- Twisted cubic in tachyon
- Reflections from four spheres in tachyon
- A cone inside a sphere
- A cylinder inside a cone
- p-adic Seasons Greetings
- Lorentz butterfly
- Feigenbaum diagram
- Sierpinski triangle
- Integral Curvature Apollonian Circle Packing
- Call graph of a recursive function
Animated
The witch of Maria Agnesi
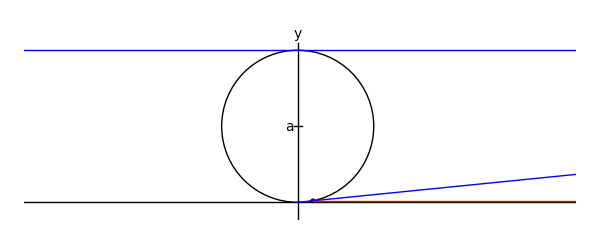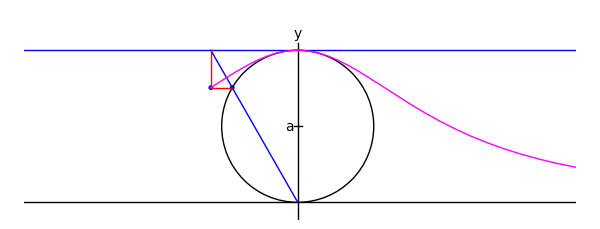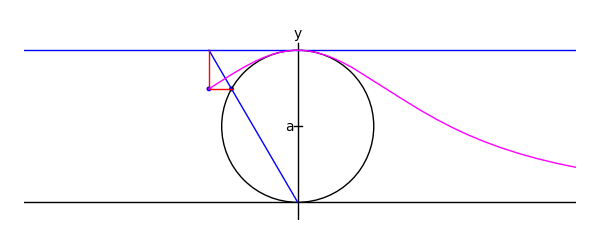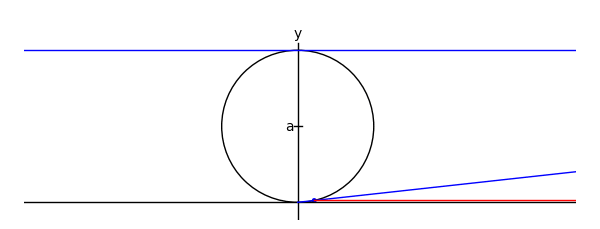
by Marshall Hampton
xtreme = 4.1
myaxes = line([[-xtreme,0],[xtreme,0]],rgbcolor = (0,0,0))
myaxes = myaxes + line([[0,-1],[0,2.1]],rgbcolor = (0,0,0))
a = 1.0
t = var('t')
npi = RDF(pi)
def agnesi(theta):
mac = circle((0,a),a,rgbcolor = (0,0,0))
maL = line([[-xtreme,2*a],[xtreme,2*a]])
maL2 = line([[0,0],[2*a*cot(theta),2*a]])
p1 = [2*a*cot(theta),2*a*sin(theta)^2]
p2 = [2*a*cot(theta)-cot(theta)*(2*a-2*a*sin(theta)^2),2*a*sin(theta)^2]
maL3 = line([p2,p1,[2*a*cot(theta),2*a]], rgbcolor = (1,0,0))
map1 = point(p1)
map2 = point(p2)
am = line([[-.05,a],[.05,a]], rgbcolor = (0,0,0))
at = text('a',[-.1,a], rgbcolor = (0,0,0))
yt = text('y',[0,2.2], rgbcolor = (0,0,0))
xt = text('x',[xtreme + .1,-.1], rgbcolor = (0,0,0))
matext = at+yt+xt
ma = mac+myaxes+maL+am+matext+maL2+map1+maL3+map2
return ma
def witchy(theta):
ma = agnesi(theta)
agplot = parametric_plot([2*a*cot(t),2*a*sin(t)^2],[t,.001,theta], rgbcolor = (1,0,1))
return ma+agplot
a2 = animate([witchy(i) for i in srange(.1,npi-.1,npi/60)]+[witchy(i) for i in srange(npi-.1,.1,-npi/60)], xmin = -3, xmax = 3, ymin = 0, ymax = 2.3, figsize = [6,2.3], axes = False)
a2.show()
A simpler hypotrochoid
The following animates a hypotrochoid
import operator
# The colors for various elements of the plot:
class color:
stylus = (1, 0, 0)
outer = (.8, .8, .8)
inner = (0, 0, 1)
plot = (0, 0, 0)
center = (0, 0, 0)
tip = (1, 0, 0)
# and the corresponding line weights:
class weight:
stylus = 1
outer = 1
inner = 1
plot = 1
center = 5
tip = 5
scale = 1 # The scale of the image
animation_delay = .1 # The delay between frames, in seconds
# Starting and ending t values
t_i = 0
t_f = 2*pi
# The t values of the animation frames
tvals = srange(t_i, t_f, (t_f-t_i)/60)
r_o = 8 # Outer circle radius
r_i = 2 # Inner circle radius
r_s = 3 # Stylus radius
# Coordinates of the center of the inner circle
x_c = lambda t: (r_o - r_i)*cos(t)
y_c = lambda t: (r_o - r_i)*sin(t)
# Parametric coordinates for the plot
x = lambda t: x_c(t) + r_s*cos(t*(r_o/r_i))
y = lambda t: y_c(t) - r_s*sin(t*(r_o/r_i))
# Maximum x and y values of the plot
x_max = r_o - r_i + r_s
y_max = find_maximum_on_interval(y, t_i, t_f)[0]
# The plots of the individual elements. Order is important; plots
# are stacked from bottom to top as they appear.
elements = (
# The outer circle
lambda t_f: circle((0, 0), r_o, rgbcolor=color.outer, thickness=weight.outer),
# The plot itself
lambda t_f: parametric_plot((x, y), t_i, t_f, rgbcolor=color.plot, thickness=weight.plot),
# The inner circle
lambda t_f: circle((x_c(t_f), y_c(t_f)), r_i, rgbcolor=color.inner, thickness=weight.inner),
# The inner circle's center
lambda t_f: point((x_c(t_f), y_c(t_f)), rgbcolor=color.center,pointsize=weight.center),
# The stylus
lambda t_f: line([(x_c(t_f), y_c(t_f)), (x(t_f), y(t_f))], rgbcolor=color.stylus, thickness=weight.stylus),
# The stylus' tip
lambda t_f: point((x_c(t_f), y_c(t_f)), rgbcolor=color.tip, pointsize=weight.tip),
)
# Create the plots and animate them. The animate function renders an
# animated gif from the frames provided as its first argument.
# Though avid python programmers will find the syntax clear, an
# explanation is provided for novices.
animation = animate([sum(f(t) for f in elements)
for t in tvals],
xmin=-x_max, xmax=x_max,
ymin=-y_max, ymax=y_max,
figsize=(x_max*scale, y_max*scale * y_max/x_max))
animation.show(delay=animation_delay)
# The previous could be expressed more pedagogically as follows:
#
# Evaluate each function in the elements array for the provided t
# value:
#
# plots = lambda t: f(t) for f in elements
#
# Join a group of plots together to form a single plot:
#
# def join_plots(plots):
# result = plots[0]
# for plot in plots[1:]:
# result += plot
# return result
#
# or
#
# join_plots = sum
#
# Create an array of plots, one for each provided t value:
#
# frames = [join_plots(plots(t)) for t in tvals]
#
# Finally, animate the frames:
#
# animation = animate(frames)
The Towers of Hanoi

by Pablo Angulo
def plot_towers(towers):
'''Returns a plot of the towers of Hanoi
Uses matrix_plot
'''
K=max(max(l) for l in towers if l)+1
M=matrix(ZZ,K,6*K+7)
#first tower
for t in range(len(towers[0])):
j = t
k=towers[0][t]-1
for l in range(K+1-k,K+2+k):
M[K-1-j,l]=1
#second tower
for t in range(len(towers[1])):
j = t
k=towers[1][t]-1
for l in range(3*K+3-k,3*K+4+k):
M[K-1-j,l]=1
#third tower
for t in range(len(towers[2])):
j = t
k=towers[2][t]-1
for l in range(5*K+5-k,5*K+6+k):
M[K-1-j,l]=1
return matrix_plot(M, axes=False)
def animate_towers(towers,a=0,b=1,c=2,k=-1):
'''Move last k discs from column a into column b
Assumes that the last k discs of column a are all smaller
than the discs in columns b and c
'''
if k==0: return
if k==-1: k=len(towers[a])
for t in animate_towers(towers,a,c,b,k-1):
yield t
disc = towers[a].pop()
towers[b].append(disc)
yield plot_towers(towers)
for t in animate_towers(towers,c,b,a,k-1):
yield t
towers = (range(4,0,-1),[],[])
initial = plot_towers(towers)
frame_list=[initial]+list(animate_towers(towers))
animate(frame_list, axes=False).show(delay=80)
Fibonacci Tiles

by Sébastien Labbé
sage: path_op = dict(rgbcolor='red', thickness=1)
sage: fill_op = dict(rgbcolor='blue', alpha=0.3)
sage: options = dict(pathoptions=path_op, filloptions=fill_op, endarrow=False, startpoint=False)
sage: G = [words.fibonacci_tile(i).plot(**options) for i in range(7)]
sage: a = animate(G)
sage: a.show(delay=150)
Pencil of conics
by Pablo Angulo 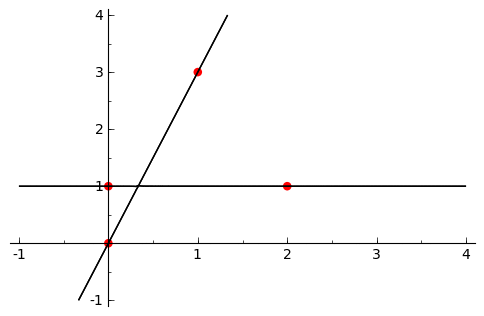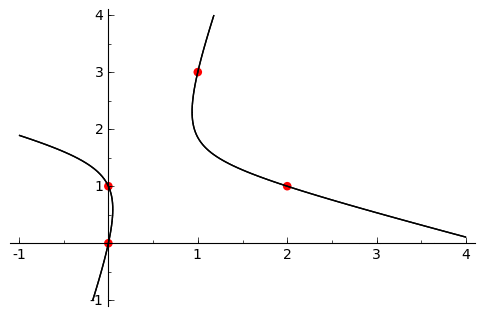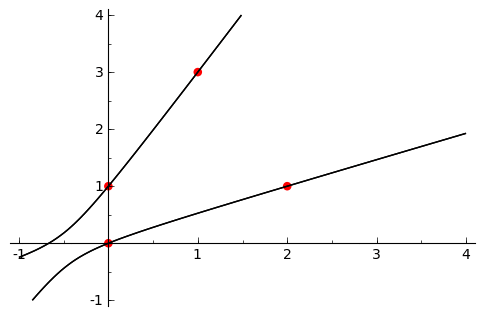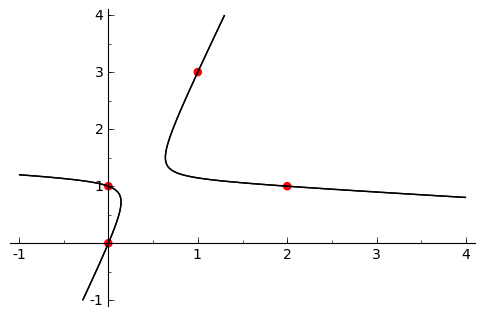
puntos = [(0,0),(0,1),(1,3),(2,1)]
K = len(puntos)
var('x y')
coefs = matrix(QQ, K, 6)
for j in range(K):
x0, y0 = puntos[j]
coefs[j,:] = vector([x0^2, y0^2, x0*y0, x0, y0, 1])
K = coefs.right_kernel()
v1 = K.basis()[0]
v2 = K.basis()[1]
graficas = []
for t in srange(0,2*pi,0.3):
c1, c2 = sin(t), cos(t)
a,b,c,d,e,f = c1*v1 + c2*v2
curva = a*x^2 + b*y^2 + c*x*y + d*x + e*y + f
graficas.append( point2d(puntos,color=(1,0,0),pointsize=30) +
implicit_plot(curva,(x,-1,4),(y,-1,4)) )
a = animate(graficas)
a.show(delay=10)
Pictures drawn by Sage
These pictures and images were drawn by Sage.
Everywhere continuous, nowhere differentiable function
- Everywhere continuous, nowhere differentiable function (in the infinite limit, anyway):
p = Graphics()
for n in range(1,20):
f = lambda x: sum([sin(x*3^i)/(2^i) for i in range(1,n)])
p += plot(f,0,float(pi/3),plot_points=2000,rgbcolor=hue(n/20))
p.show(xmin=0, ymin=0,dpi=250)

Mirrored balls in tachyon
t = Tachyon(camera_center=(8.5,5,5.5), look_at=(2,0,0), raydepth=6, xres=1500, yres=1500)
t.light((10,3,4), 1, (1,1,1))
t.texture('mirror', ambient=0.05, diffuse=0.05, specular=.9, opacity=0.9, color=(.8,.8,.8))
t.texture('grey', color=(.8,.8,.8), texfunc=7) ## try other values of texfunc too!
t.plane((0,0,0),(0,0,1),'grey')
t.sphere((4,-1,1), 1, 'mirror')
t.sphere((0,-1,1), 1, 'mirror')
t.sphere((2,-1,1), 0.5, 'mirror')
t.sphere((2,1,1), 0.5, 'mirror')
show(t)

Math art by Tom Boothby
# Author: Tom Boothby
# This is a remake of an old art piece I made in POVRay
t = Tachyon(xres=1000,yres=600, camera_center=(1,0,5), antialiasing=3)
t.light((4,3,2), 0.2, (1,1,1))
t.texture('t0', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(1.0,1,1))
t.texture('t1', ambient=0.5, diffuse=0.5, specular=0.0, opacity=1.0, color=(0,0,0))
t.texture('t2', ambient=0.2, diffuse=0.7, specular=0, opacity=0.7, color=(.5,.5,.5))
t.texture('t3', ambient=.9, diffuse=5, specular=0,opacity=.1, color=(1,0,0))
t.sphere((1,0,0), 30, 't2')
k=0
for i in srange(-pi*10,0,.01):
k += 1
t.sphere((cos(i/10)-.1, sin(i/10)*cos(i), sin(i/10)*sin(i)), 0.1, 't0')
t.sphere((cos(i/10) + 2.1, sin(i/10)*cos(i), sin(i/10)*sin(i)), 0.1, 't1')
t.show(verbose=1)

Twisted cubic in tachyon
t = Tachyon(xres=512,yres=512, camera_center=(5,0,0))
t.light((4,3,2), 0.2, (1,1,1))
t.texture('t0', ambient=0.1, diffuse=0.9, specular=0.5, opacity=1.0, color=(1.0,0,0))
t.texture('t1', ambient=0.1, diffuse=0.9, specular=0.3, opacity=1.0, color=(0,1.0,0))
t.texture('t2', ambient=0.2, diffuse=0.7, specular=0.5, opacity=0.7, color=(0,0,1.0))
k=0
for i in srange(-5,1.5,0.1):
k += 1
t.sphere((i,i^2-0.5,i^3), 0.1, 't%s'%(k%3))
t.show()

Reflections from four spheres in tachyon
t6 = Tachyon(camera_center=(0,-4,1), xres = 800, yres = 600, raydepth = 12, aspectratio=.75, antialiasing = True)
t6.light((0.02,0.012,0.001), 0.01, (1,0,0))
t6.light((0,0,10), 0.01, (0,0,1))
t6.texture('s', color = (.8,1,1), opacity = .9, specular = .95, diffuse = .3, ambient = 0.05)
t6.texture('p', color = (0,0,1), opacity = 1, specular = .2)
t6.sphere((-1,-.57735,-0.7071),1,'s')
t6.sphere((1,-.57735,-0.7071),1,'s')
t6.sphere((0,1.15465,-0.7071),1,'s')
t6.sphere((0,0,0.9259),1,'s')
t6.plane((0,0,-1.9259),(0,0,1),'p')
t6.show()
A cone inside a sphere
sage: u,v = var("u,v")
sage: p1 = parametric_plot3d([cos(u)*v, sin(u)*v, 3*v/2-1/3], (u, 0, 2*pi), (v, 0, 0.95),plot_points=[20,20])
sage: p2 = sphere((0,0,2/3), color='red', opacity=0.5, aspect_ratio=[1,1,1])
sage: show(p1+p2)

A cylinder inside a cone
sage: u,v = var("u,v")
sage: p1 = parametric_plot3d([cos(u)*v, sin(u)*v, 3/2-3*v/2], (u, 0, 2*pi), (v, 0, 1.5), opacity = 0.5, plot_points=[20,20])
sage: p2 = parametric_plot3d([cos(u)/2, sin(u)/2, v-3/4], (u, 0, 2*pi), (v, 0, 3/2), plot_points=[20,20])
sage: show(p1+p2)

p-adic Seasons Greetings
- I know this is early, but thanks to Robert Bradshaw's p-adic plot function, here is a p-adic Seasons Greetings:

This is the code:
sage: P1 = Zp(3).plot(rgbcolor=(0,1,0))
sage: P2 = Zp(7).plot(rgbcolor=(1,0,0))
sage: P3 = text("$Seasons$ $Greetings$ ",(0.0,1.8))
sage: P4 = text("$from$ $everyone$ $at$ sagemath.org!",(0.1,-1.6))
sage: (P1+P2+P3+P4).show(axes=False)
Lorentz butterfly
"""
Draws Loretz butterfly using matplotlib (2d) or jmol (3d).
Written by Matthew Miller and William Stein.
"""
def butterfly2d():
""""
EXAMPLE:
sage: butterfly2d()
"""
g = Graphics()
x1, y1 = 0, 0
from math import sin, cos, exp, pi
for theta in srange( 0, 10*pi, 0.01 ):
r = exp(cos(theta)) - 2*cos(4*theta) + sin(theta/12)^5
x = r * cos(theta) # Convert polar to rectangular coordinates
y = r * sin(theta)
xx = x*6 + 25 # Scale factors to enlarge and center the curve.
yy = y*6 + 25
if theta != 0:
l = line( [(x1, y1), (xx, yy)], rgbcolor=hue(theta/7 + 4) )
g = g + l
x1, y1 = xx, yy
g.show(dpi=100, axes=False)
def butterfly3d():
""""
EXAMPLE:
sage: butterfly3d()
"""
g = point3d((0,0,0))
x1, y1 = 0, 0
from math import sin, cos, exp, pi
for theta in srange( 0, 10*pi, 0.05):
r = exp(cos(theta)) - 2*cos(4*theta) + sin(theta/12)^5
x = r * cos(theta) # Convert polar to rectangular coordinates
y = r * sin(theta)
xx = x*6 + 25 # Scale factors to enlarge and center the curve.
yy = y*6 + 25
if theta != 0:
l = line3d( [(x1, y1, theta), (xx, yy, theta)],
rgbcolor=hue(theta/7 + 4) )
g = g + l
x1, y1 = xx, yy
g.show(dpi=100, axes=False)


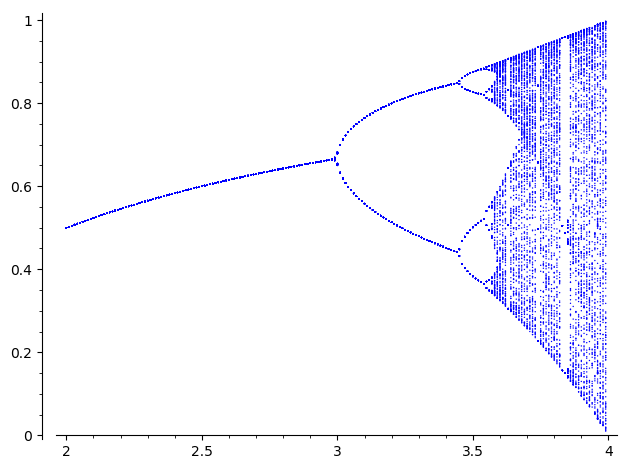
Feigenbaum diagram
Author: Pablo Angulo Posted to sage-devel 2008-09-13. See also https://sage.math.washington.edu:8101/home/pub/3 #Note: Mandelbrot set moved to interact/fractals
#Plots Feigenbaum diagram: divides the parameter interval [2,4] for mu
#into N steps. For each value of the parameter, iterate the discrete
#dynamical system x->mu*x*(1-x), drop the first M1 points in the orbit
#and plot the next M2 points in a (mu,x) diagram
N=200
M1=200
M2=200
x0=0.509434
puntos=[]
for t in range(N):
mu=2.0+2.0*t/N
x=x0
for i in range(M1):
x=mu*x*(1-x)
for i in range(M2):
x=mu*x*(1-x)
puntos.append((mu,x))
point(puntos,pointsize=1)
Sierpinski triangle
- This was a black+white Sierpinski triangle coded by Marshall Hampton, with some slight tweeking by David Joyner to add colors:
def sierpinski_seasons_greetings():
"""
Code by Marshall Hampton.
Colors by David Joyner.
General depth by Rob Beezer.
Copyright Marshall Hampton 2008, licensed
creative commons, attribution share-alike.
"""
depth = 7
nsq = RR(3^(1/2))/2.0
tlist_old = [[[-1/2.0,0.0],[1/2.0,0.0],[0.0,nsq]]]
tlist_new = tlist_old[:]
for ind in range(depth):
for tri in tlist_old:
for p in tri:
new_tri = [[(p[0]+x[0])/2.0, (p[1]+x[1])/2.0] for x in tri]
tlist_new.append(new_tri)
tlist_old = tlist_new[:]
T = tlist_old
N = 4^depth
N1 = N - 3^depth
q1 = sum([line(T[i]+[T[i][0]], rgbcolor = (0,1,0)) for i in range(N1)])
q2 = sum([line(T[i]+[T[i][0]], rgbcolor = (1,0,0)) for i in range(N1,N)])
show(q2+q1, figsize = [6,6*nsq], axes = False)
GIMP was used to add a Season's greetings message:

Also (thanks to Rob Beezer) available in poster form in pdf format: http://sage.math.washington.edu/home/wdj/art/seasons-greetings-sage.pdf, and in A4 size: http://sage.math.washington.edu/home/wdj/art/seasons-greetings-sage-a4.pdf.
Integral Curvature Apollonian Circle Packing
by Marshall Hampton and Carl Witty
def kfun(k1,k2,k3,k4):
"""
The Descartes formula for the curvature of an inverted tangent circle.
"""
return 2*k1+2*k2+2*k3-k4
colorlist = [(1,0,1),(0,1,0),(0,0,1),(1,0,0)]
def circfun(c1,c2,c3,c4):
"""
Computes the inversion of circle 4 in the first three circles.
"""
newk = kfun(c1[3],c2[3],c3[3],c4[3])
newx = (2*c1[0]*c1[3]+2*c2[0]*c2[3]+2*c3[0]*c3[3]-c4[0]*c4[3])/newk
newy = (2*c1[1]*c1[3]+2*c2[1]*c2[3]+2*c3[1]*c3[3]-c4[1]*c4[3])/newk
newcolor = c4[4]
if newk > 0:
newr = 1/newk
elif newk < 0:
newr = -1/newk
else:
newr = Infinity
return [newx, newy, newr, newk, newcolor]
def mcircle(circdata, label = False, thick = 1/10, cutoff = 2000, color = ''):
"""
Draws a circle from the data. label = True
"""
if color == '':
color = colorlist[circdata[4]]
if label==True and circdata[3] > 0 and circdata[2] > 1/cutoff:
lab = text(str(circdata[3]),(circdata[0],circdata[1]), fontsize = \
500*(circdata[2])^(.95), vertical_alignment = 'center', horizontal_alignment \
= 'center', rgbcolor = (0,0,0),zorder=10)
else:
lab = Graphics()
circ = circle((circdata[0],circdata[1]), circdata[2], rgbcolor = (0,0,0), \
thickness = thick)
circ = circ + circle((circdata[0],circdata[1]), circdata[2], rgbcolor = color, \
thickness = thick, fill=True, alpha = .4, zorder=0)
return lab+circ
def add_circs(c1, c2, c3, c4, cutoff = 300):
"""
Find the inversion of c4 through c1,c2,c3. Add the result to circlist,
then (if the result is big enough) recurse.
"""
newcirc = circfun(c1, c2, c3, c4)
if newcirc[3] < cutoff:
circlist.append(newcirc)
add_circs(newcirc, c1, c2, c3, cutoff = cutoff)
add_circs(newcirc, c2, c3, c1, cutoff = cutoff)
add_circs(newcirc, c3, c1, c2, cutoff = cutoff)
zst1 = [0,0,1/2,-2,0]
zst2 = [1/6,0,1/3,3,1]
zst3 = [-1/3,0,1/6,6,2]
zst4 = [-3/14,2/7,1/7,7,3]
circlist = [zst1,zst2,zst3,zst4]
add_circs(zst1,zst2,zst3,zst4,cutoff = 500)
add_circs(zst2,zst3,zst4,zst1,cutoff = 500)
add_circs(zst3,zst4,zst1,zst2,cutoff = 500)
add_circs(zst4,zst1,zst2,zst3,cutoff = 500)
circs = sum([mcircle(q, label = True, thick = 1/2) for q in \
circlist[1:]])
circs = circs + mcircle(circlist[0],color=(1,1,1),thick=1)
circs.save('./Apollonian3.png',axes = False, figsize = [12,12], xmin = \
-1/2, xmax = 1/2, ymin = -1/2, ymax = 1/2)
Call graph of a recursive function
def grafo_llamadas(f):
class G(object):
def __init__(self, f):
self.f=f
self.stack = []
self.g = DiGraph()
def __call__(self, *args):
if self.stack:
sargs = ','.join(str(a) for a in args)
last = ','.join(str(a) for a in self.stack[-1])
if self.g.has_edge(last, sargs):
l = self.g.edge_label(last, sargs)
self.g.set_edge_label(last, sargs, l + 1)
else:
self.g.add_edge(last, sargs, 1)
else:
self.g = DiGraph()
self.stack.append(args)
v = self.f(*args)
self.stack.pop()
return v
def grafo(self):
return self.g
return G(f)
@grafo_llamadas
def particiones(n, k):
if k == n:
return [[1]*n]
if k == 1:
return [[n]]
if not(0 < k < n):
return []
ls1 = [p+[1] for p in particiones(n-1, k-1)]
ls2 = [[parte+1 for parte in p] for p in particiones(n-k, k)]
return ls1 + ls2
particiones(13,5)
g = particiones.grafo()
g.show(edge_labels=True, figsize=(6,6), vertex_size=500, color_by_label=True).
#D3js interactive version (just a screenshot here)
edge_partition = [
[edge for edge in g.edges() if edge[-1]==el]
for el in set(g.edge_labels())
]
g.show(method='js',
edge_labels=True,
vertex_labels=True,
link_distance=90,
charge=-400,
link_strength=2,
force_spring_layout=True,
edge_partition=edge_partition)