|
Size: 91
Comment:
|
Size: 7669
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| Sage-related art [http://modular.math.washington.edu/sage/days2/sage-car.png:Sage car] |
see the attachments This page contains animations drawn using [[http://www.sagemath.org|Sage]]. One can create an animation (.gif) in Sage from a list of graphics objects using the {{{animate}}} command. Currently, to export an animation in .gif format, you might need to install the [[http://www.imagemagick.org|ImageMagick]] command line tools package (the ``convert`` command). See the documentation for more information: {{{ sage: animate? }}} <<TableOfContents>> === The witch of Maria Agnesi === {{attachment:witch.gif}} by Marshall Hampton {{{#!python numbers=none xtreme = 4.1 myaxes = line([[-xtreme,0],[xtreme,0]],rgbcolor = (0,0,0)) myaxes = myaxes + line([[0,-1],[0,2.1]],rgbcolor = (0,0,0)) a = 1.0 t = var('t') npi = RDF(pi) def agnesi(theta): mac = circle((0,a),a,rgbcolor = (0,0,0)) maL = line([[-xtreme,2*a],[xtreme,2*a]]) maL2 = line([[0,0],[2*a*cot(theta),2*a]]) p1 = [2*a*cot(theta),2*a*sin(theta)^2] p2 = [2*a*cot(theta)-cot(theta)*(2*a-2*a*sin(theta)^2),2*a*sin(theta)^2] maL3 = line([p2,p1,[2*a*cot(theta),2*a]], rgbcolor = (1,0,0)) map1 = point(p1) map2 = point(p2) am = line([[-.05,a],[.05,a]], rgbcolor = (0,0,0)) at = text('a',[-.1,a], rgbcolor = (0,0,0)) yt = text('y',[0,2.2], rgbcolor = (0,0,0)) xt = text('x',[xtreme + .1,-.1], rgbcolor = (0,0,0)) matext = at+yt+xt ma = mac+myaxes+maL+am+matext+maL2+map1+maL3+map2 return ma def witchy(theta): ma = agnesi(theta) agplot = parametric_plot([2*a*cot(t),2*a*sin(t)^2],[t,.001,theta], rgbcolor = (1,0,1)) return ma+agplot a2 = animate([witchy(i) for i in srange(.1,npi-.1,npi/60)]+[witchy(i) for i in srange(npi-.1,.1,-npi/60)], xmin = -3, xmax = 3, ymin = 0, ymax = 2.3, figsize = [6,2.3], axes = False) a2.show() }}} === A simpler hypotrochoid === The following animates a hypotrochoid {{{#!python numbers=off import operator # The colors for various elements of the plot: class color: stylus = (1, 0, 0) outer = (.8, .8, .8) inner = (0, 0, 1) plot = (0, 0, 0) center = (0, 0, 0) tip = (1, 0, 0) # and the corresponding line weights: class weight: stylus = 1 outer = 1 inner = 1 plot = 1 center = 5 tip = 5 scale = 1 # The scale of the image animation_delay = .1 # The delay between frames, in seconds # Starting and ending t values t_i = 0 t_f = 2*pi # The t values of the animation frames tvals = srange(t_i, t_f, (t_f-t_i)/60) r_o = 8 # Outer circle radius r_i = 2 # Inner circle radius r_s = 3 # Stylus radius # Coordinates of the center of the inner circle x_c = lambda t: (r_o - r_i)*cos(t) y_c = lambda t: (r_o - r_i)*sin(t) # Parametric coordinates for the plot x = lambda t: x_c(t) + r_s*cos(t*(r_o/r_i)) y = lambda t: y_c(t) - r_s*sin(t*(r_o/r_i)) # Maximum x and y values of the plot x_max = r_o - r_i + r_s y_max = find_maximum_on_interval(y, t_i, t_f)[0] # The plots of the individual elements. Order is important; plots # are stacked from bottom to top as they appear. elements = ( # The outer circle lambda t_f: circle((0, 0), r_o, rgbcolor=color.outer, thickness=weight.outer), # The plot itself lambda t_f: parametric_plot((x, y), t_i, t_f, rgbcolor=color.plot, thickness=weight.plot), # The inner circle lambda t_f: circle((x_c(t_f), y_c(t_f)), r_i, rgbcolor=color.inner, thickness=weight.inner), # The inner circle's center lambda t_f: point((x_c(t_f), y_c(t_f)), rgbcolor=color.center,pointsize=weight.center), # The stylus lambda t_f: line([(x_c(t_f), y_c(t_f)), (x(t_f), y(t_f))], rgbcolor=color.stylus, thickness=weight.stylus), # The stylus' tip lambda t_f: point((x_c(t_f), y_c(t_f)), rgbcolor=color.tip, pointsize=weight.tip), ) # Create the plots and animate them. The animate function renders an # animated gif from the frames provided as its first argument. # Though avid python programmers will find the syntax clear, an # explanation is provided for novices. animation = animate([sum(f(t) for f in elements) for t in tvals], xmin=-x_max, xmax=x_max, ymin=-y_max, ymax=y_max, figsize=(x_max*scale, y_max*scale * y_max/x_max)) animation.show(delay=animation_delay) # The previous could be expressed more pedagogically as follows: # # Evaluate each function in the elements array for the provided t # value: # # plots = lambda t: f(t) for f in elements # # Join a group of plots together to form a single plot: # # def join_plots(plots): # result = plots[0] # for plot in plots[1:]: # result += plot # return result # # or # # join_plots = sum # # Create an array of plots, one for each provided t value: # # frames = [join_plots(plots(t)) for t in tvals] # # Finally, animate the frames: # # animation = animate(frames) }}} === The Towers of Hanoi === {{attachment:hanoi.gif}} by Pablo Angulo {{{#!python numbers=off def plot_towers(towers): '''Returns a plot of the towers of Hanoi Uses matrix_plot ''' K=max(max(l) for l in towers if l)+1 M=matrix(ZZ,K,6*K+7) #first tower for t in range(len(towers[0])): j = t k=towers[0][t]-1 for l in range(K+1-k,K+2+k): M[K-1-j,l]=1 #second tower for t in range(len(towers[1])): j = t k=towers[1][t]-1 for l in range(3*K+3-k,3*K+4+k): M[K-1-j,l]=1 #third tower for t in range(len(towers[2])): j = t k=towers[2][t]-1 for l in range(5*K+5-k,5*K+6+k): M[K-1-j,l]=1 return matrix_plot(M, axes=False) def animate_towers(towers,a=0,b=1,c=2,k=-1): '''Move last k discs from column a into column b Assumes that the last k discs of column a are all smaller than the discs in columns b and c ''' if k==0: return if k==-1: k=len(towers[a]) for t in animate_towers(towers,a,c,b,k-1): yield t disc = towers[a].pop() towers[b].append(disc) yield plot_towers(towers) for t in animate_towers(towers,c,b,a,k-1): yield t towers = (range(4,0,-1),[],[]) initial = plot_towers(towers) frame_list=[initial]+list(animate_towers(towers)) animate(frame_list, axes=False).show(delay=80) }}} === Fibonacci Tiles === {{attachment:fibotile.gif}} by Sébastien Labbé {{{#!python numbers=off sage: path_op = dict(rgbcolor='red', thickness=1) sage: fill_op = dict(rgbcolor='blue', alpha=0.3) sage: options = dict(pathoptions=path_op, filloptions=fill_op, endarrow=False, startpoint=False) sage: G = [words.fibonacci_tile(i).plot(**options) for i in range(7)] sage: a = animate(G) sage: a.show(delay=150) }}} === Pencil of conics === by Pablo Angulo {{attachment:pencil.gif}} {{{ puntos = [(0,0),(0,1),(1,3),(2,1)] K = len(puntos) var('x y') coefs = matrix(QQ, K, 6) for j in range(K): x0, y0 = puntos[j] coefs[j,:] = vector([x0^2, y0^2, x0*y0, x0, y0, 1]) K = coefs.right_kernel() v1 = K.basis()[0] v2 = K.basis()[1] graficas = [] for t in srange(0,2*pi,0.3): c1, c2 = sin(t), cos(t) a,b,c,d,e,f = c1*v1 + c2*v2 curva = a*x^2 + b*y^2 + c*x*y + d*x + e*y + f graficas.append( point2d(puntos,color=(1,0,0),pointsize=30) + implicit_plot(curva,(x,-1,4),(y,-1,4)) ) a = animate(graficas) a.show(delay=10) }}} |
see the attachments
This page contains animations drawn using Sage. One can create an animation (.gif) in Sage from a list of graphics objects using the animate command. Currently, to export an animation in .gif format, you might need to install the ImageMagick command line tools package (the convert command). See the documentation for more information:
sage: animate?
Contents
The witch of Maria Agnesi
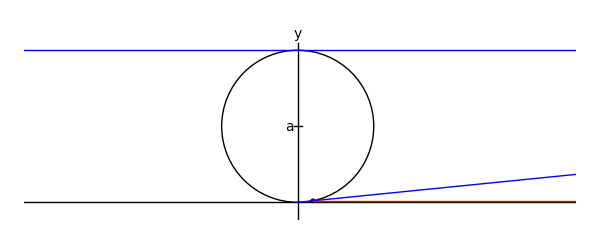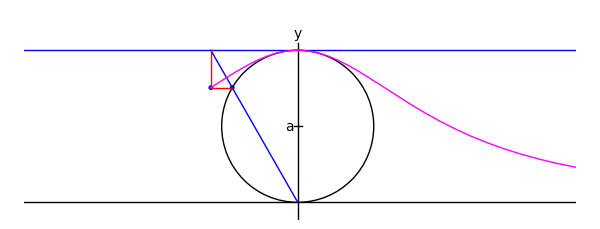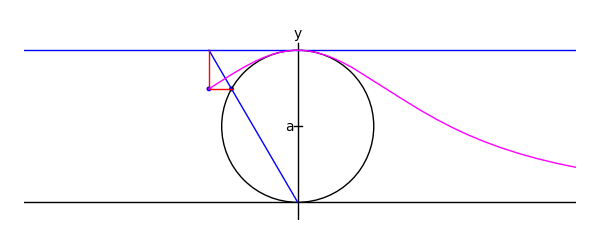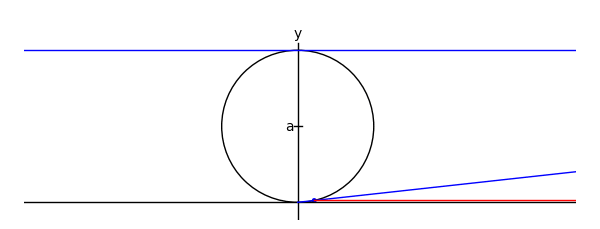
by Marshall Hampton
xtreme = 4.1
myaxes = line([[-xtreme,0],[xtreme,0]],rgbcolor = (0,0,0))
myaxes = myaxes + line([[0,-1],[0,2.1]],rgbcolor = (0,0,0))
a = 1.0
t = var('t')
npi = RDF(pi)
def agnesi(theta):
mac = circle((0,a),a,rgbcolor = (0,0,0))
maL = line([[-xtreme,2*a],[xtreme,2*a]])
maL2 = line([[0,0],[2*a*cot(theta),2*a]])
p1 = [2*a*cot(theta),2*a*sin(theta)^2]
p2 = [2*a*cot(theta)-cot(theta)*(2*a-2*a*sin(theta)^2),2*a*sin(theta)^2]
maL3 = line([p2,p1,[2*a*cot(theta),2*a]], rgbcolor = (1,0,0))
map1 = point(p1)
map2 = point(p2)
am = line([[-.05,a],[.05,a]], rgbcolor = (0,0,0))
at = text('a',[-.1,a], rgbcolor = (0,0,0))
yt = text('y',[0,2.2], rgbcolor = (0,0,0))
xt = text('x',[xtreme + .1,-.1], rgbcolor = (0,0,0))
matext = at+yt+xt
ma = mac+myaxes+maL+am+matext+maL2+map1+maL3+map2
return ma
def witchy(theta):
ma = agnesi(theta)
agplot = parametric_plot([2*a*cot(t),2*a*sin(t)^2],[t,.001,theta], rgbcolor = (1,0,1))
return ma+agplot
a2 = animate([witchy(i) for i in srange(.1,npi-.1,npi/60)]+[witchy(i) for i in srange(npi-.1,.1,-npi/60)], xmin = -3, xmax = 3, ymin = 0, ymax = 2.3, figsize = [6,2.3], axes = False)
a2.show()
A simpler hypotrochoid
The following animates a hypotrochoid
import operator
# The colors for various elements of the plot:
class color:
stylus = (1, 0, 0)
outer = (.8, .8, .8)
inner = (0, 0, 1)
plot = (0, 0, 0)
center = (0, 0, 0)
tip = (1, 0, 0)
# and the corresponding line weights:
class weight:
stylus = 1
outer = 1
inner = 1
plot = 1
center = 5
tip = 5
scale = 1 # The scale of the image
animation_delay = .1 # The delay between frames, in seconds
# Starting and ending t values
t_i = 0
t_f = 2*pi
# The t values of the animation frames
tvals = srange(t_i, t_f, (t_f-t_i)/60)
r_o = 8 # Outer circle radius
r_i = 2 # Inner circle radius
r_s = 3 # Stylus radius
# Coordinates of the center of the inner circle
x_c = lambda t: (r_o - r_i)*cos(t)
y_c = lambda t: (r_o - r_i)*sin(t)
# Parametric coordinates for the plot
x = lambda t: x_c(t) + r_s*cos(t*(r_o/r_i))
y = lambda t: y_c(t) - r_s*sin(t*(r_o/r_i))
# Maximum x and y values of the plot
x_max = r_o - r_i + r_s
y_max = find_maximum_on_interval(y, t_i, t_f)[0]
# The plots of the individual elements. Order is important; plots
# are stacked from bottom to top as they appear.
elements = (
# The outer circle
lambda t_f: circle((0, 0), r_o, rgbcolor=color.outer, thickness=weight.outer),
# The plot itself
lambda t_f: parametric_plot((x, y), t_i, t_f, rgbcolor=color.plot, thickness=weight.plot),
# The inner circle
lambda t_f: circle((x_c(t_f), y_c(t_f)), r_i, rgbcolor=color.inner, thickness=weight.inner),
# The inner circle's center
lambda t_f: point((x_c(t_f), y_c(t_f)), rgbcolor=color.center,pointsize=weight.center),
# The stylus
lambda t_f: line([(x_c(t_f), y_c(t_f)), (x(t_f), y(t_f))], rgbcolor=color.stylus, thickness=weight.stylus),
# The stylus' tip
lambda t_f: point((x_c(t_f), y_c(t_f)), rgbcolor=color.tip, pointsize=weight.tip),
)
# Create the plots and animate them. The animate function renders an
# animated gif from the frames provided as its first argument.
# Though avid python programmers will find the syntax clear, an
# explanation is provided for novices.
animation = animate([sum(f(t) for f in elements)
for t in tvals],
xmin=-x_max, xmax=x_max,
ymin=-y_max, ymax=y_max,
figsize=(x_max*scale, y_max*scale * y_max/x_max))
animation.show(delay=animation_delay)
# The previous could be expressed more pedagogically as follows:
#
# Evaluate each function in the elements array for the provided t
# value:
#
# plots = lambda t: f(t) for f in elements
#
# Join a group of plots together to form a single plot:
#
# def join_plots(plots):
# result = plots[0]
# for plot in plots[1:]:
# result += plot
# return result
#
# or
#
# join_plots = sum
#
# Create an array of plots, one for each provided t value:
#
# frames = [join_plots(plots(t)) for t in tvals]
#
# Finally, animate the frames:
#
# animation = animate(frames)
The Towers of Hanoi

by Pablo Angulo
def plot_towers(towers):
'''Returns a plot of the towers of Hanoi
Uses matrix_plot
'''
K=max(max(l) for l in towers if l)+1
M=matrix(ZZ,K,6*K+7)
#first tower
for t in range(len(towers[0])):
j = t
k=towers[0][t]-1
for l in range(K+1-k,K+2+k):
M[K-1-j,l]=1
#second tower
for t in range(len(towers[1])):
j = t
k=towers[1][t]-1
for l in range(3*K+3-k,3*K+4+k):
M[K-1-j,l]=1
#third tower
for t in range(len(towers[2])):
j = t
k=towers[2][t]-1
for l in range(5*K+5-k,5*K+6+k):
M[K-1-j,l]=1
return matrix_plot(M, axes=False)
def animate_towers(towers,a=0,b=1,c=2,k=-1):
'''Move last k discs from column a into column b
Assumes that the last k discs of column a are all smaller
than the discs in columns b and c
'''
if k==0: return
if k==-1: k=len(towers[a])
for t in animate_towers(towers,a,c,b,k-1):
yield t
disc = towers[a].pop()
towers[b].append(disc)
yield plot_towers(towers)
for t in animate_towers(towers,c,b,a,k-1):
yield t
towers = (range(4,0,-1),[],[])
initial = plot_towers(towers)
frame_list=[initial]+list(animate_towers(towers))
animate(frame_list, axes=False).show(delay=80)
Fibonacci Tiles

by Sébastien Labbé
sage: path_op = dict(rgbcolor='red', thickness=1)
sage: fill_op = dict(rgbcolor='blue', alpha=0.3)
sage: options = dict(pathoptions=path_op, filloptions=fill_op, endarrow=False, startpoint=False)
sage: G = [words.fibonacci_tile(i).plot(**options) for i in range(7)]
sage: a = animate(G)
sage: a.show(delay=150)
Pencil of conics
by Pablo Angulo 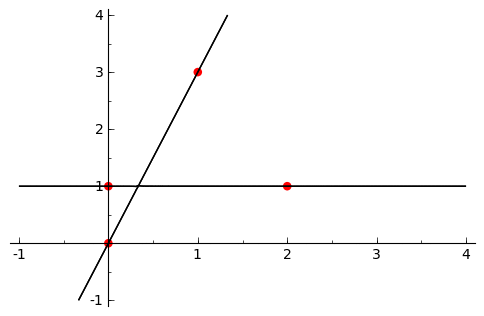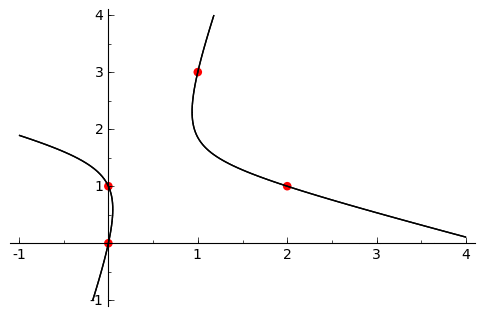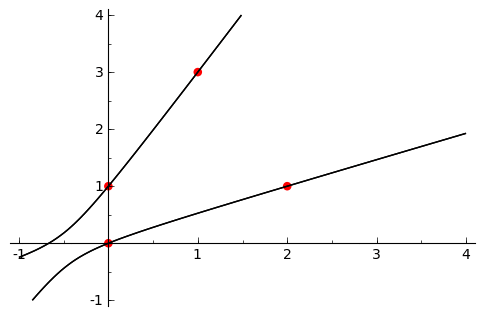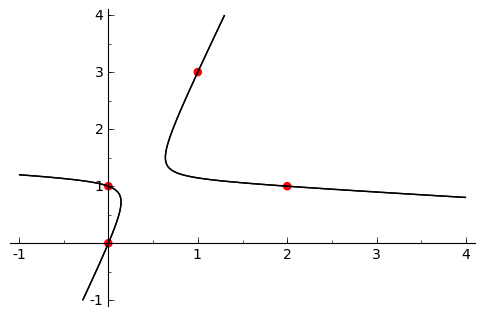
puntos = [(0,0),(0,1),(1,3),(2,1)]
K = len(puntos)
var('x y')
coefs = matrix(QQ, K, 6)
for j in range(K):
x0, y0 = puntos[j]
coefs[j,:] = vector([x0^2, y0^2, x0*y0, x0, y0, 1])
K = coefs.right_kernel()
v1 = K.basis()[0]
v2 = K.basis()[1]
graficas = []
for t in srange(0,2*pi,0.3):
c1, c2 = sin(t), cos(t)
a,b,c,d,e,f = c1*v1 + c2*v2
curva = a*x^2 + b*y^2 + c*x*y + d*x + e*y + f
graficas.append( point2d(puntos,color=(1,0,0),pointsize=30) +
implicit_plot(curva,(x,-1,4),(y,-1,4)) )
a = animate(graficas)
a.show(delay=10)