|
Size: 1350
Comment: Add notes on spkg-configure
|
Size: 21230
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 9: | Line 9: |
| SageMath 9.0 was the first version of Sage running on Python 3 by default. Sage 9.1 continues to support Python 2. See [[Python3-Switch]] for more details |
[[ReleaseTours/sage-9.0|SageMath 9.0]] was the first version of Sage running on Python 3 by default. '''Sage 9.1 continues to support both Python 2 and Python 3.''' In Sage 9.1, we have made [[https://trac.sagemath.org/query?component=python3&milestone=sage-9.1&or&keywords=~py3&milestone=sage-9.1&groupdesc=1&group=status&max=1500&col=id&col=summary&col=component&col=time&col=changetime&col=author&col=reviewer&col=keywords&order=component|some further improvements regarding Python 3 support]]. In particular, !SageMath now supports underscored numbers [[https://www.python.org/dev/peps/pep-0515/|PEP 515]] (py3); the fix was done in [[https://trac.sagemath.org/ticket/28490|Trac #28490]]: {{{ sage: 1_000_000 + 3_000 1003000 }}} The next release, [[ReleaseTours/sage-9.2|SageMath 9.2]], will remove support for Python 2. See [[Python3-Switch]] for more details. |
| Line 15: | Line 22: |
| The SageMath distribution continues to vendor versions of required software packages ("spkgs") that work well together. In order to reduce compilation times and the size of the SageMath installation, |
The !SageMath distribution continues to vendor versions of required software packages ("SPKGs") that work well together. In order to reduce compilation times and the size of the Sage installation, |
| Line 20: | Line 26: |
| has made it possible to use many system packages provided by the OS distribution instead of building SageMath's own copies. This so-called "spkg-configure" mechanism runs at the beginning of a build from source, during the `./configure` phase. Sage 9.1 is adding many packages to this mechanism. == Availability of Sage 9.1 in distributions == |
has made it possible to '''use many system packages provided by the OS distribution''' (or by the Homebrew or conda-forge distributions) instead of building !SageMath's own copies. This so-called "spkg-configure" mechanism runs at the beginning of a build from source, during the `./configure` phase. (See the sage-devel threads [[https://groups.google.com/d/msg/sage-devel/nTwhCV89FXE/_7GdzGy4BgAJ|"Brainstorming about Sage dependencies from system packages"]] (May 2017) and [[https://groups.google.com/d/msg/sage-devel/1at1p25IHnQ/ZHcpRjtQAwAJ|"conditionalise installation of many spkg's?"]] (Nov 2017) for its origins and [[https://trac.sagemath.org/ticket/24919|Trac #24919]] for its initial implementation.) Sage 9.1 is adding many packages to this mechanism, including `openblas`, `gsl`, `r`, `boost`, `libatomic`, `cddlib`, `tachyon`, `nauty`, `sqlite`, `planarity`, `fplll`, `brial`, `flintqs`, `ppl`, `libbraiding`, `cbc`, `gfan`, and `python3`. As to the latter, '''!SageMath will now make use of a suitable installation of Python 3.7.x in your system by setting up a [[https://docs.python.org/3/library/venv.html|venv]]''' (Python 3 virtual environment). New in Sage 9.1 is also a '''database of system packages''' equivalent to our SPKGs. At the end of a `./configure` run, you will see messages like the following: {{{ configure: notice: the following SPKGs did not find equivalent system packages: arb boost boost_cropped bzip2 ... yasm zeromq zlib checking for the package system in use... debian configure: hint: installing the following system packages is recommended and may avoid building some of the above SPKGs from source: configure: $ sudo apt-get install libflint-arb-dev ... yasm libzmq3-dev libz-dev configure: After installation, re-run configure using: configure: $ ./config.status --recheck && ./config.status }}} We also use the same database to update our installation manual automatically. === Status of Cygwin support === Thanks to the [[https://trac.sagemath.org/query?component=porting%3A+Cygwin&groupdesc=1&group=milestone&max=1500&col=id&col=summary&col=author&col=reviewer&col=time&col=changetime&col=keywords&order=component|hard work of our Cygwin maintainers]], in particular during the 8.x release cycles, building Sage on Windows using Cygwin64 is fully supported. Sage 9.1 reflects this by integrating the instructions for building from source on Cygwin into its documentation. === For developers === For developers who wish to help improve the portability of !SageMath, there is a new power tool: A '''tox configuration''' that automatically builds and tests Sage within Docker containers running various Linux distributions (`ubuntu-trusty` through `-focal`, `debian-jessie` through `-sid`, `linuxmint-17` through `-19.3`, `fedora-26` through `-32`, `centos-7` and `-8`, `archlinux`, `slackware-14.2`), each in several configurations regarding what system packages are installed. Thus, it is no longer necessary for developers to have access to a machine running `fedora-29`, say, to verify whether the Sage distribution works there; instead, you just type: {{{ tox -e docker-fedora-29-standard -- build ptest }}} The `Dockerfile`s are generated automatically on the fly using the same database of system packages that provides information to users. See the [[https://git.sagemath.org/sage.git/diff?id2=6a4580546f25fa62f38b3490e2d0120975371379&id=99aca39dea0226372a3f12aed3a13301a3380ff4|new section on "portability testing" in the Developer's Guide]] for details. An entry point for developers who wish to improve the testing infrastructure is the [[https://trac.sagemath.org/ticket/29060|Meta-Ticket #29060: Add Dockerfiles and CI scripts for integration testing]]. See also the broader [[https://trac.sagemath.org/ticket/29133|Meta-Meta-Ticket #29133]]. === For packagers === Although we now have continuous integration environments for testing the interaction of the Sage distribution with most major Linux distributions, we are still missing a few. Adding them will enable all Sage developers to check that their changes do not break things on your distribution. == Package updates == We have only made minor updates to standard packages: * dateutil – 2.8.1 (from 2.5.3) * fplll – 5.3.2 (from 5.2.1) * fpylll – 0.5.1.dev (from 0.4.1dev) * freetype – 2.10.1 * m4ri – 20200115 * m4rie – 20200115 * matplotlib – 2.2.5 (from 2.2.4) * ntl – 11.4.3 (from 11.3.2) * numpy – 1.16.6 (from 1.16.1) * openblas – 0.3.9 * pkgconfig – 1.5.1 (from 1.4.0) * pyzmq – 19.0.0 (from 18.1) * sage_brial – 1.2.5 (this is the python module of the brial package) * scipy – 1.2.3 (from 1.2.0) * sympy – 1.5 (from 1.4) * traitlets – 4.3.3 We expect to make larger package updates in the 9.2 release. === For developers === Preparing and testing package updates has become easier. The new optional field `upstream_url` in `checksums.ini` holds an URL to the upstream package archive, see for example [[https://git.sagemath.org/sage.git/tree/build/pkgs/numpy/checksums.ini?h=develop|build/pkgs/numpy/checksums.ini]]. Note that, like the `tarball` field, the `upstream_url` is a template; the word `VERSION` is substituted with the actual version. The package can be updated by simply typing `./sage -package -update numpy 3.14.59`; this will automatically download the archive and update the `build/pkgs/` information. Developers who wish to test a package update from a Trac branch before the archive is available on a Sage mirror can do so by configuring their Sage tree using `./configure --enable-download-from-upstream-url`. Every Sage developer now has easy access to "their own" set of 40 two-core virtual machines running Linux, macOS, and Windows through !GitHub Actions. To automatically test a branch on a multitude of our supported platforms, it suffices to create a fork of the [[https://github.com/sagemath/sage|sagemath/sage]] repository on !GitHub, enable !GitHub Actions, add the repository as a remote, create a tag and push the tag to the remote. After ... a ... while, your test results will be available — like the ones at [[https://github.com/sagemath/sage/actions|sagemath/sage Actions]]. We hope that this new testing infrastructure will reduce the FUD in the process of upgrading packages. == Polyhedral geometry == There is now a catalog for common polyhedral cones, e.g. {{{ sage: cones.nonnegative_orthant(5) 5-d cone in 5-d lattice N }}} New features for polyhedra: {{{ sage: P = polytopes.cube(intervals='zero_one') # obtain others than the standard cube sage: P = matrix([[0,1,0],[0,1,1],[1,0,0]])*P # linear transformations sage: it = P.face_generator() # a (fast and efficient) face generator sage: next(it) A 3-dimensional face of a Polyhedron in ZZ^3 defined as the convex hull of 8 vertices sage: next(it) A -1-dimensional face of a Polyhedron in ZZ^3 sage: f = next(it) sage: f.normal_cone() # normal cone for faces A 1-dimensional polyhedron in ZZ^3 defined as the convex hull of 1 vertex and 1 ray sage: P.an_affine_basis() # an_affine_basis and a_maximal_chain [A vertex at (0, 0, 0), A vertex at (1, 1, 0), A vertex at (0, 0, 1), A vertex at (0, 1, 0)] sage: P = polytopes.hypercube(4) sage: P.flag_f_vector(0,3) # flag_f_vector is exposed 64 }}} Regarding the optional package `normaliz` there are some news as well: {{{ sage: P = polytopes.cube(intervals=[[0,1],[0,2],[0,3]], backend='normaliz') sage: save(P, '/tmp/this_takes_very_long_so_we_save_it') # saving works now sage: sage: P.h_star_vector() # compute the h_star_vector with normaliz [1, 20, 15] }}} There are also some bug fixes and other improvements. For more details see the [[https://trac.sagemath.org/wiki/SagePolyhedralGeometry#release_9.1|release notes for optimization and polyhedral geometry softwares interactions in Sage]]. == Improvements in the three.js 3D viewer == [[https://doc.sagemath.org/html/en/reference/plot3d/threejs.html|Three.js]] has become the default 3D viewer in SageMath 9.0. In this release, some improvements have been performed: * '''bug fixes:''' plot of vectors (Trac ticket [[https://trac.sagemath.org/ticket/29206|#29206]]), plot of a single text ([[https://trac.sagemath.org/ticket/29227|#29227]]), method ''plot3d'' transforming a 2D object into a 3D one ([[https://trac.sagemath.org/ticket/29251|#29251]]) * '''code cleanup''' to prepare for camera viewpoint option ([[https://trac.sagemath.org/ticket/29250|#29250]]) == Integral curves over finite fields == A dream has come true! The integral curves over finite fields are now attached with the global function field machinery of Sage. This is a short tour: {{{ sage: A.<x,y> = AffineSpace(GF(16),2) sage: C = Curve(y^3 + x^3*y + x); C # Klein quartic Affine Plane Curve over Finite Field in z4 of size 2^4 defined by x^3*y + y^3 + x sage: C.function_field() Function field in y defined by y^3 + x^3*y + x sage: C.genus() 3 sage: C.closed_points() [Point (x, y), Point (x + (z4), y + (z4^3 + z4^2)), Point (x + (z4^2), y + (z4^3 + z4^2 + z4 + 1)), Point (x + (z4^3), y + (z4^2 + z4)), Point (x + (z4 + 1), y + (z4^3 + z4)), Point (x + (z4^2 + z4), y + (z4^2 + z4 + 1)), Point (x + (z4^2 + z4), y + (z4^3 + 1)), Point (x + (z4^2 + z4), y + (z4^3 + z4^2 + z4)), Point (x + (z4^3 + z4^2), y + (z4^2 + z4 + 1)), Point (x + (z4^2 + 1), y + (z4^3)), Point (x + (z4^3 + z4), y + (z4^2 + z4 + 1)), Point (x + (z4^2 + z4 + 1), y + (z4^2 + z4)), Point (x + (z4^2 + z4 + 1), y + (z4^3 + z4 + 1)), Point (x + (z4^2 + z4 + 1), y + (z4^3 + z4^2 + 1)), Point (x + (z4^3 + z4^2 + z4 + 1), y + (z4^2 + z4))] sage: p1, p2 = _[:2] sage: P1 = p1.place() sage: P2 = p2.place() sage: D = 5 * P1 - P2 sage: D.basis_function_space() # Riemann-Roch space [(x + z4)/x, 1/x^2*y + (z4^2 + z4)/x] sage: D.dimension() 2 sage: f1, f2 = D.basis_function_space() [(x + z4)/x, 1/x^2*y + (z4^2 + z4)/x] sage: f1.zeros() [Place (x + z4, y^2 + (z4^3 + z4^2)*y + z4^2 + z4 + 1), Place (x + z4, y + z4^3 + z4^2)] sage: Q1, Q2 = _ sage: q1 = C.place_to_closed_point(Q1); q1 Point (y^2 + (z4^3 + z4^2)*y + (z4^2 + z4 + 1), x + (z4)) sage: q1.degree() 2 sage: q1 = C.place_to_closed_point(Q1); q1 Point (y^2 + (z4^3 + z4^2)*y + (z4^2 + z4 + 1), x + (z4)) sage: q1.degree() 2 sage: q2 = C.place_to_closed_point(Q2) sage: q2.degree() 1 sage: q2.rational_point() (z4, z4^3 + z4^2) sage: _ in C True }}} == Puiseux series == After 11 years [[https://trac.sagemath.org/ticket/4618|Trac #4618]] has come to an end. Thus, Puiseux series are available, right now: {{{ sage: R.<x> = PuiseuxSeriesRing(QQ) sage: p = x^(-7/2) + 3 + 5*x^(1/2) - 7*x^3 sage: 1/p x^(7/2) - 3*x^7 - 5*x^(15/2) + 7*x^10 + 9*x^(21/2) + 30*x^11 + 25*x^(23/2) + O(x^(27/2)) }}} == Localization == Integral domains can be localized at finite sets of their non invertible elements: {{{ sage: L = ZZ.localization(45); L Integer Ring localized at (3, 5) sage: [1/l in L for l in range(1,6)] [True, False, True, False, True] sage: P.<x,y,z> = QQ[] sage: d = x^2+y^2+z^2 sage: Ld = P.localization(d); Ld Multivariate Polynomial Ring in x, y, z over Rational Field localized at (x^2 + y^2 + z^2,) sage: (x + y + z)/d in Ld True }}} == Ariki–Koike algebras == An Ariki–Koike algebra (aka cyclotomic Hecke algebra) is a generalization of the Iwahori–Hecke algebra to the complex reflection group G(r,1,n) instead of a Coxeter group. == Graph theory == === Arboricity === The [[https://en.wikipedia.org/wiki/Arboricity|arboricity]] of a graph can now be computed using the {{{arboricity}}} function ([[https://trac.sagemath.org/ticket/19053|#19053]]). === MCS traversal and clique separators === Ticket [[https://trac.sagemath.org/ticket/28473|#28473]] introduced the following methods to the {{{Graph}}} class: * {{{maximum_cardinality_search}}} for the [[https://doi.org/10.1137/0213035|Maximal Cardinality Search (MCS)]] graph traversal (in {{{O(n+m)}}} time), * {{{maximum_cardinality_search_M}}}, an extension of MCS that also returns a minimal triangulation (in {{{O(n.m)}}} time), and * {{{atoms_and_clique_separators}}}, a method that decomposes the graph according clique minimal separators and returns the atoms and the clique minimal separators (in {{{O(n.m)}}} time). === Hypergraphs === Checking whether a uniform hypergraph has a [[https://en.wikipedia.org/wiki/Hypergraph#Acyclicity|Berge-cycle]] can be done using the {{{is_berge_cyclic}}} method of ticket [[https://trac.sagemath.org/ticket/21931|#21931]]. === Generator for cube-connected cycles === There is now a generator for [[https://en.wikipedia.org/wiki/Cube-connected_cycles|cube-connected cycles]] ([[https://trac.sagemath.org/ticket/21423|#21423]]): {{{ sage: g = graphs.CubeConnectedCycle(3) Cube-Connected Cycle of dimension 3: Graph on 24 vertices }}} {{attachment:cube-connected-cycles.png|The cube-connected-cycles graph of dim 3}} === Enumeration of minimal dominating sets === The {{{minimal_dominating_sets}}} method of a {{{Graph}}} is a generator of its minimal dominating sets ([[https://trac.sagemath.org/ticket/27424|#27424]]): {{{ #!python sage: g = graphs.PathGraph(5) sage: list(g.minimal_dominating_sets()) [{0, 2, 4}, {1, 4}, {0, 3}, {1, 3}] }}} == Manifolds == === Degenerate manifolds and submanifolds === Manifolds equipped with a degenerate metric have been introduced in this release. See the [[https://doc.sagemath.org/html/en/reference/manifolds/sage/manifolds/differentiable/degenerate_submanifold.html|documentation]] and well as these Jupyter notebooks: [[https://nbviewer.jupyter.org/github/sagemanifolds/SageManifolds/blob/master/Notebooks/SM_degenerate_metric.ipynb|example 1]] and [[https://nbviewer.jupyter.org/github/sagemanifolds/SageManifolds/blob/master/Notebooks/SM_Schwarzschild_horizon_degen.ipynb|example 2]] === More functionatilities in index notation for tensors === [[https://doc.sagemath.org/html/en/reference/tensor_free_modules/sage/tensor/modules/tensor_with_indices.html|Index notation]] to indicate operations like contractions has been enhanced. For instance, a sum can be introduced in a contraction: {{{ #!python sage: E.<x,y> = EuclideanSpace() sage: v = E.vector_field(-y, x) sage: t = E.tensor_field(0, 2, [[1, x], [-2*y, x^2]]) sage: v['j']*(t['_ij'] + t['_ji']) == v.contract(2*t.symmetrize()) True }}} === Applying a function to all components of a tensor field === The new method [[https://doc.sagemath.org/html/en/reference/manifolds/sage/manifolds/differentiable/tensorfield.html#sage.manifolds.differentiable.tensorfield.TensorField.apply_map|apply_map()]] of tensor fields allows one to perform operations like factorization, expansion, simplification or substitution on all components of a tensor field: {{{ #!python sage: M = Manifold(2, 'M') sage: X.<x,y> = M.chart() sage: v = M.vector_field(x^2 - y^2, x*(y^2 - y), name='v') sage: v.display() v = (x^2 - y^2) d/dx + (y^2 - y)*x d/dy sage: v.apply_map(factor) sage: v.display() v = (x + y)*(x - y) d/dx + x*(y - 1)*y d/dy }}} === Other changes === Some improvements and bug fixes have been introduced in this release. See the [[https://sagemanifolds.obspm.fr/changelog.html|full change log]]. == Configuration changes == === Easier installation of optional linear and mixed integer linear optimization backends === It is no longer necessary to recompile sagelib if you wish to use one of the state-of-the-art LP/MIP solvers COIN-OR CBC, CPLEX, or Gurobi, instead of the default (GLPK). The simplified new installation procedure is explained in the [[https://git.sagemath.org/sage.git/tree/src/doc/en/thematic_tutorials/linear_programming.rst?id=5fa32aa9f8acede36a665baf6b474af886c95956#n438|Thematic Tutorial on Linear Programming]]. (If you cannot update to 9.1 just yet, you can retroactively get the same feature in your installation of Sage too by pip-installing one of the packages [[https://github.com/mkoeppe/sage-numerical-backends-cplex|sage-numerical-backends-cplex]], [[https://github.com/mkoeppe/sage-numerical-backends-coin|sage-numerical-backends-coin]], [[https://github.com/mkoeppe/sage-numerical-backends-gurobi|sage-numerical-backends-gurobi]].) === New way to install optional and experimental packages === It is now possible to use `./configure` options to request the installation of optional and experimental packages at the next run of `make`. For example, type {{{ $ ./configure --enable-4ti2 --enable-lrslib }}} to request these two packages to be installed. Check `./configure --help` for a list of all options. (The traditional way of installing optional packages, `sage -i`, still works.) Likewise, optional and experimental packages can be requested to be uninstalled at the next run of `make` by using `--disable-SPKG` options. === For developers and packagers === Happy news! The configuration file * `src/bin/sage-env-config` (installed as `$SAGE_LOCAL/bin/sage-env-config`) (introduced 4 years ago in [[https://trac.sagemath.org/ticket/21479|Trac #21479]]) finally has some company. Two new configuration files, also generated by the Sage distribution's `./configure` script, are taking over some of its duties. * `build/bin/sage-build-env-config` (not installed) provides configuration variables that are used only while building packages. * `build/pkgs/sage_conf/src/sage_conf.py` (installed as Python module `sage_conf`) provides configuration variables that are needed by the Sage library runtime, but are not needed in the form of environment variables. (They are available to the Sage library even when it is imported into a Python running outside of the environment set up by `sage-env`.) See [[https://trac.sagemath.org/ticket/21707|Meta-ticket #21707: Split sage-env into 5 to clean up sage configuration]] for details and planned future work. == Spring cleaning == * [[https://trac.sagemath.org/ticket/29636|Trac #29636: Delete changelog sections from all SPKG information files]]; they were deprecated in favor of using Trac years ago. The contributions of Sage developers maintaining SPKGs are documented by our [[http://www.sagemath.org/changelogs/index.html|historical changelogs]]. * [[https://trac.sagemath.org/ticket/29406|Trac #29406: Remove documentation on creating old-style SPKGs]], [[https://trac.sagemath.org/ticket/29383|Trac #29383: Remove related scripts]] * [[https://trac.sagemath.org/query?milestone=sage-9.1&summary=~clean&or&component=refactoring&milestone=sage-9.1&or&component=scripts&milestone=sage-9.1&groupdesc=1&group=status&max=1500&col=id&col=summary&col=component&col=time&col=changetime&col=author&col=reviewer&col=keywords&order=component|Remove numerous deprecated items, fix coding style, refactoring]] == Availability of Sage 9.1 and installation help == Sage 9.1 has not been released yet. See [[https://groups.google.com/forum/#!forum/sage-release|sage-release]] for announcements of beta versions and release candidates. === Availability in distributions === |
| Line 32: | Line 361: |
| === Installation FAQ === See [[https://groups.google.com/forum/#!forum/sage-release|sage-release]], [[https://groups.google.com/forum/#!forum/sage-devel|sage-devel]]. |
|
| Line 34: | Line 367: |
| - Release announcements: See https://groups.google.com/forum/#!forum/sage-release - [[https://trac.sagemath.org/query?milestone=sage-9.1&groupdesc=1&group=status&max=1500&col=id&col=summary&col=author&col=reviewer&col=time&col=changetime&col=component&col=keywords&order=component|Trac tickets with milestone 9.1]] |
* [[https://trac.sagemath.org/query?milestone=sage-9.1&groupdesc=1&group=status&max=1500&col=id&col=summary&col=author&col=reviewer&col=time&col=changetime&col=component&col=keywords&order=component|Trac tickets with milestone 9.1]] |
Sage 9.1 Release Tour
in progress (2020)
Contents
-
Sage 9.1 Release Tour
- Python 3 transition
- Portability improvements, increased use of system packages
- Package updates
- Polyhedral geometry
- Improvements in the three.js 3D viewer
- Integral curves over finite fields
- Puiseux series
- Localization
- Ariki–Koike algebras
- Graph theory
- Manifolds
- Configuration changes
- Spring cleaning
- Availability of Sage 9.1 and installation help
- More details
Python 3 transition
SageMath 9.0 was the first version of Sage running on Python 3 by default. Sage 9.1 continues to support both Python 2 and Python 3.
In Sage 9.1, we have made some further improvements regarding Python 3 support. In particular, SageMath now supports underscored numbers PEP 515 (py3); the fix was done in Trac #28490:
sage: 1_000_000 + 3_000 1003000
The next release, SageMath 9.2, will remove support for Python 2. See Python3-Switch for more details.
Portability improvements, increased use of system packages
The SageMath distribution continues to vendor versions of required software packages ("SPKGs") that work well together.
In order to reduce compilation times and the size of the Sage installation, a development effort ongoing since the 8.x release series has made it possible to use many system packages provided by the OS distribution (or by the Homebrew or conda-forge distributions) instead of building SageMath's own copies.
This so-called "spkg-configure" mechanism runs at the beginning of a build from source, during the ./configure phase.
(See the sage-devel threads "Brainstorming about Sage dependencies from system packages" (May 2017) and "conditionalise installation of many spkg's?" (Nov 2017) for its origins and Trac #24919 for its initial implementation.)
Sage 9.1 is adding many packages to this mechanism, including openblas, gsl, r, boost, libatomic, cddlib, tachyon, nauty, sqlite, planarity, fplll, brial, flintqs, ppl, libbraiding, cbc, gfan, and python3. As to the latter, SageMath will now make use of a suitable installation of Python 3.7.x in your system by setting up a venv (Python 3 virtual environment).
New in Sage 9.1 is also a database of system packages equivalent to our SPKGs. At the end of a ./configure run, you will see messages like the following:
configure: notice: the following SPKGs did not find equivalent system packages: arb boost boost_cropped bzip2 ... yasm zeromq zlib checking for the package system in use... debian configure: hint: installing the following system packages is recommended and may avoid building some of the above SPKGs from source: configure: $ sudo apt-get install libflint-arb-dev ... yasm libzmq3-dev libz-dev configure: After installation, re-run configure using: configure: $ ./config.status --recheck && ./config.status
We also use the same database to update our installation manual automatically.
Status of Cygwin support
Thanks to the hard work of our Cygwin maintainers, in particular during the 8.x release cycles, building Sage on Windows using Cygwin64 is fully supported. Sage 9.1 reflects this by integrating the instructions for building from source on Cygwin into its documentation.
For developers
For developers who wish to help improve the portability of SageMath, there is a new power tool: A tox configuration that automatically builds and tests Sage within Docker containers running various Linux distributions (ubuntu-trusty through -focal, debian-jessie through -sid, linuxmint-17 through -19.3, fedora-26 through -32, centos-7 and -8, archlinux, slackware-14.2), each in several configurations regarding what system packages are installed. Thus, it is no longer necessary for developers to have access to a machine running fedora-29, say, to verify whether the Sage distribution works there; instead, you just type:
tox -e docker-fedora-29-standard -- build ptest
The Dockerfiles are generated automatically on the fly using the same database of system packages that provides information to users. See the new section on "portability testing" in the Developer's Guide for details.
An entry point for developers who wish to improve the testing infrastructure is the Meta-Ticket #29060: Add Dockerfiles and CI scripts for integration testing. See also the broader Meta-Meta-Ticket #29133.
For packagers
Although we now have continuous integration environments for testing the interaction of the Sage distribution with most major Linux distributions, we are still missing a few. Adding them will enable all Sage developers to check that their changes do not break things on your distribution.
Package updates
We have only made minor updates to standard packages:
- dateutil – 2.8.1 (from 2.5.3)
- fplll – 5.3.2 (from 5.2.1)
- fpylll – 0.5.1.dev (from 0.4.1dev)
- freetype – 2.10.1
- m4ri – 20200115
- m4rie – 20200115
- matplotlib – 2.2.5 (from 2.2.4)
- ntl – 11.4.3 (from 11.3.2)
- numpy – 1.16.6 (from 1.16.1)
- openblas – 0.3.9
- pkgconfig – 1.5.1 (from 1.4.0)
- pyzmq – 19.0.0 (from 18.1)
- sage_brial – 1.2.5 (this is the python module of the brial package)
- scipy – 1.2.3 (from 1.2.0)
- sympy – 1.5 (from 1.4)
- traitlets – 4.3.3
We expect to make larger package updates in the 9.2 release.
For developers
Preparing and testing package updates has become easier. The new optional field upstream_url in checksums.ini holds an URL to the upstream package archive, see for example build/pkgs/numpy/checksums.ini. Note that, like the tarball field, the upstream_url is a template; the word VERSION is substituted with the actual version. The package can be updated by simply typing ./sage -package -update numpy 3.14.59; this will automatically download the archive and update the build/pkgs/ information.
Developers who wish to test a package update from a Trac branch before the archive is available on a Sage mirror can do so by configuring their Sage tree using ./configure --enable-download-from-upstream-url.
Every Sage developer now has easy access to "their own" set of 40 two-core virtual machines running Linux, macOS, and Windows through GitHub Actions. To automatically test a branch on a multitude of our supported platforms, it suffices to create a fork of the sagemath/sage repository on GitHub, enable GitHub Actions, add the repository as a remote, create a tag and push the tag to the remote. After ... a ... while, your test results will be available — like the ones at sagemath/sage Actions. We hope that this new testing infrastructure will reduce the FUD in the process of upgrading packages.
Polyhedral geometry
There is now a catalog for common polyhedral cones, e.g.
sage: cones.nonnegative_orthant(5) 5-d cone in 5-d lattice N
New features for polyhedra:
sage: P = polytopes.cube(intervals='zero_one') # obtain others than the standard cube sage: P = matrix([[0,1,0],[0,1,1],[1,0,0]])*P # linear transformations sage: it = P.face_generator() # a (fast and efficient) face generator sage: next(it) A 3-dimensional face of a Polyhedron in ZZ^3 defined as the convex hull of 8 vertices sage: next(it) A -1-dimensional face of a Polyhedron in ZZ^3 sage: f = next(it) sage: f.normal_cone() # normal cone for faces A 1-dimensional polyhedron in ZZ^3 defined as the convex hull of 1 vertex and 1 ray sage: P.an_affine_basis() # an_affine_basis and a_maximal_chain [A vertex at (0, 0, 0), A vertex at (1, 1, 0), A vertex at (0, 0, 1), A vertex at (0, 1, 0)] sage: P = polytopes.hypercube(4) sage: P.flag_f_vector(0,3) # flag_f_vector is exposed 64
Regarding the optional package normaliz there are some news as well:
sage: P = polytopes.cube(intervals=[[0,1],[0,2],[0,3]], backend='normaliz') sage: save(P, '/tmp/this_takes_very_long_so_we_save_it') # saving works now sage: sage: P.h_star_vector() # compute the h_star_vector with normaliz [1, 20, 15]
There are also some bug fixes and other improvements. For more details see the release notes for optimization and polyhedral geometry softwares interactions in Sage.
Improvements in the three.js 3D viewer
Three.js has become the default 3D viewer in SageMath 9.0. In this release, some improvements have been performed:
bug fixes: plot of vectors (Trac ticket #29206), plot of a single text (#29227), method plot3d transforming a 2D object into a 3D one (#29251)
code cleanup to prepare for camera viewpoint option (#29250)
Integral curves over finite fields
A dream has come true! The integral curves over finite fields are now attached with the global function field machinery of Sage. This is a short tour:
sage: A.<x,y> = AffineSpace(GF(16),2) sage: C = Curve(y^3 + x^3*y + x); C # Klein quartic Affine Plane Curve over Finite Field in z4 of size 2^4 defined by x^3*y + y^3 + x sage: C.function_field() Function field in y defined by y^3 + x^3*y + x sage: C.genus() 3 sage: C.closed_points() [Point (x, y), Point (x + (z4), y + (z4^3 + z4^2)), Point (x + (z4^2), y + (z4^3 + z4^2 + z4 + 1)), Point (x + (z4^3), y + (z4^2 + z4)), Point (x + (z4 + 1), y + (z4^3 + z4)), Point (x + (z4^2 + z4), y + (z4^2 + z4 + 1)), Point (x + (z4^2 + z4), y + (z4^3 + 1)), Point (x + (z4^2 + z4), y + (z4^3 + z4^2 + z4)), Point (x + (z4^3 + z4^2), y + (z4^2 + z4 + 1)), Point (x + (z4^2 + 1), y + (z4^3)), Point (x + (z4^3 + z4), y + (z4^2 + z4 + 1)), Point (x + (z4^2 + z4 + 1), y + (z4^2 + z4)), Point (x + (z4^2 + z4 + 1), y + (z4^3 + z4 + 1)), Point (x + (z4^2 + z4 + 1), y + (z4^3 + z4^2 + 1)), Point (x + (z4^3 + z4^2 + z4 + 1), y + (z4^2 + z4))] sage: p1, p2 = _[:2] sage: P1 = p1.place() sage: P2 = p2.place() sage: D = 5 * P1 - P2 sage: D.basis_function_space() # Riemann-Roch space [(x + z4)/x, 1/x^2*y + (z4^2 + z4)/x] sage: D.dimension() 2 sage: f1, f2 = D.basis_function_space() [(x + z4)/x, 1/x^2*y + (z4^2 + z4)/x] sage: f1.zeros() [Place (x + z4, y^2 + (z4^3 + z4^2)*y + z4^2 + z4 + 1), Place (x + z4, y + z4^3 + z4^2)] sage: Q1, Q2 = _ sage: q1 = C.place_to_closed_point(Q1); q1 Point (y^2 + (z4^3 + z4^2)*y + (z4^2 + z4 + 1), x + (z4)) sage: q1.degree() 2 sage: q1 = C.place_to_closed_point(Q1); q1 Point (y^2 + (z4^3 + z4^2)*y + (z4^2 + z4 + 1), x + (z4)) sage: q1.degree() 2 sage: q2 = C.place_to_closed_point(Q2) sage: q2.degree() 1 sage: q2.rational_point() (z4, z4^3 + z4^2) sage: _ in C True
Puiseux series
After 11 years Trac #4618 has come to an end. Thus, Puiseux series are available, right now:
sage: R.<x> = PuiseuxSeriesRing(QQ) sage: p = x^(-7/2) + 3 + 5*x^(1/2) - 7*x^3 sage: 1/p x^(7/2) - 3*x^7 - 5*x^(15/2) + 7*x^10 + 9*x^(21/2) + 30*x^11 + 25*x^(23/2) + O(x^(27/2))
Localization
Integral domains can be localized at finite sets of their non invertible elements:
sage: L = ZZ.localization(45); L Integer Ring localized at (3, 5) sage: [1/l in L for l in range(1,6)] [True, False, True, False, True] sage: P.<x,y,z> = QQ[] sage: d = x^2+y^2+z^2 sage: Ld = P.localization(d); Ld Multivariate Polynomial Ring in x, y, z over Rational Field localized at (x^2 + y^2 + z^2,) sage: (x + y + z)/d in Ld True
Ariki–Koike algebras
An Ariki–Koike algebra (aka cyclotomic Hecke algebra) is a generalization of the Iwahori–Hecke algebra to the complex reflection group G(r,1,n) instead of a Coxeter group.
Graph theory
Arboricity
The arboricity of a graph can now be computed using the arboricity function (#19053).
MCS traversal and clique separators
Ticket #28473 introduced the following methods to the Graph class:
maximum_cardinality_search for the Maximal Cardinality Search (MCS) graph traversal (in O(n+m) time),
maximum_cardinality_search_M, an extension of MCS that also returns a minimal triangulation (in O(n.m) time), and
atoms_and_clique_separators, a method that decomposes the graph according clique minimal separators and returns the atoms and the clique minimal separators (in O(n.m) time).
Hypergraphs
Checking whether a uniform hypergraph has a Berge-cycle can be done using the is_berge_cyclic method of ticket #21931.
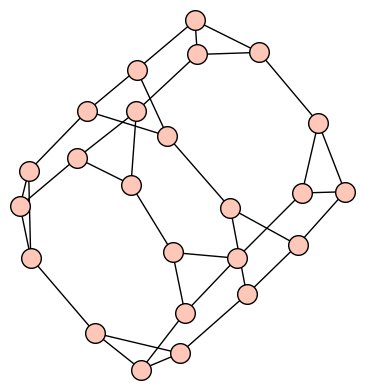
Generator for cube-connected cycles
There is now a generator for cube-connected cycles (#21423):
sage: g = graphs.CubeConnectedCycle(3) Cube-Connected Cycle of dimension 3: Graph on 24 vertices
Enumeration of minimal dominating sets
The minimal_dominating_sets method of a Graph is a generator of its minimal dominating sets (#27424):
Manifolds
Degenerate manifolds and submanifolds
Manifolds equipped with a degenerate metric have been introduced in this release. See the documentation and well as these Jupyter notebooks: example 1 and example 2
More functionatilities in index notation for tensors
Index notation to indicate operations like contractions has been enhanced. For instance, a sum can be introduced in a contraction:
Applying a function to all components of a tensor field
The new method apply_map() of tensor fields allows one to perform operations like factorization, expansion, simplification or substitution on all components of a tensor field:
Other changes
Some improvements and bug fixes have been introduced in this release. See the full change log.
Configuration changes
Easier installation of optional linear and mixed integer linear optimization backends
It is no longer necessary to recompile sagelib if you wish to use one of the state-of-the-art LP/MIP solvers COIN-OR CBC, CPLEX, or Gurobi, instead of the default (GLPK). The simplified new installation procedure is explained in the Thematic Tutorial on Linear Programming.
(If you cannot update to 9.1 just yet, you can retroactively get the same feature in your installation of Sage too by pip-installing one of the packages sage-numerical-backends-cplex, sage-numerical-backends-coin, sage-numerical-backends-gurobi.)
New way to install optional and experimental packages
It is now possible to use ./configure options to request the installation of optional and experimental packages at the next run of make. For example, type
$ ./configure --enable-4ti2 --enable-lrslib
to request these two packages to be installed. Check ./configure --help for a list of all options. (The traditional way of installing optional packages, sage -i, still works.)
Likewise, optional and experimental packages can be requested to be uninstalled at the next run of make by using --disable-SPKG options.
For developers and packagers
Happy news! The configuration file
src/bin/sage-env-config (installed as $SAGE_LOCAL/bin/sage-env-config)
(introduced 4 years ago in Trac #21479) finally has some company. Two new configuration files, also generated by the Sage distribution's ./configure script, are taking over some of its duties.
build/bin/sage-build-env-config (not installed) provides configuration variables that are used only while building packages.
build/pkgs/sage_conf/src/sage_conf.py (installed as Python module sage_conf) provides configuration variables that are needed by the Sage library runtime, but are not needed in the form of environment variables. (They are available to the Sage library even when it is imported into a Python running outside of the environment set up by sage-env.)
See Meta-ticket #21707: Split sage-env into 5 to clean up sage configuration for details and planned future work.
Spring cleaning
Trac #29636: Delete changelog sections from all SPKG information files; they were deprecated in favor of using Trac years ago. The contributions of Sage developers maintaining SPKGs are documented by our historical changelogs.
Trac #29406: Remove documentation on creating old-style SPKGs, Trac #29383: Remove related scripts
Remove numerous deprecated items, fix coding style, refactoring
Availability of Sage 9.1 and installation help
Sage 9.1 has not been released yet. See sage-release for announcements of beta versions and release candidates.
Availability in distributions
(TBD)
Installation FAQ
See sage-release, sage-devel.
