|
Size: 10175
Comment: summarize #7770
|
Size: 13292
Comment: summarize #6820
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 25: | Line 25: |
| * [[http://trac.sagemath.org/sage_trac/ticket/7754 | #7754]] (Nicolas M. Thiéry) | * Weyl group optimizations [[http://trac.sagemath.org/sage_trac/ticket/7754 | #7754]] (Nicolas M. Thiéry) --- Three major improvements that indirectly also improve efficiency of most Weyl group routines: * Faster hash method calling the hash of the underlying matrix (which is set as immutable for that purpose). * New `__eq__()` method. * Action on the weight lattice realization: optimization of the matrix multiplication. Some operations are now up to 34% faster than previously: {{{ BEFORE sage: W = WeylGroup(["F", 4]) sage: W.cardinality() 1152 sage: %time list(W); CPU times: user 10.51 s, sys: 0.05 s, total: 10.56 s Wall time: 10.56 s sage: W = WeylGroup(["E", 8]) sage: %time W.long_element(); CPU times: user 1.47 s, sys: 0.00 s, total: 1.47 s Wall time: 1.47 s AFTER sage: W = WeylGroup(["F", 4]) sage: W.cardinality() 1152 sage: %time list(W); CPU times: user 6.89 s, sys: 0.04 s, total: 6.93 s Wall time: 6.93 s sage: W = WeylGroup(["E", 8]) sage: %time W.long_element(); CPU times: user 1.21 s, sys: 0.00 s, total: 1.21 s Wall time: 1.21 s }}} |
| Line 140: | Line 172: |
| * [[http://trac.sagemath.org/sage_trac/ticket/5174 | #5174]] (John Palmieri) | * Viewing entries of large matrices [[http://trac.sagemath.org/sage_trac/ticket/5174 | #5174]] (John Palmieri) --- For a small matrix such as `2 x 2`, the default is to print the entries of the matrix. This default behaviour is unsuitable for large matrices such as `100 x 100`. The string representation of such large matrices now indicate how to view all their entries. Here are some examples illustrating the new way to view the string representation of matrices. If the matrix is too big, all the elements are not displayed by default: {{{ sage: A = random_matrix(ZZ, 5) sage: A [ 1 -4 -4 1 -1] [-1 1 13 -1 -1] [-1 0 0 -1 -1] [-8 1 -1 1 -4] [ 1 -5 -1 1 2] sage: A = random_matrix(ZZ, 100) sage: A 100 x 100 dense matrix over Integer Ring (type 'print A.str()' to see all of the entries) }}} If a matrix has several names, refer to the matrix as "obj": {{{ sage: A = random_matrix(ZZ, 200) sage: B = A sage: B 200 x 200 dense matrix over Integer Ring (type 'print obj.str()' to see all of the entries) }}} If a matrix doesn't have a name, don't print any name referring to the matrix in its string representation: {{{ sage: A = random_matrix(ZZ, 150) sage: A.transpose() 150 x 150 dense matrix over Integer Ring sage: T = A.transpose(); T 150 x 150 dense matrix over Integer Ring (type 'print T.str()' to see all of the entries) }}} |
| Line 147: | Line 207: |
| * [[http://trac.sagemath.org/sage_trac/ticket/6820 | #6820]] (John Palmieri, Mitesh Patel) | * Command line access to HTML documentation and docstrings [[http://trac.sagemath.org/sage_trac/ticket/6820 | #6820]] (John Palmieri, Mitesh Patel) --- Browse the Sage standard documentation from the command line or within the notebook interface. Use the following commands to browse documents in the standard documentation: * `browse_sage_doc.tutorial()` or its alias `tutorial()` * `browse_sage_doc.reference()`, or its aliases `reference()` and `manual()` * `browse_sage_doc.developer()` or its alias `developer()` * `browse_sage_doc.constructions()` or its alias `constructions()` The following screenshot illustrates viewing the Sage tutorial from the command line interface, activated using the command: {{{ sage: tutorial() }}} This command invoked a terminal-based web browser such as Links to view the tutorial. {{attachment:browse-doc-cmd.png}} |
Sage 4.3.1 Release Tour
Major features
Substantial work towards a complete SPARC Solaris 10 port. This is due to the hard work of David Kirkby. The relevant tickets include #6595, #7138, #7162, #7505, #7817.
We're moving closer towards a FreeBSD port, thanks to the work of Peter Jeremy at ticket #7825.
Basic arithmetics
Implement conjugate() for RealDoubleElement #7834 (Dag Sverre Seljebotn) --- New method conjugate() in the class RealDoubleElement of the module sage/rings/real_double.pyx for returning the complex conjugate of a real number. This is consistent with conjugate() methods in ZZ and RR. For example,
sage: ZZ(5).conjugate() 5 sage: RR(5).conjugate() 5.00000000000000 sage: RDF(5).conjugate() 5.0
Combinatorics
Weyl group optimizations #7754 (Nicolas M. Thiéry) --- Three major improvements that indirectly also improve efficiency of most Weyl group routines:
- Faster hash method calling the hash of the underlying matrix (which is set as immutable for that purpose).
New __eq__() method.
- Action on the weight lattice realization: optimization of the matrix multiplication.
BEFORE sage: W = WeylGroup(["F", 4]) sage: W.cardinality() 1152 sage: %time list(W); CPU times: user 10.51 s, sys: 0.05 s, total: 10.56 s Wall time: 10.56 s sage: W = WeylGroup(["E", 8]) sage: %time W.long_element(); CPU times: user 1.47 s, sys: 0.00 s, total: 1.47 s Wall time: 1.47 s AFTER sage: W = WeylGroup(["F", 4]) sage: W.cardinality() 1152 sage: %time list(W); CPU times: user 6.89 s, sys: 0.04 s, total: 6.93 s Wall time: 6.93 s sage: W = WeylGroup(["E", 8]) sage: %time W.long_element(); CPU times: user 1.21 s, sys: 0.00 s, total: 1.21 s Wall time: 1.21 s
Elliptic curves
Two-isogeny descent over QQ natively using ratpoints #6583 (Robert Miller) --- New module sage/schemes/elliptic_curves/descent_two_isogeny.pyx for descent on elliptic curves over QQ with a 2-isogeny. The relevant user interface function is two_descent_by_two_isogeny() that takes an elliptic curve E with a two-isogeny phi : E --> E' and dual isogeny phi', runs a two-isogeny descent on E, and returns n1, n2, n1' and n2'. Here, n1 is the number of quartic covers found with a rational point and n2 is the number which are ELS. Here are some examples illustrating the use of two_descent_by_two_isogeny():
sage: from sage.schemes.elliptic_curves.descent_two_isogeny import two_descent_by_two_isogeny sage: E = EllipticCurve("14a") sage: n1, n2, n1_prime, n2_prime = two_descent_by_two_isogeny(E) sage: log(n1, 2) + log(n1_prime, 2) - 2 # the rank 0 sage: E = EllipticCurve("65a") sage: n1, n2, n1_prime, n2_prime = two_descent_by_two_isogeny(E) sage: log(n1, 2) + log(n1_prime, 2) - 2 # the rank 1 sage: E = EllipticCurve("1088j1") sage: n1, n2, n1_prime, n2_prime = two_descent_by_two_isogeny(E) sage: log(n1, 2) + log(n1_prime, 2) - 2 # the rank 2You could also ask two_descent_by_two_isogeny() to be verbose in its computation:
sage: E = EllipticCurve("14a") sage: two_descent_by_two_isogeny(E, verbosity=1) 2-isogeny Results: 2 <= #E(Q)/phi'(E'(Q)) <= 2 2 <= #E'(Q)/phi(E(Q)) <= 2 #Sel^(phi')(E'/Q) = 2 #Sel^(phi)(E/Q) = 2 1 <= #Sha(E'/Q)[phi'] <= 1 1 <= #Sha(E/Q)[phi] <= 1 1 <= #Sha(E/Q)[2], #Sha(E'/Q)[2] <= 1 0 <= rank of E(Q) = rank of E'(Q) <= 0 (2, 2, 2, 2)More functions for elliptic curve isogenies #6887 (John Cremona, Jenny Cooley) --- Code for constructing elliptic curve isogenies already existed in Sage 4.1.1. The enhancements here include:
For l=2,3,5,7,13 over any field, find all l-isogenies of a given elliptic curve. (These are the l for which X_0(l) has genus 0).
Similarly for the remaining l for which l-isogenies exist over QQ.
Given an elliptic curve over QQ, find the whole isogeny class in a robust manner.
Testing if two curves are isogenous at least over QQ.
The relevant use interface method is isogenies_prime_degree() in the class EllipticCurve_field of the module sage/schemes/elliptic_curves/ell_field.py. Here are some examples showing isogenies_prime_degree() in action. Examples over finite fields:
sage: E = EllipticCurve(GF(next_prime(1000000)), [7,8]) sage: E.isogenies_prime_degree() [Isogeny of degree 2 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 970389*x + 794257 over Finite Field of size 1000003, Isogeny of degree 2 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 29783*x + 206196 over Finite Field of size 1000003, Isogeny of degree 2 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 999960*x + 78 over Finite Field of size 1000003, Isogeny of degree 13 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 878063*x + 845666 over Finite Field of size 1000003, Isogeny of degree 13 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 375648*x + 342776 over Finite Field of size 1000003] sage: E.isogenies_prime_degree(13) [Isogeny of degree 13 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 878063*x + 845666 over Finite Field of size 1000003, Isogeny of degree 13 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 375648*x + 342776 over Finite Field of size 1000003]
Examples over number fields (other than QQ):
sage: QQroot2.<e> = NumberField(x^2 - 2) sage: E = EllipticCurve(QQroot2, [1,0,1,4,-6]) sage: E.isogenies_prime_degree(2) [Isogeny of degree 2 from Elliptic Curve defined by y^2 + x*y + y = x^3 + 4*x + (-6) over Number Field in e with defining polynomial x^2 - 2 to Elliptic Curve defined by y^2 + x*y + y = x^3 + (-36)*x + (-70) over Number Field in e with defining polynomial x^2 - 2] sage: E.isogenies_prime_degree(3) [Isogeny of degree 3 from Elliptic Curve defined by y^2 + x*y + y = x^3 + 4*x + (-6) over Number Field in e with defining polynomial x^2 - 2 to Elliptic Curve defined by y^2 + x*y + y = x^3 + (-171)*x + (-874) over Number Field in e with defining polynomial x^2 - 2, Isogeny of degree 3 from Elliptic Curve defined by y^2 + x*y + y = x^3 + 4*x + (-6) over Number Field in e with defining polynomial x^2 - 2 to Elliptic Curve defined by y^2 + x*y + y = x^3 + (-128/3)*x + 5662/27 over Number Field in e with defining polynomial x^2 - 2]
Graph theory
An interactive graph editor #1321 (Radoslav Kirov, Mitesh Patel) --- Embed an interactive graph editor into the notebook. The following screenshot shows a graph editor for playing around with the complete graph on 5 vertices:
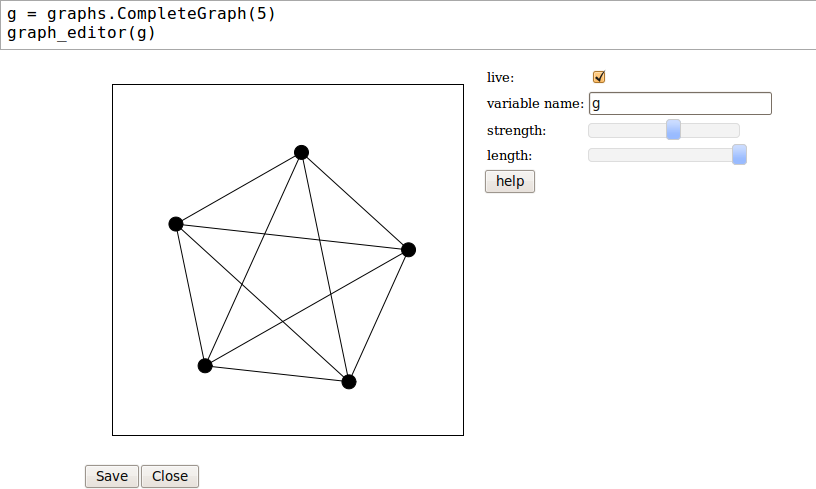
Breadth/depth first searches and basic connectivity for c_graphs #7724 (Nathann Cohen, Yann Laigle-Chapuy) --- Implementation of the following methods for the class CGraphBackend in the module sage/graphs/base/c_graph.pyx:
depth_first_search()
breadth_first_search()
is_connected()
is_strongly_connected()
sage: g = graphs.RandomGNP(1000, 0.01) sage: h = g.copy(implementation="c_graph") sage: %timeit list(g.depth_first_search(0)); 100 loops, best of 3: 8.17 ms per loop sage: %timeit list(h.depth_first_search(0)); 100 loops, best of 3: 3.29 ms per loop sage: sage: %timeit list(g.breadth_first_search(0)); 100 loops, best of 3: 6.48 ms per loop sage: %timeit list(h.breadth_first_search(0)); 10 loops, best of 3: 34 ms per loop sage: sage: %timeit g.is_connected(); 100 loops, best of 3: 8.47 ms per loop sage: %timeit h.is_connected(); 100 loops, best of 3: 3.41 ms per loop sage: sage: g = g.to_directed() sage: h = g.copy(implementation="c_graph") sage: %timeit g.is_strongly_connected(); 10 loops, best of 3: 23.5 ms per loop sage: %timeit h.is_strongly_connected(); 10 loops, best of 3: 25 ms per loop
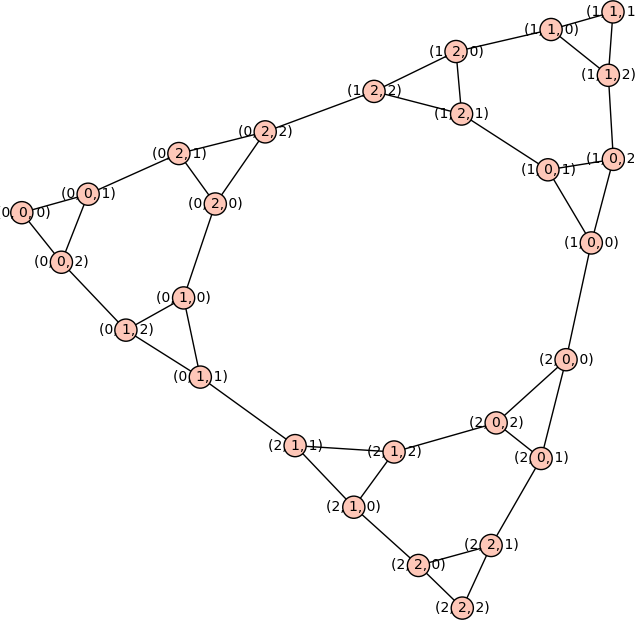
Tower of Hanoi graph #7770 (Rob Beezer) --- The Tower of Hanoi puzzle can be described by a graph whose vertices are possible states of the disks on the pegs, with edges representing legitimate moves of a single disk. The new method HanoiTowerGraph() of the class GraphGenerators in the module sage/graphs/graph_generators.py returns the graph whose vertices are the states of the Tower of Hanoi puzzle, with edges representing legal moves between states. See the documentation of this method for details on interpreting the the possible states of this puzzle. The following screenshot shows all the possible states of an instance of the puzzle with 3 pegs and 3 disks, produced using the following code:
H = graphs.HanoiTowerGraph(3, 3, positions=False) show(H, figsize=[8,8])
Linear algebra
Viewing entries of large matrices #5174 (John Palmieri) --- For a small matrix such as 2 x 2, the default is to print the entries of the matrix. This default behaviour is unsuitable for large matrices such as 100 x 100. The string representation of such large matrices now indicate how to view all their entries. Here are some examples illustrating the new way to view the string representation of matrices. If the matrix is too big, all the elements are not displayed by default:
sage: A = random_matrix(ZZ, 5) sage: A [ 1 -4 -4 1 -1] [-1 1 13 -1 -1] [-1 0 0 -1 -1] [-8 1 -1 1 -4] [ 1 -5 -1 1 2] sage: A = random_matrix(ZZ, 100) sage: A 100 x 100 dense matrix over Integer Ring (type 'print A.str()' to see all of the entries)
If a matrix has several names, refer to the matrix as "obj":sage: A = random_matrix(ZZ, 200) sage: B = A sage: B 200 x 200 dense matrix over Integer Ring (type 'print obj.str()' to see all of the entries)
If a matrix doesn't have a name, don't print any name referring to the matrix in its string representation:sage: A = random_matrix(ZZ, 150) sage: A.transpose() 150 x 150 dense matrix over Integer Ring sage: T = A.transpose(); T 150 x 150 dense matrix over Integer Ring (type 'print T.str()' to see all of the entries)
#7728 (Dag Sverre Seljebotn)
Miscellaneous
Command line access to HTML documentation and docstrings #6820 (John Palmieri, Mitesh Patel) --- Browse the Sage standard documentation from the command line or within the notebook interface. Use the following commands to browse documents in the standard documentation:
browse_sage_doc.tutorial() or its alias tutorial()
browse_sage_doc.reference(), or its aliases reference() and manual()
browse_sage_doc.developer() or its alias developer()
browse_sage_doc.constructions() or its alias constructions()
sage: tutorial()
This command invoked a terminal-based web browser such as Links to view the tutorial.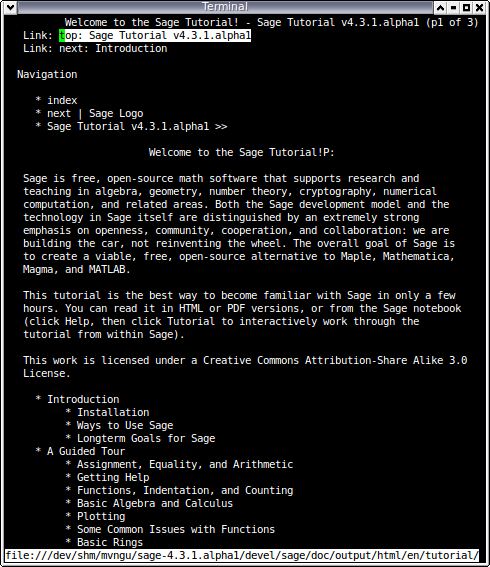
#7482 (William Stein)
#7514 (William Stein)
