|
Size: 8114
Comment: summarize #1321
|
Size: 9351
Comment: summarize #7724
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 94: | Line 94: |
| * [[http://trac.sagemath.org/sage_trac/ticket/7724 | #7724]] (Nathann Cohen, Yann Laigle-Chapuy) | * Breadth/depth first searches and basic connectivity for c_graphs [[http://trac.sagemath.org/sage_trac/ticket/7724 | #7724]] (Nathann Cohen, Yann Laigle-Chapuy) --- Implementation of the following methods for the class `CGraphBackend` in the module `sage/graphs/base/c_graph.pyx`: * `depth_first_search()` * `breadth_first_search()` * `is_connected()` * `is_strongly_connected()` In some cases, the c_graphs implementation of these methods provides a 2x speed improvement: {{{ sage: g = graphs.RandomGNP(1000, 0.01) sage: h = g.copy(implementation="c_graph") sage: %timeit list(g.depth_first_search(0)); 100 loops, best of 3: 8.17 ms per loop sage: %timeit list(h.depth_first_search(0)); 100 loops, best of 3: 3.29 ms per loop sage: sage: %timeit list(g.breadth_first_search(0)); 100 loops, best of 3: 6.48 ms per loop sage: %timeit list(h.breadth_first_search(0)); 10 loops, best of 3: 34 ms per loop sage: sage: %timeit g.is_connected(); 100 loops, best of 3: 8.47 ms per loop sage: %timeit h.is_connected(); 100 loops, best of 3: 3.41 ms per loop sage: sage: g = g.to_directed() sage: h = g.copy(implementation="c_graph") sage: %timeit g.is_strongly_connected(); 10 loops, best of 3: 23.5 ms per loop sage: %timeit h.is_strongly_connected(); 10 loops, best of 3: 25 ms per loop }}} |
Sage 4.3.1 Release Tour
Major features
Substantial work towards a complete SPARC Solaris 10 port. This is due to the hard work of David Kirkby. The relevant tickets include #6595, #7138, #7162, #7505, #7817.
We're moving closer towards a FreeBSD port, thanks to the work of Peter Jeremy at ticket #7825.
Basic arithmetics
Implement conjugate() for RealDoubleElement #7834 (Dag Sverre Seljebotn) --- New method conjugate() in the class RealDoubleElement of the module sage/rings/real_double.pyx for returning the complex conjugate of a real number. This is consistent with conjugate() methods in ZZ and RR. For example,
sage: ZZ(5).conjugate() 5 sage: RR(5).conjugate() 5.00000000000000 sage: RDF(5).conjugate() 5.0
Combinatorics
#7754 (Nicolas M. Thiéry)
Elliptic curves
Two-isogeny descent over QQ natively using ratpoints #6583 (Robert Miller) --- New module sage/schemes/elliptic_curves/descent_two_isogeny.pyx for descent on elliptic curves over QQ with a 2-isogeny. The relevant user interface function is two_descent_by_two_isogeny() that takes an elliptic curve E with a two-isogeny phi : E --> E' and dual isogeny phi', runs a two-isogeny descent on E, and returns n1, n2, n1' and n2'. Here, n1 is the number of quartic covers found with a rational point and n2 is the number which are ELS. Here are some examples illustrating the use of two_descent_by_two_isogeny():
sage: from sage.schemes.elliptic_curves.descent_two_isogeny import two_descent_by_two_isogeny sage: E = EllipticCurve("14a") sage: n1, n2, n1_prime, n2_prime = two_descent_by_two_isogeny(E) sage: log(n1, 2) + log(n1_prime, 2) - 2 # the rank 0 sage: E = EllipticCurve("65a") sage: n1, n2, n1_prime, n2_prime = two_descent_by_two_isogeny(E) sage: log(n1, 2) + log(n1_prime, 2) - 2 # the rank 1 sage: E = EllipticCurve("1088j1") sage: n1, n2, n1_prime, n2_prime = two_descent_by_two_isogeny(E) sage: log(n1, 2) + log(n1_prime, 2) - 2 # the rank 2You could also ask two_descent_by_two_isogeny() to be verbose in its computation:
sage: E = EllipticCurve("14a") sage: two_descent_by_two_isogeny(E, verbosity=1) 2-isogeny Results: 2 <= #E(Q)/phi'(E'(Q)) <= 2 2 <= #E'(Q)/phi(E(Q)) <= 2 #Sel^(phi')(E'/Q) = 2 #Sel^(phi)(E/Q) = 2 1 <= #Sha(E'/Q)[phi'] <= 1 1 <= #Sha(E/Q)[phi] <= 1 1 <= #Sha(E/Q)[2], #Sha(E'/Q)[2] <= 1 0 <= rank of E(Q) = rank of E'(Q) <= 0 (2, 2, 2, 2)More functions for elliptic curve isogenies #6887 (John Cremona, Jenny Cooley) --- Code for constructing elliptic curve isogenies already existed in Sage 4.1.1. The enhancements here include:
For l=2,3,5,7,13 over any field, find all l-isogenies of a given elliptic curve. (These are the l for which X_0(l) has genus 0).
Similarly for the remaining l for which l-isogenies exist over QQ.
Given an elliptic curve over QQ, find the whole isogeny class in a robust manner.
Testing if two curves are isogenous at least over QQ.
The relevant use interface method is isogenies_prime_degree() in the class EllipticCurve_field of the module sage/schemes/elliptic_curves/ell_field.py. Here are some examples showing isogenies_prime_degree() in action. Examples over finite fields:
sage: E = EllipticCurve(GF(next_prime(1000000)), [7,8]) sage: E.isogenies_prime_degree() [Isogeny of degree 2 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 970389*x + 794257 over Finite Field of size 1000003, Isogeny of degree 2 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 29783*x + 206196 over Finite Field of size 1000003, Isogeny of degree 2 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 999960*x + 78 over Finite Field of size 1000003, Isogeny of degree 13 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 878063*x + 845666 over Finite Field of size 1000003, Isogeny of degree 13 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 375648*x + 342776 over Finite Field of size 1000003] sage: E.isogenies_prime_degree(13) [Isogeny of degree 13 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 878063*x + 845666 over Finite Field of size 1000003, Isogeny of degree 13 from Elliptic Curve defined by y^2 = x^3 + 7*x + 8 over Finite Field of size 1000003 to Elliptic Curve defined by y^2 = x^3 + 375648*x + 342776 over Finite Field of size 1000003]
Examples over number fields (other than QQ):
sage: QQroot2.<e> = NumberField(x^2 - 2) sage: E = EllipticCurve(QQroot2, [1,0,1,4,-6]) sage: E.isogenies_prime_degree(2) [Isogeny of degree 2 from Elliptic Curve defined by y^2 + x*y + y = x^3 + 4*x + (-6) over Number Field in e with defining polynomial x^2 - 2 to Elliptic Curve defined by y^2 + x*y + y = x^3 + (-36)*x + (-70) over Number Field in e with defining polynomial x^2 - 2] sage: E.isogenies_prime_degree(3) [Isogeny of degree 3 from Elliptic Curve defined by y^2 + x*y + y = x^3 + 4*x + (-6) over Number Field in e with defining polynomial x^2 - 2 to Elliptic Curve defined by y^2 + x*y + y = x^3 + (-171)*x + (-874) over Number Field in e with defining polynomial x^2 - 2, Isogeny of degree 3 from Elliptic Curve defined by y^2 + x*y + y = x^3 + 4*x + (-6) over Number Field in e with defining polynomial x^2 - 2 to Elliptic Curve defined by y^2 + x*y + y = x^3 + (-128/3)*x + 5662/27 over Number Field in e with defining polynomial x^2 - 2]
Graph theory
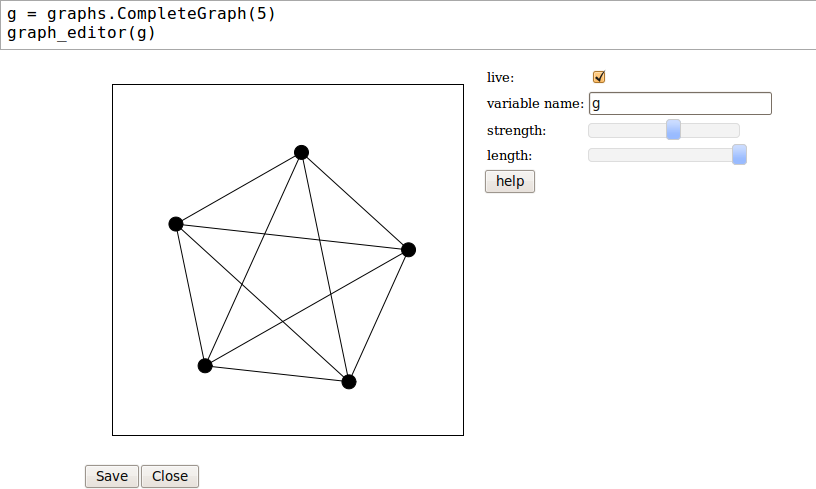
An interactive graph editor #1321 (Radoslav Kirov, Mitesh Patel) --- Embed an interactive graph editor into the notebook. The following screenshot shows a graph editor for playing around with the complete graph on 5 vertices:
Breadth/depth first searches and basic connectivity for c_graphs #7724 (Nathann Cohen, Yann Laigle-Chapuy) --- Implementation of the following methods for the class CGraphBackend in the module sage/graphs/base/c_graph.pyx:
depth_first_search()
breadth_first_search()
is_connected()
is_strongly_connected()
sage: g = graphs.RandomGNP(1000, 0.01) sage: h = g.copy(implementation="c_graph") sage: %timeit list(g.depth_first_search(0)); 100 loops, best of 3: 8.17 ms per loop sage: %timeit list(h.depth_first_search(0)); 100 loops, best of 3: 3.29 ms per loop sage: sage: %timeit list(g.breadth_first_search(0)); 100 loops, best of 3: 6.48 ms per loop sage: %timeit list(h.breadth_first_search(0)); 10 loops, best of 3: 34 ms per loop sage: sage: %timeit g.is_connected(); 100 loops, best of 3: 8.47 ms per loop sage: %timeit h.is_connected(); 100 loops, best of 3: 3.41 ms per loop sage: sage: g = g.to_directed() sage: h = g.copy(implementation="c_graph") sage: %timeit g.is_strongly_connected(); 10 loops, best of 3: 23.5 ms per loop sage: %timeit h.is_strongly_connected(); 10 loops, best of 3: 25 ms per loop
#7770 (Rob Beezer)
Linear algebra
Miscellaneous
