|
Size: 5622
Comment:
|
Size: 14180
Comment: Summarize #6164
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 1: | Line 1: |
| Line 3: | Line 4: |
| Sage 4.1 was released on FIXME. For the official, comprehensive release note, please refer to FIXME. A nicely formatted version of this release tour can be found at FIXME. The following points are some of the foci of this release: * == Algebra == * FIXME: summarize #6362 |
Sage 4.1 was released on July 09, 2009. For the official, comprehensive release note, please refer to [[http://www.sagemath.org/src/announce/sage-4.1.txt|sage-4.1.txt]]. A nicely formatted version of this release tour can be found at FIXME. The following points are some of the foci of this release: * Upgrade to Python 2.6.x * Support for building Singular with GCC 4.4 * Optimized integer division * Combinatorics: irreducible matrix representations of symmetric groups; and Yang-Baxter Graphs * Cryptography: Mini Advanced Encryption Standard for educational purposes * Graph theory: back-end for graph theory with Cython (c_graph); and improve accuracy of graph eigenvalues * Linear algebra: a general package for finitely generated, not-necessarily free R-modules; and multiplicative order for matrices over finite fields * Miscellaneous: optimized Sudoku solver; a decorator for declaring abstract methods; and support Unicode in LaTeX cells (notebook) * Number theory: improved random element generation for number field orders and ideals; support Michael Stoll's ratpoints package; and elliptic exponential * Numerical: computing numerical values of constants using mpmath * Update, upgrade 18 packages to latest upstream releases |
| Line 17: | Line 22: |
| * FIXME: summarize #4290 | * Construct an elliptic curve from a plane curve of genus one (Lloyd Kilford, John Cremona ) -- New function {{{EllipticCurve_from_plane_curve()}}} in the module {{{sage/schemes/elliptic_curves/constructor.py}}} to allow the construction of an elliptic curve from a smooth plane cubic with a rational point. Currently, this function uses Magma and it will not work on machines that do not have Magma installed. Assuming you have Magma installed on your computer, we can use the function {{{EllipticCurve_from_plane_curve()}}} to first check that the Fermat cubic is isomorphic to the curve with Cremona label "27a1": {{{#!python numbers=off sage: x, y, z = PolynomialRing(QQ, 3, 'xyz').gens() # optional - magma sage: C = Curve(x^3 + y^3 + z^3) # optional - magma sage: P = C(1, -1, 0) # optional - magma sage: E = EllipticCurve_from_plane_curve(C, P) # optional - magma sage: E # optional - magma Elliptic Curve defined by y^2 + y = x^3 - 7 over Rational Field sage: E.label() # optional - magma '27a1' }}} Here is a quartic example: {{{#!python numbers=off sage: u, v, w = PolynomialRing(QQ, 3, 'uvw').gens() # optional - magma sage: C = Curve(u^4 + u^2*v^2 - w^4) # optional - magma sage: P = C(1, 0, 1) # optional - magma sage: E = EllipticCurve_from_plane_curve(C, P) # optional - magma sage: E # optional - magma Elliptic Curve defined by y^2 = x^3 + 4*x over Rational Field sage: E.label() # optional - magma '32a1' }}} |
| Line 23: | Line 49: |
| * FIXME: summarize #6083 | * Speed-up integer division (Robert Bradshaw ) -- In some cases, integer division is now up to 31% faster than previously. The following timing statistics were obtained using the machine sage.math: {{{#!python numbers=off # BEFORE sage: a = next_prime(2**31) sage: b = Integers(a)(100) sage: %timeit a % b; 1000000 loops, best of 3: 1.12 µs per loop sage: %timeit 101 // int(5); 1000000 loops, best of 3: 215 ns per loop sage: %timeit 100 // int(-3) 1000000 loops, best of 3: 214 ns per loop sage: a = ZZ.random_element(10**50) sage: b = ZZ.random_element(10**15) sage: %timeit a.quo_rem(b) 1000000 loops, best of 3: 454 ns per loop # AFTER sage: a = next_prime(2**31) sage: b = Integers(a)(100) sage: %timeit a % b; 1000000 loops, best of 3: 1.02 µs per loop sage: %timeit 101 // int(5); 1000000 loops, best of 3: 201 ns per loop sage: %timeit 100 // int(-3) 1000000 loops, best of 3: 194 ns per loop sage: a = ZZ.random_element(10**50) sage: b = ZZ.random_element(10**15) sage: %timeit a.quo_rem(b) 1000000 loops, best of 3: 313 ns per loop }}} |
| Line 28: | Line 86: |
| 1. '''Irreducible matrix representations of symmetric groups (Ticket #5878)'''. FrancoSaliola, based on the [[http://www-igm.univ-mlv.fr/~al|Alain Lascoux]] article [[http://phalanstere.univ-mlv.fr/~al/ARTICLES/ProcCrac.ps.gz|Young representations of the symmetric group]], added support for constructing irreducible representations of the symmetric group. Three types of representations have been implemented. * '''Specht representations'''. The matrices have integer entries. {{{ sage: chi = SymmetricGroupRepresentation([3,2]) |
* Irreducible matrix representations of symmetric groups (Franco Saliola) -- Support for constructing irreducible representations of the symmetric group. This is based on [[http://www-igm.univ-mlv.fr/~al|Alain Lascoux's]] article [[http://phalanstere.univ-mlv.fr/~al/ARTICLES/ProcCrac.ps.gz|Young representations of the symmetric group]]. The following types of representations are supported: * Specht representations -- The matrices have integer entries: {{{#!python numbers=off sage: chi = SymmetricGroupRepresentation([3, 2]); chi |
| Line 38: | Line 92: |
sage: chi([5,4,3,2,1]) |
sage: chi([5, 4, 3, 2, 1]) |
| Line 47: | Line 101: |
| * '''Young's seminormal representation'''. The matrices have rational entries. {{{ sage: snorm = SymmetricGroupRepresentation([2,1], "seminormal") sage: snorm |
* Young's seminormal representation -- The matrices have rational entries: {{{#!python numbers=off sage: snorm = SymmetricGroupRepresentation([2, 1], "seminormal"); snorm |
| Line 52: | Line 105: |
sage: snorm([1,3,2]) |
sage: snorm([1, 3, 2]) |
| Line 58: | Line 111: |
| * '''Young's orthogonal representation''' (the matrices are orthogonal). These matrices are defined over Sage's {{{Symbolic Ring}}}. {{{ sage: ortho = SymmetricGroupRepresentation([3,2], "orthogonal") sage: ortho |
* Young's orthogonal representation (the matrices are orthogonal) -- These matrices are defined over Sage's {{{Symbolic Ring}}}: {{{#!python numbers=off sage: ortho = SymmetricGroupRepresentation([3, 2], "orthogonal"); ortho |
| Line 63: | Line 115: |
sage: ortho([1,3,2,4,5]) |
sage: ortho([1, 3, 2, 4, 5]) |
| Line 72: | Line 124: |
| One can also create the {{{CombinatorialClass}}} of all irreducible matrix representations of a given symmetric group. Then particular representations can be created by providing partitions. For example: {{{ sage: chi = SymmetricGroupRepresentations(5) sage: chi |
You can also create the {{{CombinatorialClass}}} of all irreducible matrix representations of a given symmetric group. Then particular representations can be created by providing partitions. For example: {{{#!python numbers=off sage: chi = SymmetricGroupRepresentations(5); chi |
| Line 78: | Line 128: |
| Line 81: | Line 130: |
| sage: chi([5])([2,1,3,4,5]) | sage: chi([5])([2, 1, 3, 4, 5]) |
| Line 83: | Line 132: |
sage: chi([1,1,1,1,1]) # the sign representation |
sage: chi([1, 1, 1, 1, 1]) # the sign representation |
| Line 86: | Line 134: |
| sage: chi([1,1,1,1,1])([2,1,3,4,5]) | sage: chi([1, 1, 1, 1, 1])([2, 1, 3, 4, 5]) |
| Line 88: | Line 136: |
sage: chi([3,2]) |
sage: chi([3, 2]) |
| Line 91: | Line 138: |
| sage: chi([3,2])([5,4,3,2,1]) | sage: chi([3, 2])([5, 4, 3, 2, 1]) |
| Line 98: | Line 146: |
See the documentation {{{SymmetricGroupRepresentation?}}} and {{{SymmetricGroupRepresentations?}}} for more information and examples. 1. '''Yang-Baxter Graphs (Ticket #5878)'''. Ticket #5878 (irreducible matrix representations of the symmetric group) also introduced support for Yang-Baxter graphs. Besides being used for constructing those representations, they can also be used to construct the Cayley graph of a finite group: {{{ |
See the documentation of {{{SymmetricGroupRepresentation}}} and {{{SymmetricGroupRepresentations}}} for more information and examples. * Yang-Baxter graphs (Franco Saliola) -- Besides being used for constructing the irreducible matrix representations of the symmetric group, Yang-Baxter graphs can also be used to construct the Cayley graph of a finite group. For example: {{{#!python numbers=off |
| Line 109: | Line 151: |
| ... return lambda h : h*g | ....: return lambda h : h*g ....: |
| Line 117: | Line 159: |
and to construct the permutahedron: {{{ |
{{attachment:cayley-graph.png}} Yang-Baxter graphs can also be used to construct the permutahedron: {{{#!python numbers=off |
| Line 126: | Line 168: |
See the documentation {{{YangBaxterGraph?}}} for more information and examples. == Commutative Algebra == |
{{attachment:permutahedron.png}} See the documentation of {{{YangBaxterGraph}}} for more information and examples. |
| Line 137: | Line 175: |
| * FIXME: summarize #6164 | * Mini Advanced Encryption Standard for educational purposes (Minh Van Nguyen) -- New module {{{sage/crypto/block_cipher/miniaes.py}}} to support the Mini Advanced Encryption Standard (Mini-AES) to allow students to explore the working of a block cipher. This is a simplified variant of the Advanced Encryption Standard (AES) to be used for cryptography education. Mini-AES is described in the paper: * A. C.-W. Phan. Mini advanced encryption standard (mini-AES): a testbed for cryptanalysis students. Cryptologia, 26(4):283--306, 2002. We can encrypt a plaintext using Mini-AES as follows: {{{#!python numbers=off sage: from sage.crypto.block_cipher.miniaes import MiniAES sage: maes = MiniAES() sage: K = FiniteField(16, "x") sage: MS = MatrixSpace(K, 2, 2) sage: P = MS([K("x^3 + x"), K("x^2 + 1"), K("x^2 + x"), K("x^3 + x^2")]); P [ x^3 + x x^2 + 1] [ x^2 + x x^3 + x^2] sage: key = MS([K("x^3 + x^2"), K("x^3 + x"), K("x^3 + x^2 + x"), K("x^2 + x + 1")]); key [ x^3 + x^2 x^3 + x] [x^3 + x^2 + x x^2 + x + 1] sage: C = maes.encrypt(P, key); C [ x x^2 + x] [x^3 + x^2 + x x^3 + x] }}} Here is the decryption process: {{{#!python numbers=off sage: plaintxt = maes.decrypt(C, key) sage: plaintxt == P True }}} We can also work directly with binary strings: {{{#!python numbers=off sage: from sage.crypto.block_cipher.miniaes import MiniAES sage: maes = MiniAES() sage: bin = BinaryStrings() sage: key = bin.encoding("KE"); key 0100101101000101 sage: P = bin.encoding("Encrypt this secret message!") sage: C = maes(P, key, algorithm="encrypt") sage: plaintxt = maes(C, key, algorithm="decrypt") sage: plaintxt == P True }}} Or work with integers {{{n}}} such that {{{0 <= n <= 15}}}: {{{#!python numbers=off sage: from sage.crypto.block_cipher.miniaes import MiniAES sage: maes = MiniAES() sage: P = [n for n in xrange(16)]; P [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15] sage: key = [2, 3, 11, 0]; key [2, 3, 11, 0] sage: P = maes.integer_to_binary(P) sage: key = maes.integer_to_binary(key) sage: C = maes(P, key, algorithm="encrypt") sage: plaintxt = maes(C, key, algorithm="decrypt") sage: plaintxt == P True }}} |
| Line 146: | Line 240: |
| * FIXME: summarize #6085 * FIXME: summarize #6258 |
1. FIXME: summarize #6085 1. '''Improve accuracy of graph eigenvalues (Ticket #6258)''', Rob Beezer. New routines compute eigenvalues and eigenvectors of integer matrices more precisely than before. Rather than convert adjacency matrices of graphs to computations over the reals or complexes, this patch retains adjacency matrices as matrices over the integers, yielding more accurate and informative results for eigenvalues, eigenvectors, and eigenspaces. * Examples follow for a circuit on 8 vertices: {{{#!python numbers=off g = graphs.CycleGraph(8) }}} * Integer eigenvalues are exact, irrational eigenvalues are more precise, making multiplicities easier to determine. {{{#!python numbers=off sage: g.spectrum() [2, 1.414213562373095?, 1.414213562373095?, 0, 0, -1.414213562373095?, -1.414213562373095?, -2] }}} * Similar comments apply to eigenvectors. {{{#!python numbers=off sage: g.eigenvectors() [(2, [ (1, 1, 1, 1, 1, 1, 1, 1) ], 1), (-2, [ (1, -1, 1, -1, 1, -1, 1, -1) ], 1), (0, [ (1, 0, -1, 0, 1, 0, -1, 0), (0, 1, 0, -1, 0, 1, 0, -1) ], 2), (-1.414213562373095?, [(1, 0, -1, 1.414213562373095?, -1, 0, 1, -1.414213562373095?), (0, 1, -1.414213562373095?, 1, 0, -1, 1.414213562373095?, -1)], 2), (1.414213562373095?, [(1, 0, -1, -1.414213562373095?, -1, 0, 1, 1.414213562373095?), (0, 1, 1.414213562373095?, 1, 0, -1, -1.414213562373095?, -1)], 2)] }}} * Eigenspaces are exact, in that they can be expressed as vector spaces over number fields. When the defining polynomial has several roots, the eigenspaces are not repeated. Previously eigenspaces were "fractured" owing to slight computational differences in identical eigenvalues. In concert with {{{eigenvectors()}}} this command illuminates the structure of a graph's eigenspaces more than purely numerical results. {{{#!python numbers=off sage: g.eigenspaces() [ (2, Vector space of degree 8 and dimension 1 over Rational Field User basis matrix: [1 1 1 1 1 1 1 1]), (-2, Vector space of degree 8 and dimension 1 over Rational Field User basis matrix: [ 1 -1 1 -1 1 -1 1 -1]), (0, Vector space of degree 8 and dimension 2 over Rational Field User basis matrix: [ 1 0 -1 0 1 0 -1 0] [ 0 1 0 -1 0 1 0 -1]), (a3, Vector space of degree 8 and dimension 2 over Number Field in a3 with defining polynomial x^2 - 2 User basis matrix: [ 1 0 -1 -a3 -1 0 1 a3] [ 0 1 a3 1 0 -1 -a3 -1]) }}} * Complex eigenvalues (of digraphs) previously were missing their imaginary parts. This bug has been fixed as part of this ticket. |
| Line 206: | Line 361: |
* Upgrade [[http://www.singular.uni-kl.de|Singular]] to version singular-3-1-0-2-20090620 with support for compiling with GCC 4.4. |
Sage 4.1 Release Tour
Sage 4.1 was released on July 09, 2009. For the official, comprehensive release note, please refer to sage-4.1.txt. A nicely formatted version of this release tour can be found at FIXME. The following points are some of the foci of this release:
- Upgrade to Python 2.6.x
- Support for building Singular with GCC 4.4
- Optimized integer division
- Combinatorics: irreducible matrix representations of symmetric groups; and Yang-Baxter Graphs
- Cryptography: Mini Advanced Encryption Standard for educational purposes
- Graph theory: back-end for graph theory with Cython (c_graph); and improve accuracy of graph eigenvalues
- Linear algebra: a general package for finitely generated, not-necessarily free R-modules; and multiplicative order for matrices over finite fields
- Miscellaneous: optimized Sudoku solver; a decorator for declaring abstract methods; and support Unicode in LaTeX cells (notebook)
- Number theory: improved random element generation for number field orders and ideals; support Michael Stoll's ratpoints package; and elliptic exponential
- Numerical: computing numerical values of constants using mpmath
- Update, upgrade 18 packages to latest upstream releases
Algebraic Geometry
Construct an elliptic curve from a plane curve of genus one (Lloyd Kilford, John Cremona ) -- New function EllipticCurve_from_plane_curve() in the module sage/schemes/elliptic_curves/constructor.py to allow the construction of an elliptic curve from a smooth plane cubic with a rational point. Currently, this function uses Magma and it will not work on machines that do not have Magma installed. Assuming you have Magma installed on your computer, we can use the function EllipticCurve_from_plane_curve() to first check that the Fermat cubic is isomorphic to the curve with Cremona label "27a1":
Here is a quartic example:sage: x, y, z = PolynomialRing(QQ, 3, 'xyz').gens() # optional - magma sage: C = Curve(x^3 + y^3 + z^3) # optional - magma sage: P = C(1, -1, 0) # optional - magma sage: E = EllipticCurve_from_plane_curve(C, P) # optional - magma sage: E # optional - magma Elliptic Curve defined by y^2 + y = x^3 - 7 over Rational Field sage: E.label() # optional - magma '27a1'
sage: u, v, w = PolynomialRing(QQ, 3, 'uvw').gens() # optional - magma sage: C = Curve(u^4 + u^2*v^2 - w^4) # optional - magma sage: P = C(1, 0, 1) # optional - magma sage: E = EllipticCurve_from_plane_curve(C, P) # optional - magma sage: E # optional - magma Elliptic Curve defined by y^2 = x^3 + 4*x over Rational Field sage: E.label() # optional - magma '32a1'
Basic Arithmetic
- Speed-up integer division (Robert Bradshaw ) -- In some cases, integer division is now up to 31% faster than previously. The following timing statistics were obtained using the machine sage.math:
# BEFORE sage: a = next_prime(2**31) sage: b = Integers(a)(100) sage: %timeit a % b; 1000000 loops, best of 3: 1.12 µs per loop sage: %timeit 101 // int(5); 1000000 loops, best of 3: 215 ns per loop sage: %timeit 100 // int(-3) 1000000 loops, best of 3: 214 ns per loop sage: a = ZZ.random_element(10**50) sage: b = ZZ.random_element(10**15) sage: %timeit a.quo_rem(b) 1000000 loops, best of 3: 454 ns per loop # AFTER sage: a = next_prime(2**31) sage: b = Integers(a)(100) sage: %timeit a % b; 1000000 loops, best of 3: 1.02 µs per loop sage: %timeit 101 // int(5); 1000000 loops, best of 3: 201 ns per loop sage: %timeit 100 // int(-3) 1000000 loops, best of 3: 194 ns per loop sage: a = ZZ.random_element(10**50) sage: b = ZZ.random_element(10**15) sage: %timeit a.quo_rem(b) 1000000 loops, best of 3: 313 ns per loop
Combinatorics
Irreducible matrix representations of symmetric groups (Franco Saliola) -- Support for constructing irreducible representations of the symmetric group. This is based on Alain Lascoux's article Young representations of the symmetric group. The following types of representations are supported:
- Specht representations -- The matrices have integer entries:
sage: chi = SymmetricGroupRepresentation([3, 2]); chi Specht representation of the symmetric group corresponding to [3, 2] sage: chi([5, 4, 3, 2, 1]) [ 1 -1 0 1 0] [ 0 0 -1 0 1] [ 0 0 0 -1 1] [ 0 1 -1 -1 1] [ 0 1 0 -1 1]
- Young's seminormal representation -- The matrices have rational entries:
sage: snorm = SymmetricGroupRepresentation([2, 1], "seminormal"); snorm Seminormal representation of the symmetric group corresponding to [2, 1] sage: snorm([1, 3, 2]) [-1/2 3/2] [ 1/2 1/2]
Young's orthogonal representation (the matrices are orthogonal) -- These matrices are defined over Sage's Symbolic Ring:
sage: ortho = SymmetricGroupRepresentation([3, 2], "orthogonal"); ortho Orthogonal representation of the symmetric group corresponding to [3, 2] sage: ortho([1, 3, 2, 4, 5]) [ 1 0 0 0 0] [ 0 -1/2 1/2*sqrt(3) 0 0] [ 0 1/2*sqrt(3) 1/2 0 0] [ 0 0 0 -1/2 1/2*sqrt(3)] [ 0 0 0 1/2*sqrt(3) 1/2]
You can also create the CombinatorialClass of all irreducible matrix representations of a given symmetric group. Then particular representations can be created by providing partitions. For example:
sage: chi = SymmetricGroupRepresentations(5); chi Specht representations of the symmetric group of order 5! over Integer Ring sage: chi([5]) # the trivial representation Specht representation of the symmetric group corresponding to [5] sage: chi([5])([2, 1, 3, 4, 5]) [1] sage: chi([1, 1, 1, 1, 1]) # the sign representation Specht representation of the symmetric group corresponding to [1, 1, 1, 1, 1] sage: chi([1, 1, 1, 1, 1])([2, 1, 3, 4, 5]) [-1] sage: chi([3, 2]) Specht representation of the symmetric group corresponding to [3, 2] sage: chi([3, 2])([5, 4, 3, 2, 1]) [ 1 -1 0 1 0] [ 0 0 -1 0 1] [ 0 0 0 -1 1] [ 0 1 -1 -1 1] [ 0 1 0 -1 1]
See the documentation of SymmetricGroupRepresentation and SymmetricGroupRepresentations for more information and examples.
- Specht representations -- The matrices have integer entries:
- Yang-Baxter graphs (Franco Saliola) -- Besides being used for constructing the irreducible matrix representations of the symmetric group, Yang-Baxter graphs can also be used to construct the Cayley graph of a finite group. For example:
sage: def left_multiplication_by(g): ....: return lambda h : h*g ....: sage: G = AlternatingGroup(4) sage: operators = [ left_multiplication_by(gen) for gen in G.gens() ] sage: Y = YangBaxterGraph(root=G.identity(), operators=operators); Y Yang-Baxter graph with root vertex () sage: Y.plot(edge_labels=False)
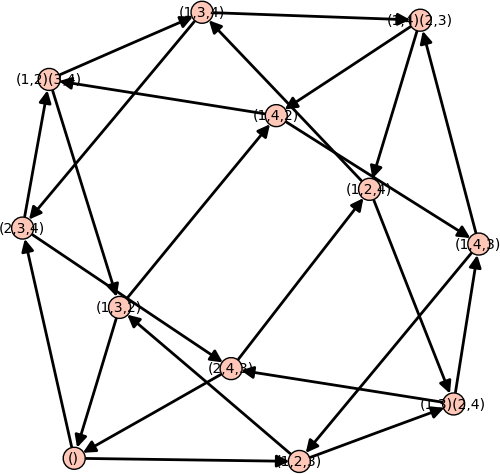
- Yang-Baxter graphs can also be used to construct the permutahedron:
sage: from sage.combinat.yang_baxter_graph import SwapIncreasingOperator sage: operators = [SwapIncreasingOperator(i) for i in range(3)] sage: Y = YangBaxterGraph(root=(1,2,3,4), operators=operators); Y Yang-Baxter graph with root vertex (1, 2, 3, 4) sage: Y.plot()
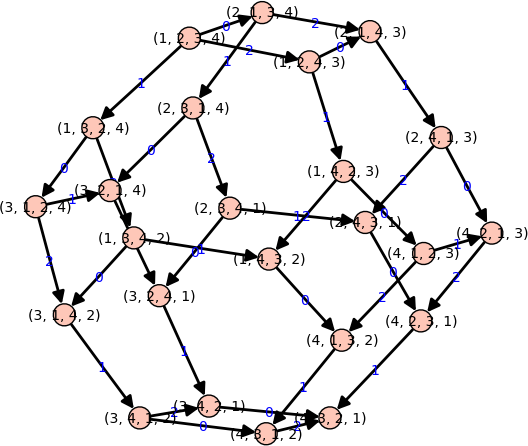
See the documentation of YangBaxterGraph for more information and examples.
Cryptography
Mini Advanced Encryption Standard for educational purposes (Minh Van Nguyen) -- New module sage/crypto/block_cipher/miniaes.py to support the Mini Advanced Encryption Standard (Mini-AES) to allow students to explore the working of a block cipher. This is a simplified variant of the Advanced Encryption Standard (AES) to be used for cryptography education. Mini-AES is described in the paper:
- A. C.-W. Phan. Mini advanced encryption standard (mini-AES): a testbed for cryptanalysis students. Cryptologia, 26(4):283--306, 2002.
Here is the decryption process:sage: from sage.crypto.block_cipher.miniaes import MiniAES sage: maes = MiniAES() sage: K = FiniteField(16, "x") sage: MS = MatrixSpace(K, 2, 2) sage: P = MS([K("x^3 + x"), K("x^2 + 1"), K("x^2 + x"), K("x^3 + x^2")]); P [ x^3 + x x^2 + 1] [ x^2 + x x^3 + x^2] sage: key = MS([K("x^3 + x^2"), K("x^3 + x"), K("x^3 + x^2 + x"), K("x^2 + x + 1")]); key [ x^3 + x^2 x^3 + x] [x^3 + x^2 + x x^2 + x + 1] sage: C = maes.encrypt(P, key); C [ x x^2 + x] [x^3 + x^2 + x x^3 + x]
We can also work directly with binary strings:sage: plaintxt = maes.decrypt(C, key) sage: plaintxt == P True
sage: from sage.crypto.block_cipher.miniaes import MiniAES sage: maes = MiniAES() sage: bin = BinaryStrings() sage: key = bin.encoding("KE"); key 0100101101000101 sage: P = bin.encoding("Encrypt this secret message!") sage: C = maes(P, key, algorithm="encrypt") sage: plaintxt = maes(C, key, algorithm="decrypt") sage: plaintxt == P True
Or work with integers n such that 0 <= n <= 15:
sage: from sage.crypto.block_cipher.miniaes import MiniAES sage: maes = MiniAES() sage: P = [n for n in xrange(16)]; P [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15] sage: key = [2, 3, 11, 0]; key [2, 3, 11, 0] sage: P = maes.integer_to_binary(P) sage: key = maes.integer_to_binary(key) sage: C = maes(P, key, algorithm="encrypt") sage: plaintxt = maes(C, key, algorithm="decrypt") sage: plaintxt == P True
Geometry
Graph Theory
- FIXME: summarize #6085
Improve accuracy of graph eigenvalues (Ticket #6258), Rob Beezer. New routines compute eigenvalues and eigenvectors of integer matrices more precisely than before. Rather than convert adjacency matrices of graphs to computations over the reals or complexes, this patch retains adjacency matrices as matrices over the integers, yielding more accurate and informative results for eigenvalues, eigenvectors, and eigenspaces.
- Examples follow for a circuit on 8 vertices:
g = graphs.CycleGraph(8) - Integer eigenvalues are exact, irrational eigenvalues are more precise, making multiplicities easier to determine.
sage: g.spectrum() [2, 1.414213562373095?, 1.414213562373095?, 0, 0, -1.414213562373095?, -1.414213562373095?, -2]
- Similar comments apply to eigenvectors.
sage: g.eigenvectors() [(2, [ (1, 1, 1, 1, 1, 1, 1, 1) ], 1), (-2, [ (1, -1, 1, -1, 1, -1, 1, -1) ], 1), (0, [ (1, 0, -1, 0, 1, 0, -1, 0), (0, 1, 0, -1, 0, 1, 0, -1) ], 2), (-1.414213562373095?, [(1, 0, -1, 1.414213562373095?, -1, 0, 1, -1.414213562373095?), (0, 1, -1.414213562373095?, 1, 0, -1, 1.414213562373095?, -1)], 2), (1.414213562373095?, [(1, 0, -1, -1.414213562373095?, -1, 0, 1, 1.414213562373095?), (0, 1, 1.414213562373095?, 1, 0, -1, -1.414213562373095?, -1)], 2)]
Eigenspaces are exact, in that they can be expressed as vector spaces over number fields. When the defining polynomial has several roots, the eigenspaces are not repeated. Previously eigenspaces were "fractured" owing to slight computational differences in identical eigenvalues. In concert with eigenvectors() this command illuminates the structure of a graph's eigenspaces more than purely numerical results.
sage: g.eigenspaces() [ (2, Vector space of degree 8 and dimension 1 over Rational Field User basis matrix: [1 1 1 1 1 1 1 1]), (-2, Vector space of degree 8 and dimension 1 over Rational Field User basis matrix: [ 1 -1 1 -1 1 -1 1 -1]), (0, Vector space of degree 8 and dimension 2 over Rational Field User basis matrix: [ 1 0 -1 0 1 0 -1 0] [ 0 1 0 -1 0 1 0 -1]), (a3, Vector space of degree 8 and dimension 2 over Number Field in a3 with defining polynomial x^2 - 2 User basis matrix: [ 1 0 -1 -a3 -1 0 1 a3] [ 0 1 a3 1 0 -1 -a3 -1])
- Complex eigenvalues (of digraphs) previously were missing their imaginary parts. This bug has been fixed as part of this ticket.
- Examples follow for a circuit on 8 vertices:
Graphics
- FIXME: summarize #6162
Group Theory
Interfaces
- FIXME: summarize #4313
Linear Algebra
- FIXME: summarize #6261
- FIXME: summarize #5882
Miscellaneous
- FIXME: summarize #3084
- FIXME: summarize #6097
- FIXME: summarize #6417
Modular Forms
Notebook
- FIXME: summarize #5637
Number Theory
- FIXME: summarize #6273
- FIXME: summarize #5854
- FIXME: summarize #6386
Numerical
- FIXME: summarize #6200
Packages
Upgrade Singular to version singular-3-1-0-2-20090620 with support for compiling with GCC 4.4.
- FIXME: summarize #6359
- FIXME: summarize #6196
- FIXME: summarize #6276
- FIXME: summarize #5517
- FIXME: summarize #5854
- FIXME: summarize #5866
- FIXME: summarize #5867
- FIXME: summarize #5868
- FIXME: summarize #5869
- FIXME: summarize #5870
- FIXME: summarize #5872
- FIXME: summarize #5874
- FIXME: summarize #5875
- FIXME: summarize #6281
- FIXME: summarize #6470
- FIXME: summarize #6470
- FIXME: summarize #6492
- FIXME: summarize #6408
P-adics
Quadratic Forms
Symbolics
- FIXME: summarize #6421
