|
Size: 1886
Comment: Reminders to showcase features
|
Size: 13235
Comment: Summarize #6298
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 11: | Line 11: |
| * FIXME: summarize #5845 * FIXME: summarize #6229 * FIXME: summarize #6250 |
* Correct precision bound in {{{hilbert_class_polynomial()}}} and miscellaneous new functions (John Cremona) -- The two new functions are {{{elliptic_j()}}} in {{{sage/functions/special.py}}}, and {{{is_primitive()}}} in the class {{{BinaryQF}}} of {{{sage/quadratic_forms/binary_qf.py}}}. The function {{{elliptic_j(z)}}} returns the elliptic modular {{{j}}}-function evaluated at {{{z}}}. The function {{{is_primitive()}}} determines whether the binary quadratic form {{{ax^2 + bxy + cy^2}}} satisfies {{{gcd(a,b,c) = 1}}}, i.e. that it is primitive. Here are some examples on using these new functions: {{{ sage: elliptic_j(CC(i)) 1728.00000000000 sage: elliptic_j(sqrt(-2.0)) 8000.00000000000 sage: Q = BinaryQF([6,3,9]) sage: Q.is_primitive() False sage: Q = BinaryQF([1,1,1]) sage: Q.is_primitive() True }}} * Efficient Lagrange interpolation polynomial (Yann Laigle-Chapuy) -- Calculating the Lagrange interpolation polynomial of a set of points is now up to 48% faster than previously. The following timing statistics were obtained using the machine sage.math: {{{ # BEFORE sage: R = PolynomialRing(QQ, 'x') sage: %timeit R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) 1000 loops, best of 3: 824 µs per loop sage: R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) -23/84*x^3 - 11/84*x^2 + 13/7*x + 1 sage: R = PolynomialRing(GF(2**3,'a'), 'x') sage: a = R.base_ring().gen() sage: timeit("R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)])") 625 loops, best of 3: 111 µs per loop sage: R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)]) a^2*x^2 + a^2*x + a^2 # AFTER sage: R = PolynomialRing(QQ, 'x') sage: %timeit R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) 1000 loops, best of 3: 425 µs per loop sage: R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) -23/84*x^3 - 11/84*x^2 + 13/7*x + 1 sage: R = PolynomialRing(GF(2**3,'a'), 'x') sage: a = R.base_ring().gen() sage: timeit("R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)])") 625 loops, best of 3: 86.4 µs per loop sage: R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)]) a^2*x^2 + a^2*x + a^2 }}} * Deprecate the method {{{__len__()}}} for a matrix group (Nicolas Thiery) -- The method {{{__len__()}}} of the class {{{MatrixGroup_gap}}} in {{{sage/groups/matrix_gps/matrix_group.py}}} is now deprecated and will be removed in a future release. To get the number of elements in a matrix group, users are advised to use the method {{{cardinality()}}} instead. The method {{{order()}}} is essentially the same as {{{cardinality()}}}, so {{{order()}}} will be deprecated in a future release. |
| Line 21: | Line 65: |
| * FIXME: summarize #6218 == Basic Arithmetic == == Build == * FIXME: summarize #6234 == Calculus == |
* Optimize hyperelliptic curve arithmetic (Nick Alexander) -- Arithmetics with hyperelliptic curves can be up to 6x faster than previously. The following timing statistics were obtained using the maching sage.math: {{{ #BEFORE sage: F = GF(next_prime(10^30)) sage: x = F['x'].gen() sage: f = x^7 + x^2 + 1 sage: H = HyperellipticCurve(f, 2*x) sage: J = H.jacobian()(F) verbose 0 (902: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation. sage: Q = J(H.lift_x(F(1))) sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.65 s, sys: 0.02 s, total: 0.67 s Wall time: 0.68 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 1.08 s, sys: 0.00 s, total: 1.08 s Wall time: 1.08 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.72 s, sys: 0.02 s, total: 0.74 s Wall time: 0.74 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.67 s, sys: 0.00 s, total: 0.67 s Wall time: 0.67 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.66 s, sys: 0.00 s, total: 0.66 s Wall time: 0.66 s # AFTER sage: F = GF(next_prime(10^30)) sage: x = F['x'].gen() sage: f = x^7 + x^2 + 1 sage: H = HyperellipticCurve(f, 2*x) sage: J = H.jacobian()(F) verbose 0 (919: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation. sage: Q = J(H.lift_x(F(1))) sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.14 s, sys: 0.01 s, total: 0.15 s Wall time: 0.15 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.10 s, sys: 0.00 s, total: 0.10 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.09 s, sys: 0.00 s, total: 0.09 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.09 s, sys: 0.01 s, total: 0.10 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.10 s, sys: 0.00 s, total: 0.10 s Wall time: 0.11 s }}} |
| Line 39: | Line 123: |
| * FIXME: summarize #6014 == Combinatorics == |
* Hexads in {{{S(5,6,12)}}} and mathematical blackjack (David Joyner) -- Implements kittens, hexads and mathematical blackjack as described in the following papers: * R. Curtis. The Steiner system {{{S(5,6,12)}}}, the Mathieu group {{{M_{12}}}}, and the kitten. In M. Atkinson (ed.) Computational Group Theory, Academic Press, 1984. * J. Conway. Hexacode and tetracode -- MINIMOG and MOG. In M. Atkinson (ed.) Computational Group Theory, Academic Press, 1984. * J. Conway and N. Sloane. Lexicographic codes: error-correcting codes from game theory. IEEE Transactions on Information Theory, 32:337-348, 1986. * J. Kahane and A. Ryba. The hexad game. Electronic Journal of Combinatorics, 8, 2001. http://www.combinatorics.org/Volume_8/Abstracts/v8i2r11.html |
| Line 48: | Line 133: |
| * FIXME: summarize #6051 | * Enable Singular's coefficient rings which are not fields (Martin Albrecht) -- Singular 3-1-0 supports coefficient rings which are not fields. In particular, it supports {{{ZZ}}} and {{{ZZ/nZZ}}} now. These are now natively supported in Sage. |
| Line 54: | Line 139: |
| * FIXME: summarize #6185 | * S-box to CNF Conversion (Martin Albrecht) -- New method {{{cnf()}}} in the class {{{SBox}}} of {{{sage/crypto/mq/sbox.py}}} for converting an S-box to conjunctive normal form. Here are some examples on S-box to CNF conversion: {{{ sage: S = mq.SBox(1,2,0,3); S (1, 2, 0, 3) sage: S.cnf() [(1, 2, -3), (1, 2, 4), (1, -2, 3), (1, -2, -4), (-1, 2, -3), (-1, 2, -4), (-1, -2, 3), (-1, -2, 4)] sage: # convert this representation to the DIMACS format sage: print S.cnf(format='dimacs') p cnf 4 8 1 2 -3 0 1 2 4 0 1 -2 3 0 1 -2 -4 0 -1 2 -3 0 -1 2 -4 0 -1 -2 3 0 -1 -2 4 0 sage: # as a truth table sage: log = SymbolicLogic() sage: s = log.statement(S.cnf(format='symbolic')) sage: log.truthtable(s)[1:] [['False', 'False', 'False', 'False', 'False'], ['False', 'False', 'False', 'True', 'False'], ['False', 'False', 'True', 'False', 'False'], ['False', 'False', 'True', 'True', 'True'], ['False', 'True', 'False', 'False', 'True'], ['False', 'True', 'False', 'True', 'True'], ['False', 'True', 'True', 'False', 'True'], ['False', 'True', 'True', 'True', 'True'], ['True', 'False', 'False', 'False', 'True'], ['True', 'False', 'False', 'True', 'True'], ['True', 'False', 'True', 'False', 'True'], ['True', 'False', 'True', 'True', 'True'], ['True', 'True', 'False', 'False', 'True'], ['True', 'True', 'False', 'True', 'True'], ['True', 'True', 'True', 'False', 'True'], ['True', 'True', 'True', 'True', 'True']] }}} |
| Line 60: | Line 192: |
| * FIXME: summarize #5975 == Graphics == |
* LaTeX output for (combinatorial) graphs (Robert Beezer, Fidel Barrera Cruz) -- Implement the option {{{tkz_style}}} to output graphs in LaTeX format so that they could be processed by pgf/tkz. Here's an example of the Petersen graph visualized using tkz: {{{ g = graphs.PetersenGraph() g.set_latex_options(tkz_style='Art') view(g, pdflatex=True) }}} {{attachment:petersen-latex.png}} |
| Line 69: | Line 204: |
| * FIXME: summarize #6263 == Interfaces == |
* Python interface to partition backtrack functions (Robert Miller) -- New module in {{{sage/groups/perm_gps/partn_ref/refinement_python.pyx}}} provides Python frontends to the Cython-based partition backtrack functions. This allows one to write the three input functions ({{{all_children_are_equivalent}}}, {{{refine_and_return_invariant}}}, and {{{compare_structures}}}) in pure Python, and still use the Cython algorithms. Experimentation with specific partition backtrack implementations no longer requires compilation, as the input functions can be dynamically changed at runtime. Note that this is not intended for production quality implementations of partition refinement, but instead for experimentation, learning, and use of the Python debugger. |
| Line 78: | Line 210: |
| * FIXME: summarize #6178 * FIXME: summarize #5510 |
* Hermite normal form over principal ideal domains (David Loeffler) -- This adds echelon form (or Hermite normal form) over principal ideal domains. Here an example: {{{ sage: L.<w> = NumberField(x^2 - x + 2) sage: OL = L.ring_of_integers() sage: m = matrix(OL, 2, 2, [1,2,3,4+w]) sage: m.echelon_form() [ 1 -2] [ 0 w - 2] sage: m.echelon_form(transformation=True) ([ 1 -2] [ 0 w - 2], [-3*w - 2 w + 1] [ -3 1]) }}} |
| Line 86: | Line 228: |
| * FIXME: summarize #6089 * FIXME: summarize #6110 == Modular Forms == |
* Bypassing jsMath with view command (John Palmieri) -- This provides a way to not always use jsMath when rendering LaTeX for the {{{view}}} command in the notebook. It works by looking for certain strings in the LaTeX code for the object, and if it finds them, it creates and displays a PNG file, bypassing jsMath altogether. The "certain strings" are stored in a list which is initially empty, but can be populated by using {{{ latex.jsmath_avoid_list(...) }}} or {{{ latex.add_to_jsmath_avoid_list(...) }}} * A "decorator" to allow pickling nested classes (Carl Witty, Nicolas Thiery) -- The {{{nested_pickle}}} decorator modifies nested classes to be picklable. (In Python 2.6 it should be usable as a decorator, although that hasn't been tested; Python 2.5 doesn't support class decorators, so you can't use that syntax in Sage until Sage upgrades to Python 2.6.) |
| Line 97: | Line 244: |
| * FIXME: summarize #6259 * FIXME: summarize #6225 * FIXME: summarize #5371 |
* Add link to IRC in notebook help page (Harald Schilly). |
| Line 107: | Line 250: |
| * FIXME: summarize #5976 * FIXME: summarize #5842 * FIXME: summarize #6205 * FIXME: summarize #6193 * FIXME: summarize #6044 == Numerical == |
* Elliptic curve isogeny object (Dan Shumow). * Various number field improvements (Francis Clarke) -- Among other things, one can now do {{{ sage: K.<a> = NumberField(x^2 + 5) sage: L.<b> = K.extension(x^2 + 1) sage: L.ideal(K.ideal(2, a + 1)) Fractional ideal (b + 1) }}} For a number field {{{K}}}, one can obtain the prime factors using {{{K.prime_factors}}}: {{{ sage: CyclotomicField(3).prime_factors(7) [Fractional ideal (-2*zeta3 + 1), Fractional ideal (2*zeta3 + 3)] }}} * Enhanced reduction modulo ideals of number fields (Maite Aranes) -- The function {{{residues()}}} is modified so that it returns a canonical set of coset representatives. The new function {{{reduce()}}} returns the canonical reduction of an integral element of a number field modulo self. The function {{{inverse_mod}}} now works for integral elements of a number field without having to coerce to the ring of integers. * Local and global heights for number field elements (John Cremona) -- New method {{{local_height()}}} and {{{global_height()}}} in the class {{{NumberFieldElement}}} of {{{sage/rings/number_field/number_field_element.pyx}}}. The method {{{local_height()}}} returns the local height of a number field element at a given prime ideal. The method {{{global_height()}}} returns the absolute logarithmic height of a number field element. Here are some examples for working with these new methods: {{{ sage: R.<x> = QQ["x"] sage: K.<a> = NumberField(x^4 + 3*x^2 - 17) sage: P = K.ideal(61).factor()[0][0] sage: b = 1/(a^2 + 30) sage: b.local_height(P) 4.11087386417331 sage: b.local_height(P, weighted=True) 8.22174772834662 sage: b.local_height(P, 200) 4.1108738641733112487513891034256147463156817430812610629374 sage: (b^2).local_height(P) 8.22174772834662 sage: (b^-1).local_height(P) 0.000000000000000 sage: sage: R.<x> = QQ["x"] sage: K.<a> = NumberField(x^4 + 3*x^2 - 17) sage: b = a/2 sage: b.global_height() 2.86922224068797 sage: b.global_height(prec=200) 2.8692222406879748488543678846959454765968722137813736080066 }}} |
| Line 133: | Line 309: |
| * Upgrade [[http://www.flintlib.org|FLINT]] to version 1.3.0 latest upstream release (Nick Alexander). * Update the [[http://www.mpir.org|MPIR]] spkg to version {{{mpir-1.2.p3.spkg}}} (Nick Alexander). * Update the [[http://m4ri.sagemath.org|M4RI]] spkg to version {{{libm4ri-20090617}}} (Martin Albrecht). |
|
| Line 136: | Line 321: |
| == Symbolics == == Topology == |
* New experimental spkg {{{libcocoa-0.9930.spkg}}} (William Stein). |
Sage 4.0.2 Release Tour
Sage 4.0.2 was released on FIXME. For the official, comprehensive release note, please refer to FIXME. A nicely formatted version of this release tour can be found at FIXME. The following points are some of the foci of this release:
Algebra
Correct precision bound in hilbert_class_polynomial() and miscellaneous new functions (John Cremona) -- The two new functions are elliptic_j() in sage/functions/special.py, and is_primitive() in the class BinaryQF of sage/quadratic_forms/binary_qf.py. The function elliptic_j(z) returns the elliptic modular j-function evaluated at z. The function is_primitive() determines whether the binary quadratic form ax^2 + bxy + cy^2 satisfies gcd(a,b,c) = 1, i.e. that it is primitive. Here are some examples on using these new functions:
sage: elliptic_j(CC(i)) 1728.00000000000 sage: elliptic_j(sqrt(-2.0)) 8000.00000000000 sage: Q = BinaryQF([6,3,9]) sage: Q.is_primitive() False sage: Q = BinaryQF([1,1,1]) sage: Q.is_primitive() True
- Efficient Lagrange interpolation polynomial (Yann Laigle-Chapuy) -- Calculating the Lagrange interpolation polynomial of a set of points is now up to 48% faster than previously. The following timing statistics were obtained using the machine sage.math:
# BEFORE sage: R = PolynomialRing(QQ, 'x') sage: %timeit R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) 1000 loops, best of 3: 824 µs per loop sage: R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) -23/84*x^3 - 11/84*x^2 + 13/7*x + 1 sage: R = PolynomialRing(GF(2**3,'a'), 'x') sage: a = R.base_ring().gen() sage: timeit("R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)])") 625 loops, best of 3: 111 µs per loop sage: R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)]) a^2*x^2 + a^2*x + a^2 # AFTER sage: R = PolynomialRing(QQ, 'x') sage: %timeit R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) 1000 loops, best of 3: 425 µs per loop sage: R.lagrange_polynomial([(0,1),(2,2),(3,-2),(-4,9)]) -23/84*x^3 - 11/84*x^2 + 13/7*x + 1 sage: R = PolynomialRing(GF(2**3,'a'), 'x') sage: a = R.base_ring().gen() sage: timeit("R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)])") 625 loops, best of 3: 86.4 µs per loop sage: R.lagrange_polynomial([(a^2+a,a),(a,1),(a^2,a^2+a+1)]) a^2*x^2 + a^2*x + a^2 Deprecate the method __len__() for a matrix group (Nicolas Thiery) -- The method __len__() of the class MatrixGroup_gap in sage/groups/matrix_gps/matrix_group.py is now deprecated and will be removed in a future release. To get the number of elements in a matrix group, users are advised to use the method cardinality() instead. The method order() is essentially the same as cardinality(), so order() will be deprecated in a future release.
Algebraic Geometry
- Optimize hyperelliptic curve arithmetic (Nick Alexander) -- Arithmetics with hyperelliptic curves can be up to 6x faster than previously. The following timing statistics were obtained using the maching sage.math:
#BEFORE sage: F = GF(next_prime(10^30)) sage: x = F['x'].gen() sage: f = x^7 + x^2 + 1 sage: H = HyperellipticCurve(f, 2*x) sage: J = H.jacobian()(F) verbose 0 (902: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation. sage: Q = J(H.lift_x(F(1))) sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.65 s, sys: 0.02 s, total: 0.67 s Wall time: 0.68 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 1.08 s, sys: 0.00 s, total: 1.08 s Wall time: 1.08 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.72 s, sys: 0.02 s, total: 0.74 s Wall time: 0.74 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.67 s, sys: 0.00 s, total: 0.67 s Wall time: 0.67 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.66 s, sys: 0.00 s, total: 0.66 s Wall time: 0.66 s # AFTER sage: F = GF(next_prime(10^30)) sage: x = F['x'].gen() sage: f = x^7 + x^2 + 1 sage: H = HyperellipticCurve(f, 2*x) sage: J = H.jacobian()(F) verbose 0 (919: multi_polynomial_ideal.py, dimension) Warning: falling back to very slow toy implementation. sage: Q = J(H.lift_x(F(1))) sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.14 s, sys: 0.01 s, total: 0.15 s Wall time: 0.15 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.10 s, sys: 0.00 s, total: 0.10 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.09 s, sys: 0.00 s, total: 0.09 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.09 s, sys: 0.01 s, total: 0.10 s Wall time: 0.10 s sage: %time ZZ.random_element(10**10) * Q; CPU times: user 0.10 s, sys: 0.00 s, total: 0.10 s Wall time: 0.11 s
Coding Theory
Hexads in S(5,6,12) and mathematical blackjack (David Joyner) -- Implements kittens, hexads and mathematical blackjack as described in the following papers:
R. Curtis. The Steiner system S(5,6,12), the Mathieu group M_{12}, and the kitten. In M. Atkinson (ed.) Computational Group Theory, Academic Press, 1984.
- J. Conway. Hexacode and tetracode -- MINIMOG and MOG. In M. Atkinson (ed.) Computational Group Theory, Academic Press, 1984.
- J. Conway and N. Sloane. Lexicographic codes: error-correcting codes from game theory. IEEE Transactions on Information Theory, 32:337-348, 1986.
J. Kahane and A. Ryba. The hexad game. Electronic Journal of Combinatorics, 8, 2001. http://www.combinatorics.org/Volume_8/Abstracts/v8i2r11.html
Commutative Algebra
Enable Singular's coefficient rings which are not fields (Martin Albrecht) -- Singular 3-1-0 supports coefficient rings which are not fields. In particular, it supports ZZ and ZZ/nZZ now. These are now natively supported in Sage.
Cryptography
S-box to CNF Conversion (Martin Albrecht) -- New method cnf() in the class SBox of sage/crypto/mq/sbox.py for converting an S-box to conjunctive normal form. Here are some examples on S-box to CNF conversion:
sage: S = mq.SBox(1,2,0,3); S (1, 2, 0, 3) sage: S.cnf() [(1, 2, -3), (1, 2, 4), (1, -2, 3), (1, -2, -4), (-1, 2, -3), (-1, 2, -4), (-1, -2, 3), (-1, -2, 4)] sage: # convert this representation to the DIMACS format sage: print S.cnf(format='dimacs') p cnf 4 8 1 2 -3 0 1 2 4 0 1 -2 3 0 1 -2 -4 0 -1 2 -3 0 -1 2 -4 0 -1 -2 3 0 -1 -2 4 0 sage: # as a truth table sage: log = SymbolicLogic() sage: s = log.statement(S.cnf(format='symbolic')) sage: log.truthtable(s)[1:] [['False', 'False', 'False', 'False', 'False'], ['False', 'False', 'False', 'True', 'False'], ['False', 'False', 'True', 'False', 'False'], ['False', 'False', 'True', 'True', 'True'], ['False', 'True', 'False', 'False', 'True'], ['False', 'True', 'False', 'True', 'True'], ['False', 'True', 'True', 'False', 'True'], ['False', 'True', 'True', 'True', 'True'], ['True', 'False', 'False', 'False', 'True'], ['True', 'False', 'False', 'True', 'True'], ['True', 'False', 'True', 'False', 'True'], ['True', 'False', 'True', 'True', 'True'], ['True', 'True', 'False', 'False', 'True'], ['True', 'True', 'False', 'True', 'True'], ['True', 'True', 'True', 'False', 'True'], ['True', 'True', 'True', 'True', 'True']]
Graph Theory
LaTeX output for (combinatorial) graphs (Robert Beezer, Fidel Barrera Cruz) -- Implement the option tkz_style to output graphs in LaTeX format so that they could be processed by pgf/tkz. Here's an example of the Petersen graph visualized using tkz:
g = graphs.PetersenGraph() g.set_latex_options(tkz_style='Art') view(g, pdflatex=True)
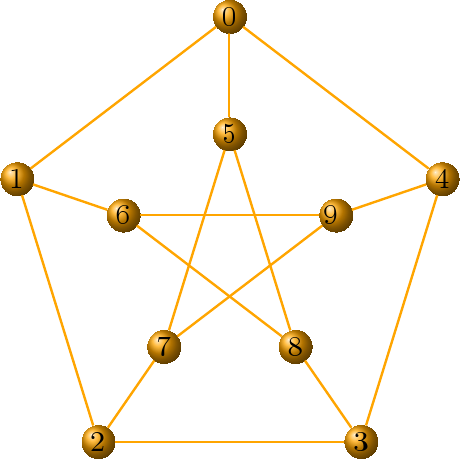
Group Theory
Python interface to partition backtrack functions (Robert Miller) -- New module in sage/groups/perm_gps/partn_ref/refinement_python.pyx provides Python frontends to the Cython-based partition backtrack functions. This allows one to write the three input functions (all_children_are_equivalent, refine_and_return_invariant, and compare_structures) in pure Python, and still use the Cython algorithms. Experimentation with specific partition backtrack implementations no longer requires compilation, as the input functions can be dynamically changed at runtime. Note that this is not intended for production quality implementations of partition refinement, but instead for experimentation, learning, and use of the Python debugger.
Linear Algebra
- Hermite normal form over principal ideal domains (David Loeffler) -- This adds echelon form (or Hermite normal form) over principal ideal domains. Here an example:
sage: L.<w> = NumberField(x^2 - x + 2) sage: OL = L.ring_of_integers() sage: m = matrix(OL, 2, 2, [1,2,3,4+w]) sage: m.echelon_form() [ 1 -2] [ 0 w - 2] sage: m.echelon_form(transformation=True) ([ 1 -2] [ 0 w - 2], [-3*w - 2 w + 1] [ -3 1])
Miscellaneous
Bypassing jsMath with view command (John Palmieri) -- This provides a way to not always use jsMath when rendering LaTeX for the view command in the notebook. It works by looking for certain strings in the LaTeX code for the object, and if it finds them, it creates and displays a PNG file, bypassing jsMath altogether. The "certain strings" are stored in a list which is initially empty, but can be populated by using
latex.jsmath_avoid_list(...)
orlatex.add_to_jsmath_avoid_list(...)
A "decorator" to allow pickling nested classes (Carl Witty, Nicolas Thiery) -- The nested_pickle decorator modifies nested classes to be picklable. (In Python 2.6 it should be usable as a decorator, although that hasn't been tested; Python 2.5 doesn't support class decorators, so you can't use that syntax in Sage until Sage upgrades to Python 2.6.)
Notebook
- Add link to IRC in notebook help page (Harald Schilly).
Number Theory
- Elliptic curve isogeny object (Dan Shumow).
- Various number field improvements (Francis Clarke) -- Among other things, one can now do
sage: K.<a> = NumberField(x^2 + 5) sage: L.<b> = K.extension(x^2 + 1) sage: L.ideal(K.ideal(2, a + 1)) Fractional ideal (b + 1)
For a number field K, one can obtain the prime factors using K.prime_factors:
sage: CyclotomicField(3).prime_factors(7) [Fractional ideal (-2*zeta3 + 1), Fractional ideal (2*zeta3 + 3)]
Enhanced reduction modulo ideals of number fields (Maite Aranes) -- The function residues() is modified so that it returns a canonical set of coset representatives. The new function reduce() returns the canonical reduction of an integral element of a number field modulo self. The function inverse_mod now works for integral elements of a number field without having to coerce to the ring of integers.
Local and global heights for number field elements (John Cremona) -- New method local_height() and global_height() in the class NumberFieldElement of sage/rings/number_field/number_field_element.pyx. The method local_height() returns the local height of a number field element at a given prime ideal. The method global_height() returns the absolute logarithmic height of a number field element. Here are some examples for working with these new methods:
sage: R.<x> = QQ["x"] sage: K.<a> = NumberField(x^4 + 3*x^2 - 17) sage: P = K.ideal(61).factor()[0][0] sage: b = 1/(a^2 + 30) sage: b.local_height(P) 4.11087386417331 sage: b.local_height(P, weighted=True) 8.22174772834662 sage: b.local_height(P, 200) 4.1108738641733112487513891034256147463156817430812610629374 sage: (b^2).local_height(P) 8.22174772834662 sage: (b^-1).local_height(P) 0.000000000000000 sage: sage: R.<x> = QQ["x"] sage: K.<a> = NumberField(x^4 + 3*x^2 - 17) sage: b = a/2 sage: b.global_height() 2.86922224068797 sage: b.global_height(prec=200) 2.8692222406879748488543678846959454765968722137813736080066
Packages
Upgrade NumPy to version 1.3.0 latest upstream release (Jason Grout).
Upgrade SciPy to version 0.7 latest upstream release (Jason Grout).
Upgrade Singular to version 3-1-0 latest upstream release (Martin Albrecht).
Upgrade FLINT to version 1.3.0 latest upstream release (Nick Alexander).
Update the MPIR spkg to version mpir-1.2.p3.spkg (Nick Alexander).
Update the M4RI spkg to version libm4ri-20090617 (Martin Albrecht).
Remove Guava as a standard Sage package (David Joyner).
New experimental spkg libcocoa-0.9930.spkg (William Stein).
