|
Size: 987
Comment: Lay out general structure of release tour for Sage 3.4.2
|
Size: 5842
Comment: Summarize #5928, #5914
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 11: | Line 11: |
| * FIXME: summarize #5820 * FIXME: summarize #5921 * Coercing factors into a common universe (Alex Ghitza) -- New method {{{base_change(self, U)}}} in the module {{{sage/structure/factorization.py}}} to allow the factorization {{{self}}} with its factors (including the unit part) coerced into the universe {{{U}}}. Here's an example for working with the new method {{{base_change()}}}: {{{ sage: F = factor(2006) sage: F.universe() Integer Ring sage: P.<x> = ZZ["x"] sage: F.base_change(P).universe() Univariate Polynomial Ring in x over Integer Ring }}} |
|
| Line 17: | Line 33: |
| * Enhancements to symbolic logic (Chris Gorecki) -- This adds a number of utilities for working with symbolic logic: 1. {{{sage/logic/booleval.py}}} -- For evaluating boolean formulas. 1. {{{sage/logic/boolformula.py}}} -- For boolean evaluation of boolean formulas. 1. {{{sage/logic/logicparser.py}}} -- For creating and modifying parse trees of well-formed boolean formulas. 1. {{{sage/logic/logictable.py}}} -- For creating and printing truth tables associated with logical statements. 1. {{{sage/logic/propcalc.py}}} -- For propositional calculus. Here are some examples for working with the new symbolic logic modules: {{{ sage: import sage.logic.propcalc as propcalc sage: f = propcalc.formula("a&((b|c)^a->c)<->b") sage: g = propcalc.formula("boolean<->algebra") sage: (f&~g).ifthen(f) ((a&((b|c)^a->c)<->b)&(~(boolean<->algebra)))->(a&((b|c)^a->c)<->b) sage: f.truthtable() a b c value False False False True False False True True False True False False False True True False True False False True True False True False True True False True True True True True }}} * New function {{{squarefree_divisors()}}} (Robert Miller) -- The new function {{{squarefree_divisors(x)}}} in the module {{{sage/rings/arith.py}}} allows for iterating over the squarefree divisors (up to units) of the element {{{x}}}. Here, we assume that {{{x}}} is an element of any ring for which the function {{{prime_divisors()}}} works. Below are some examples for working with the new function {{{squarefree_divisors()}}}: {{{ sage: list(squarefree_divisors(7)) [1, 7] sage: list(squarefree_divisors(6)) [1, 2, 3, 6] sage: list(squarefree_divisors(81)) [1, 3] }}} |
|
| Line 29: | Line 83: |
| * Make {{{cartan_type}}} a method rather than an attribute (Dan Bump) -- For the module {{{sage/combinat/root_system/weyl_characters.py}}}, {{{cartan_type}}} is now a method, not an attribute. For example, one can now invoke {{{cartan_type}}} as a method like so: {{{ sage: A2 = WeylCharacterRing("A2") sage: A2([1,0,0]).cartan_type() ['A', 2] }}} |
|
| Line 32: | Line 94: |
| * Improved performance in {{{MPolynomialRing_libsingular}}} (Simon King) -- This provides some optimization of the method {{{MPolynomialRing_libsingular.__call__()}}}. In some cases, the efficiency is up to 19%. The following timing statistics are obtained using the machine sage.math: {{{ # BEFORE sage: R = PolynomialRing(QQ,5,"x") sage: S = PolynomialRing(QQ,6,"x") sage: T = PolynomialRing(QQ,5,"y") sage: U = PolynomialRing(GF(2),5,"x") sage: p = R("x0*x1+2*x4+x3*x1^2")^4 sage: timeit("q = S(p)") 625 loops, best of 3: 321 µs per loop sage: timeit("q = T(p)") 625 loops, best of 3: 348 µs per loop sage: timeit("q = U(p)") 625 loops, best of 3: 435 µs per loop # AFTER sage: R = PolynomialRing(QQ,5,"x") sage: S = PolynomialRing(QQ,6,"x") sage: T = PolynomialRing(QQ,5,"y") sage: U = PolynomialRing(GF(2),5,"x") sage: p = R("x0*x1+2*x4+x3*x1^2")^4 sage: timeit("q = S(p)") 625 loops, best of 3: 316 µs per loop sage: timeit("q = T(p)") 625 loops, best of 3: 281 µs per loop sage: timeit("q = U(p)") 625 loops, best of 3: 392 µs per loop }}} |
|
| Line 41: | Line 136: |
| * FIXME: summarize #5610 |
|
| Line 47: | Line 145: |
| * Default edge color is black (Robert Miller) -- If only one edge of a graph is colored red, for example, then the remaining edges should be colored with black by default. Here's an example: {{{ sage: G = graphs.CompleteGraph(5) sage: G.show(edge_colors={'red':[(0,1)]}) }}} {{attachment:pentagon-graph.png}} |
|
| Line 56: | Line 162: |
| * FIXME: summarize #5111 |
|
| Line 59: | Line 168: |
| * FIXME: summarize #5886 |
|
| Line 65: | Line 177: |
| * FIXME: summarize #5876 |
|
| Line 68: | Line 183: |
| * FIXME: summarize #5912 * FIXME: summarize #2740 * FIXME: summarize #5880 |
|
| Line 71: | Line 193: |
| * FIXME: summarize #5130 * FIXME: summarize #5822 * FIXME: summarize #5704 * FIXME: summarize #4193 * FIXME: summarize #5890 * FIXME: summarize #5856 |
|
| Line 77: | Line 212: |
| * FIXME: summarize #5803 * FIXME: summarize #5849 * Move DSage to its own spkg (William Stein) -- The Distributed Sage framework (DSage) contained in {{{sage/dsage}}} is now packaged as a self-contained spkg. DSage allows for distributed computing from within Sage. == P-adics == * FIXME: summarize #5946 |
Sage 3.4.2 Release Tour
Sage 3.4.2 was released on FIXME. For the official, comprehensive release note, please refer to sage-3.4.2.txt. A nicely formatted version of this release tour can be found at FIXME. The following points are some of the foci of this release:
Algebra
- FIXME: summarize #5820
- FIXME: summarize #5921
Coercing factors into a common universe (Alex Ghitza) -- New method base_change(self, U) in the module sage/structure/factorization.py to allow the factorization self with its factors (including the unit part) coerced into the universe U. Here's an example for working with the new method base_change():
sage: F = factor(2006) sage: F.universe() Integer Ring sage: P.<x> = ZZ["x"] sage: F.base_change(P).universe() Univariate Polynomial Ring in x over Integer Ring
Algebraic Geometry
Basic Arithmetic
- Enhancements to symbolic logic (Chris Gorecki) -- This adds a number of utilities for working with symbolic logic:
sage/logic/booleval.py -- For evaluating boolean formulas.
sage/logic/boolformula.py -- For boolean evaluation of boolean formulas.
sage/logic/logicparser.py -- For creating and modifying parse trees of well-formed boolean formulas.
sage/logic/logictable.py -- For creating and printing truth tables associated with logical statements.
sage/logic/propcalc.py -- For propositional calculus.
sage: import sage.logic.propcalc as propcalc sage: f = propcalc.formula("a&((b|c)^a->c)<->b") sage: g = propcalc.formula("boolean<->algebra") sage: (f&~g).ifthen(f) ((a&((b|c)^a->c)<->b)&(~(boolean<->algebra)))->(a&((b|c)^a->c)<->b) sage: f.truthtable() a b c value False False False True False False True True False True False False False True True False True False False True True False True False True True False True True True True True New function squarefree_divisors() (Robert Miller) -- The new function squarefree_divisors(x) in the module sage/rings/arith.py allows for iterating over the squarefree divisors (up to units) of the element x. Here, we assume that x is an element of any ring for which the function prime_divisors() works. Below are some examples for working with the new function squarefree_divisors():
sage: list(squarefree_divisors(7)) [1, 7] sage: list(squarefree_divisors(6)) [1, 2, 3, 6] sage: list(squarefree_divisors(81)) [1, 3]
Build
Calculus
Coercion
Combinatorics
Make cartan_type a method rather than an attribute (Dan Bump) -- For the module sage/combinat/root_system/weyl_characters.py, cartan_type is now a method, not an attribute. For example, one can now invoke cartan_type as a method like so:
sage: A2 = WeylCharacterRing("A2") sage: A2([1,0,0]).cartan_type() ['A', 2]
Commutative Algebra
Improved performance in MPolynomialRing_libsingular (Simon King) -- This provides some optimization of the method MPolynomialRing_libsingular.__call__(). In some cases, the efficiency is up to 19%. The following timing statistics are obtained using the machine sage.math:
# BEFORE sage: R = PolynomialRing(QQ,5,"x") sage: S = PolynomialRing(QQ,6,"x") sage: T = PolynomialRing(QQ,5,"y") sage: U = PolynomialRing(GF(2),5,"x") sage: p = R("x0*x1+2*x4+x3*x1^2")^4 sage: timeit("q = S(p)") 625 loops, best of 3: 321 µs per loop sage: timeit("q = T(p)") 625 loops, best of 3: 348 µs per loop sage: timeit("q = U(p)") 625 loops, best of 3: 435 µs per loop # AFTER sage: R = PolynomialRing(QQ,5,"x") sage: S = PolynomialRing(QQ,6,"x") sage: T = PolynomialRing(QQ,5,"y") sage: U = PolynomialRing(GF(2),5,"x") sage: p = R("x0*x1+2*x4+x3*x1^2")^4 sage: timeit("q = S(p)") 625 loops, best of 3: 316 µs per loop sage: timeit("q = T(p)") 625 loops, best of 3: 281 µs per loop sage: timeit("q = U(p)") 625 loops, best of 3: 392 µs per loop
Distribution
Doctest
Documentation
- FIXME: summarize #5610
Geometry
Graph Theory
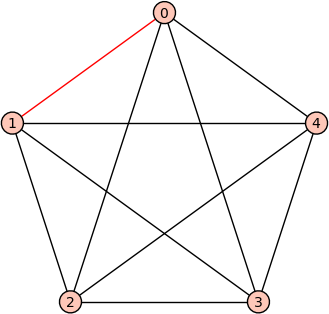
- Default edge color is black (Robert Miller) -- If only one edge of a graph is colored red, for example, then the remaining edges should be colored with black by default. Here's an example:
sage: G = graphs.CompleteGraph(5) sage: G.show(edge_colors={'red':[(0,1)]})
Graphics
Group Theory
Interfaces
- FIXME: summarize #5111
Linear Algebra
- FIXME: summarize #5886
Miscellaneous
Modular Forms
- FIXME: summarize #5876
Notebook
- FIXME: summarize #5912
- FIXME: summarize #2740
- FIXME: summarize #5880
Number Theory
- FIXME: summarize #5130
- FIXME: summarize #5822
- FIXME: summarize #5704
- FIXME: summarize #4193
- FIXME: summarize #5890
- FIXME: summarize #5856
Numerical
Packages
- FIXME: summarize #5803
- FIXME: summarize #5849
Move DSage to its own spkg (William Stein) -- The Distributed Sage framework (DSage) contained in sage/dsage is now packaged as a self-contained spkg. DSage allows for distributed computing from within Sage.
P-adics
- FIXME: summarize #5946
Quadratic Forms
Symbolics
Topology
User Interface
