|
Size: 987
Comment: Lay out general structure of release tour for Sage 3.4.2
|
Size: 13655
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 11: | Line 11: |
| * Comparison of ring coercion morphisms (Alex Ghitza) -- New comparison method {{{__cmp__()}}} for the class {{{RingHomomorphism_coercion}}} in {{{sage/rings/morphism.pyx}}}. The comparison method {{{__cmp__(self, other)}}} compares a ring coercion morphism {{{self}}} to {{{other}}}. Ring coercion morphisms never compare equal to any other data type. If {{{other}}} is a ring coercion morphism, the parents of {{{self}}} and {{{other}}} are compared. Here are some examples on comparing ring coercion morphisms: {{{ sage: f = ZZ.hom(QQ) sage: g = ZZ.hom(ZZ) sage: f == g False sage: f > g True sage: f < g False sage: h = Zmod(6).lift() sage: f == h False sage: f = ZZ.hom(QQ) sage: g = loads(dumps(f)) sage: f == g True }}} * FIXME: summarize #5921 * Coercing factors into a common universe (Alex Ghitza) -- New method {{{base_change(self, U)}}} in the module {{{sage/structure/factorization.py}}} to allow the factorization {{{self}}} with its factors (including the unit part) coerced into the universe {{{U}}}. Here's an example for working with the new method {{{base_change()}}}: {{{ sage: F = factor(2006) sage: F.universe() Integer Ring sage: P.<x> = ZZ["x"] sage: F.base_change(P).universe() Univariate Polynomial Ring in x over Integer Ring }}} |
|
| Line 17: | Line 51: |
| * Enhancements to symbolic logic (Chris Gorecki) -- This adds a number of utilities for working with symbolic logic: 1. {{{sage/logic/booleval.py}}} -- For evaluating boolean formulas. 1. {{{sage/logic/boolformula.py}}} -- For boolean evaluation of boolean formulas. 1. {{{sage/logic/logicparser.py}}} -- For creating and modifying parse trees of well-formed boolean formulas. 1. {{{sage/logic/logictable.py}}} -- For creating and printing truth tables associated with logical statements. 1. {{{sage/logic/propcalc.py}}} -- For propositional calculus. Here are some examples for working with the new symbolic logic modules: {{{ sage: import sage.logic.propcalc as propcalc sage: f = propcalc.formula("a&((b|c)^a->c)<->b") sage: g = propcalc.formula("boolean<->algebra") sage: (f&~g).ifthen(f) ((a&((b|c)^a->c)<->b)&(~(boolean<->algebra)))->(a&((b|c)^a->c)<->b) sage: f.truthtable() a b c value False False False True False False True True False True False False False True True False True False False True True False True False True True False True True True True True }}} * New function {{{squarefree_divisors()}}} (Robert Miller) -- The new function {{{squarefree_divisors(x)}}} in the module {{{sage/rings/arith.py}}} allows for iterating over the squarefree divisors (up to units) of the element {{{x}}}. Here, we assume that {{{x}}} is an element of any ring for which the function {{{prime_divisors()}}} works. Below are some examples for working with the new function {{{squarefree_divisors()}}}: {{{ sage: list(squarefree_divisors(7)) [1, 7] sage: list(squarefree_divisors(6)) [1, 2, 3, 6] sage: list(squarefree_divisors(81)) [1, 3] }}} |
|
| Line 29: | Line 101: |
| * Make {{{cartan_type}}} a method rather than an attribute (Dan Bump) -- For the module {{{sage/combinat/root_system/weyl_characters.py}}}, {{{cartan_type}}} is now a method, not an attribute. For example, one can now invoke {{{cartan_type}}} as a method like so: {{{ sage: A2 = WeylCharacterRing("A2") sage: A2([1,0,0]).cartan_type() ['A', 2] }}} |
|
| Line 32: | Line 112: |
| * Improved performance in {{{MPolynomialRing_libsingular}}} (Simon King) -- This provides some optimization of the method {{{MPolynomialRing_libsingular.__call__()}}}. In some cases, the efficiency is up to 19%. The following timing statistics are obtained using the machine sage.math: {{{ # BEFORE sage: R = PolynomialRing(QQ,5,"x") sage: S = PolynomialRing(QQ,6,"x") sage: T = PolynomialRing(QQ,5,"y") sage: U = PolynomialRing(GF(2),5,"x") sage: p = R("x0*x1+2*x4+x3*x1^2")^4 sage: timeit("q = S(p)") 625 loops, best of 3: 321 µs per loop sage: timeit("q = T(p)") 625 loops, best of 3: 348 µs per loop sage: timeit("q = U(p)") 625 loops, best of 3: 435 µs per loop # AFTER sage: R = PolynomialRing(QQ,5,"x") sage: S = PolynomialRing(QQ,6,"x") sage: T = PolynomialRing(QQ,5,"y") sage: U = PolynomialRing(GF(2),5,"x") sage: p = R("x0*x1+2*x4+x3*x1^2")^4 sage: timeit("q = S(p)") 625 loops, best of 3: 316 µs per loop sage: timeit("q = T(p)") 625 loops, best of 3: 281 µs per loop sage: timeit("q = U(p)") 625 loops, best of 3: 392 µs per loop }}} |
|
| Line 41: | Line 154: |
| * FIXME: summarize #5610 |
|
| Line 47: | Line 163: |
| * Default edge color is black (Robert Miller) -- If only one edge of a graph is colored red, for example, then the remaining edges should be colored with black by default. Here's an example: {{{ sage: G = graphs.CompleteGraph(5) sage: G.show(edge_colors={'red':[(0,1)]}) }}} {{attachment:pentagon-graph.png}} |
|
| Line 56: | Line 180: |
| * FIXME: summarize #5111 |
|
| Line 59: | Line 186: |
| * FIXME: summarize #5886 |
|
| Line 65: | Line 195: |
| * Vast speedup in {{{P1List}}} construction (John Cremona) -- This provides huge improvement in the {{{P1List()}}} constructor for Manin symbols. The efficiency gain can range from 27% up to 6x. Here are some timing statistics obtained using the machine sage.math: {{{ # BEFORE sage: time P1List(100000) CPU times: user 4.11 s, sys: 0.08 s, total: 4.19 s Wall time: 4.19 s The projective line over the integers modulo 100000 sage: time P1List(1000000) CPU times: user 192.22 s, sys: 0.60 s, total: 192.82 s Wall time: 192.84 s The projective line over the integers modulo 1000000 sage: time P1List(1009*1013) CPU times: user 31.20 s, sys: 0.05 s, total: 31.25 s Wall time: 31.25 s The projective line over the integers modulo 1022117 sage: time P1List(1000003) CPU times: user 35.92 s, sys: 0.05 s, total: 35.97 s Wall time: 35.97 s The projective line over the integers modulo 1000003 # AFTER sage: time P1List(100000) CPU times: user 0.78 s, sys: 0.02 s, total: 0.80 s Wall time: 0.80 s The projective line over the integers modulo 100000 sage: time P1List(1000000) CPU times: user 27.82 s, sys: 0.21 s, total: 28.03 s Wall time: 28.02 s The projective line over the integers modulo 1000000 sage: time P1List(1009*1013) CPU times: user 21.59 s, sys: 0.04 s, total: 21.63 s Wall time: 21.63 s The projective line over the integers modulo 1022117 sage: time P1List(1000003) CPU times: user 26.19 s, sys: 0.05 s, total: 26.24 s Wall time: 26.24 s The projective line over the integers modulo 1000003 }}} |
|
| Line 68: | Line 241: |
| * FIXME: summarize #5912 * Downloading and uploading folders of worksheets (Robert Bradshaw) -- One can now download and upload entire folders of worksheets at once, instead of individual worksheets one at a time. This also allows for downloading only selecting worksheets in one go. * FIXME: summarize #5880 |
|
| Line 71: | Line 253: |
| * Enhanced function {{{prime_pi()}}} for counting primes (R. Andrew Ohana) -- The improved function {{{prime_pi()}}} in {{{sage/functions/prime_pi.pyx}}} implements the prime counting function {{{pi(n)}}}. Essentially, {{{prime_pi(n)}}} counts the number of primes less than or equal to {{{n}}}. Here are some examples: {{{ sage: prime_pi(10) 4 sage: prime_pi(100) 25 sage: prime_pi(-10) 0 sage: prime_pi(-0.5) 0 sage: prime_pi(10^10) 455052511 }}} * Action of the Galois group on cusps (William Stein) -- New method {{{galois_action()}}} in {{{sage/modular/cusps.py}}} for computing action of the Galois group on cusps for congruence subgroups. The relevant algorithm here is taken from section 1.3 of the following text: * S. Glenn. Arithmetic on Modular Curves. Progress in Mathematics, volume 20, Birkhauser, 1982. Here are some examples for working with {{{galois_action()}}}: {{{ sage: Cusp(1/10).galois_action(3, 50) 1/170 sage: Cusp(oo).galois_action(3, 50) Infinity sage: Cusp(0).galois_action(3, 50) 0 }}} * Finding elliptic curves with prescribed reduction over {{{QQ}}} (John Cremona) -- New function {{{EllipticCurves_with_good_reduction_outside_S()}}} for constructing elliptic curves with good reduction outside a finite set of primes. This essentially implements the algorithm presented in the paper, but currently only over {{{QQ}}}: * J. Cremona and M. Lingham. Finding all elliptic curves with good reduction outside a given set of primes. Experimental Mathematics, 16(3):303--312, 2007. Here are some examples for working with this new function: {{{ sage: EllipticCurves_with_good_reduction_outside_S([]) [] sage: elist = EllipticCurves_with_good_reduction_outside_S([2]) sage: elist [Elliptic Curve defined by y^2 = x^3 + 4*x over Rational Field, Elliptic Curve defined by y^2 = x^3 - x over Rational Field, Elliptic Curve defined by y^2 = x^3 - 11*x - 14 over Rational Field, Elliptic Curve defined by y^2 = x^3 - 11*x + 14 over Rational Field, Elliptic Curve defined by y^2 = x^3 - 4*x over Rational Field, Elliptic Curve defined by y^2 = x^3 - 44*x - 112 over Rational Field, Elliptic Curve defined by y^2 = x^3 - 44*x + 112 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 + x + 1 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 - 9*x + 7 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 + 3*x - 5 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 - 2*x - 2 over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 + x - 1 over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 - 9*x - 7 over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 + 3*x + 5 over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 - 2*x + 2 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 - 3*x + 1 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 - 13*x - 21 over Rational Field, Elliptic Curve defined by y^2 = x^3 - 2*x over Rational Field, Elliptic Curve defined by y^2 = x^3 + 8*x over Rational Field, Elliptic Curve defined by y^2 = x^3 + 2*x over Rational Field, Elliptic Curve defined by y^2 = x^3 - 8*x over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 - 3*x - 1 over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 - 13*x + 21 over Rational Field] sage: len(elist) 24 sage: ', '.join([e.label() for e in elist]) '32a1, 32a2, 32a3, 32a4, 64a1, 64a2, 64a3, 64a4, 128a1, 128a2, 128b1, 128b2, 128c1, 128c2, 128d1, 128d2, 256a1, 256a2, 256b1, 256b2, 256c1, 256c2, 256d1, 256d2' }}} * Make elliptic curves over the mod rings {{{Z/pZ}}} behave like elliptic curves over the finite fields {{{GF(p)}}} (Alex Ghitza) -- Elliptic curves over {{{Z/NZ}}} for prime {{{N}}} are now treated as being over a finite field. For example, {{{ sage: F = Zmod(101) sage: EllipticCurve(F, [2, 3]) Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Ring of integers modulo 101 sage: E = EllipticCurve([F(2), F(3)]) sage: type(E) <class 'sage.schemes.elliptic_curves.ell_finite_field.EllipticCurve_finite_field'> }}} However, if {{{N}}} is composite, then elliptic curves over {{{Z/NZ}}} are treated as being of the type "generic elliptic curve". For example, {{{ sage: F = Zmod(95) sage: EllipticCurve(F, [2, 3]) Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Ring of integers modulo 95 sage: E = EllipticCurve([F(2), F(3)]) sage: type(E) <class 'sage.schemes.elliptic_curves.ell_generic.EllipticCurve_generic'> }}} * FIXME: summarize #5890 |
|
| Line 77: | Line 350: |
| * Upgrade [[http://www.cython.org|Cython]] to version 0.11.1 latest upstream release (Robert Bradshaw) -- Based on Pyrex, Cython is a language that closely resembles Python and developed for writing C extensions for Python. For critical functionalities and performance, Sage uses Cython to generate very efficient C code from Cython code, for wrapping external C libraries, and for fast C modules that speed up the execution of Python code. * Upgrade [[http://www.mpir.org|MPIR|]] to version 1.1.1 latest upstream release (Michael Abshoff) -- MPIR is a library for multiprecision integers and rationals based on the [[http://www.gmplib.org|GMP project]]. Among other things, MPIR aims to provide native build capability under Windows. * Move DSage to its own spkg (William Stein) -- The Distributed Sage framework (DSage) contained in {{{sage/dsage}}} is now packaged as a self-contained spkg. DSage allows for distributed computing from within Sage. * Update the FLINT spkg (Michael Abshoff) -- The new FLINT spkg is {{{flint-1.2.4.p2.spkg}}} and fixes spkg-check on OS X 64-bit. == P-adics == * FIXME: summarize #5946 |
Sage 3.4.2 Release Tour
Sage 3.4.2 was released on FIXME. For the official, comprehensive release note, please refer to sage-3.4.2.txt. A nicely formatted version of this release tour can be found at FIXME. The following points are some of the foci of this release:
Algebra
Comparison of ring coercion morphisms (Alex Ghitza) -- New comparison method __cmp__() for the class RingHomomorphism_coercion in sage/rings/morphism.pyx. The comparison method __cmp__(self, other) compares a ring coercion morphism self to other. Ring coercion morphisms never compare equal to any other data type. If other is a ring coercion morphism, the parents of self and other are compared. Here are some examples on comparing ring coercion morphisms:
sage: f = ZZ.hom(QQ) sage: g = ZZ.hom(ZZ) sage: f == g False sage: f > g True sage: f < g False sage: h = Zmod(6).lift() sage: f == h False sage: f = ZZ.hom(QQ) sage: g = loads(dumps(f)) sage: f == g True
- FIXME: summarize #5921
Coercing factors into a common universe (Alex Ghitza) -- New method base_change(self, U) in the module sage/structure/factorization.py to allow the factorization self with its factors (including the unit part) coerced into the universe U. Here's an example for working with the new method base_change():
sage: F = factor(2006) sage: F.universe() Integer Ring sage: P.<x> = ZZ["x"] sage: F.base_change(P).universe() Univariate Polynomial Ring in x over Integer Ring
Algebraic Geometry
Basic Arithmetic
- Enhancements to symbolic logic (Chris Gorecki) -- This adds a number of utilities for working with symbolic logic:
sage/logic/booleval.py -- For evaluating boolean formulas.
sage/logic/boolformula.py -- For boolean evaluation of boolean formulas.
sage/logic/logicparser.py -- For creating and modifying parse trees of well-formed boolean formulas.
sage/logic/logictable.py -- For creating and printing truth tables associated with logical statements.
sage/logic/propcalc.py -- For propositional calculus.
sage: import sage.logic.propcalc as propcalc sage: f = propcalc.formula("a&((b|c)^a->c)<->b") sage: g = propcalc.formula("boolean<->algebra") sage: (f&~g).ifthen(f) ((a&((b|c)^a->c)<->b)&(~(boolean<->algebra)))->(a&((b|c)^a->c)<->b) sage: f.truthtable() a b c value False False False True False False True True False True False False False True True False True False False True True False True False True True False True True True True True New function squarefree_divisors() (Robert Miller) -- The new function squarefree_divisors(x) in the module sage/rings/arith.py allows for iterating over the squarefree divisors (up to units) of the element x. Here, we assume that x is an element of any ring for which the function prime_divisors() works. Below are some examples for working with the new function squarefree_divisors():
sage: list(squarefree_divisors(7)) [1, 7] sage: list(squarefree_divisors(6)) [1, 2, 3, 6] sage: list(squarefree_divisors(81)) [1, 3]
Build
Calculus
Coercion
Combinatorics
Make cartan_type a method rather than an attribute (Dan Bump) -- For the module sage/combinat/root_system/weyl_characters.py, cartan_type is now a method, not an attribute. For example, one can now invoke cartan_type as a method like so:
sage: A2 = WeylCharacterRing("A2") sage: A2([1,0,0]).cartan_type() ['A', 2]
Commutative Algebra
Improved performance in MPolynomialRing_libsingular (Simon King) -- This provides some optimization of the method MPolynomialRing_libsingular.__call__(). In some cases, the efficiency is up to 19%. The following timing statistics are obtained using the machine sage.math:
# BEFORE sage: R = PolynomialRing(QQ,5,"x") sage: S = PolynomialRing(QQ,6,"x") sage: T = PolynomialRing(QQ,5,"y") sage: U = PolynomialRing(GF(2),5,"x") sage: p = R("x0*x1+2*x4+x3*x1^2")^4 sage: timeit("q = S(p)") 625 loops, best of 3: 321 µs per loop sage: timeit("q = T(p)") 625 loops, best of 3: 348 µs per loop sage: timeit("q = U(p)") 625 loops, best of 3: 435 µs per loop # AFTER sage: R = PolynomialRing(QQ,5,"x") sage: S = PolynomialRing(QQ,6,"x") sage: T = PolynomialRing(QQ,5,"y") sage: U = PolynomialRing(GF(2),5,"x") sage: p = R("x0*x1+2*x4+x3*x1^2")^4 sage: timeit("q = S(p)") 625 loops, best of 3: 316 µs per loop sage: timeit("q = T(p)") 625 loops, best of 3: 281 µs per loop sage: timeit("q = U(p)") 625 loops, best of 3: 392 µs per loop
Distribution
Doctest
Documentation
- FIXME: summarize #5610
Geometry
Graph Theory
- Default edge color is black (Robert Miller) -- If only one edge of a graph is colored red, for example, then the remaining edges should be colored with black by default. Here's an example:
sage: G = graphs.CompleteGraph(5) sage: G.show(edge_colors={'red':[(0,1)]})
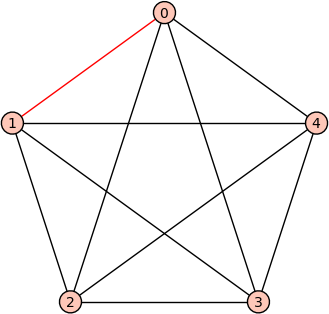
Graphics
Group Theory
Interfaces
- FIXME: summarize #5111
Linear Algebra
- FIXME: summarize #5886
Miscellaneous
Modular Forms
Vast speedup in P1List construction (John Cremona) -- This provides huge improvement in the P1List() constructor for Manin symbols. The efficiency gain can range from 27% up to 6x. Here are some timing statistics obtained using the machine sage.math:
# BEFORE sage: time P1List(100000) CPU times: user 4.11 s, sys: 0.08 s, total: 4.19 s Wall time: 4.19 s The projective line over the integers modulo 100000 sage: time P1List(1000000) CPU times: user 192.22 s, sys: 0.60 s, total: 192.82 s Wall time: 192.84 s The projective line over the integers modulo 1000000 sage: time P1List(1009*1013) CPU times: user 31.20 s, sys: 0.05 s, total: 31.25 s Wall time: 31.25 s The projective line over the integers modulo 1022117 sage: time P1List(1000003) CPU times: user 35.92 s, sys: 0.05 s, total: 35.97 s Wall time: 35.97 s The projective line over the integers modulo 1000003 # AFTER sage: time P1List(100000) CPU times: user 0.78 s, sys: 0.02 s, total: 0.80 s Wall time: 0.80 s The projective line over the integers modulo 100000 sage: time P1List(1000000) CPU times: user 27.82 s, sys: 0.21 s, total: 28.03 s Wall time: 28.02 s The projective line over the integers modulo 1000000 sage: time P1List(1009*1013) CPU times: user 21.59 s, sys: 0.04 s, total: 21.63 s Wall time: 21.63 s The projective line over the integers modulo 1022117 sage: time P1List(1000003) CPU times: user 26.19 s, sys: 0.05 s, total: 26.24 s Wall time: 26.24 s The projective line over the integers modulo 1000003
Notebook
- FIXME: summarize #5912
- Downloading and uploading folders of worksheets (Robert Bradshaw) -- One can now download and upload entire folders of worksheets at once, instead of individual worksheets one at a time. This also allows for downloading only selecting worksheets in one go.
- FIXME: summarize #5880
Number Theory
Enhanced function prime_pi() for counting primes (R. Andrew Ohana) -- The improved function prime_pi() in sage/functions/prime_pi.pyx implements the prime counting function pi(n). Essentially, prime_pi(n) counts the number of primes less than or equal to n. Here are some examples:
sage: prime_pi(10) 4 sage: prime_pi(100) 25 sage: prime_pi(-10) 0 sage: prime_pi(-0.5) 0 sage: prime_pi(10^10) 455052511
Action of the Galois group on cusps (William Stein) -- New method galois_action() in sage/modular/cusps.py for computing action of the Galois group on cusps for congruence subgroups. The relevant algorithm here is taken from section 1.3 of the following text:
- S. Glenn. Arithmetic on Modular Curves. Progress in Mathematics, volume 20, Birkhauser, 1982.
Here are some examples for working with galois_action():
sage: Cusp(1/10).galois_action(3, 50) 1/170 sage: Cusp(oo).galois_action(3, 50) Infinity sage: Cusp(0).galois_action(3, 50) 0
Finding elliptic curves with prescribed reduction over QQ (John Cremona) -- New function EllipticCurves_with_good_reduction_outside_S() for constructing elliptic curves with good reduction outside a finite set of primes. This essentially implements the algorithm presented in the paper, but currently only over QQ:
- J. Cremona and M. Lingham. Finding all elliptic curves with good reduction outside a given set of primes. Experimental Mathematics, 16(3):303--312, 2007.
sage: EllipticCurves_with_good_reduction_outside_S([]) [] sage: elist = EllipticCurves_with_good_reduction_outside_S([2]) sage: elist [Elliptic Curve defined by y^2 = x^3 + 4*x over Rational Field, Elliptic Curve defined by y^2 = x^3 - x over Rational Field, Elliptic Curve defined by y^2 = x^3 - 11*x - 14 over Rational Field, Elliptic Curve defined by y^2 = x^3 - 11*x + 14 over Rational Field, Elliptic Curve defined by y^2 = x^3 - 4*x over Rational Field, Elliptic Curve defined by y^2 = x^3 - 44*x - 112 over Rational Field, Elliptic Curve defined by y^2 = x^3 - 44*x + 112 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 + x + 1 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 - 9*x + 7 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 + 3*x - 5 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 - 2*x - 2 over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 + x - 1 over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 - 9*x - 7 over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 + 3*x + 5 over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 - 2*x + 2 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 - 3*x + 1 over Rational Field, Elliptic Curve defined by y^2 = x^3 + x^2 - 13*x - 21 over Rational Field, Elliptic Curve defined by y^2 = x^3 - 2*x over Rational Field, Elliptic Curve defined by y^2 = x^3 + 8*x over Rational Field, Elliptic Curve defined by y^2 = x^3 + 2*x over Rational Field, Elliptic Curve defined by y^2 = x^3 - 8*x over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 - 3*x - 1 over Rational Field, Elliptic Curve defined by y^2 = x^3 - x^2 - 13*x + 21 over Rational Field] sage: len(elist) 24 sage: ', '.join([e.label() for e in elist]) '32a1, 32a2, 32a3, 32a4, 64a1, 64a2, 64a3, 64a4, 128a1, 128a2, 128b1, 128b2, 128c1, 128c2, 128d1, 128d2, 256a1, 256a2, 256b1, 256b2, 256c1, 256c2, 256d1, 256d2'
Make elliptic curves over the mod rings Z/pZ behave like elliptic curves over the finite fields GF(p) (Alex Ghitza) -- Elliptic curves over Z/NZ for prime N are now treated as being over a finite field. For example,
sage: F = Zmod(101) sage: EllipticCurve(F, [2, 3]) Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Ring of integers modulo 101 sage: E = EllipticCurve([F(2), F(3)]) sage: type(E) <class 'sage.schemes.elliptic_curves.ell_finite_field.EllipticCurve_finite_field'>
However, if N is composite, then elliptic curves over Z/NZ are treated as being of the type "generic elliptic curve". For example,
sage: F = Zmod(95) sage: EllipticCurve(F, [2, 3]) Elliptic Curve defined by y^2 = x^3 + 2*x + 3 over Ring of integers modulo 95 sage: E = EllipticCurve([F(2), F(3)]) sage: type(E) <class 'sage.schemes.elliptic_curves.ell_generic.EllipticCurve_generic'>
- FIXME: summarize #5890
Numerical
Packages
Upgrade Cython to version 0.11.1 latest upstream release (Robert Bradshaw) -- Based on Pyrex, Cython is a language that closely resembles Python and developed for writing C extensions for Python. For critical functionalities and performance, Sage uses Cython to generate very efficient C code from Cython code, for wrapping external C libraries, and for fast C modules that speed up the execution of Python code.
Upgrade MPIR to version 1.1.1 latest upstream release (Michael Abshoff) -- MPIR is a library for multiprecision integers and rationals based on the GMP project. Among other things, MPIR aims to provide native build capability under Windows.
Move DSage to its own spkg (William Stein) -- The Distributed Sage framework (DSage) contained in sage/dsage is now packaged as a self-contained spkg. DSage allows for distributed computing from within Sage.
Update the FLINT spkg (Michael Abshoff) -- The new FLINT spkg is flint-1.2.4.p2.spkg and fixes spkg-check on OS X 64-bit.
P-adics
- FIXME: summarize #5946
Quadratic Forms
Symbolics
Topology
User Interface
